Hoofdstuk 6
Energie
§1 Soorten energie §2 Energiebehoud §3 Chemische energie
§1 Soorten energie
In dit hoofdstuk gaan we leren de beweging van voorwerpen te beschrijven met behulp van het begrip energie. In de eerste paragraaf introduceren we een aantal soorten energie en de bijbehorende formules en gaan we het hebben over energieomzettingen.
Als we een stukje willen rennen, dan hebben we daar energie voor nodig. Als een vliegtuig opstijgt, dan is daar energie voor nodig. Als een lamp licht geeft, dan verbruikt deze lamp energie. Energie is overal om ons heen. Er zijn verschillende soorten energie. Als een voorwerp beweegt, dan zeggen we dat het voorwerp kinetische energie (Ekin) heeft. De hoeveelheid kinetische energie die een bewegend voorwerp heeft, kunnen we berekenen met de volgende formule:
$$ E_{kin} = \frac{1}{2}mv^2 $$
|
Voor alle formules in deze paragraaf geldt dat je de grootheden moet invullen in SI-eenheden. De massa in deze formule wil je altijd in kilogram geven en de snelheid in meter per seconde. De SI-eenheid van de energie is de joule.
Voorbeeld
|
|
Vraag: Een leerling fietst met een bewegingsenergie van 1,0 × 104 J. De leerling heeft samen met de fiets een massa van 90 kg. Bereken de snelheid waarmee de leerling fietst. Antwoord: Eerst noteren we de gegevens: Ekin = 1,0 × 104 J m = 90 kg We gebruiken de formule voor de bewegingsenergie: $$ E_{kin} = \frac{1}{2}mv^2 $$Nu vullen we de gegevens zo veel mogelijk in: $$ 1,0 \times 10^4 = \frac{1}{2} \times 90 \times v^2 $$Door 1/2 × 90 uit te rekenen vinden we: $$ 1,0 \times 10^4 = 45 \times v^2 $$Dit schrijven we om tot: $$ v^2 = \frac{1,0 \times 10^4}{45} = 222,22 $$Door aan beide kanten de wortel te trekken vinden we de snelheid: $$ v = \sqrt{222,22} = 14,9 \text{ m/s} $$
|
Ook heeft een voorwerp energie als het de potentie heeft zichzelf of een ander voorwerp in beweging te brengen. Een voorbeeld is de zwaarte-energie. Als je een zwaar voorwerp optilt, dan voel je dat het weer naar beneden wil. Dit is de zwaarte-energie. Elk voorwerp dat zich op een bepaalde hoogte bevindt, heeft dus zwaarte-energie. De hoeveelheid zwaarte-energie berekenen we als volgt:
$$ E_z = mgh $$
|
|
EXPERIMENT
| ||
|
Een ander voorbeeld is de veerenergie of de elastische energie. Als je een veer of een elastiek uitrekt, dan voel je dat deze voorwerpen terug willen naam hun evenwichtspositie. We zeggen dan dat deze voorwerpen veerenergie of elastische energie bevatten.
Chemische energie (Ech) is de energie die is opgeslagen in stoffen. Een bekend voorbeeld is de energie die in brandstoffen als benzine is opgeslagen. Chemische energie zit ook in bijvoorbeeld voedsel en batterijen.
Daarnaast hebben we ook elektrische energie (Eelek) en stralingsenergie (Estraling). Met stralingsenergie bedoelen we de energie in licht. We voelen deze energie bijvoorbeeld als we in de zon lopen.
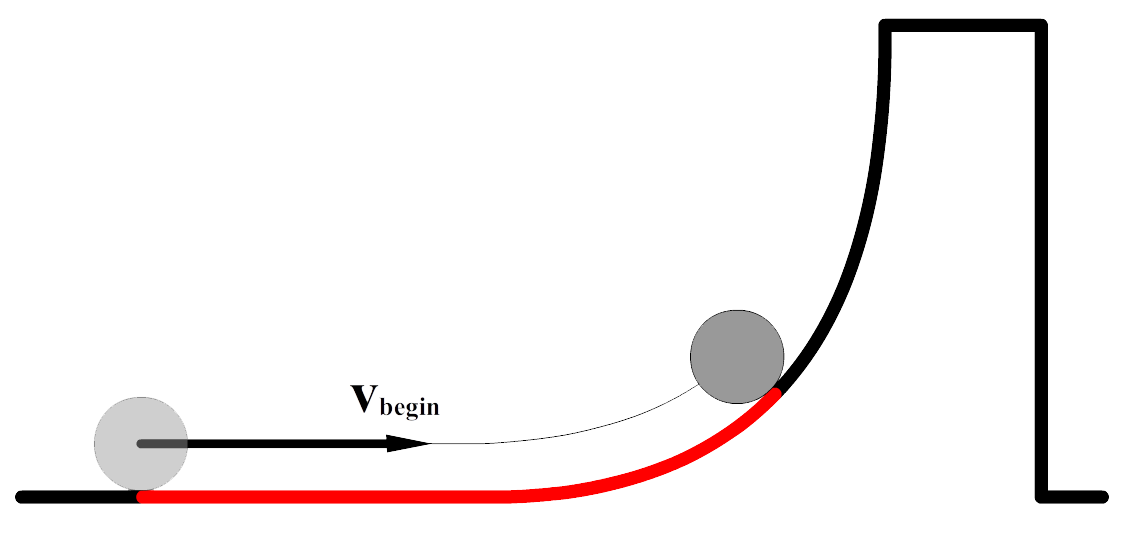
Door wrijvingskracht ontstaat de energiesoort warmte (Q). Dat wrijving voor warmte zorgt kan je o.a. ervaren door je handen hard tegen elkaar aan te wrijven. We zien hetzelfde effect in de onderstaande foto die is gemaakt met een infraroodcamera. We zien hier dat de grond is opgewarmd door het remmen van een fiets.
|
EXPERIMENT
| ||
|
De warmte berekenen we als volgt:
$$ Q = F_w \;s $$
|
De verschillende soorten energie kunnen in elkaar worden omgezet. Neem bijvoorbeeld de verbranding van voedsel in het lichaam. Hier wordt de chemische energie uit voedsel omgezet in kinetische energie en warmte. Deze energieomzetting schrijven we als volgt op:
$$ E_{ch} \rightarrow E_{kin} + Q $$Nog een voorbeeld. Als we een lampje aansluiten op een batterij, dan wordt in de batterij chemische energie omgezet in elektrische energie en warmte. In de lamp wordt deze elektrische energie op zijn beurt weer omgezet in stralingsenergie en warmte. Deze energieomzettingen schrijven we als volgt op:
$$ E_{ch} \rightarrow E_{elek} + Q $$ $$ E_{elek} \rightarrow E_{straling} + Q $$
INSTRUCTIE:
Soorten energie
|
Leerdoelen:
|
|
|
Opdrachten
|
|
§2 Energiebehoud
In deze paragraaf bouwen we voort op de soorten energie die we in de vorige paragraaf tegen zijn gekomen. We gaan het begrip energiebehoud gebruiken om met deze soorten energie te rekenen.
Zoals we hebben gelezen kunnen we energie omzetten van de ene naar de andere soort, maar de totale hoeveelheid energie blijft altijd gelijk. We noemen dit de wet van behoud van energie. In wiskundige termen kunnen we deze wet opschrijven als:
$$ E_{tot,b} = E_{tot,e} $$
|
|
EXPERIMENT
|
|
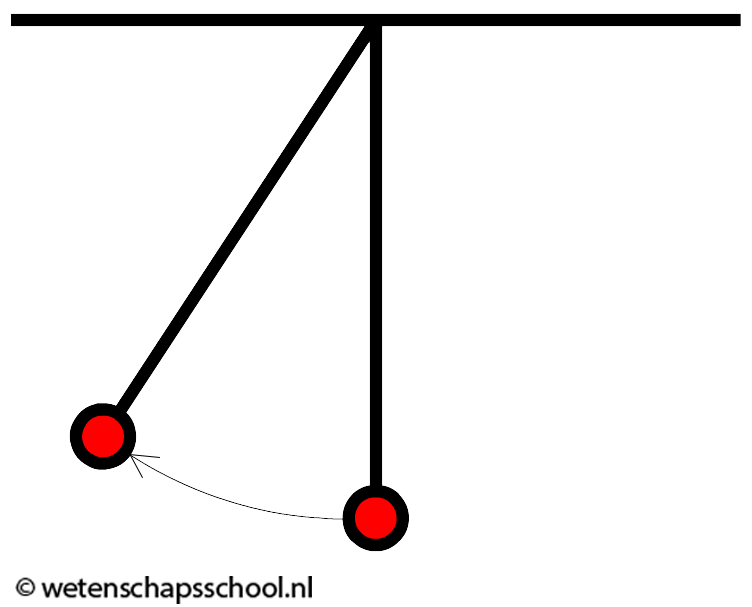
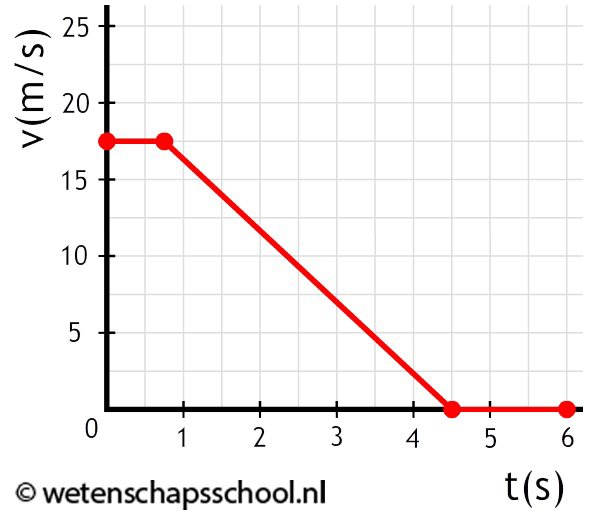
In de onderstaande filmpjes wordt de wet van behoud van energie gedemonstreerd:
DEMO-VIDEO:
Energiebehoud
DEMO-VIDEO:
Energiebehoud II
|
In de onderstaande voorbeelden gaan we deze wet toepassen.
|
Voorbeeld
|
|
Opdracht: Een kanonskogel met onbekende massa wordt onder een willekeurige hoek afgeschoten van de top van een kasteel op een hoogte van 30 m. De beginsnelheid van de kogel is 20 m/s. Bereken de snelheid waarmee de kogel tegen de grond komt. We verwaarlozen de wrijvingskracht.
Antwoord: Op het moment dat de kogel wordt afgeschoten heeft de kogel zowel kinetische energie als zwaarte-energie. Als de kogel neerkomt, is er geen zwaarte-energie meer. Er geldt dus: $$ E_{tot,b} = E_{tot,e} $$ $$ E_{kin,b} + E_{z,b} = E_{kin,e} $$Dit kunnen we uitschrijven tot: $$ \frac{1}{2}mv_{b}^2 + mgh = \frac{1}{2}mv_{e}^2 $$Alle termen in deze vergelijking bevatten een m, dus kunnen we deze wegdelen: $$ \frac{1}{2}v_{b}^2 + gh = \frac{1}{2}v_{e}^2 $$Laten we nu de gegevens die we gekregen hebben invullen: $$ \frac{1}{2}\times 20^2 + 9,81 \times 30 = \frac{1}{2}v_{e}^2 $$De linker zijde kunnen we nu versimpelen tot: $$ 494,3 = \frac{1}{2}v_{e}^2 $$De 1/2 aan de rechter zijde kunnen we wegkrijgen door beide kanten van de vergelijking met 2 te vermenigvuldigen: $$ 988,6 = v_{e}^2 $$Als we nu aan beide kanten de wortel trekken, dan vinden we de eindsnelheid: $$ v_{e} = \sqrt{988,6} = 31 \text{ m/s} $$Merk op hoe krachtig deze methode is! Met energiebehoud kunnen we de eindsnelheid van de kogel berekenen, zonder de massa van de kogel te weten of de hoek waaronder de kogel is afgeschoten.
|
Laten we nu een voorbeeld bespreken waarbij de wrijvingskracht wel een rol speelt:
|
Voorbeeld
|
|
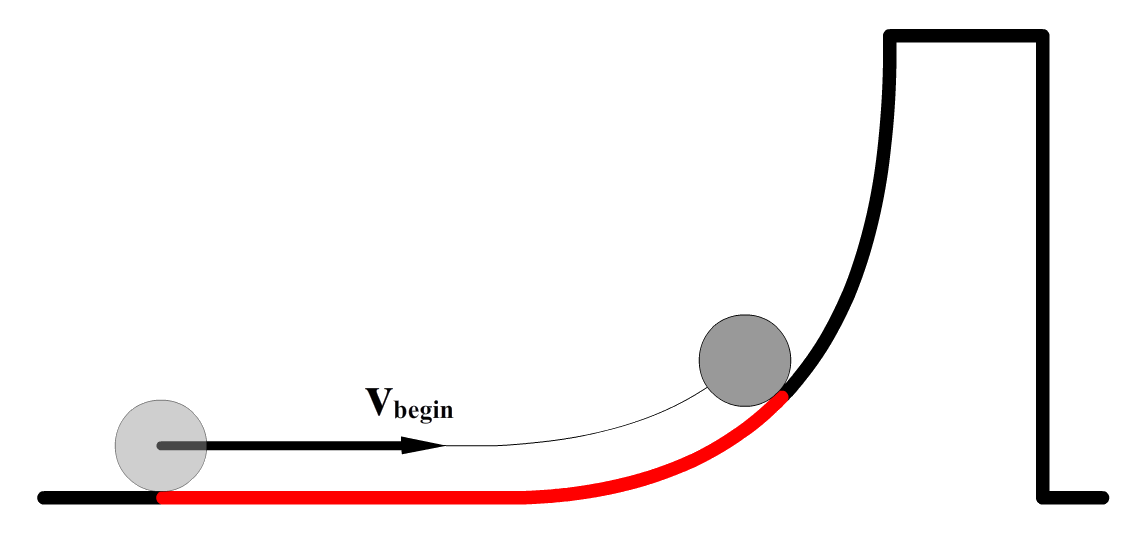
Opdracht: Een bal met een massa van 1,0 kg wordt met een snelheid van 5 m/s tegen een helling opgerold. Op een hoogte van 10 cm staat de bal even stil. Op dit punt heeft de bal 1,5 meter afgelegd. Bereken de gemiddelde wrijvingskracht die werkt op de bal.
Antwoord: Aan het begin heeft de bal kinetische energie, want de bal heeft aan het begin een snelheid. Op zijn hoogste punt heeft de bal geen kinetische energie meer, want de bal staat hier even stil. De bal heeft hier wel zwaarte-energie. Er geldt dus: $$ E_{tot,b} = E_{tot,e} $$ $$ E_{kin,b} = E_{z,e} + Q $$Dit kunnen we uitschrijven tot: $$ \frac{1}{2}mv_b^2 = mgh + F_w \;s $$Omdat de laatste term geen "m" bevat, kunnen we deze niet wegdelen. Nu vullen we de gegevens in: $$ \frac{1}{2} 1,0 \times 5^2 = 1,0 \times 9,81 \times 0,10 + F_w \times 1,5 $$ $$ 12,5 = 0,981 + F_w \times 1,5 $$Als we aan beide kanten 0,981 van de vergelijking afhalen, dan vinden we: $$ 11,519 = F_w \times 1,5 $$Hiermee kunnen we de wrijvingskracht uitrekenen: $$ F_w = \frac{11,519}{1,5} = 7,7 \text{ N} $$
|
INSTRUCTIE:
Energiebehoud
|
Leerdoelen:
|
|
|
Opdrachten
|
|
§3 Chemische energie
In de eerste paragraaf hebben we het gehad over chemische energie. Dit is de energie die is opgeslagen in de bindingen tussen atomen. Een bekend voorbeeld is de energie in brandstoffen zoals benzine. In deze paragraaf gaan we met deze energie leren rekenen. Ook gaan we het kort hebben over energiecentrales.
In verbrandingsmotoren wordt de chemische energie in brandstof gebruikt om arbeid (W) te verrichten (over dit begrip leren we meer in de 5de klas). Deze arbeid kan dan bijvoorbeeld gebruikt worden om een auto in beweging te brengen (in dat geval zorgt de arbeid voor een omzetting van chemische energie naar kinetische energie) of je gebruikt een motor bijvoorbeeld om iets op te tillen (in dat geval wordt de chemische energie omgezet in zwaarte-energie). Niet alle chemische energie in de motor zal echter nuttig gebruikt worden. Er gaat namelijk ook veel energie verloren in de vorm van warmte (Q). Er geldt dus:
$$ E_{ch} = W + Q $$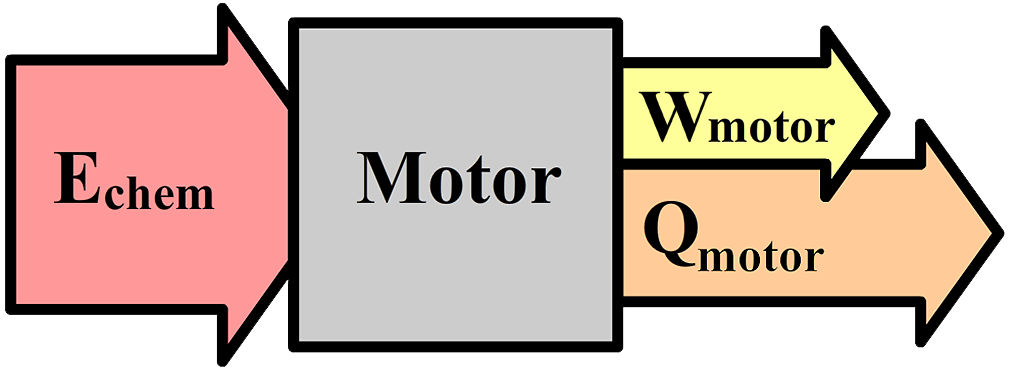
De fractie van de energie die nuttig gebruikt wordt noemen we het rendement:
$$ \frac{E_{nuttig}}{E_{totaal}} = \eta $$
|
Het rendement is in deze formule een getal tussen de 0 en de 1. Het rendement wordt ook vaak uitgedrukt als percentage. In dat geval moet het rendement uit de formule vermenigvuldigd worden met 100. Als η = 0,20, dan is het rendement dus 20%. Als η = 0,02, dan is het rendement dus 2%.
In het geval van een verbrandingsmotor kunnen we de formule herschrijven tot:
$$ \frac{W_{m}}{E_{ch}} = \eta $$
|
We kunnen de arbeid die de motor verricht ook uitrekenen met de volgende formule:
$$ W_{motor} = F_{motor} \; s $$
|
De chemische energie berekenen we met de stookwaarde (rV). De stookwaarde vertelt ons hoeveel joule aan chemische energie er in een kubieke meter van een bepaalde brandstof zit. Benzine heeft bijvoorbeeld een stookwaarde van 33 × 109 J/m3. Dit betekent dus dat je uit een kubieke meter benzine 33 × 109 joule aan chemische energie kan halen. Voor een heel aantal brandstoffen kan je de stookwaarde in BINAS opzoeken. Met de stookwaarde kunnen we als volgt de hoeveelheid chemische energie berekenen:
$$ E_{ch} = r_v V$$
|
Ook in voedsel zit energie. Voor pinda's is de stookwaarde bijvoorbeeld ongeveer de 24 × 106 J/kg. Een enkele pinda kan je hier bijna twee minuten op laten branden (zie het onderstaande filmpje)!
|
EXPERIMENT
| ||
|
|
Voorbeeld
|
|
Opdracht: Een verbrandingsmotor levert 10 × 107 J aan nuttige energie en heeft een rendement van 30%. Bereken hoeveel liter benzine hiervoor moet worden verbrand. Antwoord: Laten we eerst de gegevens opschrijven: In BINAS vinden we: rbenzine = 33 × 109 J/m3 Dan gebruiken we de formule voor het rendement: $$ \frac{W_m}{E_{ch}} = \eta $$Hiermee berekenen we de chemische energie: $$ E_{ch} = \frac{W_m}{\eta} = \frac{10 \times 10^7}{0,30} = 3,3 \times 10^{8} \text{ J} $$Met de chemische energie berekenen we het volume: $$ V = \frac{E_{ch}}{r_V} = \frac{3,3 \times 10^{8} }{33\times 10^9} = 0,010 \text{ m}^3 = 10 \text{ L}$$Er is dus 10 L benzine verbrand.
|
Veel van de energie die we in huishoudens gebruiken komt van energiecentrales. In de volgende afbeelding zien we een traditionele fossiele brandstofcentrale. In de centrale die is afgebeeld wordt het (behoorlijk vervuilende) steenkool als brandstof gebruikt, maar hetzelfde systeem kan ook gebruikt worden voor andere fossiele brandstoffen zoals aardgas. De steenkool wordt uit een mijn gehaald en verbrand in een oven, Met de warmte die hierbij vrijkomt, wordt water aan de kook gebracht. De stoom die hierbij ontstaat, zorgt dat een turbine gaat draaien. De turbine zorgt op zijn beurt voor het draaien van spoelen in een generator. Door spoelen te laten bewegen in de buurt van magneten, wordt hiermee elektriciteit opgewekt.
Een soortgelijk systeem gebruiken we voor het opwekken van elektrische energie uit schonere energiebronnen. Denk bijvoorbeeld aan een waterkrachtcentrale, een windmolen, en een kerncentrale. Bij een windmolen wordt de turbine aangedreven door wind en bij een waterkrachtcentrale met behulp van water. Bij een kerncentrale wordt energie opgewekt door het splijten van zware atoomkernen zoals uranium. De warmte die bij een kernreactor vrijkomt, wordt net als bij de kolencentrale gebruikt om water aan de kook te brengen en zo met de ontstane stoom een turbine te laten draaien.
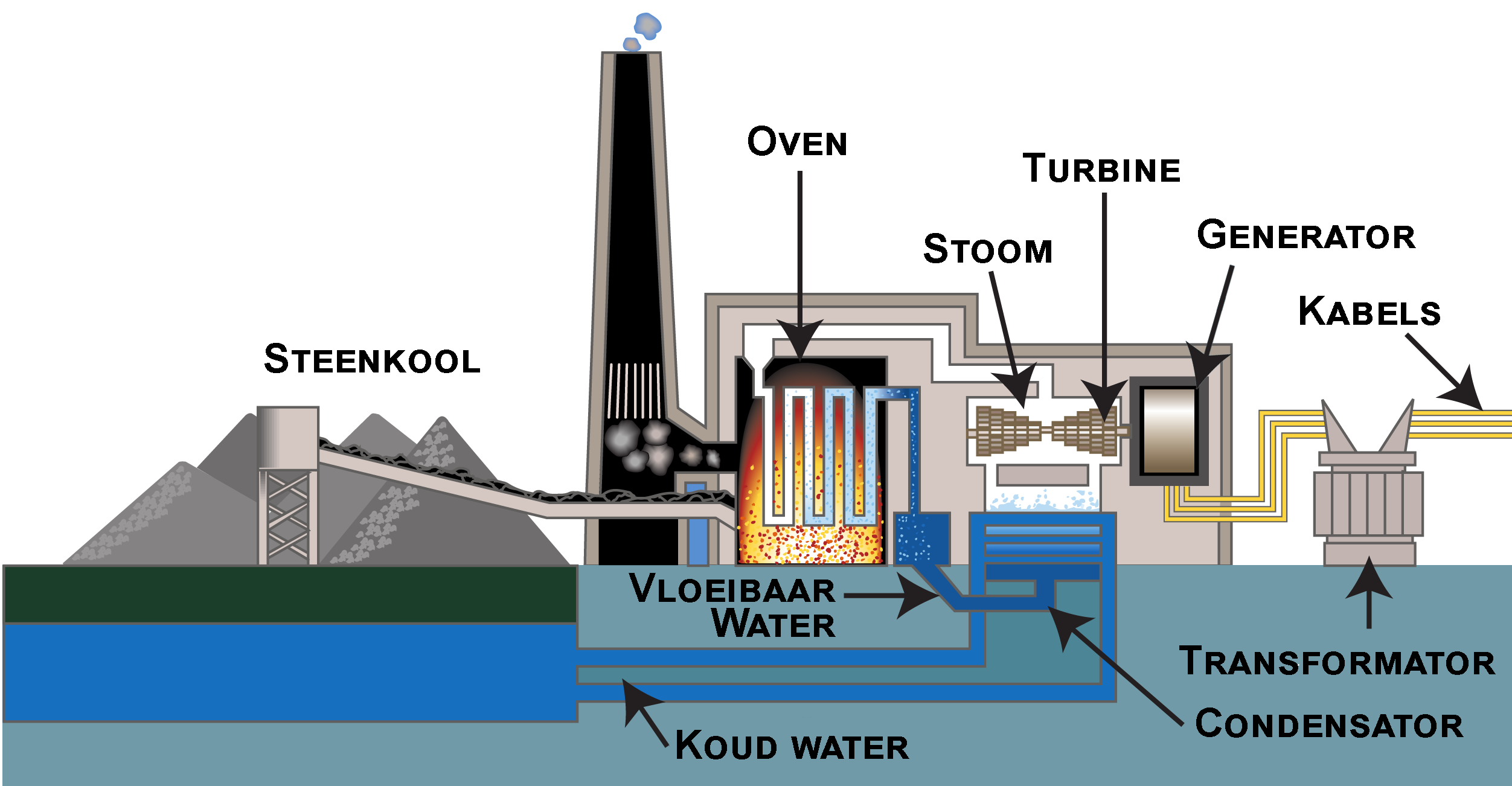(Afbeelding: Tennessee Valley Authority; PD)
Hieronder zien we het energie-stroomdiagram behorende bij een fossiele brandstofcentrale. De energiebron is hier de chemische energie in de fossiele brandstof, de turbine zet dit om in kinetische energie en de generator zet deze energie weer om in elektrische energie. Bij beide omzettingen komt ook warmte (Q) vrij. Dit gaat verloren.
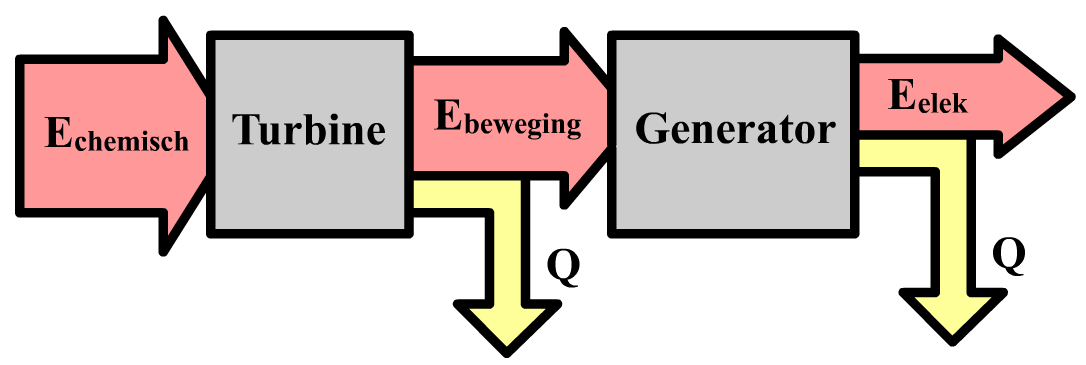
Hieronder zien we het energie-stroomdiagram van windenergie. Bij windenergie wordt kinetische energie van lucht met een generator omgezet in elektriciteit en warmte:
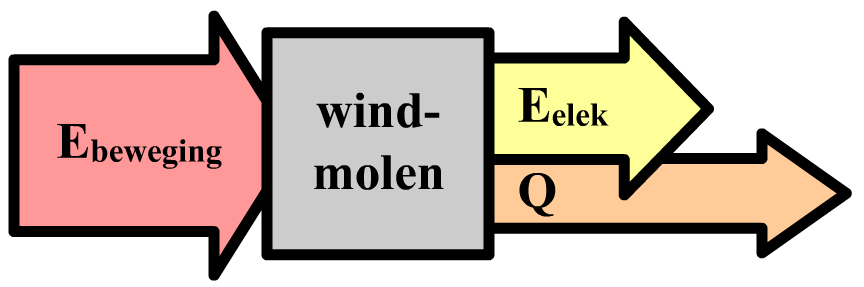
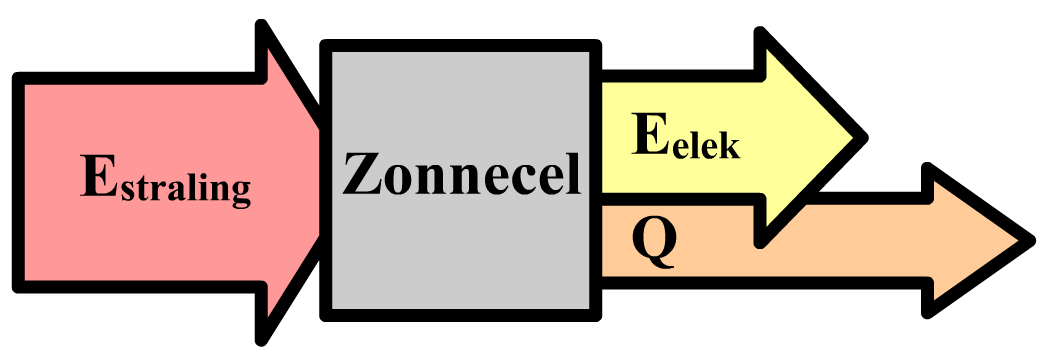
Tegenwoordig worden veel huishoudens ook van energie voorzien met behulp van zonnecellen. Zonnecellen bestaan uit zogenaamde halfgeleiders die als eigenschap hebben dat ze elektriciteit genereren als er licht op valt. Hieronder zien we het bijbehorende energie-stroomdiagram:
INSTRUCTIE:
Chemische energie
|
Leerdoelen:
|
|
|
Opdrachten
|
|
| BINAS: | |
| 28B | Stookwaarden |