BASIS

BEWEGING

KRACHT

ELEKTRICITEIT

antwoorden

antwoorden

antwoorden

antwoorden

videolessen

videolessen

videolessen

videolessen

oefentoets

oefentoets

oefentoets

oefentoets

MECHANICA

ENERGIE

MOMENT

MODELLEREN

videolessen

videolessen

videolessen

videolessen

antwoorden

antwoorden

antwoorden

antwoorden

oefentoets

oefentoets

oefentoets

oefentoets

RADIOACTIVITEIT (UIT VMBO BOEK)

...

...

...

Hoofdstuk 5
Mechanica

§1 Significante cijfers
§2 Eenheden afleiden
§3 De raaklijn
§4 De tweede wet van Newton

§1     Significante cijfers

In dit hoofdstuk gaan we nogmaals kijken naar de onderwerpen beweging en kracht. Voordat we dit gaan doen, gaan we eerst een meer professionele manier aanleren om natuurkunde te bedrijven. In deze paragraaf gaan we bestuderen hoe we in de natuurkunde afronden. Dit doen we met behulp van significante cijfers.

In de natuurkunde werken we met metingen en metingen zijn vaak onnauwkeurig. Het ligt daarom voor de hand dat we cijfers in de natuurkunde afronden op basis van de nauwkeurigheid van de meting. Hoe nauwkeuriger de meting is, op hoe meer getallen we de meetwaarde afronden.

Neem bijvoorbeeld het potlood in de volgende afbeelding. De meeste mensen zullen waarschijnlijk zeggen dat dit potlood een lengte van 11 cm heeft. We kunnen de lengte van het potlood echter nauwkeurig genoeg aflezen, dat we zeker weten dat het eerste getal achter de komma een nul moet zijn. We zeggen daarom dat de lengte van dit potlood 11,0 cm is. We zien hier dus dat bij natuurkunde de nullen achter de komma van belang zijn!

De cijfers waarin we een meetwaarde mogen noteren noemen we significante cijfers. De meetwaarde 11,0 cm bestaat dus uit drie significante cijfers.

Belangrijk is om te weten dat nullen aan de linkerkant van een meetwaarde niet meetellen als significante cijfers. De meetwaarde 0,0040 meter heeft dus slechts twee significante cijfers.

Maar wat nu als we een rekensommetje doen met verschillende meetwaarden? Op hoeveel cijfers moeten we het antwoord van dit sommetje dan afronden? De regel is dat we bij vermenigvuldigen en delen het antwoord schrijven in evenveel significante cijfers als de meetwaarde met het minst aantal significante cijfers. Laten we een voorbeeld bespreken. Stel een auto rijdt 200,0 meter in 20,6 seconden. Als we de snelheid op onze rekenmachine berekenen, dan vinden we:

$$ v = \frac{\Delta x}{\Delta t} $$ $$ v = \frac{200,0}{20,6} = 9,708737864 \text{ m/s}$$

200,0 heeft vier significante cijfers en 20,6 heeft er drie. Drie is het minst, dus we willen het antwoord ook op drie cijfers afronden:

$$ v = \frac{200,0}{20,6} = 9,71 \text{ m/s}$$

Nog een voorbeeld. Stel een ruimteschip vliegt 3000 meter in 2,0 seconden. De snelheid wordt dan:

$$ v = \frac{\Delta x}{\Delta t} $$ $$ v = \frac{3000}{2,0} = 1500 \text{ m/s} $$

3000 heeft vier significante cijfers en 2,0 heeft er twee. Het antwoord willen we dus ook maar in twee cijfers noteren. Maar hoe noteren we het getal 1500 in slechts twee cijfers? Dit doen we met behulp van machten van tien. We schrijven:

$$ v = \frac{3000}{2,0} = 1,5 \times 10^3 \text{ m/s} $$

Machten van tien werken als volgt. 1,5 × 10³ is gelijk aan 1500. Als we een waarde vermenigvuldigen met 10³, dan schuift de komma dus drie plaatsen op naar rechts. Het getal 15 × 10^-2 is gelijk aan 0,15. Als we een waarde vermenigvuldigen met 10^-2, dan schuift de komma dus twee plaatsen op naar links.

In de praktijk is het niet nodig om bij elke rekenstap het antwoord in het juiste aantal significante cijfers te schrijven. Bij het eindantwoord is dit echter wel verplicht! Als je het eindantwoord gevonden hebt, kijk dan terug in de vraag naar alle meetwaarden die je gebruikt hebt en ook naar de waarden uit BINAS die je gebruikt hebt en kijk welke waarde het minst aantal significante cijfers heeft. Schrijf je antwoord dan ook in dit aantal significante cijfers op.

Naast machten van tien is het soms ook mogelijk om voorvoegsels te gebruiken. Ook deze kan je in BINAS terugvinden. In de onderstaande tabel staan de bekendste voorvoegsels:

G	giga	109
M	mega	106
k	kilo	103
h	hecto	102
da	deca	101
d	deci	10-1
c	centi	10-2
m	milli	10-3
μ	micro	10-6
n	nano	10-9

Met voorvoegsels kunnen we een meetwaarde als 3,45 × 10^-6 m bijvoorbeeld ook schrijven als 3,45 μm.

Er zijn ook getallen in de natuurkunde die wel precies zijn. Neem bijvoorbeeld het aantal leerlingen in een klaslokaal, het aantal ramen in een gebouw, het aantal zijden van een vierkant enzovoorts. We noemen deze precieze getallen telwaarden. Omdat deze waarden precies zijn, hebben ze dus een oneindige hoeveelheid significante cijfers. Als gevolg is het bij berekeningen nooit nodig om naar de significante cijfers van telwaarden te kijken.

Leerdoelen:

Zorg dat je het aantal significante cijfers van een meetwaarde kan achterhalen. Denk eraan dat nullen aan de linkerkant niet meetellen. Zorg dat je telwaarden kan onderscheiden van andere meetwaarden. Bij telwaarden let je niet op significantie. Zorg dat je meetwaarden in een aantal significante cijfers kan omschrijven met behulp van tienmachten. Zorg dat je weet dat bij vermenigvuldigen en delen het antwoord wordt geschreven in evenveel significante cijfers als de meetwaarde met het minste aantal significante cijfers. Zorg dat je de voorvoegsels in de tabel uit de paragraaf kan gebruiken.

Opdrachten

(6p) Noteer het aantal significante cijfers van de volgende meetwaarden: 25,0 kg/m3 35600 m 12 km/h 0,350 m/s 0,000001 m 1,000001 m (2p) Beschrijf waar je op moet letten bij het bepalen van het aantal significante cijfers van een meetwaarde. (6p) Geef het aantal significante cijfers of geef aan dat er sprake is van een telwaarde: Een baksteen heeft een massa van 1 kg. De woonkamer heeft 3 grote ramen. De diameter van een cirkel is gelijk aan 2r. Er stromen per seconde 900 000 elektronen door de draad. Er stromen per seconde 900 × 103 elektronen door de draad. De spanning van het stopcontact is gelijk aan 230 V. (8p) Na een berekening geeft je rekenmachine de volgende waarden aan. Schrijf ze in de aangegeven hoeveelheid significante cijfers: Schrijf 2500 in twee significante cijfers. Schrijf 0,0150 in twee significante cijfers. Schrijf 150 in één significant cijfer. Schrijf 3400,8 in drie significante cijfers. Schrijf 1 500 000 in vier significante cijfers. Schrijf 0,00500000 in één significant cijfer. Schrijf 150 × 103 in twee significante cijfers. Schrijf 1800 × 10-5 in twee significante cijfers. (2p) Beschrijf hoe je het aantal significante cijfers bepaalt bij een berekening. Bereken de volgende opdrachten in het juiste aantal significante cijfers: (2p) Een sprinter rent 400,0 m en doet hier 55 seconden over. Bereken de snelheid van de sprinter. (2p) Een kamer heeft een lengte van 25,50 m en een breedte van 14 m. Bereken de oppervlakte van de kamer. (3p) Een cirkel heeft een diameter van 15,2 cm. Bereken de omtrek van de cirkel. (2p) Een kamer heeft een lengte van 5 m en een breedte van 3,51 m. Bereken de oppervlakte van de kamer. (5p) Een leerling denkt dat de massa van al de lucht in de kamer waarin hij staat zwaarder is dan hijzelf. De kamer heeft een lengte van 10 m, een breedte van 8 m en een hoogte van 2,5 m. Laat met een berekening zien of de leerling gelijk heeft of niet. (4p) Een stalen cilinder heeft een lengte van 10,0 m en een diameter van 2,00 cm. Bereken de massa van de stalen cilinder. (5p) 18-karaats goud bestaat voor 75% uit goud en voor de rest uit zilver. Een persoon heeft drie ringen gevonden van elk 10,4 gram bestaande uit 18-karaats goud. De persoon hoopt hiervan een mooi tweedehands brommertje te kopen ter waarde van 600 euro. Lukt dit? Metaal Euro/kilogram Koper 4,84 Zilver 466,34 Goud 30200,00

 

§2     Eenheden afleiden

In deze paragraaf gaan we leren de eenheid van onbekende grootheden te achterhalen. We noemen dit een eenheidsbeschouwing, of ook wel een eenheidsbepaling.

Om systematisch met eenheden te werken is een wiskundige notatie bedacht. Neem bijvoorbeeld de zin, "de eenheid van de massa is kilogram". Dit kunnen we wiskundig opschrijven als:

$$ [m] = kg $$

De vierkante haakjes betekenen dus "de eenheid van". We kunnen deze schrijfwijze gebruiken om eenheden van onbekende grootheden te achterhalen. We noemen dit ook wel een eenheidsbeschouwing of een eenheidsbepaling.

Stel bijvoorbeeld dat we de eenheid van de dichtheid willen weten, dan schrijven we:

$$ [\rho] = \frac{[m]}{[V]} = \frac{kg}{m^3}= \text{ kg/m}^3$$

De eenheid van de dichtheid is dus kg/m³.

Laten we nog een paar voorbeelden bespreken. Hieronder zien we de formule voor de versnelling (a):

$$ a = \frac{\Delta v}{\Delta t} $$

Stel we willen de eenheid van de versnelling weten, dan doen we:

$$ [a] = \frac{[\Delta v]}{[\Delta t]} = \frac{m/s}{s} = m/s^2 $$

De eenheid van de versnelling is dus m/s².

De formule voor de zwaartekracht (F_z) wordt gegeven door:

$$ F_z = mg $$

Omdat de eenheid van de valversnelling (g) gelijk is aan m/s², vinden we voor de zwaartekracht:

$$ [F_z] = [m][g] = kg \; m/s^2 $$

De eenheid van de kracht is in SI-grondeenheden dus gelijk aan kg m/s². Omdat deze eenheid een behoorlijke mond vol is, hebben we op een gegeven moment gekozen om deze eenheid simpelweg "newton" te noemen. We kunnen nu ook begrijpen waarom je eerder geleerd hebt dat je de massa in kilogram moet invullen in deze formule. Dit komt omdat de kilogram dus in de eenheid newton verstopt zit.

We hadden de formule ook kunnen gebruiken om juist de eenheid van de valversnelling te vinden. Dit doen we als volgt:

$$ [g] = \frac{[F_z]}{[m]} = \frac{N}{kg} = \frac{kg m/s^2}{kg} = m/s^2 $$

Leerdoelen:

Zorg dat je eenheden kan achterhalen met een eenheidsbepaling. Noteer hiervoor eerst de formule met rechte haken om elke grootheid. Deze rechte haken staan voor "de eenheid van". Zorg dat je weet dat [F] = N = kgm/s2 en dat je dit in BINAS kan opzoeken.

Opdrachten

(1p) De snelheid kunnen we berekenen met de formule v = Δx/Δt. Laat met deze formule zien dat de SI-eenheid van de snelheid meter per seconde is. Gebruik hiervoor de notatie uit de paragraaf. (1p) De eenheid van kracht is de newton. Geef de eenheid van kracht in SI-grondeenheden. Gebruik hiervoor de formule F = ma. (2p) De zwaartekracht kan worden berekend met de formule Fz = mg. Laat zien dat de eenheid van de constante g geschreven kan worden als N/kg en als m/s2. (2p) De kracht werkend op draaiende voorwerpen wordt gegeven door: $$ F = \frac{mv^2}{r} $$ F staat voor de kracht, m voor de massa, v voor de snelheid en r voor de baanstraal van de cirkelbeweging. Laat zien dat je met deze formule wederom vindt dat N = kgm/s2. (3p) Als je de afstand van een versnellend voorwerp wilt berekenen, dan doe je dat met deze formule: $$ \Delta x = v_b\Delta t + \frac{1}{2}a\Delta t^2 $$ Laat zien dat je aan beide kanten van de formule dezelfde eenheid vindt. De elektrische weerstand van een ijzeren draad is te berekenen met de volgende formule: $$ R = \frac{\rho l}{A} $$ l staat hier voor de lengte van de draad en A staat voor de oppervlakte van de doorsnede van de draad. De letter ρ is hier niet de dichtheid maar de zogenaamde soortelijke weerstand. Voor ijzer heeft de soortelijke weerstand een waarde van 105 × 10-9 Ωm. R is de weerstand gemeten in Ω. (2p) Laat met de formule zien dat de soortelijke weerstand inderdaad wordt gegeven in "Ohm keer meter". (2p) De draad heeft een lengte van 20,0 m en een doorsnede van 7,07 mm2. Bereken de weerstand van de draad. (2p) De energie (E) van een voorwerp is te berekenen met de volgende formule: $$ E = Fs $$ F is hier de kracht en s is de afstand die het voorwerp aflegt. Laat zien dat de eenheid voor de energie zowel gegeven kan worden in N × m als in kg m2/s2. (2p) De energie van een blokje aan een uitgerekte veer wordt gegeven door: $$ E_{veer} = \frac{1}{2}Cu^2 $$ u is hier de uitwijking en C is de veerconstante. Laat zien dat je hier dezelfde eenheid vindt voor de energie als bij de vorige vraag. Bepaal hiervoor eerst de eenheid van de veerconstante met behulp van de formule voor de veerkracht: $$ F_{veer} = Cu $$

 

§3     De raaklijn

In deze paragraaf gaan we leren hoe we in (x,t)-diagrammen de snelheid op een bepaald tijdstip kunnen bepalen. We doen dit met de zogenaamde raaklijn.

In het onderstaande (x,t)-diagram is de snelheid niet constant. Als we de snelheid op bijvoorbeeld tijdstip A willen bepalen, dan kunnen we dit doen door een klein driehoekje te tekenen en hiermee de snelheid te berekenen (zie de linker afbeelding). Dit is echter lastig meten en levert daardoor een zeer onnauwkeurig antwoord op. We kunnen dit probleem oplossen door het kleine lijnstukje in beide richtingen zoveel mogelijk te verlengen (zie de rechter afbeelding). De verlengde lijn noemen we een raaklijn. Omdat de raaklijn net zo steil loopt als het oorspronkelijke lijntje vinden we hier dezelfde snelheid.

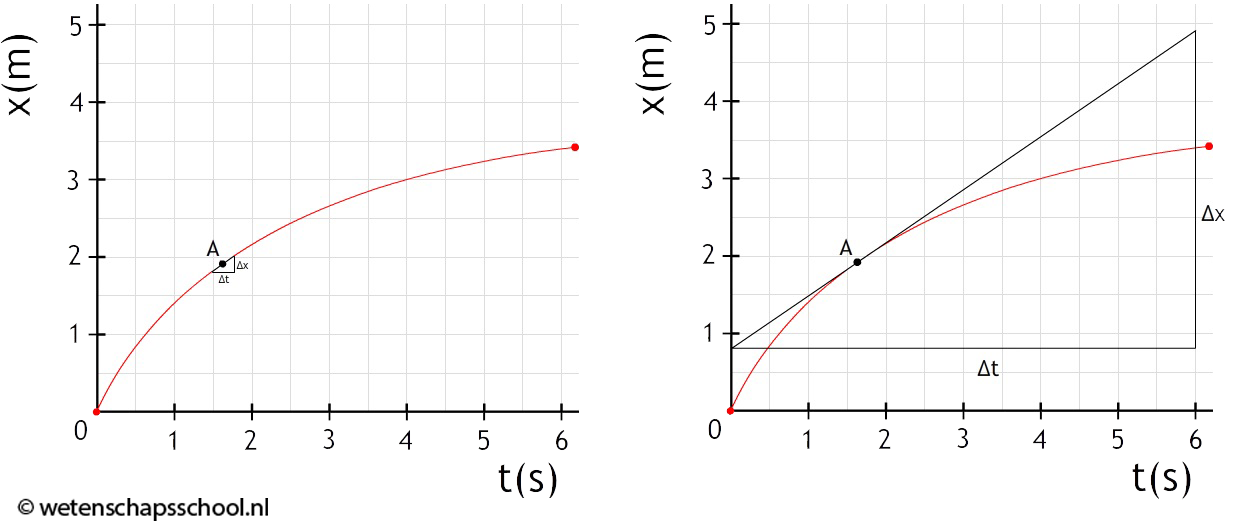
De snelheid op tijdstip A is in dit geval gelijk aan:

$$ v = \frac{4,0}{6,0} = 0,67 \text{ m/s} $$

Er geldt dat hoe steiler de raaklijn loopt, hoe groter de snelheid is.

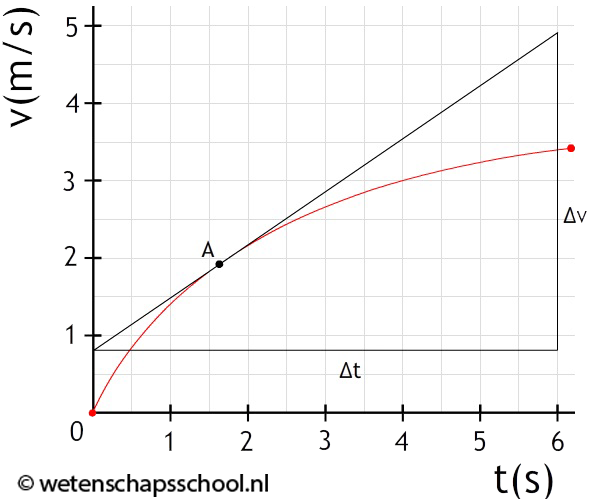
We kunnen iets soortgelijks doen in een (v,t)-diagram. In dit type diagram is de raaklijn gelijk aan de versnelling op een specifiek tijdstip. Er geldt dat hoe steiler de raaklijn loopt, hoe groter de versnelling is.

Leerdoelen:

Zorg dat je de snelheid op een tijdstip kan bepalen in een (x,t)-diagram met behulp van een raaklijn. Zorg dat je de versnelling op een tijdstip kan bepalen in een (v,t)-diagram met behulp van een raaklijn.

Opdrachten

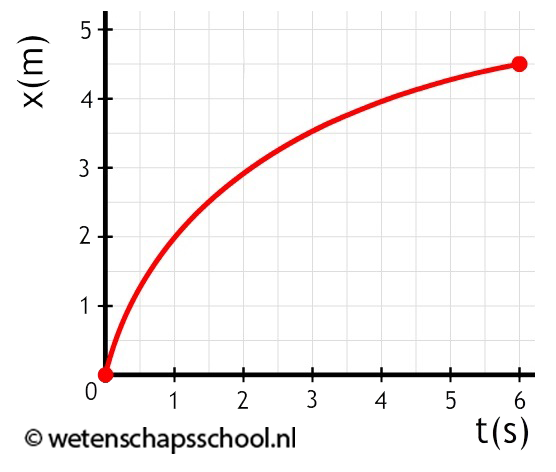
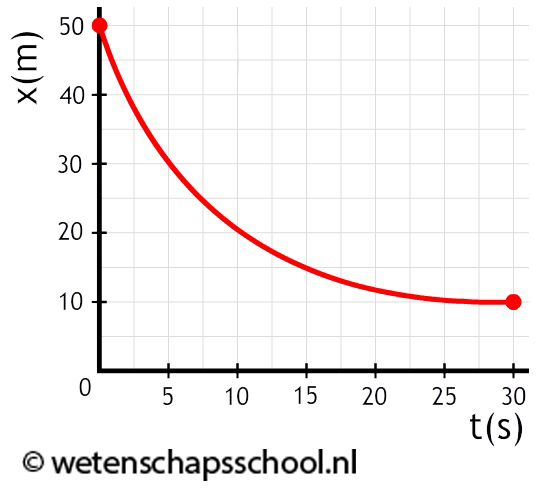
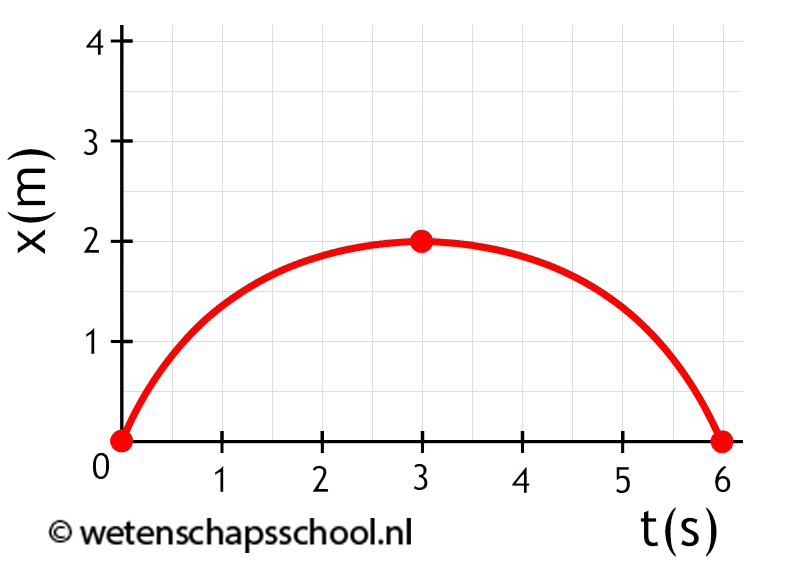
(3p) Bepaal de snelheid op tijdstip t = 2,0 s: (3p) Bepaal de snelheid op tijdstip t = 5,0 s. (7p) Bepaal de beginsnelheid, de eindsnelheid en de snelheid op tijdstip t = 3,0 s. (3p) Een persoon geeft een duw tegen een bal. Hieronder wordt de beweging van deze bal beschreven. Op tijdstip t = 0 s kwam de bal los van de hand van de persoon. Bepaal de beginsnelheid van de bal. 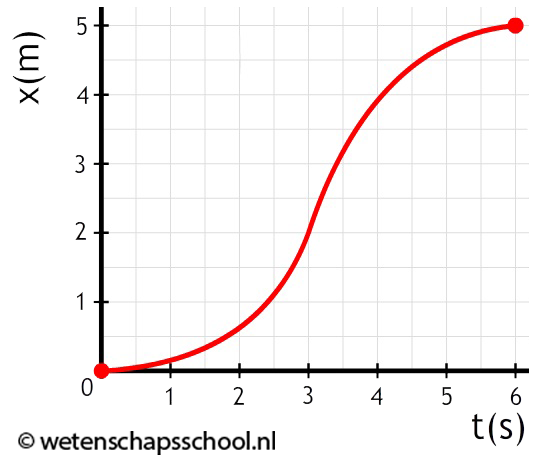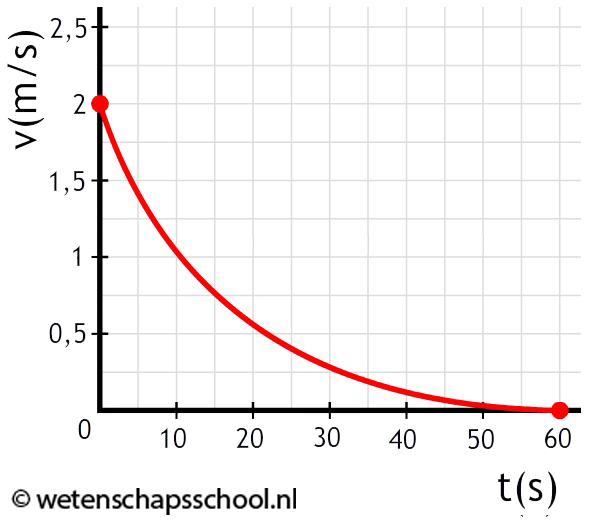(3p) Bepaal de maximale snelheid in het volgende diagram: (3p) Bepaal de versnelling op tijdstip t = 20 s: (4p) Hieronder is de beweging van een optrekkende auto beschreven. Bepaal de maximale versnelling en de maximale snelheid tijdens de beweging. 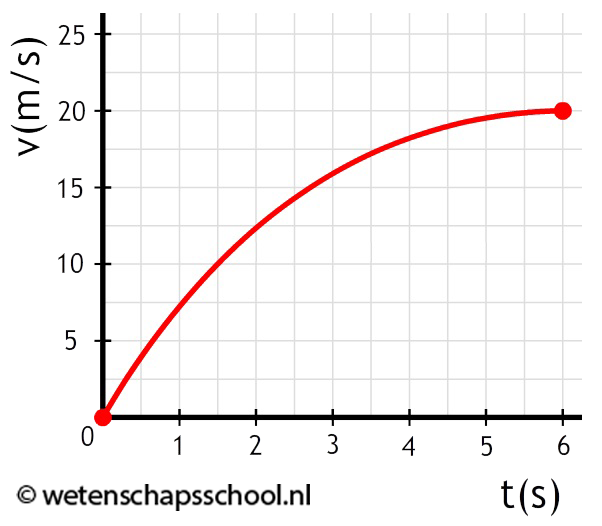(5p) Bepaal de versnelling op tijdstip t = 1,0 s en t = 4,0 s. 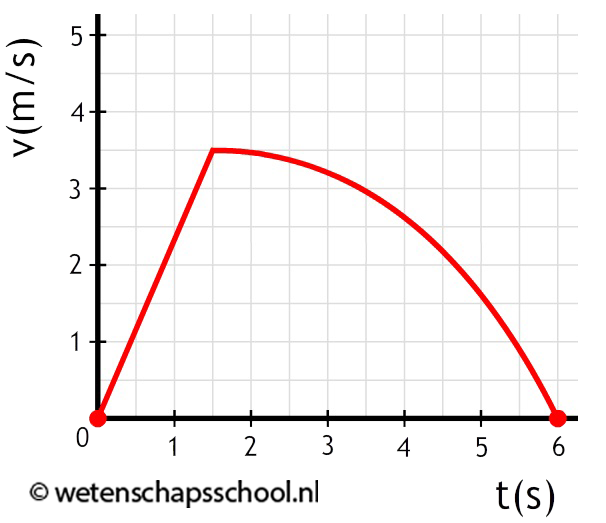In het onderstaande (v,t)-diagram zien we de versnelling van een karretje op een horizontale baan aan het begin van een supersnelle achtbaan. 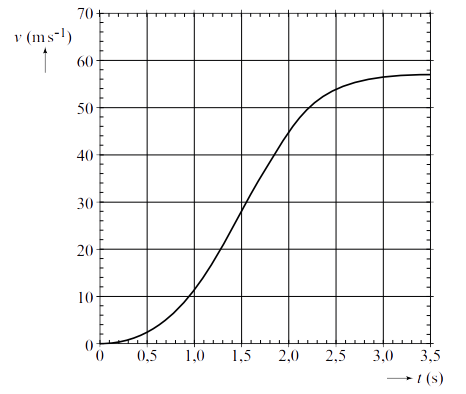(1p) Een leerling analyseert de grafiek en concludeert dat we hier eerst te maken hebben met een versnelling en dat het voorwerp daarna vertraagt totdat de snelheid constant is. Heeft de leerling gelijk? (3p) Vind de maximale versnelling die de achtbaankar ondergaat. (bron: examen VWO 2010-1)

 

§4     De tweede wet van Newton

In deze paragraaf gaan we rekenen met de tweede wet van Newton. Deze wet vertelt ons hoe groot de resulterende kracht is werkend op een versnellend voorwerp.

In het hoofdstuk "Kracht" hebben we geleerd dat de eerste wet van Newton ons vertelt dat de resulterende kracht nul is als de snelheid van een voorwerp constant is. De tweede wet van Newton vertelt ons wat er gebeurt als de resulterende kracht niet nul is. In dat geval geldt:

$$ F_{res} = ma $$ Versnelling (a) meter per seconde per seconden (m/s2) Resulterende kracht (Fres) newton (N) Massa (m) kilogram (kg)

De formule wordt ook vaak in de volgende vorm geschreven:

$$ a = \frac{F_{res}}{m} $$

In deze vorm is goed te zien dat een voorwerp versnelt als er een resulterende kracht op werkt. Ook zien we dat deze versnelling kleiner wordt als de massa van het voorwerp groter is. Voorwerpen met een grote massa zijn dus moeilijk in beweging te krijgen en ook moeilijk af te remmen. Hoe groter de massa van een voorwerp is, hoe moeilijker het dus is om de snelheid van dit voorwerp te veranderen. We noemen dit principe traagheid.

EXPERIMENT

In het rechter filmpje dat is gemaakt in het International Space Station (ISS), is dit fenomeen goed te zien: DEMO-VIDEO: De tweede wet van Newton

EXPERIMENT

In het rechter filmpje kunnen we het effect van traagheid zien op een aantal blokken die op een trampoline liggen. Als een persoon op de trampoline springt, duurt het even voordat het vallen van de blokken echt op gang komt. DEMO-VIDEO: Traagheid

We merken traagheid ook als je in een auto zit die krachtig remt. De auto komt snel tot stilstand, maar de inzittenden schieten dan nog een stukje door naar voren (tot ze worden tegengehouden door hun gordels). Dit komt door de traagheid van de inzittenden. Ze willen doorbewegen met de snelheid die ze al hadden.

Als een stilstaande auto van achter wordt geraakt, dan schiet de auto naar voren, maar de inzittenden willen door traagheid op hun plek stil blijven staan. Als gevolg heb je het gevoel dat je in je stoel wordt gedrukt (maar eigenlijk sta jij stil en drukt de stoel juist tegen jou aan).

Voorbeeld

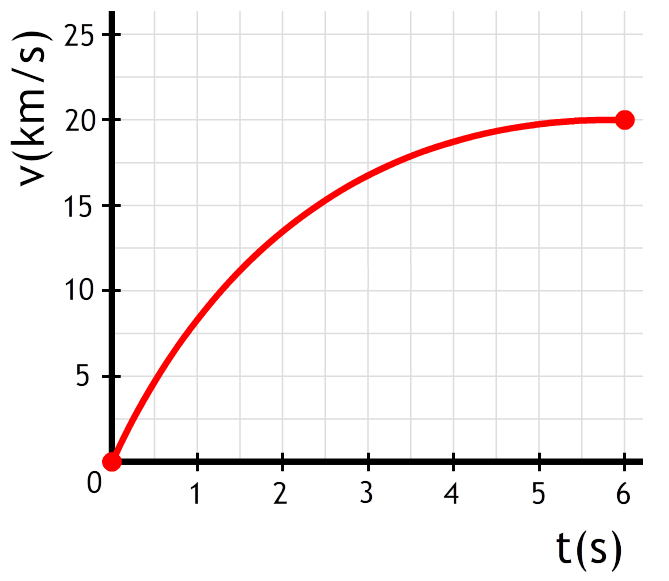
Vraag: In het onderstaande (v,t)-diagram is het opstijgen van een raket beschreven. De raket heeft een massa van 2,8 × 106 kg. Bepaal de motorkracht van de raket op het moment dat deze wordt afgeschoten. Antwoord: Met behulp van een raaklijn op t = 0 s vinden we de versnelling (zie de onderstaande afbeelding). Met behulp van de raaklijn vinden we de volgende versnelling: $$ a = \frac{\Delta v}{\Delta t} = \frac{25000}{2,5} = 1,0 \times 10^4 \text{ m/s}^2 $$ Let er op dat de snelheid in het diagram in kilometer per seconde staat. 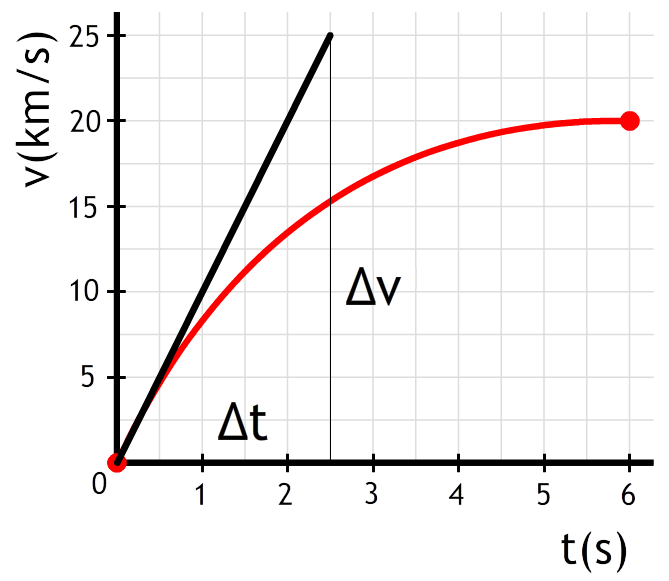Met de tweede wet van Newton kunnen we nu de resulterende kracht berekenen: $$ F_{res} = ma = 2,8 \times 10^6 \times 1,0 \times 10^4 = 2,8 \times 10^{10} \text{ N} $$ Dit is echter nog niet het antwoord. We willen niet de resulterende kracht weten, maar de motorkracht. In deze situatie werkt op de raket een motorkracht omhoog en een zwaartekracht omlaag. Er geldt dus: $$ F_{res} = F_m - F_z $$ Dit kunnen we omschrijven tot: $$ F_m = F_{res} + F_z $$ Als we dit invullen, dan vinden we: $$ F_{m} = 2,8 \times 10^{10} + 2,8 \times 10^6 \times 9,81 = 2,8 \times 10^{10} \text{ N} $$

Leerdoelen:

Zorg dat je kan rekenen met de tweede wet van Newton (Fres = ma). Zorg dat je weet dat de resulterende kracht vaak uit meerdere krachten bestaat. Bij een rijdende auto geldt bijvoorbeeld "Fres = Fm - Fw". Zorg dat je weet dat de formule "a = Fres/m" ons vertelt dat voorwerpen met een grote massa moeilijk te versnellen en moeilijk te vertragen zijn. Hoe zwaarder het voorwerp, hoe lastiger de snelheid ervan te veranderen is. We noemen dit traagheid. Zorg dat je voorbeelden kan noemen waarbij traagheid een rol speelt. Denk bijvoorbeeld aan het doorschieten van passagiers bij het remmen van een auto.

Opdrachten

(1p) Een groot vrachtschip komt lastig tot stilstand. Leg dit uit met het begrip traagheid. (1p) Een docent trekt snel een kleed onder een servies vandaan. Wonderbaarlijk genoeg blijft het servies staan. Leg uit hoe dit kan met het begrip traagheid. Een metro komt krachtig remmend tot stilstand. De passagiers van de metro die staan worden hierdoor een meter verplaatst ten opzichte van de metro. (1p) In welke richting verplaatsen de passagiers. In de bewegingsrichting van de metro of tegen de bewegingsrichting in. (1p) Leg uit waarom dit gebeurt. (1p) Aan het einde van de rit remt het treintje van een achtbaan af. Hierdoor worden de inzittenden tegen de veiligheidsbeugels geduwd. Verklaar dit met het begrip traagheid. (1p) Leid de eenheid van de kracht af in SI-grondeenheden met behulp van de volgende formule: $$ F_{res} = ma $$ Een persoon duwt een blok met een massa van 30 kilogram. Als gevolg versnelt het blok met 0,60 m/s2. (2p) Bereken de resulterende kracht die op het blok werkt. (2p) De wrijvingskracht die op het blok werkt was tijdens de versnelling gelijk aan 15 N. Bereken hiermee de spierkracht van de persoon. Een auto versnelt vanuit stilstand naar 100 km/h in 25 seconden. De auto heeft een massa van 3,5 × 103 kg. (5p) Bereken de resulterende kracht die op de auto werkt. (2p) De wrijvingskracht die op de auto werkt tijdens het optrekken was gelijk aan 3,0 × 103 N. Bereken hiermee de motorkracht van de auto. 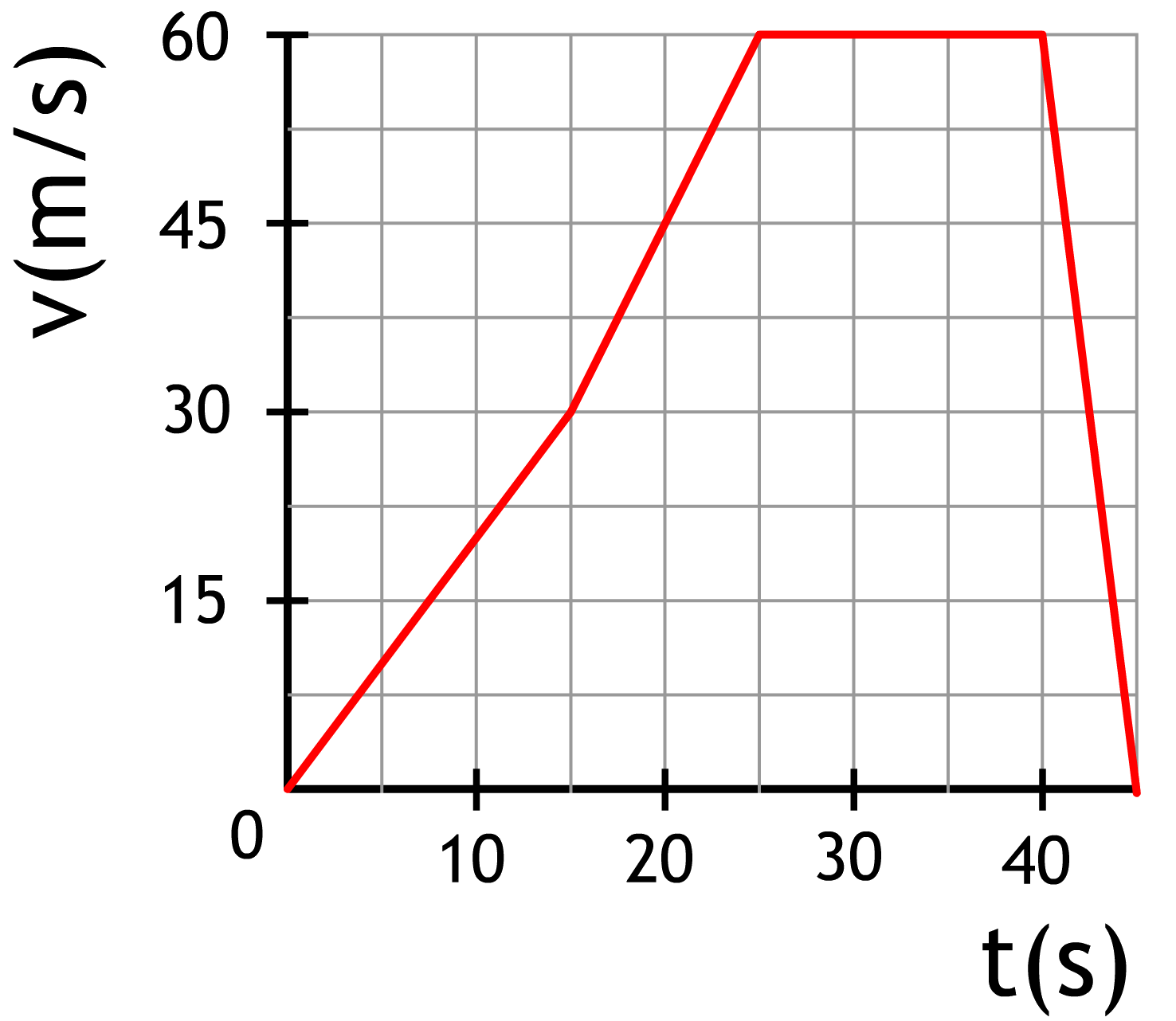(8p) Hieronder is een (snelheid,tijd)-diagram weergegeven van een bewegend voorwerp met een massa van 3,0 × 103 kg. Bepaal met behulp van de grafiek op elk moment de resulterende kracht. Het onderstaande (v,t)-diagram beschrijft een sprong van een volleybalspeler met een massa van 75 kg. 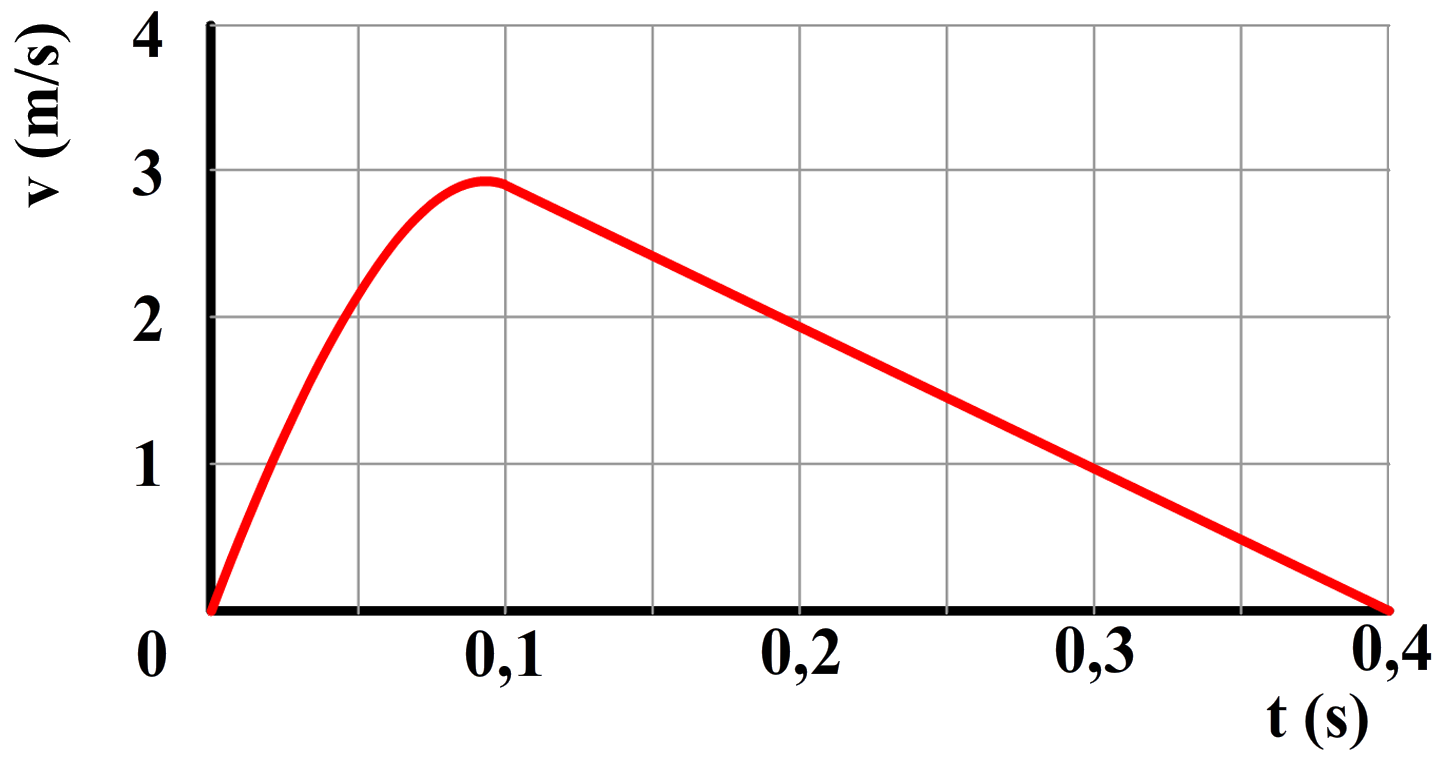(4p) Bepaal de resulterende kracht werkende op de springer op tijdstip t = 0 s. (2p) Bepaal de afzetkracht van de springer op tijdstip t = 0 s. 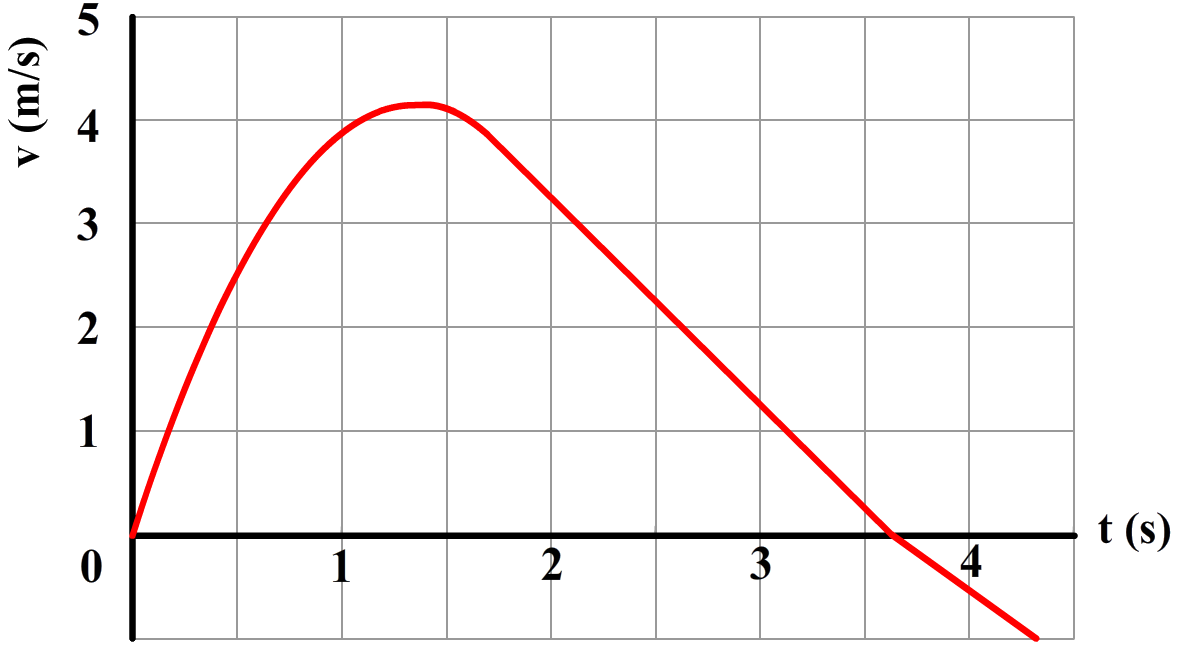(bron: examen VWO 2015-1) (5p) Space Shot is een spectaculaire attractie in het pretpark Six Flags. Hierbij kan een groep mensen zich laten lanceren met behulp van een ring om een hoge toren. De massa van de ring met bezoekers is 2,4 × 103 kg. Hieronder zien we een (v,t)-diagram van de beweging. Bepaal de motorkracht waarmee de ring wordt afgeschoten. Je mag de wrijvingskracht verwaarlozen. (Afbeelding: Loozrboy; CC BY-SA 2.0) (bron: examen VWO 2003-1) (6p) Een auto met een massa van 3,0 × 103 kg versnelt eenparig van 50 km/h naar 70 km/h in een tijdsduur van 12 seconden. De motorkracht van de auto tijdens de beweging heeft een constante waarde van 1,5 × 103 N. Bereken de grootte van de wrijvingskracht tijdens deze versnelling. (4p) Tegen het einde van de Eerste Wereldoorlog introduceerde het Duitse leger het Parijse Kanon. Dit kanon kon Parijs beschieten van achter de frontlinie, op een afstand van 120 km. De loop was extra lang gemaakt, zodat de granaten een voldoende hoge snelheid kregen om de afstand te overbruggen. Hieronder zien we het (v,t)-diagram en het (Fres,t)-diagram van een granaat weergegeven tijdens het afschieten. Op t = 0,04 s verlaat de granaat de loop. Bepaal met behulp van de diagrammen de massa van de granaat. 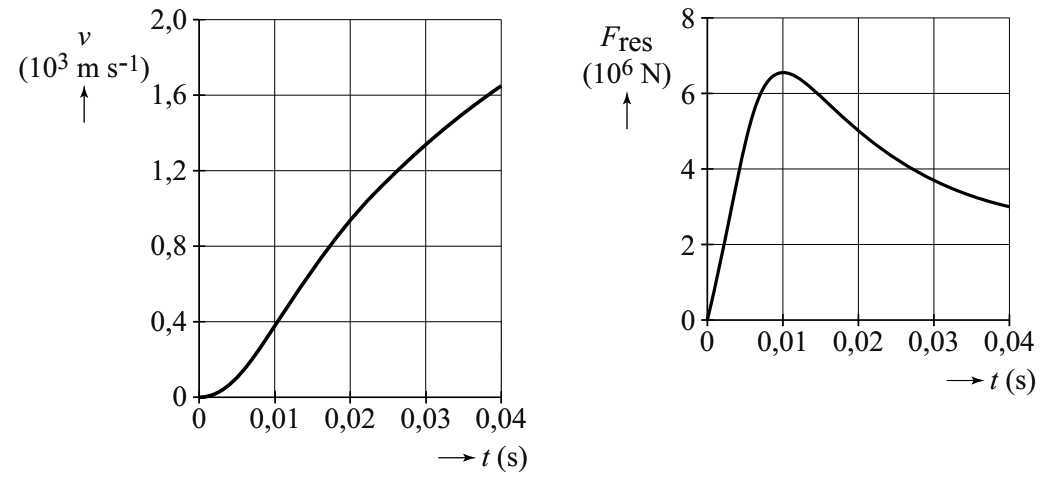(bron: examen VWO 2019-2)

BINAS:
2	Voorvoegsels
3-5	Grootheden en eenheden
35	Formules