Extra stof hoofdstuk kwantummechanica
Het Bohratoom
Aan het eind van de 19de eeuw dachten wetenschappers dat de natuurkunde zo goed als af was. Newton had de succesvolle theorie voor de zwaartekracht gevonden en Maxwell kon met zijn elektrodynamica zowel elektrische en magnetische velden beschrijven. Maxwell ontdekte ook dat licht niets anders is dan een elektromagnetische golf die ontstaat bij het versnellen van geladen deeltjes.
Er waren in de tijd echter nog een paar problemen die destijds nog klein leken. Deze problemen maakten echter uiteindelijk een einde maken aan de klassieke natuurkunde. Het eerste probleem was dat de snelheid van het licht in de elektrodynamica niet afhankelijk leek van de snelheid van de waarnemer van dit licht. Dit probleem werd uiteindelijk opgelost met Einstein's speciale relativiteitstheorie.
Een tweede probleem ging over straling. Als je een voorwerp opwarmt, dan zendt het straling uit beschreven door de Planck-kromme. De vorm van deze kromme kon niet worden begrepen met de theorie van Maxwell. Max Planck vond een formule die deze kromme beschreef. Hij kon deze formule echter niet verklaren:
$$ I = \frac{8\pi hf^3}{c^3}\frac{1}{e^{hf/kT}-1} $$Vooral de term 'hf' in deze formule liep veel vragen op. Einstein toonde door middel van zijn studie naar het fotoelektrisch effect aan dat licht bestond uit deeltjes, fotonen genaamd, en dat deze term 'hf' gelijk was aan de energie van één zo'n foton. Maar hoe kan licht enerzijds uit elektromagnetische golven bestaan en anderzijds uit fotonen? Golven zijn immers uitgebreid in de ruimte en kunnen interferen, terwijl deeltjes juist een precieze locatie hebben en niet kunnen interferen. Dat licht zowel deeltje- als golfeigenschappen heeft leek logisch onmogelijk, maar toch was dit de enige manier om de theorie te beschrijven. We noemen dit in de kwantummechanica de golf-deeltjedualiteit.
Een ander probleem met straling was dat alleen licht van bepaalde specifieke golflengte kan absorberen en uitstralen. Licht van andere golflengtes scheen gewoon dwars door de atomen heen. Hieronder zien we bijvoorbeeld de kleuren licht die waterstof kan absorberen en uitzenden. Ook dit werd niet begrepen. Waarom alleen deze golflengtes?

In een poging het mysterie op te lossen, stelde Balmer een formule op die de correcte positie van de waterstoflijnen beschreef,de zogenaamde Balmer formule gevonden:
$$ \lambda = \frac{91,18 \text{ nm}}{\frac{1}{m^2}-\frac{1}{n^2}} $$Hier is m een heel getal groter dan nul en n een heel getal groter dan m. Balmer kan hiermee de lijnen van waterstof goed beschrijven, maar hij kon niet verklaren waar deze relatie vandaan kwam.
Nog een laatste probleem met straling. Rutherford had ontdekt dat een atoom voornamelijk uit lege ruimte bestaat, met in het midden een relatief zware kern en daaromheen lichte elektronen. In een eerste poging werd het atoom vergeleken met het zonnestelsel. Wellicht dat de elektronen aangetrokken worden tot het proton en door de middelpuntzoekende kracht in een stabiele baan om de atoomkern bewegen. Het probleem is echter dat de middelpuntzoekende versnelling die zo'n deeltje ondergaat er voor zou moeten zorgen dat het deeltje straling uitzendt. Hierdoor zou het elektron in zijn baan voortdurend energie kwijtraken en als gevolg de atoomkern in vallen. Een atoom zou volgens de klassieke natuurkunde dus niet eens kunnen bestaan!
Al deze problemen werden uiteindelijk opgelost door een theorie die de oude natuurkunde zou vervangen: de kwantummechanica.
Het Bohr atoom
De verklaring voor het merkwaardige spectrum van waterstof werd ontdekt door Niels Bohr. Hij begon zijn redenering met het klassieke idee dat het elektron in waterstof in zijn baan wordt gehouden door een middelpuntzoekende kracht. Deze middelpuntzoekende kracht werd geleverd door de elektrische aantrekkingskracht van het proton. Er geldt dus:
$$ F_{elek} = F_{mpz} $$ $$ \frac{fe^2}{r^2} = \frac{mv^2}{r} $$ $$ \frac{fe^2}{r} = mv^2 $$Toen maakte Bohr een bijzondere stap. Hij vergelijk het elektron in het waterstof atoom met een trillende snaar. Het geluidsspectrum van een muziekinstrument toonde pieken bij specifieke frequenties die overeenkwamen met staande golven - de grondtoon en de boventonen. Dit leek enorm of de specifieke frequenties van licht in het lichtspectrum van waterstof. Wellicht vormde het elektron in waterstof ook wel een staande golf.
In de onderstaande afbeelding zien we de mogelijke staande golven die het elektron in zijn baan om de atoomkern kan aannemen. Het elektron kan zich nu alleen in bepaalde schillen bevinden die overeenkomen met de staande golven die het elektron kan vormen. Om ervoor te zorgen dat het begin en einde van de golf goed op elkaar aansluiten, moet er in elke baan een volledig aantal golven passen. Er geldt dus:
$$ 2\pi r = n\lambda $$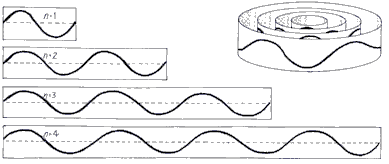
In het hoofdstuk over relativiteit hebben we gezien dat voor licht geldt dat E = pc. Als we dit combineren met E = hf, dan vinden we:
$$ hf = pc $$ $$ h\frac{c}{\lambda} = pc $$Dit kunnen we omschrijven tot:
$$ p = \frac{h}{\lambda} $$Louis de Broglie dacht dat deze formule voor licht wellicht ook geldt voor deeltjes met massa, zoals een elektron. In dat geval zou de impuls p natuurlijk niet gelijk zijn aan 'E/c', maar aan 'mv'. We zullen in de rest van deze paragraaf aantonen dat we met deze aanname het waterstofspectrum kunnen begrijpen.
Als we \( 2\pi r = n\lambda \) combineren met de De Broglie formule, dan vinden we:
$$ v_n = \frac{n\hbar}{ mr} $$Deze formule geeft ons de snelheid van het elektron in deze verschillende schillen.
Als we dit substitueren in de formule voor de elektrische kracht (\( fe^2 / r = mv^2 \)), dan vinden we:
$$ \frac{fe^2}{r^2} = \frac{n^2\hbar^2}{ mr^3} $$Dit kunnen we herschrijven tot:
$$ r_n = n^2\frac{ \hbar^2}{ fme^2} $$ $$ n = 1,2,3,... $$Hier hebben we de afstand tussen het proton en het elektron gevonden bij de verschillende schillen. We korten deze formule vaak als tot:
$$ r_n = n^2r_B $$ $$ r_B = \frac{\hbar^2}{ fme^2} $$rB wordt de Bohrstraal genoemd. De Bohrstraal is in BINAS tabel 7 te vinden en heeft de waarde 5,29 × 10-11 m.
Nu gaan we naar de energie van het elektron kijken. Voor het elektron in zijn baan om het proton geldt:
$$ E_{tot} = E_{kin} + E_{elek} $$ $$ E_{tot} = \frac{1}{2}mv^2 - \frac{fe^2}{ r} $$Met behulp van de \( fe^2 / r = mv^2 \) en \( r_n = n^2r_B \) vinden we hiermee dat:
$$ E_n = \frac{1}{2}\left( \frac{fe^2}{ n^2 r_B} \right) - \frac{fe^2}{n^2r_B} $$Dit kunnen we versimpelen tot:
$$ E_n = -\frac{1}{n^2}\left(\frac{fe^2}{2 r_B}\right) $$Als we de constantes samenvoegen, dan vinden we:
$$ E_n = -\frac{13,60 \text{ eV}}{n^2} $$Voor n = 1 vinden we een energie van -13,60 eV. Dit is precies de experimentele waarde voor de ionisatie-energie van waterstof!
Bohr bedacht toen het volgende. Een elektron in waterstof in een bepaalde schil, kan alleen een foton absorberen als dit foton genoeg energie heeft om het elektron naar een hogere schil te tillen. Andersom geldt ook, het elektron kan alleen een foton uitstralen met een energie waarmee het elektron naar een lagere schil kan terugvallen. Stel bijvoorbeeld dat het elektron valt van schil n naar schil m. In dat geval heeft het foton dus een energie gelijk aan:
$$ \Delta E = E_f $$ $$ E_n - E_m = hf $$Als we de bovenstaande formule voor de energie hierin invullen, dan vinden we:
$$ E_n - E_m = -\frac{1}{n^2}\left(\frac{fe^2}{2 r_B}\right) - -\frac{1}{m^2}\left(\frac{fe^2}{2 r_B}\right) = \frac{fe^2}{2 r_B} \left(\frac{1}{m^2}-\frac{1}{n^2}\right) = hf$$Met \( f = c/\lambda \) wordt dit:
$$ \lambda_{n\rightarrow m} = \frac{2 hcr_B/(fe^2)}{\left(\frac{1}{m^2}-\frac{1}{n^2}\right)} $$Als we de constantes uitwerken, dan vinden we:
$$ \lambda_{n\rightarrow m} = \frac{91,18 \text{ nm}}{\left(\frac{1}{m^2}-\frac{1}{n^2}\right)} $$Dit is precies de formule van Balmer! Bohr kon met zijn theorie dus zowel de ionisatie-energie van waterstof als het waterstofspectrum verklaren!
Het Bohratoom was dus een groot succes, maar het bleek niet het hele verhaal. Het model werkte bijvoorbeeld niet voor complexere atomen. De volgende stap was de ontwikkeling van een kwantummechanica door Schrodinger.