Extra stof hoofdstuk kracht
Behoud van Impulsmoment
Met behulp van de wetten van Newton kunnen we een aantal grootheden vinden die constant blijven in de tijd. We noemen dit behouden grootheden. Het bekendste voorbeelden hiervan zijn behoud van energie en behoud van impuls. Deze behoudswetten gaan we in klas 5 bespreken. In deze paragraaf bestuderen we het behoud van impulsmoment (L)
Voor deze behoudswet definiëren we eerst het zogenaamde moment (M):
$$ \vec{M} = \vec{r} \times \vec{F} $$r is hier wederom de radiusvector en F is de kracht die op het voorwerp werkt. Het kruisje staat hier voor het kruisproduct. De definitie hiervan is:
$$ \vec{A} \times \vec{B} = AB\sin{\theta} $$De hoek θ is hier de hoek tussen de richting van A en B. Merk op dat als A en B in dezelfde of in tegengestelde richting wijzen, dat de sinus gelijk aan nul wordt en dat hierdoor het hele kruisprodukt nul wordt.
Naast het moment definiëren we ook het impulsmoment (L):
$$ \vec{L} = \vec{r} \times \vec{p} $$p hebben we eerder gezien. Dit is de impuls, gegeven door p = mv.
Als we de afgeleide van het impulsmoment naar de tijd nemen, dan vinden we met de produktregel dat:
$$ \dot{L} = \frac{d(\vec{r} \times \vec{p} )}{dt} = \vec{v} \times \vec{p} + \vec{r} \times \vec{F} $$Met M = r × F kunnen we dit herschrijven tot:
$$ \dot{L} = m \vec{v} \times \vec{v} + \vec{M} $$De linker term wordt nul, omdat beide vectoren v in dezelfde richting wijzen en als gevolg is de sinus in het kruisproduct nul. We vinden dus:
$$ \dot{L} = \vec{M} $$In situaties waarbij het moment M nul is, vinden we:
$$ \dot{L} = 0 \;\;\;\; \text{(als M = 0)} $$In dit geval is L dus constant en dus een behouden grootheid. Maar in welke gevallen in M nul? Het moment is het kruisprodukt tussen F en r. Als F en r in dezelfde of tegenovergestelde richting wijzen, dan is het moment dus nul (want sin(0)=0 en sin(180)=0). Dit gebeurt bijvoorbeeld bij voorwerpen die in een cirkelbaan bewegen. Neem bijvoorbeeld een planeet die om de zon beweegt. De radiusvector wijst van de zon naar de planeet en de kracht wijst van de planeet naar de zon. r en F wijzen hier dus in tegenovergestelde richting en M wordt hierdoor dus nul.
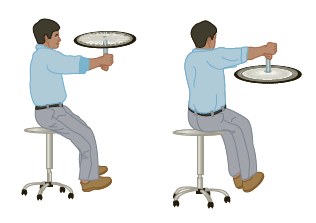
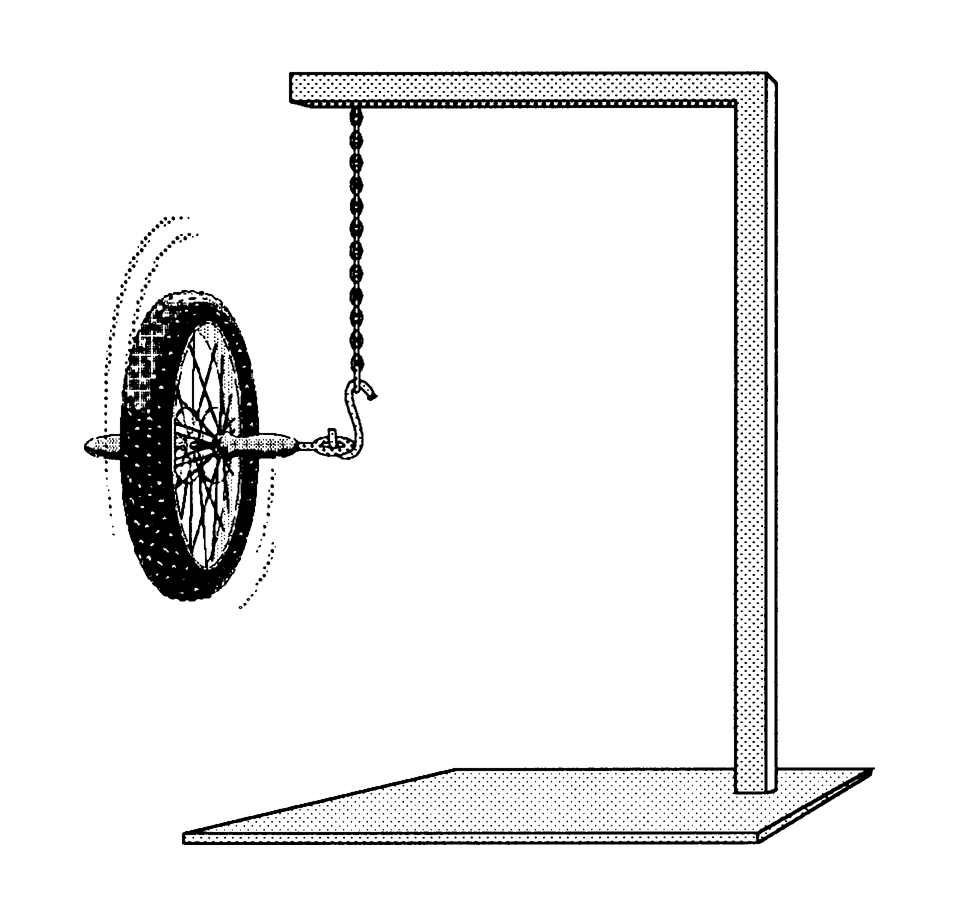
Wat kunnen we hiermee? Als L constant is, dan weten we dat r × mv constant is. Stel dat een planeet in een ellipsbaan om de zon beweegt, dan zal de r in de tijd veranderen. Als de r kleiner wordt, dan moet volgens het behoud van impulsmoment de snelheid groter worden. Dit is precies wat we zien. Ditzelfde effect heb je bijvoorbeeld ook als je een steen aan een touw rondslingert en dan de steen meer naar je toe trekt. De snelheid van de steen zal toenemen.
 Rekenen met impulsmoment
Rekenen met impulsmoment
|
|