Extra stof
Statistiek

Statistiek is één van de krachtigste wiskundige tools die je ooit zult leren. Je kan hiermee zowat elk onderwerp (zelfs onderwerpen uit de sociologie en psychologie) op een wetenschappelijke manier bestuderen. In deze tekst gaan we de basistechnieken behandelen waarmee jij meteen aan de slag kan.

De standaard deviatie

De twee belangrijkste begrippen uit de statistiek zijn het gemiddelde (μ) en de standaard deviatie (σ). Het eerste begrip kennen we natuurlijk allemaal. Neem bijvoorbeeld het gemiddelde van bijvoorbeeld de lengte van leerlingen in een klas. Dit kunnen we vinden door alle meetwaarden (x_i) bij elkaar op te tellen en te delen door het totaal aantal leerlingen (N):

$$ \mu = \frac{(x_1 + x_2 + ... + x_N)}{N} $$

Dit schrijven we als volgt beknopter op:

$$ \mu = \frac{1}{N} \sum_{i=0}^N{x_i} $$

Soms gebruiken we in plaats van de term "gemiddelde" ook wel de term verwachtingswaarde (E). We schrijven dan:

$$ \mu = E[x_i] $$

Stel dat we nu de gemiddelde lengte van alle Nederlanders van een bepaalde leeftijd willen bepalen, dan is het niet realistisch om iedereen te meten. In plaats daarvan nemen we een steekproef. In dat geval gebruiken we voor het gemiddelde het symbool x̄:

$$ \bar{x} = \frac{1}{N} \sum_{i=0}^N{x_i} $$

Dit gemiddelde zal hoogstwaarschijnlijk in de buurt liggen van μ (vooral bij grote N), maar het zal meestal toch iets afwijken.

Naast het gemiddelde is ook de spreiding van data van belang. We kunnen ons bijvoorbeeld afvragen in hoeverre de lengte van leerlingen in een klas uiteenloopt. Hoe verder de meetwaarden af zitten van het gemiddelde, hoe groter de spreiding. Een voor hand liggende manier de spreiding te meten is door het gemiddelde te bepalen van hoever elk meetpunt van het gemiddelde af zit. We doen dit door telkens de gemiddelde waarde van een meetwaarde af te halen, deze waarden tellen we allemaal bij elkaar op en delen we door N. We schrijven dit als volgt wiskundig op:

$$ \text{spreiding (1)} = \frac{1}{N} \sum_{i=0}^N (x_i - \mu) $$

Deze formule blijkt echter niet te werken. Als de meetwaarde boven het gemiddelde zit, dan wordt (x_i - μ) positief, maar als de meetwaarde onder het gemiddelde zit, dan wordt dit negatief. Als we alle negatieve en positieve waarden bij elkaar optellen, dan komen we op nul uit. Deze eerste poging werkt dus niet. Een voor de hand liggende poging om dit probleem op te lossen is door de absolute waarde van (x_i - μ) te nemen. Dan worden alle waarden positief krijgen we wel een gemiddelde boven de nul. Er geldt dan:

$$ \text{spreiding (2)} = \frac{1}{n} \sum_{i=0}^N \lvert x_i - \mu \lvert $$

Maar ook deze formule heeft een probleem. Als (x_i - μ) bijvoorbeeld de waarden 4, 4, -4 en -4 heeft, dan vinden we een gemiddelde van (4+4+4+4)/4 = 4. Als (x_i - μ) echter bijvoorbeeld 7, 1, -2 en -6 is, dan vinden we ook (7+1+2+6)/4 = 4. We vinden dus in beide gevallen hetzelfde antwoord, terwijl in het tweede geval de getallen tot echt meer verspreid zijn!

Dit brengt ons tot de correcte definitie. Wat we gaan doen is dat we (x_i - μ) gaan kwadrateren, daarna tellen we deze waarden bij elkaar op en delen we door het aantal metingen. Uiteindelijk trekken we weer de wortel. Het kwadraat heeft het voordeel dat het alle waarden positief maakt en dat het waarden die verder van het gemiddelde liggen zwaarder mee weegt. We noemen deze definitie van de spreiding de standaard deviatie (σ):

$$ \sigma = \sqrt{\frac{1}{N} \sum_{i=0}^N (x_i - \mu)^2} $$

Voor de twee bovenstaande getallenvoorbeelden vinden we in dit geval:

$$ \sigma = \sqrt{\frac{4^2+4^2+4^2+4^2}{4}} = 4 $$ $$ \sigma = \sqrt{\frac{7^2+1^2+2^2+6^2}{4}} = 4,74 $$

We vinden in het tweede voorbeeld nu inderdaad een grotere spreiding! Ook zien we dat in deze definitie een verdubbeling van de waarden een dubbel zo grote spreiding geeft:

$$ \sigma = \sqrt{\frac{8^2+8^2+8^2+8^2}{4}} = 8 $$ $$ \sigma = \sqrt{\frac{14^2+2^2+4^2+12^2}{4}} = 9,49 $$

Het kwadraat van de standaarddeviatie wordt de variantie (Var(x)) genoemd. Doordat dit kwadraat de wortel uit de definitie van de standaard deviatie haalt, kunnen we hier vaak iets gemakkelijker mee rekenen:

$$ var(x) = \frac{1}{N} \sum_{i=0}^N (x_i - \mu)^2 $$

In deze definitie van de standaard deviatie en variantie hebben we gebruik gemaakt van het gemiddelde van de gehele populatie μ. Als we gebruik maken van het steekproefgemiddelde x̄, dan noemen we de standaard deviatie s. De formule voor de variantie wordt in dat geval net iets anders:

$$ s = \sqrt{\frac{1}{N-1} \sum_{i=0}^N (x_i - \bar{x})^2} $$

Het verschil zit hem in de (N-1). Dit wordt Bessel's correctie genoemd. Aan het einde van de paragraaf gaan we afleiden waar deze verandering vandaan komt.

Toepassing: IQ en school prestaties

De gemiddelde cijfers van meiden op zowel de lagere school, de middelbare school en het hoger onderwijs zijn hoger dan die van jongens en dit terwijl het gemiddelde IQ van jongens en meisjes zo goed als gelijk is. Dit betekent dat meiden naast IQ andere kwaliteiten hebben die ze beter inzetten dan jongens. Met name werken zijn ze meer gedisciplineerd en geordend in hun werk.

Hoewel het gemiddelde IQ van mannen en vrouwen zo goed als gelijk is (100), is de standaard deviatie van het IQ dat niet. Dit blijkt voor mannen iets hoger te liggen (ongeveer 15) dan bij vrouwen (ongeveer 14). Dit betekent dat er gemiddeld gezien meer mannen zijn met een extreem laag IQ en meer mannen met een extreem hoog IQ. In twee studies van 11-jarige Schotse kinderen werd een ratio van 1:2 gevonden tussen jongens en meisjes bij een IQ van 140 en bij een IQ van 60. Vele andere studies hebben eenzelfde resultaat gevonden.

Bron: Sex Differences in Variability in General Intelligence, by Johnson, Carothers & Deary (Perspectives on Psychological Science, 2008)

Rekenen met de variantie

In de paragraaf hebben we gelezen dat de variantie te schrijven is als:
$$ var(x) = \frac{1}{N} \sum_{i=0}^N (x_i - \mu)^2 $$
In termen van de verwachtingswaarde kunnen we dit beknopter opschrijven als:
$$ var(x_i) = E[ (x_i - E[x_i])^2 ] $$
Als we de haakjes uitwerken, dan vinden we:
$$ var(x) = E[x^2 - 2xE[x] + E[x]^2 ] $$
Omdat het gemiddelde van het gemiddelde (E[E[x]]) weer gewoon het gemiddelde oplevert (E[x]), kunnen we dit verder versimpelen tot:
$$ var(x) = E[x^2] - 2E[x]E[x] + E[x]^2 $$ $$ var(X) = E[X^2] - E[X]^2 $$
Dit is een andere veelgebruikte formule voor de variantie.

We kunnen hiermee een aantal rekenregels vinden voor het rekenen met variantie. In dit hoofdstuk gaan we een aantal keer de variantie van x/N nodig hebben. Laten we eens kijken hoe we dit kunnen schrijven:
$$ var \left( \frac{x}{N} \right) = E\left[ \frac{x^2}{N^2} \right] - E\left[ \frac{x}{N} \right]^2 $$
Dit kunnen we versimpelen tot:
$$ var \left( \frac{x}{N} \right) = \frac{1}{N^2} (E[X^2] - E[X]^2) $$
De uitspraak tussen haakjes aan de rechterzijde is gelijk aan var(x). Er geldt dus:
$$ var \left( \frac{x}{N} \right) = \frac{1}{N^2} var(x) $$
Ook gaan we de varantie van de optelling van twee variabelen nodig hebben:
$$ var(x_1 + x_2) = E[(x_1+x_2)^2] - E[x_1+x_2]^2 $$ $$ var(x_1 + x_2) = E[x_1^2+x_2^2+2x_1x_2] - (E[x_1]+E[x_2])^2 $$ $$ var(x_1 + x_2) = E[x_1^2]+E[x_2^2]+2E[x_1x_2] - E[x_1]^2 - E[x_2]^2 -2E[x_1]E[x_2] $$
De eerste en de vierde term vormen samen var(x₁) en de tweede en de vijfde term vormen var(x₂). We kunnen dus schrijven:
$$ var(x_1 + x_2) = var(x_1) + var(x_2) + 2(E[x_1x_2] - E[x_1]E[x_2]) $$
De term tussen haakjes zullen we vaker tegen komen. We noemen dit de covariantie (cov(x)). We vinden dus:
$$ var(x_1 + x_2) = var(x_1) + var(x_2) + 2cov(x_1,x_2) $$
We kunnen eenzelfde afleiding uitvoeren voor de variantie van x₁ - x₂. In dat geval vinden we:
$$ var(x_1 - x_2) = var(x_1) + var(x_2) - 2cov(x_1,x_2) $$
Later zullen zien dat de covariantie nul is als de variabelen x₁ en x₂ onafhankelijk van elkaar zijn. Dit betekent dat de ene meting x₁ geen invloed heeft op een andere meting x₂. Stel dat we bijvoorbeeld een aantal mensen willekeurig selecteren uit een populatie en daar de lengte van meten, dan heeft meting 1 geen invloed op meting 2 (als je alle metingen uit één familie zou halen, dan zouden de metingen niet afhankelijk zijn, omdat de familie meer genetische overeenkomsten heeft dan willekeurige individuen in de bevolking).

Met de rekenregels die we tot dusver hebben gevonden ook een formule vinden voor de variantie van x̄.
$$ var(\bar{x}) = var\left( \frac{x_1 + x_2 + ... + x_i}{N} \right) = \frac{1}{N^2} var(x_1 + x_2 + ... + x_i) $$
Als de variabelen x_i allemaal onafhankelijke metingen zijn, dan wordt de covariantie nul en kunnen we dit herschrijven als:
$$ var(\bar{x}) = \frac{1}{N^2} (var(x_1) + var(x_2) + ... + var(x_i)) $$
Voor elke meting x_i doen we een meting aan dezelfde populatie. Als gevolg is de variantie van alle metingen gelijk. We kunnen dit dus schrijven als:
$$ var(\bar{x}) = \frac{1}{N^2} N var(x) = \frac{var(x)}{N} $$

Afleiding van Bessel's correctie

In het hoofdstuk hebben we gelezen dat de standaard deviatie bij een steekproef met gemiddelde x̄ gegeven wordt door:
$$ s = \sqrt{\frac{1}{N-1} \sum (x_i - \bar{x})^2} $$
Om te zien dat dit de juiste uitdrukking is, gaan we eerst aannemen dat de volgende uitdrukking voor de standaard deviatie geldt:
$$ s_N = \sqrt{\frac{1}{N} \sum (x_i - \bar{x})^2} $$
Om te zien dat dit niet werkt gaan we de verwachtingswaarde uitrekenen van σ² - s_N²:
$$ E[\sigma^2 - s_N^2] = E\left[ \frac{1}{N} \sum (x_i - \mu)^2 - \sum (x_i - \bar{x})^2 \right] $$
Als we de rechterzijde buiten haakjes halen, dan vinden we:
$$ E[\sigma^2 - s_N^2] = E\left[ \frac{1}{N} \sum (\mu^2 - \bar{x}^2 + 2x_i(\bar{x}-\mu)) \right] $$ $$ E[\sigma^2 - s_N^2] = E\left[ \mu^2 - \bar{x}^2 + 2\bar{x}(\bar{x}-\mu)) \right] $$
Dit kunnen we verder versimpelen tot:
$$ E[\sigma^2 - s_N^2] = E\left[ \mu^2 - 2\bar{x} \mu + \bar{x}^2 \right] $$ $$ E[\sigma^2 - s_N^2] = E\left[ (\bar{x} - \mu)^2 \right] $$ $$ E[\sigma^2 - s_N^2] = var(\bar{x}) $$
In het vorige extra stukje gevonden dat we var(x̄) kunnen herschrijven tot:
$$ E[\sigma^2 - s_N^2] = \frac{var(x)}{N} = \frac{\sigma^2}{N} $$
Als we dit omschrijven, dan vinden we:
$$ E[s_N^2] = \sigma^2 - \frac{\sigma^2}{N} = \frac{N-1}{N}\sigma^2 $$
We verwachtingswaarde van s_N² is dus niet gelijk aan de verwachtingswaarde van σ². Als gevolg kunnen we concluderen dat s_N² geen goede benadering is van σ². We kunnen dit oplossen door s_N² te vermenigvuldigen met N/(N-1):
$$ s^2 = \frac{N}{N-1}s_N^2 $$
Als we de definitie van s_N uitwerken, dan vinden we:
$$ s^2 = \frac{1}{N-1}\sum (x_i - \bar{x})^2 $$

De normale verderling

Stel dat we 30 keer achter elkaar een dobbelsteen gooien en de waarden bij elkaar optellen. En stel dat we daarna dit experiment 10.000 keer herhalen. We vinden dan het onderstaande resultaat. Op de horizontal as staat afgebeeld de totale waarde van de 30 worpen en op de verticale as vinden we hoeveel elk van de totale waarden voor zijn gekomen (dit wordt ook wel de frequentie genoemd).

Hoe vaker je het experiment herhaalt, hoe meer onze distributie een vorm nadert die we de normale verdeling noemen. In dat geval schrijven we op de verticale as alleen niet de frequentie, maar de kans (P(x)) op het deeltje op positie x aan te treffen. Deze verdeling blijkt te beschrijven met de volgende formule:

$$ P(x) = \frac{1}{\sigma \sqrt{2 \pi}} \exp \left[ -\frac{1}{2}\left( \frac{x-\mu}{\sigma} \right)^2 \right] $$

In het onderstaande programma kan je de normale verdeling zien bij verschillende μ en σ.

De term tussen de ronde haakjes in de formule noemen we ook wel de z-waarde. Er geldt dus:

$$ z = \frac{x - \mu}{\sigma} $$

We kunnen de formule voor de normale verdeling dus ook schrijven als:

$$ P(x) = \frac{1}{\sigma \sqrt{2 \pi}} \exp \left[ -\frac{1}{2}z^2 \right] $$

Omdat we hier te maken hebben met een continue grafiek, is de kans op één specifieke waarde van x echter (zo goed als) nul. Als we een kans willen vinden boven de nul, dan moeten we de kansen voor een hele reeks waarden x bij elkaar optellen. Anders gezegd, we moeten het oppervlak onder de grafiek bepalen.

Als je het totale oppervlak onder de grafiek bepaalt, dan moet je noodzakelijk 1 (100%) vinden, want de kans dat het deeltje een waarde heeft tussen min oneindig en oneindig is natuurlijk 100%. Hiervoor is gezorgd door de factor die voor de exponent in de formule staat (hoe men op deze waarde is gekomen gaan we hier niet bespreken).

Als we het oppervlak van min oneindig tot het punt x_i willen berekenen, dan moeten we integreren over dit bereik:

$$ P(x \lt x_i) = \frac{1}{\sigma \sqrt{2 \pi}} \int_{-\infty}^{x_i} \exp \left[ -\frac{1}{2}\left( \frac{x-\mu}{\sigma} \right)^2 \right] dx $$

Het blijkt dat deze vergelijking te herschrijven is tot:

$$ P(x \lt x_i) = \frac{1}{2} \left[ 1 + \text{erf} \left( \frac{x_i-\mu}{\sigma \sqrt{2}} \right) \right] $$

Of in termen van de z-waarde:

$$ P(x \lt x_i) = \frac{1}{2} \left[ 1 + \text{erf} \left( \frac{z}{\sqrt{2}} \right) \right] $$

De functie erf is hier de zogenaamde error functie. Het fijne is dat deze functie door sommige rekenmachines (inclusief de rekenmachine in google) herkent wordt.

Als we het oppervlak van x = x_i tot x = oneindig willen bepalen, dan rekenen we eerst het oppervlak van x = -oneindig tot x = A uit en dan doen we 1 (100%) min deze waarde:

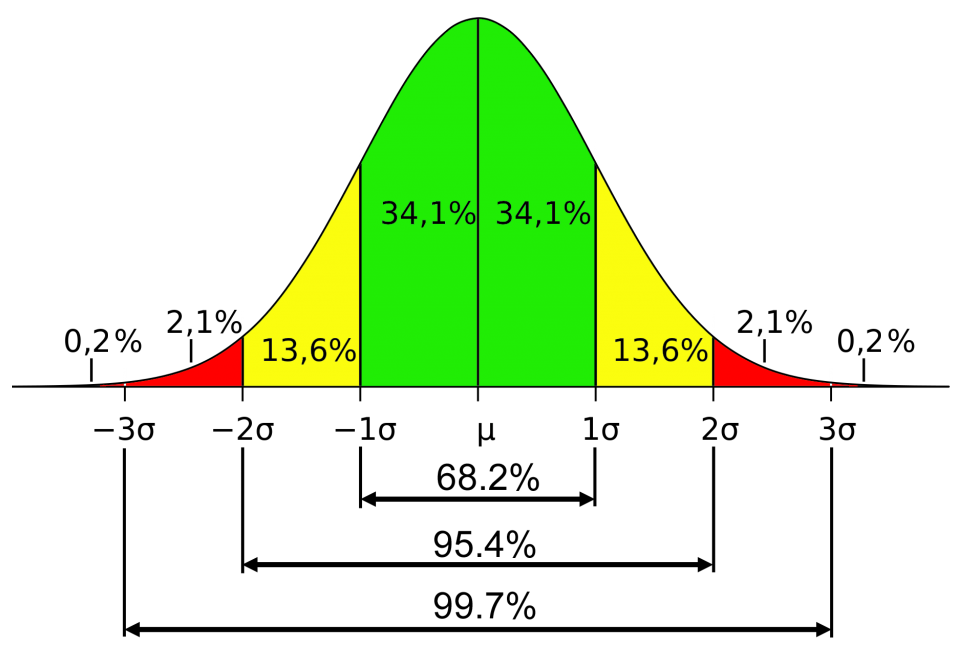
$$ P(x \gt x_i) = 1 - \frac{1}{2} \left[ 1 + \text{erf} \left( \frac{x_i-\mu}{\sigma \sqrt{2}} \right) \right] $$

In de onderstaande afbeelding zijn een aantal percentages uitgerekend. Zoals je ziet bevindt 34,1 × 2 = 68,2% van de verdeling zich binnen 1 standaard deviatie van het gemiddelde. De kans dat een meetwaarde een standaard deviatie boven het gemiddelde zit is 13,6 + 2,1 + 0,2 = 15,9%. De kans dat het twee standaard deviaties boven het gemiddelde zit is slechts 2,1 + 0,2 = 2,3%.

Toepassing: Hoe lang gaat een wasmachine mee?

Stel dat een wasmachine gemiddeld 5000 uur gebruikt kan worden voordat deze kapot gaat, met een standaard deviatie van 500 uur. Bereken welk percentage aan wasmachines na 5800 uur nog werkt.

We doen hiervoor 1 min de de kans uit dat de wasmachine minder dan 5800 uur zal werken:
$$ P(x \gt A) = 1 - \frac{1}{2} \left[ 1 + \text{erf} \left( \frac{A-\mu}{\sigma \sqrt{2}} \right) \right] $$ $$ P(x \gt 5800) = 1 - \frac{1}{2} \left[ 1 + \text{erf} \left( \frac{5800-5000}{500 \sqrt{2}} \right) \right] = 5,5 $$

Toepassing: Studie naar exceptionele mensen

Bij onderzoeken naar de bevolking hebben we vaak te maken met normale verdelingen. Neem bijvoorbeeld het onderzoek naar hoe gelukkig mensen zich voelen. Zoals we net gezien hebben, zullen de meeste mensen rond het gemiddelde zitten. Zo'n 68,2% zal minder dan een standaard deviatie van het gemiddelde verwijderd zijn en zo'n 95,4% is minder dan twee standaard deviaties van het gemiddelde verwijderd. Als gevolg krijg je dat bij onderzoeken naar de gehele bevolking de uitersten in beide richtingen amper een rol spelen (slechts 4,6% zit verder dan twee standaard deviaties van het gemiddelde).

Toch kan onderzoek naar deze kleine groep extreem gelukkige en extreem ongelukkige mensen heel waardevol zijn. Alleen als we deze groepen appart bestuderen, kunnen we erachter komen wat deze groepen anders doen. Wellicht kunnen we van het gedrag van de extreem gelukkige mensen iets leren en wellicht heeft het zin om uniek gedrag van de extreem ongelukkige mensen af te leren.

Omdat deze twee groepen klein zijn, is het lastig om grote (en dus betrouwbare) studies naar deze groepen uit te voeren. Toch wordt dit de laatste decennia steeds vaker gedaan. Zo blijkt bijvoorbeeld dat de meest gelukkige 10% van de bevolking een rijk sociaal leven heeft, met zowel meer oppervlakkige als goede vrieden. We hebben ook vaak veel sociale support binnen hun netwerk. Tevens bleek dat deze groep mensen niet minder tegenslagen te verduren had dan de rest van de bevolking en ze hadden ook niet meer rijkdom.

Bron: Very happy people, by Seligman & Diener ( Psychological Science, 2002)

Toepassing: De golffunctie van een elektron

Volgens de kwantummechanica zijn kleine deeltjes zoals elektronen te beschrijven als klein golfje. Als we de positie en de snelheid van een elektron zo nauwkeurig mogelijk weten, dan wordt dit golfje beschreven door de volgende golffucntie:
$$ \psi = \sqrt{\frac{1}{\sigma \sqrt{2\pi}}} \exp{\left[ -\frac{1}{4}\frac{(x-\mu)^2}{\sigma^2} \right]} $$
Volgens de kwantummechanica geeft het kwadraat van de golffunctie de kansverdeling om het elektron op een bepaalde positie (x) aan te treffen. Dit wordt:
$$ P(x) = \psi^2 = \frac{1}{\sigma \sqrt{2\pi}} \exp{\left[ -\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2} \right]} $$
Dit is een normale verdeling!

Volgens de kwantummechanica moet elk deeltje ook voldoen aan de zogenaamde onzekerheidsrelatie. Deze wordt gegeven door:
$$ \sigma_x\sigma_p \geq \frac{\hbar}{2} $$
p is hier de impuls (p) van het deeltje en dit is gelijk aan de massa keer de snelheid (p = mv). Als we de positie en de snelheid van het elektron zo nauwkeurig mogelijk weten dat zijn beide kanten van de onzekerheidsrelatie aan elkaar gelijk. Als we de positie en de snelheid minder nauwkeurig weten, dan is de linker zijde groter.

Uit de kwantummechanica blijkt tevens dat in dit geval de standaarddeviatie van de impuls gelijk is aan:
$$ \sigma_p = \frac{\hbar}{2\sigma_x} $$
Als we dit invullen in de onzekerheidsrelatie, dan vinden we:
$$ \sigma_x\sigma_p = \sigma_x \times \frac{\hbar}{2\sigma_x} = \frac{\hbar}{2} $$
De normale verdeling blijkt dus overeen te komen met de meest nauwkeurige meting van het elektron.

De p-waarde en significantie

In deze paragraaf gaan we leren aantonen of interventies een meetbaar effect hebben. Tijd voor een rekenvoorbeeld. Een docent wilt meten of het meegeven van een oefentoets een positief effect heeft op de cijfers van de toets. In voorgaande jaren hebben de leerlingen van zijn school gemiddeld een 6,5 gehaald voor een toets met een standaard deviatie van 0,5. De docent geeft dit jaar aan één willekeurige leerling een oefentoets mee en deze leerling blijkt een 7,0 te halen voor de toets. Dit is standaard deviatie hoger dan het gemiddelde.

Betekent dit dat de interventie gewerkt heeft? Hoewel dit cijfer boven het gemiddelde ligt, kan het natuurlijk ook gewoon toeval zijn dat deze leerling een hoog cijfer haalde. Misschien was deze leerling toevallig bovengemiddeld intelligent of had hij harder dan gemiddeld geleerd. Om dit probleem op te lossen kunnen we uitrekenen wat de kans is dat dit hoge cijfer gewoon toeval was. We noemen dit de zogenaamde p-waarde. We vinden in dit geval:

$$ P(x \gt x_i) = 1 - \frac{1}{2} \left[ 1 + \text{erf} \left( \frac{x_i-\mu}{\sigma \sqrt{2}} \right) \right] $$ $$ P(x \gt 7) = 1 - \frac{1}{2} \left[ 1 + \text{erf} \left( \frac{7-6,5}{0,5 \sqrt{2}} \right)\right] = 0,159 $$

De p-waarde is dus 0,159 en dus is er 15,9% kans dat het cijfer toeval was. We zeggen ook wel dat er 15,9% kans is dat de nulhypothese correct is. Dit is de hypothese die stelt dat de interventie geen effect heeft.

Maar wat nu als hij de oefentoets aan 30 leerlingen meegeeft en deze leerlingen gemiddeld een 7,0 halen? In dat geval moeten we weten wat de kans is dat een groep van 30 leerlingen een 7,0 haalt. We moeten hiervoor in onze verbeelding een normale verdeling maken van vele groepen van 30 leerlingen. Stel dat de nulhypothese correct is, dan zal over het algemeen het gemiddelde van 30 leerlingen dichter bij het gemiddelde liggen dan een gemiddelde van één leerling. Dit komt omdat de cijfers van de 30 leerlingen elkaar met hoge waarschijnlijkheid zullen uitmiddelen (een 6,0 en een 7,0 zullen het gemiddelde bijvoorbeeld weer terugbrengen op een 6,5). Als gevolg verwachten we dat de standaard deviatie van een groep van 30 leerlingen kleiner is. Aan het eind van de paragraaf gaan we bewijzen dat:

$$ \sigma_{sample} = \frac{\sigma}{\sqrt{N}} $$

We noemen deze gecorrigeerde standaard deviatie de standaard error.

De z-waarde wordt in dat geval:

$$ z = \frac{\bar{x} - \mu}{\sigma_{sample} } = \frac{\bar{x} - \mu}{\sigma / \sqrt{N}} $$

In ons voorbeeld vinden we:

$$ z = \frac{7 - 6,5}{0,5 / \sqrt{30}} = 5,48 $$

De p-waarde voor dit sample wordt hiermee:

$$ P(x \gt x_i) = 1 - \frac{1}{2} \left[ 1 + \text{erf} \left( \frac{z}{\sqrt{2}} \right) \right] $$ $$ P(x \gt 7) = 1 - \frac{1}{2} \left[ 1 + \text{erf} \left( \frac{5,48}{\sqrt{2}} \right) \right] = 2,2 \times 10^{-8} $$

De p-waarde is nu zo klein dat het resultaat de kans zoe goed als nul is dat het resultaat een toevalstreffer is. We kunnen ook uitrekenen hoeveel metingen we zouden moeten doen om dit resultaat bij toeval te vinden. Dit is gelijk aan 1/p-waarde:

$$ \frac{1}{2,2 \times 10^{-8}} = 4,5 \times 10^7 \times $$

We verwachten dit resultaat dus slechts 1 op de 4,5 × 10⁷ keer bij toeval.

Als de p-waarde klein genoeg is, dan kunnen we de nulhypothese verwerpen en de nieuwe hypothese kunnen aannemen. Maar wanneer is de p-waarde klein genoeg? Over het algemeen wordt geaccepteerd dat een waarde on der de p = 0,05 (5%), of nog beter, onder de p = 0,01 (1%) klein genoeg is. We spreken in dat geval van een significant resultaat.

De p-waarde is van groot belang om een inschatting te maken of je meetgegevens echt iets betekenen of dat het om toevalstreffers gaat. Hoe lager de p-waarde, hoe betrouwbaarder het resultaat. De p-waarde zegt echter niks over hoe groot het effect is dat gemeten is. Het kan bijvoorbeeld voorkomen dat een meting extreem betrouwbaar is (lage p-waarde), maar dat het effect van de meting zeer klein is en het dus weinig nut heeft om de verandering door te voeren.

Let er wel op dat de p-waarde alleen geldig is als de rest van het experiment goed is uitgevoerd. Als de leerlingen bijvoorbeeld niet willekeurig gekozen zijn, maar in plaats daarvan zich vrijwillig hebben aangemeld, dan is de kans groot dat dit nu juist leerlingen zijn die bovengemiddeld scoren. Of wellicht blijft het niet de oefentoets te zijn die voor het hoge cijfer heeft gezorgd, maar het feit dat de leerling zich extra gesteund voelde door als enige de oefentoets mee naar huis te krijgen, hetgeen hem gemotiveerder maakte om te leren. Al deze problemen moeten zo veel mogelijk vermeden worden.

Toepassing: Waarom de meeste studies onjuist zijn

In een artikel uit 2005 van John Ioannidis genaamd Why Most Published Research Findings are False werd beschreven dat de meerderheid van de gepubliceerde studies in de sociale wetenschappen niet te reproduceren was. Dit betekent dat wanneer het onderzoek nogmaal herhaalt werd, dat niet nogmaals een vergelijkbaar resultaat gevonden werd. Dit wordt het replicatieprobleem genoemd.

Hoe kan dit? Hebben de schrijvers van deze artikelen niet netjes hun p-waardes bepaald? Dit hebben ze natuurlijk wel gedaan! Er zijn echter een aantal andere problemen die onderzoeken onzeker maken, zelfs met correcte p-waarde. Ten eerste is de publicatie in een belangrijk wetenschappelijk tijdschrift erg competatief. Als je gepubliceerd wilt worden, dan moet je studie opvallen, maar dit incentiveert onderzoekers om hun data iets beter te presenteren dan in werkelijkheid het geval is. Tevens is de kans aanwezig dat een onderzoek een heel onverwacht resultaat heeft juist omdat deze onwaar is.

Ook is er een effect dat het file-drawer problem wordt genoemd. Dit werkt als volgt. Stel dat een onderzoeker een fenomeen meet en een p-waarde van 0,05 vindt. Dit betekent dat er slechts 1 op de 20 kans is dat we hier met een toevalstreffer te maken hebben. Stel echter dat 19 andere mensen dit experiment ook gedaan hebben en een p-waarde vinden die niet significant is, maar dit onderzoek niet publiceren vanwege het tegenvallende resultaat. Deze 19 onderzoeken komen dus in een la terecht (een "file drawer"). In dat geval zou je met alle onderzoeken samen moeten concluderen dat het positieve resultaat inderdaad een toevalstreffer was. Helaas kom je hier echter niet achter als deze onderzoeken nooit boven tafel komen.

Een ander probleem ontstaat als mensen selectief op zoek gaan naar data die hun hypothese ondersteunt. Dit gebeurt vaak bij conspiracy theories. Neem bijvoorbeeld de aanslag op de Twin Towers in New York. Duizenden mensen hebben langdurig naar patronen gezorgd in de data om meer te weten te komen over wat er die dag gebeurt. Stel dat iemand vindt dat een aantal bedrijven de dag voor de aanslag net een verzekering hadden afgesloten en tijdens de aanslag niet op werk verschenen. Dit lijkt dubieus. Wisten deze mensen van de aanslag? Ten eerste kan het natuurlijk zijn dat er elke dag verzekeringen worden afgesloten in een gebouw waar 2000 mensen werkten. Maar stel dat de gebeurtenis toch bijzonder was en een p-waarde van 0,01 had. Dit betekent dat je 99% kans hebt dat het hier niet om toeval gaat! Toch ligt het niet zo simpel. Stel dat er nog 99 andere patronen in de data werden gezocht, maar deze niet werden gevonden, dan zou je theoretisch zelfs verwachten dat er een keer een toevalstreffer van 0,01 voorbij komt. Als je de data op deze manier bekijkt, kan het bizarste toeval soms compleet in de lijn der verwachtingen zijn.

Door al deze problemen komen er steeds meer wetenschappers die niet alleen waarde hechten aan een significante p-waarde, maar die ook kijken naar de grootte van het effect. Hoe groter een effect namelijk is, hoe gemakkelijker het te meten en te reproduceren is. Dit wordt het onderwerp van de volgende paragraaf.

Toepassing: z-distributies en t-distributies

De verdeling die we tot dusver besproken hebben gaat uit van een normale verdeling. We noemen dit ook wel de z-distributie. Voor kleine samples van onder de 30 is het echter nauwkeuriger om van de t-distributie gebruikt te maken. Bij de t-distributie hoort een t-score:
$$ t = \frac{\bar{x} - \mu}{s} $$
Zoals je ziet wordt hier gedeeld niet door de standaard deviatie van de populatie, maar door de standaard deviatie van je steekproef (let op dat dit niet hetzelfde is als σ_sample. s is de standaard deviatie van de individuele metingen die gedaan zijn ten opzicht van het gemiddelde van die metingen. σ_sample is de standaard deviatie van een heel aantal metingen tegelijk).

Net als bij de z-distributie kunnen we de bijbehorende kans berekenen met behulp van het oppervlak onder de t-distributie. De formule hiervoor is iets complexer en als gevolg wordt dit vaak met een computerprogramma uitgerekend (type "t-score calculator" in google en je vindt allerlei programma's waarmee je dit kan doen). Om de kans te bepalen is behalve de t-waarde ook nog het aantal vrijheidsgraden (DF, van "degrees of freedom") nodig. Er geldt:
$$ DF = N - 1 $$
Misschien dat je je afvraagt waarom de t-distributie een andere vorm heeft dan de z-distributie. Dat heeft met het volgende te maken. Door de vorm van de normale verdeling, liggen de meeste meetpunten rond het gemiddelde. Ook kunnen we aan de definitie zien dat de variantie van punten die verder liggen veel groter is. Als gevolg hebben de meeste meetpunten een variantie die kleiner is dan het gemiddelde (een paar grote varianties meetpunten wegen op tegen een hoop kleine varianties). Als gevolg hiervan hebben we bij een klein sample er veel kans dat we waarden vinden met een ondergemiddelde variantie. De variantie zal hierdoor iets kleiner worden dat in werkelijkheid het geval zal zijn en als gevolg zou je een te kleine z-waarde krijgen. Om hiervoor te corrigeren maken we gebruik van de t-waarde (de t-distributie iets breder gemaakt).

Bij een sample van 30 of meer metingen verdwijnt het verschil tussen de z-waarde en de t-waarde. In dat geval is het handiger om gebruik te maken van de z-distributie.

Afleiding

In dit stukje gaan we bewijzen dat:
$$ \sigma_{sample} = \frac{\sigma}{\sqrt{N}} $$
Stel we hebben een sample met grootte N uit een grotere populatie die normaal verdeeld is. Het gemiddelde van dit sample wordt dan gegeven door:
$$ \bar{x} = \frac{(x_1 + x_2 + ... + x_n)}{N} $$
In de eerste paragraaf hebben we laten zien dat:
$$ var (\bar{x}) = \frac{var(x)}{N} $$
Als we aan beide kanten de wortel trekken, dan vinden we de bijbehorende standaarddeviatie:
$$ \sigma_{sample} = \frac{\sigma}{\sqrt{N}} $$

De effectgrootte

In deze paragraaf gaan we leren de effectgrootte te berekenen van een bepaalde interventie. Stel dat een klas normaalgesproken voor een bepaalde toets een 6,0 haalt, maar dat na een bepaalde interventie het cijfer gemiddeld een 7,0 is geworden. De effectgrootte is dan gelijk aan:

$$ 7,0 - 6,0 = 1,0 \text{ punt}$$

We hebben hier gekeken naar het absolute verschil tussen de cijfers van de twee groepen. In sommige situaties is dit echter geen handige maat voor de effectgrootte. Stel dat men bijvoorbeeld een interventie uitvoert met als doen om mensen meer zelfvertrouwen te geven. De mate van zelfvertrouwen kan bijvoorbeeld gemeten worden met behulp van een enquete. Aan de hand van de antwoorden kan dan een getal gekoppeld worden aan hoeveel zelfvertrouwen een persoon heeft. Stel dat door interventie het zelfvertrouwen is gestegen van 60 naar 64. Wat zegt dit ons nu echt? Het is in dit geval beter om het verschil tussen deze waarden te delen door de standaard deviatie. We berekenen dan hoeveel standaard deviaties er tussen deze twee waarden passen. We noemen deze vorm van de effectgrootte Cohen's d:

$$ \text{Cohen's d} = \frac{\bar{x}_{interventie} - \mu}{\sigma} $$

Ruwweg wordt vaak gezegd dat d = 0,2 een klein effect is. De normale verdeling is hier immers maar 20% van een standaard deviatie verschoven. Bij p = 0,5 wordt het effect middelmatig en vanaf d = 0,8 spreken we van een groot effect.

Stel we vinden een effectgrootte van 1,0. Dit betekent dat de verdeling 1,0 standaard deviatie is opgeschoven. Als we willen weten hoeveel procent van de nieuwe verdeling boven het gemiddelde van de oude verdeling komt, dan gebruiken we wederom het oppervlak onder de normale verdeling:

$$ P(x \lt \bar{x}_{interventie}) = \frac{1}{2} \left[ 1 + \text{erf} \left( \frac{\bar{x}_{interventie} - \mu}{ \sigma \sqrt{2}} \right) \right] $$ $$ P(x \lt \bar{x}_{interventie}) = \frac{1}{2} \left[ 1 + \text{erf} \left( \frac{d}{ \sqrt{2}} \right) \right] $$ $$ P(x \lt \bar{x}_{interventie}) = \frac{1}{2} \left[ 1 + \text{erf} \left( \frac{\text{1,0}}{ \sqrt{2}} \right) \right] = 0,841 $$

In het onderstaande programma is dit percentage telkens uitgerekend bij verschillende effectgroottes.

Het is belangrijk het verschil tussen p-waarden en effectgroottes goed te kennen. De p-waarde geeft aan hoe betrouwbaar je data is. Hoe kleiner de p-waarde, hoe betrouwbaarder je resultaat. De effectgrootte daarentegen geeft aan hoe sterk het effect van de interventie is. Een onderzoek kan bijvoorbeeld een hele kleine p-waarde hebben (en dus zeer betrouwbaar zijn), maar slechts een kleine effectgrootte hebben (dus het doet zo goed als niks). Een bekend voorbeeld is het effect van klasgrootte op cijfers op school. Deze relatie is enorm statistisch signficant (mede door de enorme hoeveelheid data die we hierover hebben), maar het effect is onmerkbaar klein. Het argument dat kleinere klassen de cijfers verhoogt deugt dus niet (het verlaagd de werkdruk van de docent natuurlijk wel).

Toepassing: cognitieve gedragstherapie

Cognitieve gedragstherapie (CBT) is de best geteste psychologische interventie waarmee mensen geholpen kunnen worden als ze last hebben van bijvoorbeeld paniekaanvallen of depressie. Een recent onderzoek, waarbij de data van een hele reeks studies werd gecombineerd vond een effectgrootte van 0,75 voor zware depressie (p < 0,001) en 0,81 voor paniekaanvallen (p < 0,001).

De groep werd vergeleken met een groep die geen therapie kreeg. Deze groep werd verteld dat ze op een wachtlijst stonden. In dat geval was het effect d = 0,98 (p = 0,002). Dit is dus het effect van de therapie in vergelijking tot niets doen. Het is ook interessant om het effect van CBT te vergelijken met de therapie die mensen al kregen ("care as usual"). In dat geval was het effect natuurlijk lager, maar nog steeds 0,60 (p < 0,001).

We zien ook een bijzonder resultaat als we CBT vergelijken met een placebo (een nepmedicijn). In dat geval was de effectgrootte van CBT 0,55 (p < 0,001). Schokkend genoeg blijkt in deze studie het placebo dus beter te werken dan de gemiddelde therapie die mensen normaalgesproken ontvangen.

Bron: How effective are cognitive behavior therapies for major depression and anxiety disorders? A meta-analytic update of the evidence, door Cuijpers, Cristea, et al. (World Psychiatry, 2016)

Toepassing: Het effect van psilocybine

Recent onderzoek heeft het aannemelijk gemaakt dat verschillende drugs kunnen helpen bij het verbeteren van onze mentale gezondheid, zelfs bij problemen waar de huidige psychologie weinig raad weet. In een studie werd bijvoorbeeld gevonden dat cognitieve gedragstherapie in combinatie met psilocybine (de werkzame stof in paddo's) kan helpen bij stoppen met roken. Zelfs 12 maanden na afloop van de interventie was 67% nog steeds gestopt. Dit is enorm veel, want als mensen zonder hulp met roken willen stoppen, dan is slechts 10% succesvol. In een andere studie werd CBT gecombineerd met MDMA (de werkzame stof in ecstasy) bij de behandeling van posttraumatische stressstoornis met als resultaat een effectgrootte van d = 1,58.

In een ander onderzoek werd zelfs gevonden dat psilocybine de persoonlijkheid langdurig kunnen veranderen. Dit is opmerkelijk, omdat de persoonlijkheid bij volwassenen erg stabiel is. Het ging hier om de eigenschap openheid. Wetenschappers hebben in het verleden een betrouwbare vragenlijst weten op te stellen om openheid te meten. Hieruit komt dan een getal rollen. Voor deze groep lag het gemiddelde op 64. Na een aantal sessies met psilocybine bleek openheid gemiddeld met 2,8 punten gestegen. Als alleen gekeken werd naar mensen die aangaven een krachtige ervaring te hebben gehad, dan werd zelf 5,7 punten stijging gemeten (de andere deelnemers hadden geen toename in openheid). 14 maanden laten was van de groep met sterke ervaring nog steeds een stijging van 4,2 over. Het was dus een effect dat erg lang aanhield. Tevens gaven 60% van de deelnemers aan dit de ervaring in de top 5 stond van betekenisvolle ervaringen in hun leven.

Maar wat betekenen deze punten in openheid? Is 5,7 veel? Daarvoor moeten we de effectgrootte bepalen. Het blijkt dat de standaard deviatie van openheid rond de 10 ligt. Dit geeft ons een effectgrootte van ongeveer 5,7 / 10 = 0,6. Dit is dus een behoorlijk merkbare verhoging.

Dit zijn veelbelovende resultaten, maar deze onderzoeken zijn nog niet vaak herhaalt en zijn uitgevoerd met kleine groepen mensen. Het laatst genoemde onderzoek had bijvoorbeeld 52 deelnemers. Ook waren deze mensen niet willekeurig gekozen, maar waren het mensen die zichzelf hadden opgegeven. De kans is groot dat het hier dus gaat om mensen die al inherent interesse hadden in drugs. We kunnen uit deze onderzoeken dus nog geen harde conclusies trekken, maar toch zijn ze belangrijk, omdat ze andere wetenschappers aanzetten tot meer onderzoek.

Toepassing: de parapsychologie

Een aantal wetenschappers hebben op tientallen plekken op aarde zogenaamde random number generators (RNGs) neergezet. Deze apparaten genereren een reeks nullen en enen op basis van een kwantumfenomenen (zoals het verval van een radioactief deeltje), die volgens de algemeen geaccepteerde natuurkunde volledig op kans werken. De RNGs sturen per keer een optelling van 200 van deze nullen en enen op naar een server, waar de data kan worden bekeken (je kan de data vinden op deze website). Als de kans op een nul of een één inderdaad 50% is, dan vinden we gemiddeld een waarde van 200 × 0,5 = 100. Een dergelijke verdeling wordt een binomiale verdeling genoemd. De standaard deviatie van deze verdeling kunnen we uitrekenen met de volgende formule :
$$ \sigma = \sqrt{NP(1-P)} $$ $$ \sigma = \sqrt{200 \times 0,5(1-0,5)} = 7.07 $$
68,2% van de data (1 standaard deviatie van het gemiddelde) zal dus vallen tussen de 93 (100 - 7) en de 107 (100 + 7). Een waarde van boven de 121 (100 + 7 + 7 + 7) komt maar 0,2% voor.

Het doel van het experiment was om te kijken of de reeks getallen van de verschillende RNGs vaker gecorreleerd waren als er een heftige gebeurtenis plaatsvindt op aarde. Het idee was dat wellicht het gemeenschappelijke bewustzijn van mensen een invloed zou kunnen uitoefenen op deze processen (het is maar een zeer kleine minderheid van wetenschappers die hierin gelooft, maar het is wel een leuk experiment).

De volgende stap was dat wetenschappers op zoek gingen naar ingrijpende gebeurtenissen die een wereldwijde impact hadden. Hieronder zien we de correlatie tussen de data van 16 juni tot en met 20 september in het jaar 2001. Slechts eenmalig is in deze periode een waarde gemeten 3 standaard deviaties van het gemiddelde (zowel in negatieve als positieve richting). Bijzonder is dat dit net op 11 september gebeurt, de dag dat twee vliegtuigen het World Trade Center in vlogen.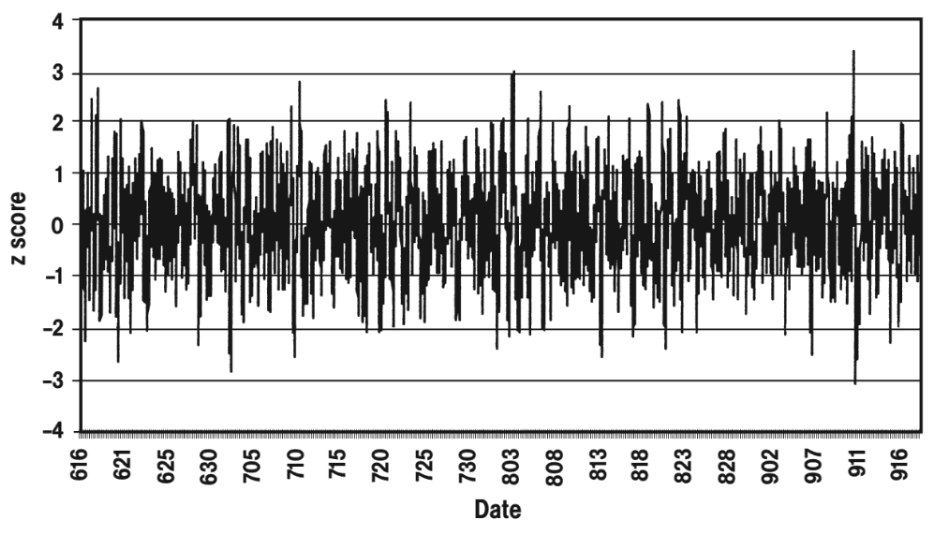

Andere wetenschappers hebben geprobeerd de conclusies van het onderzoek onderuit te halen. Zo wezen ze erop dat de correlatie twee uur voor de aanslag het grootst was, op een moment dat slechts een paar mensen ter wereld er nog van de plannen wisten. Ook merken ze op dat bij andere dramatische gebeurtenissen, zoals de start van de oorlog in Irak, geen verhoogde correlatie te meten is en dat op momenten dat er weinig aan de hand is, soms ook een hoge piek gemeten wordt. Ook bleek deze grafiek gemaakt te zijn door telkens naar de z-waarde te kijken van tijdspannen van 6 uur. De tweede bron die hieronder vermeld staat liet bijvoorbeeld zien dat als je tijdstappen neemt van 1 uur, het hele effect al weg valt. Het lijkt er dus op dat de 6 uur gekozen is juist omdat dit het beste resultaat gaf.

Toch blijft het uitzonderlijk dat we toch uit de data de bovenstaande grafiek hebben kunnen krijgen. We kunnen hier echter geen harde conclusies uit trekken, omdat het hier maar om één enkele meting gaat. Een dergelijke bijzonder claim zal pas algemeen worden geaccepteerd als dit effect vaak en consistent gemeten wordt.

Bron: Exploring relationships between random physical events and mass human attention, door Radin (Journal of Scientific Exploration, 2002)

En voor een kritische analyse:
Bron: Global Consciousness Project: An Independent Analysis of The 11 September 2001 Events, door May & Spottiswoode (self-published, 2002)

Correlatie

Als twee variabelen aan elkaar gerelateerd zijn, dan spreken we van een correlatie (r). Mensen die langer zijn, zijn bijvoorbeeld meestal ook zwaarder. Er is dus een correlatie tussen lengte en massa. Als de prijs van starterswoningen omhoog gaat, dan blijven jongeren langer bij hun ouders wonen. Er is dus een correlatie tussen de prijs van starterswoningen en hoe veel jaar jongeren thuis blijven.

In de onderstaande diagrammen zien we telkens een variabele x uitgezet tegen een variabele y. In het linker voorbeeld zien we een maximale correlatie. Voor elk meetpunt geldt hier dat bij elke waarde x een specifieke waarde y hoort. In het tweede en de derde afbeelding is dit niet het geval. Bij elke waarde x hoort hier een hele serie aan y waarden. De x determineert hier dus maar losjes de y-waarde. In de middelste afbeelding is helemaal geen correlatie tussen x en y. Bij de meest rechtse afbeelding is een inverse relatie te vinden. Hier geldt dat hoe groter x wordt, hoe kleiner y wordt.

Aan de correlatie wordt meestal een nummer gekoppeld tussen de -1 en de 1. We zien deze getallen boven de bovenstaande diagrammen staan. Bij een perfecte correlatie is deze waarde 1, zonder correlatie is deze waarde nul en bij een inverse correlatie is de correlatie -1.

We gaan nu op zoek naar een formule waarmee we de correlatie kunnen uitrekenen. In het onderstaande diagram zien we een aantal meetpunten. Ook is de gemiddelde waarde van x en de gemiddelde waarde van y aangegeven:

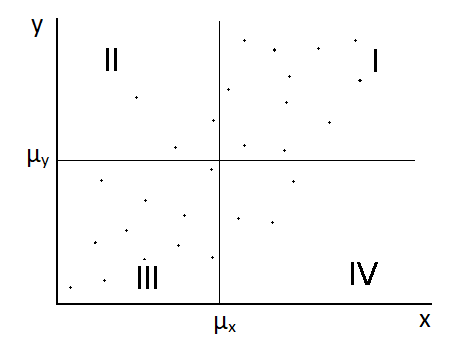
Om een formnule voor de correlatie te vinden definiëren we eerst de covariantie:

$$ cov(x,y) = \frac{1}{N}\sum{(x_i-\mu_x)(y_i-\mu_y)} $$

Aan het eind van de paragraaf zullen we aantonen dat deze definitie om te schrijven is naar de definitie voor de covariantie die we eerder in dit hoofdstuk gebruikt hebben.

In quadrant I van de bovenstaande afbeelding geldt dat de termen (x - μ_x) en (y - μ_y) positief zijn. In quadrant III zijn deze termen beide negatief. Als gevolg wordt (x - μ_x)(y - μ_y) in deze quadranten positief. In quadrant II en IV is deze waarde juist negatief. Bij een perfecte correlatie (1), zitten alle punten in quadrant I en III en is de covariantie dus positief. Bij een perfecte inverse correlatie (-1) zitten alle punten in quadrant II en IV en is de covariantie dus negatief. Merk ook op dat hoe verder de meetpunten afliggen van de gemiddelde waarden, hoe positiever (in deel I en III) en hoe negatiever (in deel II en IV) de covariantie wordt.

Uiteindelijk delen we de covariantie nog door σ_xσ_y. Dit zorgt ervoor dat de waarden netjes tussen de 1 en de -1 komen te liggen. We vinden dus:

$$ r = \frac{cov(x,y)}{\sigma_x\sigma_y} $$

Als we dit uitschrijven, dan vinden we:

$$ r = \frac{ \sum{(x_i-\mu_x)(y_i-\mu_y)} }{ \sqrt{ \sum (x_i - \mu_x)^2 \sum (y_i - \mu_y)^2 }} $$

In het onderstaande programma is deze formule gebruikt om de correlatie uit te rekenen bij verschillende meetwaarden:

Als we twee keer een meting doen aan dezelfde groep, dan krijgt de formule voor de correlatie een nog duidelijkere interpretatie. Neem het volgende voorbeeld. Stel dat wetenschappers een betrouwbare manier hebben gevonden om het zelfvertrouwen van mensen te meten. Het is dan een interessante vraag of dezelfde meting een tijd later een soortgelijk resultaat geeft. Dit zou namelijk betekenen dat zelfvertrouwen niet een vluchtige emotie is maar een lange-termijn persoonlijkheidseigenschap. Omdat persoonlijkheidseigenschappen nooit geheel constant blijven, is het een aannemelijke hypothese dat een deel van de variantie in zelfvertrouwen in de populatie constant blijft in de tijd en de rest zal schommelen. Het deel dat constant blijft noemen we T (staat voor "true") en het deel dat schommelt noemen we e (staat voor "error"). Voor elke meting x geldt dus:

$$ x = T + e $$

Bij dit soort testen is de standaard deviatie van beide metingen zo goed als gelijk (we meten immers twee keer aan dezelfde populatie). Er geldt dan dus σ_x = σ_y. De correlatie wordt hiermee:

$$ r = \frac{cov(x,y)}{\sigma_x\sigma_x} = \frac{cov(x,y)}{var(x)} $$

Aan het eind van de paragraaf gaan we laten zien dat de covariantie in deze formule gelijk is aan var(T). Dit is het deel van de variantie van zelfvertrouwen in de populatie dat constant is gebleven tussen de twee meetmomenten. De formule wordt dus:

$$ r = \frac{var(T)}{var(x)} $$

De correlatie geeft ons nu dus het deel van de variantie dat stabiel is gebleven in de tijd. Hieronder zien we het resultaat van deze meting met een week tussentijd. De correlatie blijkt hier gelijk aan 0,95. Dit betekent dat 95% van de variantie van zelfsvertrouwen in de populatie inderdaad toe te rekenen is aan een stabiele factor die met de test gemeten wordt.

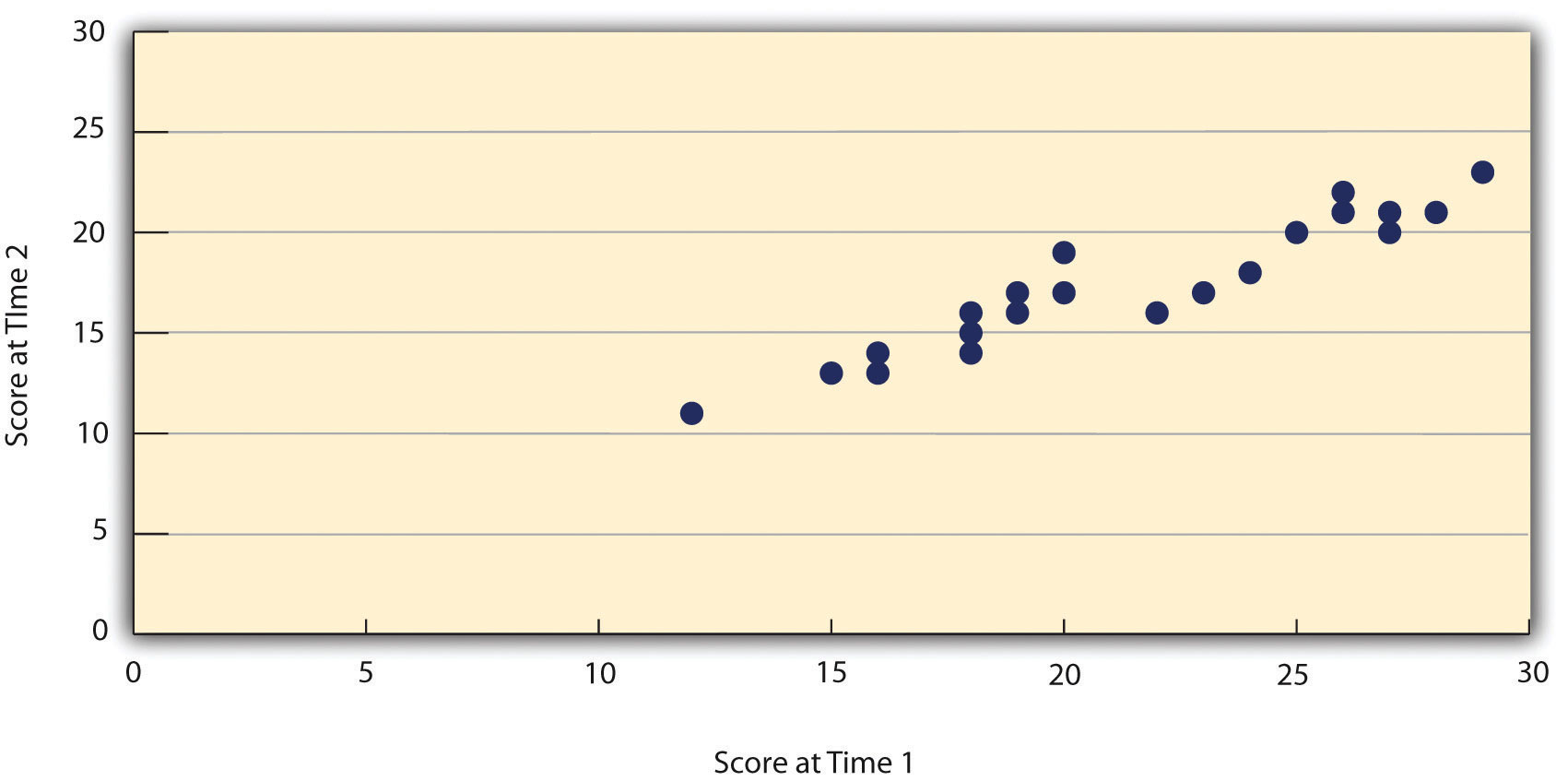
Bron: Research Methods in Psychology (Saylor Academy, 2012)
https://saylordotorg.github.io/text_research-methods-in-psychology/s09-02-reliability-and-validity-of-me.html

Toepassing: "Nature" of "nurture"

Met een aantal slimme experimenten is het de laatste decennia gelukt om te bepalen in hoeverre ons leven wordt gedetermineerd door onze genen ("nature"), welk deel door onze opvoeding ("nuture") en welk deel door onze eigen ervaringen. De resultaten van deze experiment zijn inmiddels al decennia zeer betrouwebaar (en ook zeer schokkend).

Laten we beginnen met ons gewicht. Om te kijken in hoeverre de variatie aan gewicht in onze populatie wordt veroorzaakt door genen, kunnen we het volgende experiment doen. Af en toe worden eeneiige tweelingen, ook wel monozygotische tweelingen (MZ) genoemd, bij geboorte ter adoptie opgegeven en komen beide kinderen in een ander gezin. MZ tweelingen hebben exact dezelfde genen. Stel dat zou blijken dat er een correlatie te vinden tussen de tweelingen van 1,0, zelfs als ze in een ander gezin zijn opgegroeid, dan zouden we moeten concluderen dat de genen volledig het gewicht bepaald hebben. Als we een correlatie van 0,0 vinden, dan weten we dat de genen geen invloed hebben gehad. Uit verzameld onderzoek naar mensen van verschillende leeftijden bleek de correlatie 0,75 te zijn. Dit betekent dat 75% van de variatie aan gewicht in de populatie toe te schrijven is aan genen.

Omdat MZ tweelingen die apart opgroeien erg zeldzaam zijn, komt het vaker voor dat MZ tweelingen vergeleken worden met tweeeiige tweelingen, ook wel dizygotische tweelingen (DZ) genoemd. DZ tweelingen hebben slechts 50% van hun genen met elkaar gemeen. Als genen geen invloed zouden hebben, dan zouden de MZ tweelingen evenveel van elkaar moeten verschillen als de DZ tweelingen. In de onderstaande afbeelding zien we de uitkomst van dit experiment, uitgevoerd bij 600 MZ en 600 DZ tweelingen van 16 jaar. Links vinden we een correlatie van 0,84 en rechts een correlatie van 0,55. Wederom zien we dus dat genen een rol spelen. Het verschil tussen de genetische overeenkomsten van MZ en DZ tweelingen (100 - 50 = 50%) komt overeen met het verschil tussen de twee correlaties (0,84 - 0,55 = 0,29). Als 50% van de genen dus een verschil maakt van 29%, dan maken alle genen een verschil van 29 × 2 = 58%. We vinden hier dus een correlatie van 0,58.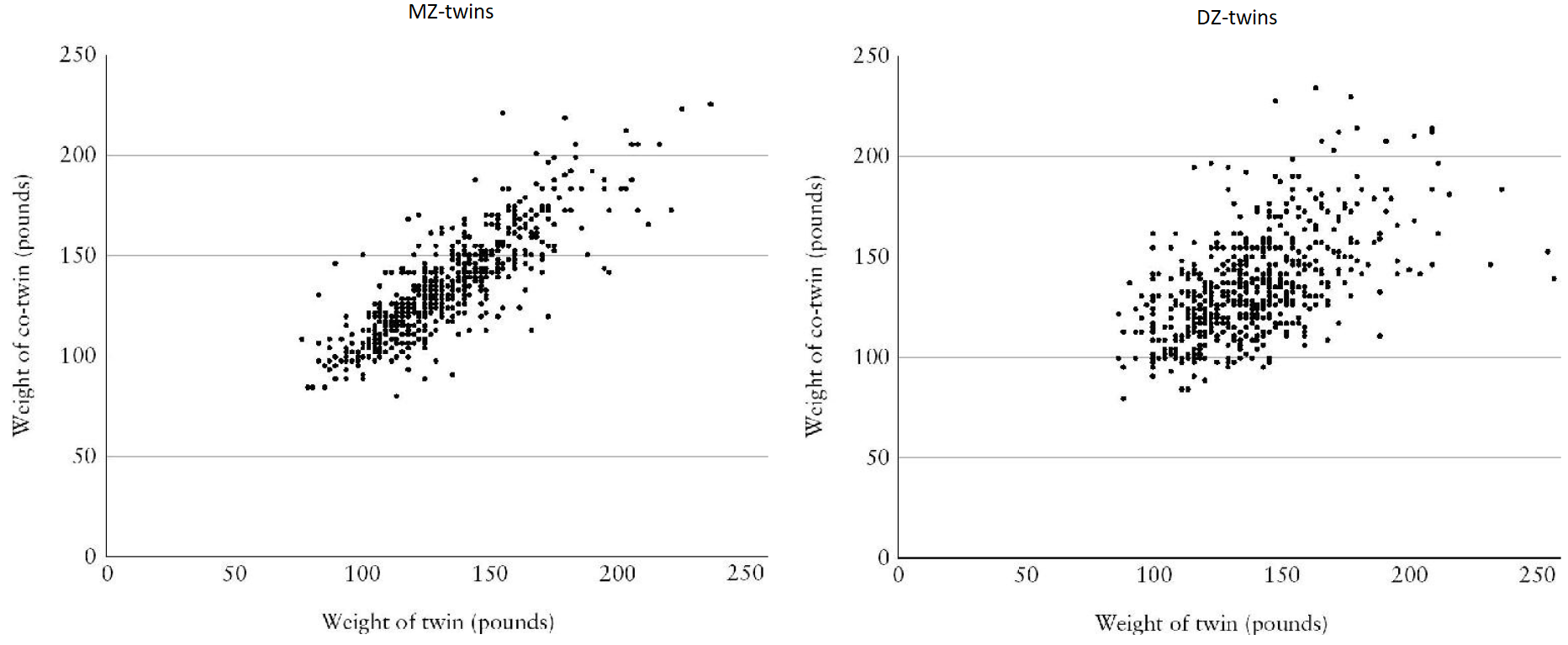

Bron: Blueprint, door Plomin (2019, Penguin Books)

Het verschil tussen de correlaties in beide onderzoeken (0,75 in de ene en 0,58 in de andere) bleek bij nader onderzoek te liggen aan het verschil in leeftijd. We weten nu dat bij jonge kinderen de correlatie 40% is, bij pubers is dus 60% en bij volwassenen wel 80%. Bij volwassenen is dus slechts 20% van de variatie in gewicht te verklaren door de omgeving. Dit verklaart waarom het voor mensen zo lastig is om hun gewicht aan te passen.

De echte shock kwam toen ouders werden vergeleken met zowel hun biologische als hun geadopdeerde kinderen. Het resultaat was een correlatie van 0,3 bij biologische kinderen. Omdat ouders en kinderen 50% genetisch overeenkomen, levert dit een correlatie van 0,3 × 2 = 0,6 voor de genen. Bij geadopteerde kinderen werd een correlatie van 0,0 gevonden! Het maakte dus geen verschil in welk gezin de kinderen opgevoed werden voor het gewicht dat ze uiteindelijk krijgen! We kunnen hieruit concluderen dat 60% van het gewicht genetisch te verklaren is, en dat de andere 40% niet door de opvoeding komt. Als je kinderen met overgewicht ziet en ze hebben ook ouders met overgewicht, dan is het dus onjuist te concluderen dat dit komt door de opvoeding van deze ouders. De enige causale relatie tussen het gewicht komt door de genen.

Hetzelfde resultaat vinden we als we biologische en geadopteerde kinderen met elkaar vergelijken. Biologische broers en zussen hebben een correlatie van 0,3, terwijl geadopteerde broers en zussen die in hetzelfde gezin opgroeien een correlatie hebben van 0,0. Ook werd ditzelfde resultaat verkregen als we biologische ouders vergelijken met biologische kinderen in hun eigen gezin en met biologische kinderen die geadopteerd zijn. We vinden hier in beide gevallen een relatie van 0,3 (het maakt dus geen verschil of de kinderen bij hun biologische ouders wonen of bij een willekeurig ander gezin).

Maar hoe is dit mogelijk? Blijkbaar kunnen ouders niet veel veranderen aan de eetlust van hun kind. Een kind zonder overgewicht bij ouders met overgewicht zal minder opscheppen of zijn bord niet leegeten. Een kind met overgewicht bij ouders zonder overgewicht zal zijn bord altijd leegeten, buitenshuis altijd vaak eten aannemen en als hij hongerig wordt zijn ouders lastig vallen tot zijn maagje vol zit.

Ik wilde nog wel even noemen dat dit niet betekent dat je niks aan overgewicht kan doen. Iedereen kent wel verhalen van mensen waarbij een dieet succesvol was, maar dit is zeldzaam genoeg dat dit niet zichtbaar wordt in deze data (gewichtverlies is ook vaak tijdelijk). Dit wil echter niet zeggen dat het onmogelijk dat deze situatie ooit zal verbeteren. Als er betere methodes komen om gedrag te veranderen, dan kan dat wel degelijk. We hebben een dergelijke verandering, maar in de verkeerde richting, bijvoorbeeld gezien in de afgelopen decennia. Omdat vettig eten tegenwoordig veel goedkoper is geworden, zijn mensen genetisch minder in staat dit eten te laten liggen en als gevolg spelen genen nu een grotere rol in het verklaren van overgewicht dan eerder het geval was.

Er komt nog één shocker achteraan. Het blijkt dat dezelfde redenering opgaat voor alle persoonlijkheidseigenschappen. Gemiddeld is 50% van deze eigenschappen bepaald door genen en zo goed als 0% door de opvoeding! Conclusie is dat het gedrag van onze ouders dus veel minder ons leven beinvloed dan vaak gedacht wordt (uitzonderingen zijn zware mishandeling of verwaarlozing, dit heeft wel degelijk een grote impact).

Maar als 50% genetisch is en 0% door de opvoeding, wat is dan de andere 50%. Hier hebben wetenschappers decennia zonder resultaat naar gezocht. Wetenschappers hebben o.a. gekeken of dit komt doordat ouders verschillende kinderen verschillend behandelen, waardoor twee kinderen in hetzelfde gezin niet precies dezelfde opvoeding krijgen. Ook is er gekeken of misschien de vriendengroep op school een grote invloed uitoefent. Al deze fenomenen blijken echter weinig effect te hebben, blijken vaak van tijdelijke aard te zijn en lijken nauwelijks door interventie verbeterd te kunnen worden (in ieder geval niet met de kennis die we nu hebben). De effecten die wel gemeten werden, bleken meestal achteraf toch genetisch te verklaren te zijn. Bijvoorbeeld, welke vrienden je opzoekt op school hangt natuurlijk ook weer af van je persoonlijkheid. Uiteindelijk hebben wetenschappers geconcludeerd dat de andere 50% willekeurige gebeurtenissen in het leven zijn.

Bron: Blueprint, door Plomin (2019, Penguin Books)

Afleiding: Gedeelde variantie

In het bovenstaande stuk zijn o.a. eeneiige tweelingen met elkaar vergeleken. Er werd onderzocht hoeveel procent van de variantie van bijboorbeeld de massa van de tweelingen door de genen wordt bepaald en hoeveel door de opvoeding en andere factoren. De massa's die we meten (x) zullen dus bestaan uit een waarde die te verklaren is door wat de tweelingen gemeen hebben (namelijk de genen) en een deel dat willekeurig is (de omgeving etc.). Als we voor het gemeenschappelijke deel de letter T gebruiken (voor "true") en voor de rest de e (voor "error"), dan geldt dus:
$$ x = T + e $$
Eerder hebben we gezien dat:
$$ var(x_1 + x_2) = var(x_1) + var(x_2) + 2cov(x_1,x_2) $$ $$ var(x_1 - x_2) = var(x_1) + var(x_2) - 2cov(x_1,x_2) $$
Als we dit invullen voor x = T + e en voor e = x - T, dan vinden we:
$$ var(x) = var(T + e) = var(T) + var(e) + 2cov(T,e) $$ $$ var(e) = var(x - T) = var(x) + var(T) - 2cov(x,T) $$
De laatste term in de eerste vergelijking is nul, omdat er natuurlijk geen correlatie is tussen de echte waarde T en de willekeurige component e. Als we de eerste vergelijking dan in de tweede vergelijking substitueren, dan vinden we:
$$ var(e) = var(T) + var(e) + var(T) - 2cov(x,T) $$ $$ 0 = 2var(T) - 2cov(x,T) $$ $$ var(T) = cov(x,T) $$
Omdat ook geldt dat:
$$ cov(x_1,x_2) = cov(x_1,T+e_2) = cov(x_1,T) + cov(x_1,e_2) $$
De laatste term is hier wederom nul, omdat x₁ natuurlijk niet gecorreleerd is met e₂. Hiermee kunnen we schrijven dat:
$$ var(T) = cov(x_1,x_2) $$
We kunnen hiermee de formule voor de covariantie schrijven als:
$$ r = \frac{var(T)}{var(x)} $$
De correlatie geeft nu dus de fractie van de variantie die gedeeld wordt door de tweelingen. Omdat de tweelingen alleen de genen delen, weten we dus dat dit percentage aangeeft hoeveel procent van de variantie in de bevolking het gevolg is van genetische verschillen! We kunnen hiermee dus het eeuwenoude dilemma over "nature" en "nurture" oplossen.

Afleiding: de covariantie

In deze paragraaf hebben we de covariantie gedefinieerd als:
$$ cov(x,y) = \frac{1}{N}\sum{(x_i-\mu_x)(y_i-\mu_y)} $$
In termen van de verwachtingswaarde, kunnen we dit schrijven als:
$$ cov(x,y) = E[ (x - E[x])(y - E[y]) ] $$
Als we de haakjes uitwerken, dan vinden we:
$$ cov(x,y) = E[ xy - xE[y] -yE[x] +E[x]E[y]] $$ $$ cov(x,y) = E[xy] - E[x]E[y] - E[y]E[x] + E[x]E[y] ] $$ $$ cov(x,y) = E[xy] - E[x]E[y] $$
En dit is precies de uitspraak die we eerder in dit hoofdstuk de covariantie hebben genoemd.

Factoranalyse

In sommige gevallen zijn onderzoekers op zoek naar correlaties tussen een grote groep variabelen, om erachter te komen welke van deze variabelen gerelateerd zijn en welke niet. We spreken in zo'n geval van een factoranalyse. Het doel van deze analyse is om de variabelen op te delen in factoren. Een factor is een groepje aan variabelen die onderling gerelateerd zijn, maar die onafhankelijk zijn van de andere factoren. Om dit beter te begrijpen bespreken we hieronder meteen een bekend voorbeeld.

Toepassing: De "Big Five" persoonlijkheidseigenschappen

In de vorige eeuw gingen wetenschappers de correlatie meten tussen allerlei persoonlijkheidseigenschappen. Er werd o.a. gevonden dat mensen die enthusiast zijn ook meer spraakzaam zijn, meer assertief, meer sociaal etc. Het bleek dat al deze eigenschappen sterk met elkaar gecorreleerd waren. Uiteindelijk werden al deze begrippen onder de noemen extraversie geplaatst. Extraversie is dus een overkoepelende factor. Er bleken nog vijf andere onafhankelijke factoren te zijn: openheid (openheid voor nieuwe ervaringen), neuroticisme (sterke ervaring van emoties), "agreeableness" (meegaand) en "conscientiousness" (geordend en gedisciplineerd). Alle woorden die te maken hebben met persoonlijkheid kunnen dus onderverdeeld worden in één van deze vijf factoren, genaamd de "big five personality traits". Anders dan veel van de persoonlijkheidstesten die er in omloop zijn, is deze onderverdeling op harde wetenschap gebaseerd.

Een zelfde poging werd gedaan met verschillende soorten intelligentie. Er wordt vaak gedacht dat iedereen wel zijn intellectuele talenten heeft. De ene persoon is goed in rekenen en de ander in taal en weer een ander is juist erg creatief etc. Het blijkt echter dat al deze intellectuele vaardigheden sterk met elkaar gecorreleerd zijn. Er is dus maar één factor als het gaat om intelligentie. Deze factor wordt g genoemd en een IQ-test is de beste manier op g te meten (hoewel de IQ-test dit niet perfect doet).

Het blijkt dus dat mensen die goed zijn in rekenen, over het algemeen ook goed zijn in taal. En mensen die slechts zijn in rekenen, zijn over het algemeen ook slecht in taal. Dit lijkt in de druisen tegen de dagelijkse observatie. Heel veel mensen kunnen herinneren dat ze voor het ene vak veel hogere cijfers hadden dan voor het andere vak. Probleem is dat in een klas leerlingen met elkaar vergeleken worden met ongeveer hetzelfde IQ. Een VWO-er die zegt goed te zijn in rekenen, maar slecht in taal, is waarschijnlijk beter in zowel rekenenen als taal dan de gemiddelde HAVO-er.

Het Pareto principe

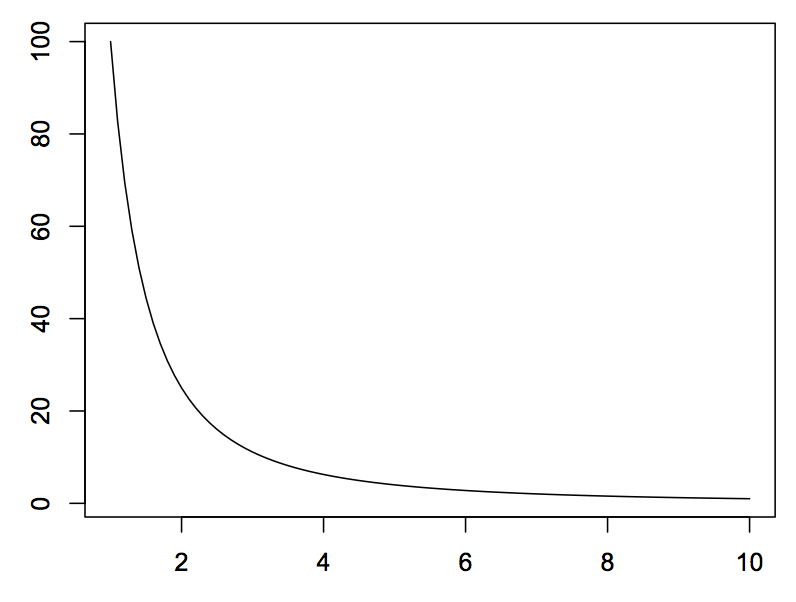
De normale verdeling komt vaak voor in de wetenschap, maar er zijn nog veel meer soorten verdelingen. Een van deze verdelingen is de zogenaamde Lotka verdeling. In de onderstaande afbeelding zien we een voorbeeld. Zoals je ziet begint de grafiek hoog en neemt daarna erg snel af. In deze verdeling zitten dus bijna alle punten bij de nul en slechts een paar uitschieters bij hogere waarden.

Dit fenomeen vinden we bijvoorbeeld ook bij het aantal publicaties van wetenschappers. 60% van de wetenschappers had slechts 1 artikel gepubliceerd gekregen. 15% had een tweede artikel op zijn naam staan en slechts 2,5% had meer dan 5 artikelen gepubliceerd. Slechts een klein groepje wetenschappers produceert dus bijna alle nieuwe kennis. Denk bijvoorbeeld aan Einstein, die de speciale relativiteitstheorie ontdekte en toen ook de algemene relativiteitstheorie (twee enorme vakgebieden binnen de natuurkunde), het bestaan van atomen aantoonde, de basis legde van de kwantummechanica en van de werking van lasers.

Een ander sterk voorbeeld is te vinden in de klassieke muziek. Slechts vier componisten (Bach, Beethoven, Mozart en Tchaikovsky) hebben bijna alle muziek geschreven die door moderne klassieke orkesten wordt gespeeld. Een ander voorbeeld zijn bestsellers. In boekwinkels over de hele wereld zie je vaak dezelfde werken liggen. De meeste schrijvers verkopen maar een paar boeken (en hebben dus vaak financiele problemen), terwijl een paar uitschieters miljoenen boeken verkoopt. Ook in sport zien we dit effect vaak. Bij tennis zie je bijvoorbeeld bij zo goed als elk tournooi al jaren dezelfde paar namen terug (Federer, Nadal en Djokovic). Deze tennissers winnen dus jaren op rij van zo goed als alle andere spelers, totdat ze elkaar in de halve finale en de finale weer tegenkomen. Op dit moment heeft Nadal bijvoorbeeld 100 van de 102 wedstrijden gewonnen op Roland Garros en hebben Nadal en Federer elk 20 grand slam titels op hun naam staan.

We kunnen zien wat hier aan de hand is in het onderstaande programma. In de bovenste afbeelding zien we een populatie sporters met een normaal verdeeld talent. Daaronder zien we een diagram met op de horizontale as het aantal wedstrijden dat een persoon gewonnen heeft en op de verticale as het aantal sporters dat dit aantal wedstrijden gewonnen heeft. Als een spel gemiddeld moeilijk is, dan zien we hier ook een normale verdeling verschijnen. Als we het spel echter moeilijker maken, dan vormt de normale verdeling zich om tot een lotka curve. In dit geval wint bijna niemand, behalve een paar uitschieters. Iets soortgelijks gebeurt als we het steeds gemakkelijker maken om te winnen. In dat geval wint bijna iedereen.

Toepassing: Golf

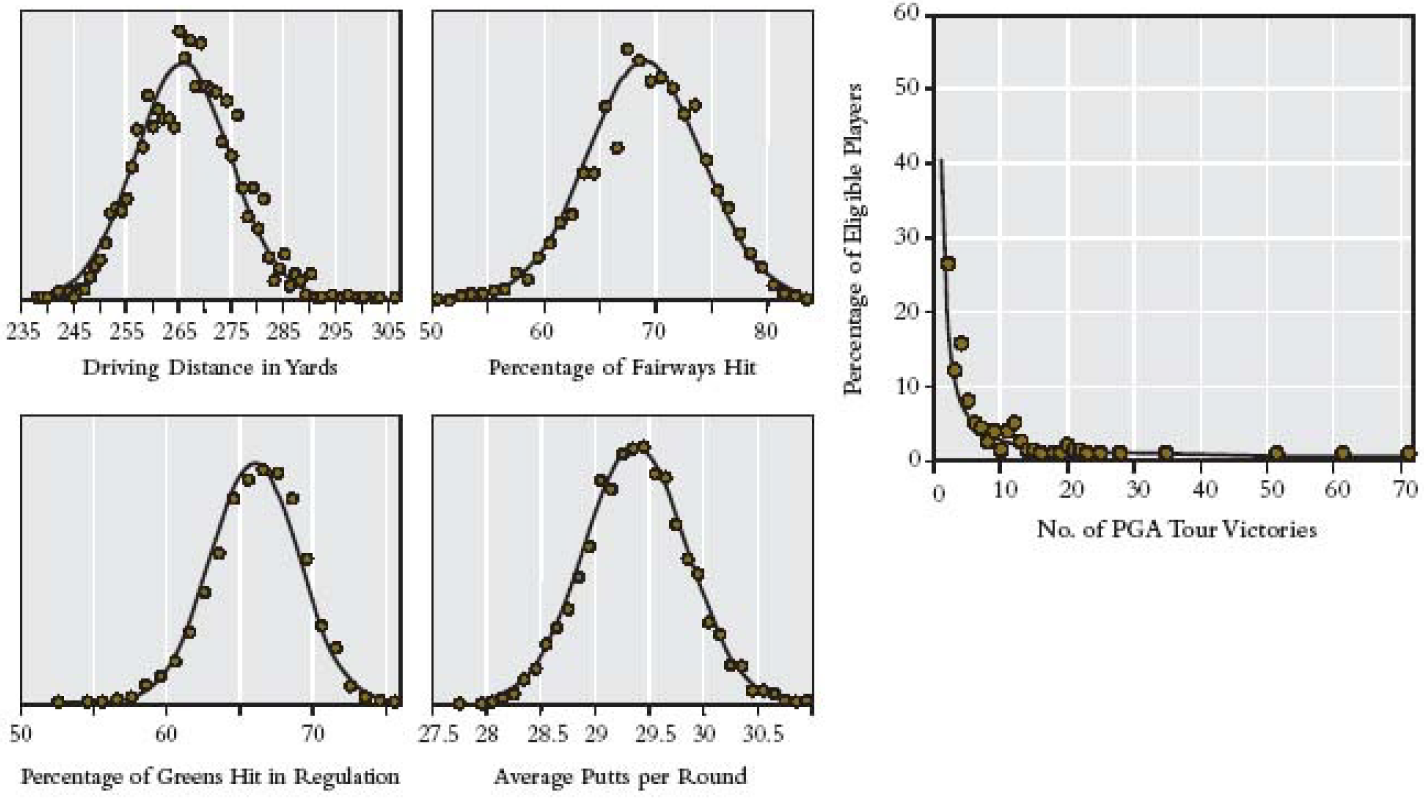
Dit effect is bijvoorbeeld goed te zien in de statistieken over professionele golfers. Links zien we de verdeling van vier individuele vaardigheden die belangrijk zijn bij golf. Zoals je ziet is de verdeling van al deze vaardigheden normaal verdeeld. Rechts zien we de verdeling van het aantal tournooiwinsten. We zien dat de meeste professionals nog nooit een tournooi gewonnen hebben. Slechts vier spelers hebben meer dan 30 tournooien gewonnen en slechts één speler heeft er meer dan 70 gewonnen. Alle winst gaat dus maar naar een paar individuen.

Bron: Human Accomplishment: The Pursuit of Excellence in the Arts and Sciences, door Murray (2003, HarperCollins)

Toepassing: Tinder

We kunnen dit effect ook zien in de dating wereld. Een kleine percentage mannen wekt interesse bij bijna alle vrouwen, terwijl de meeste mannen amper interesse wekken bij de meeste vrouwen. Dit is tegenwoordig gemakkelijk te meten met datingapps. Een paar mannen krijgt op deze apps heel veel "matches", terwijl de meerderheid er slechts een paar krijgt. Als gevolg heeft slechts een klein groepje mannen redelijke keuzevrijheid, hetgeen natuurlijk belangrijk is om een geschikte partner te vinden.

Hier zijn de statistieken. Het blijkt dat de 20% knapste mannen keuze hebben uit 78% van de vrouwen, terwijl de andere 80% van de mannen keuze heeft uit de 22% minst knappe vrouwen. De statistieken zijn zo scheef dat een man die gemiddeld aantrekkelijk is, slechts een match krijgt met 0,87% van de vrouwen (voor de mooiste mannen is dit boven de 10%). Gemiddeld gezien krijgen vrouwen 6,2 keer zoveel matches (dus voor elke 10 matches die een gemiddelde man krijgt, krijgt de gemiddelde vrouw er 62). Als we met de zogenaamde Gini coefficient de ongelijkheid meten die we hier vinden, dan blijkt deze groter te zijn dan in 95% van de nationale economiën in de wereld.

Vrouwen hebben dus alle keus en de grote meerderheid van de mannen niet. Het zal je niet verbazen dat dit voor veel frustatie zorgt bij veel mannen. Een aantal mannen lukt het om met een beter kapsel, stoere kleding en goede foto's toch hun kansen te vergroten (dit is sowieso een goede investering, mits men niet te obsessief met uiterlijk bezig is), maar dit is zeker niet de norm.

Extra stof Statistiek