Extra stof hoofdstuk beweging
Poolcoördinaten
§1 Introductie
In de komende hoofdstukken gaan fundamentele natuurwetten bestuderen. Dit doen we door beweging en kracht te bestuderen. We noemen dit vakgebied de mechanica.
De eerste succesvolle mechanica was de mechanica van Newton. Het lukte Newton met zijn mechanica om zowel de beweging van vallende voorwerpen op aarde als de beweging van hemellichamen precies te beschrijven.
Het begon allemaal met het volgende idee. Newton stelde zich voor dat een groot kanon op aarde een kogel zou afschieten, die precies een snelheid had zodat de kromming van de val van de kogel gelijk zou zijn aan de kromming van de aarde. In dat geval zou de kogel altijd blijven vallen, maar nooit de aarde bereiken.
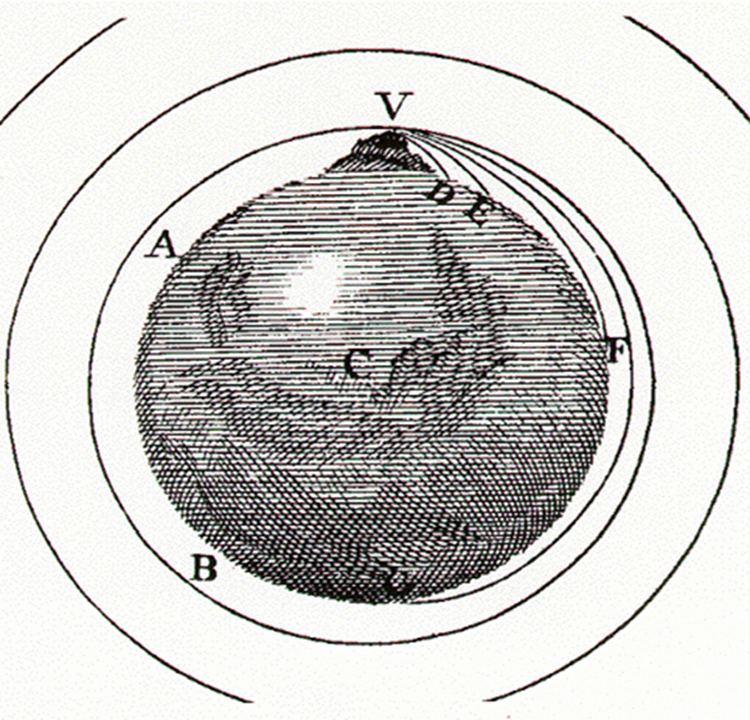
Op deze manier werd het mogelijk om de beweging van bijvoorbeeld de maan in zijn baan om de aarde te beschrijven met dezelfde zwaartekracht die er op aarde voor zorgt dat voorwerpen vallen.
In deze paragraaf gaan we uitrekenen hoe groot de valversnelling van de maan moet zijn om in zijn baan te blijven. Eerst is het echter nodig om iets te weten te komen over een wiskundige techniek genaamd differentiëren.
Differentiëren
Zoals je weet gebruiken we voor de positie van een voorwerp de letter x. Als we willen weten hoeveel de positie verandert gedurende een bepaalde tijdsduur Δt, dan gebruiken we de volgende formule:
$$ v = \frac{\Delta x}{\Delta t} $$In het hoofdstuk "beweging" hebben we gezien dat we ook de snelheid op één moment kunnen bepalen. Dit doen we met een raaklijn.
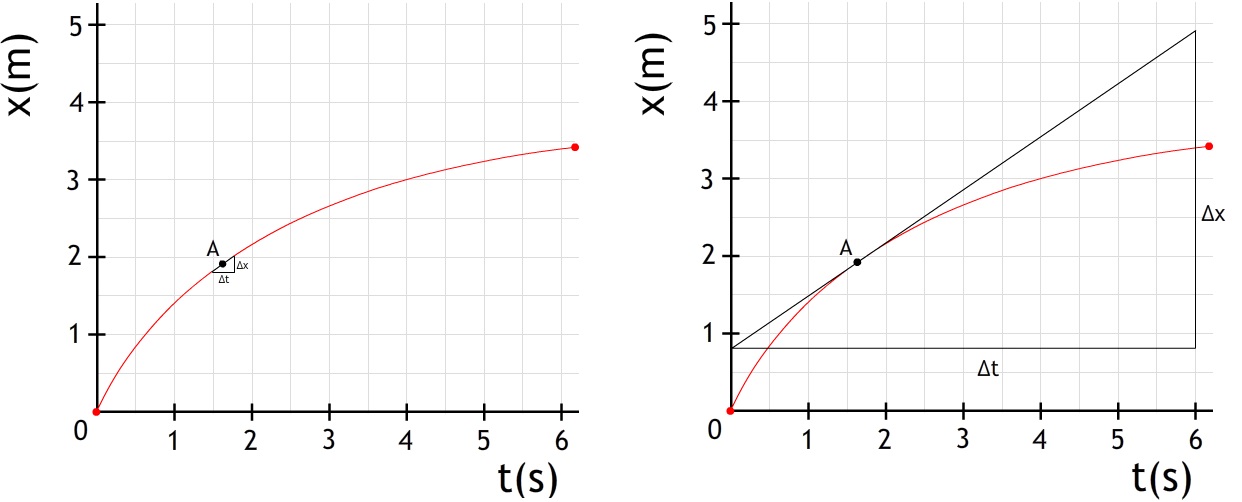
Met een raaklijn bepalen we de helling (richtingscoëfficient) gedurende een oneindig klein tijdstapje. In deze extra hoofdstukken zullen we de formule voor de snelheid op één moment weergeven als:
$$ v = \frac{dx}{dt} $$We noemen dit ook wel de de afgeleide van de positie naar de tijd.
Omdat we "d/dt" heel vaak gaan tegenkomen, gaan we dit vaak korter opschrijven als:
$$ v = \frac{dx}{dt} \equiv \dot{x} $$Hoeveel de snelheid verandert in de tijd noemen we de versnelling. De versnelling is dus de afgeleide van de snelheid naar de tijd. In de nieuwe notatie schrijven we:
$$ a = \frac{dv}{dt} \equiv \ddot{x} $$Soms gaan we ook de afgeleide nodig hebben van een vermenigvuldiging van twee variabelen. Neem bijvoorbeeld twee willekeurige variabelen x en y:
$$ \frac{d(xy)}{dt}$$De noemer kunnen we uitschrijven tot:
$$ d(xy) = x_ey_e - x_by_b $$In wat volgt gaan we aantonen dat we dit ook kunnen herschrijven tot:
$$ d(xy) = dx \cdot y_{gem} + dy \cdot x_{gem} $$Je kan nagaan dat dit klopt door de rechterzijde uit te werken:
$$ d(xy) = (x_e - x_b) \left( \frac{y_b+y_e}{2} \right) + (y_e - y_b)\left( \frac{x_b+x_e}{2} \right) $$Als we dit buiten haakjes plaatsen, dan vinden we:
$$ d(xy) = \frac{1}{2}x_ey_b + \frac{1}{2}x_ey_e - \frac{1}{2}x_by_b - \frac{1}{2}x_by_e + \frac{1}{2}y_ex_b + \frac{1}{2}y_ex_y - \frac{1}{2}y_bx_b - \frac{1}{2}y_bx_e $$Dit kunnen we vereenvoudigen tot:
$$ d(xy) = x_ey_e - x_by_b $$Dit is gelijk aan de uitspraak waar we mee begonnen. Er geldt dus inderdaad dat:
$$ d(xy) = dx \cdot y_{gem} + dy \cdot x_{gem} $$Als we beide kanten door dt delen, dan vinden we:
$$ \frac{d(xy)}{dt} = \dot{x}y_{gem} + \dot{y}x_{gem} $$Omdat we bij een afgeleide naar een verplaatsing kijken tijdens een oneindig klein tijdstapje, ligt xb, xe en xgem allemaal zo goed als op hetzelfde punt. Al deze punten zouden we dus ook gewoon x kunnen noemen (en hetzelfde geldt voor y). We vinden hiermee:
$$ \frac{d(xy)}{dt} = \dot{x}y + \dot{y}x $$We noemen dit de productregel.
In deze paragraaf gaan we ook de afgeleide nodig hebben van de sinus en de cosinus van een variabele. Zonder dit af te leiden, geef ik hier het resultaat:
$$ \frac{d \cos(\theta)}{dt} = -\dot{\theta}\sin(\theta) $$ $$ \frac{d \sin(\theta)}{dt} = \dot{\theta}\cos(\theta) $$Beweging in poolcoördinaten
Nu we de benodigde wiskunde gehad hebben, gaan een methode aanleren waarmee we cirkelbewegingen kunnen beschrijven. Dit gaan we daarna gebruiken om de beweging van de maan om de aarde te beschrijven.
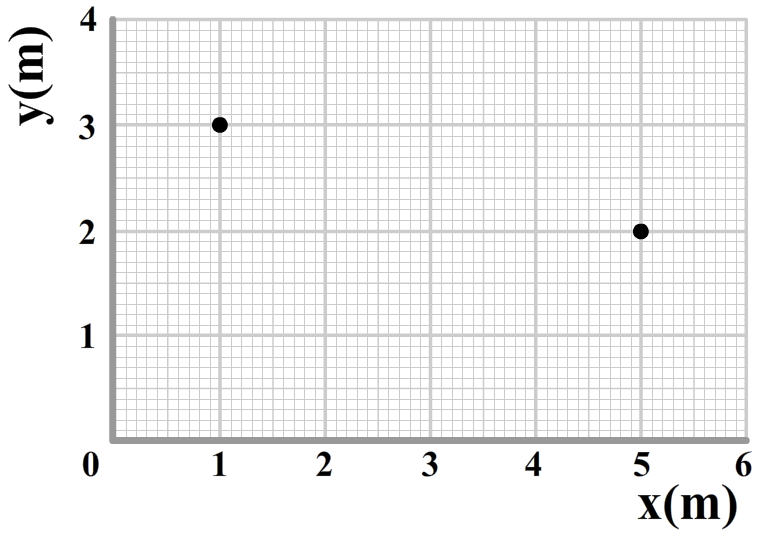
We moeten het hiervoor eerst over coördinaten hebben. Meestal geven we de locatie van een punt in een diagram door de x- en de y-coördinaat te noemen. We noemen dit cartesische coördinaten. Er zijn echter andere manieren om dit te doen. Een bekend alternatief zijn de poolcoördinaten. Hier wordt een punt in een diagram niet aangegeven met een x en een y, maar met de afstand vanaf de oorsprong (r) en de hoek met de x-as (θ). We zien dit in de onderstaande afbeelding weergegeven. Deze tweede methode blijkt veel prettiger werken bij het beschrijven van cirkelbewegingen.
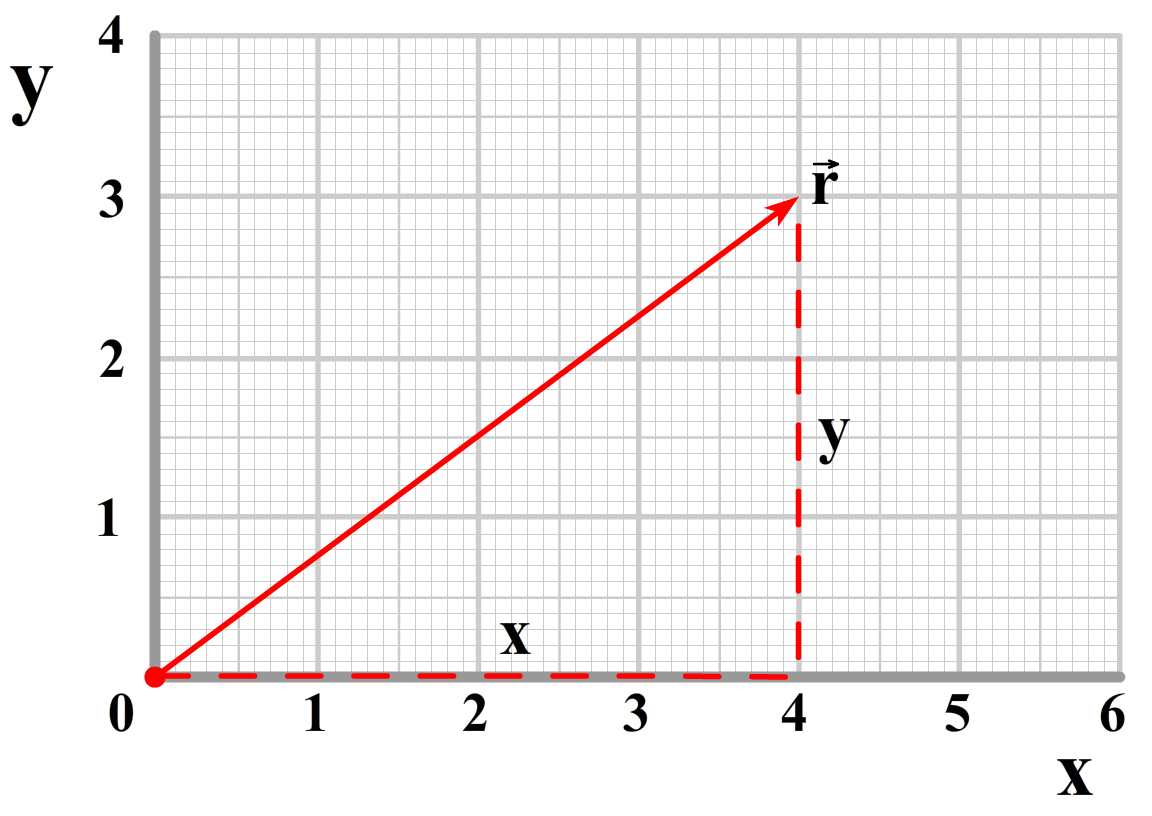
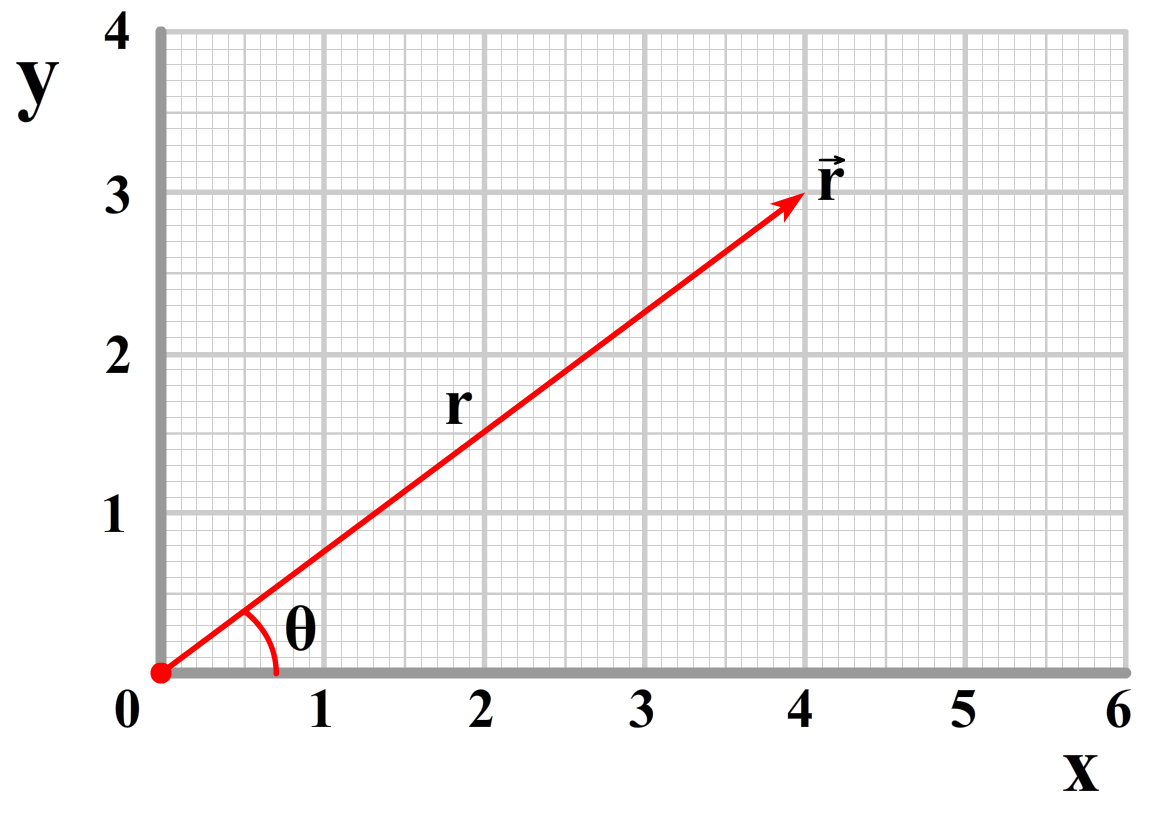
We kunnen de x- en de y-coördinaat ook schrijven in termen van r en θ. Dit doen we met de sinus en de cosinus, zoals in de onderstaande afbeelding is weergegeven. We vinden:
$$x = r\cos(\theta)$$ $$y = r\sin(\theta)$$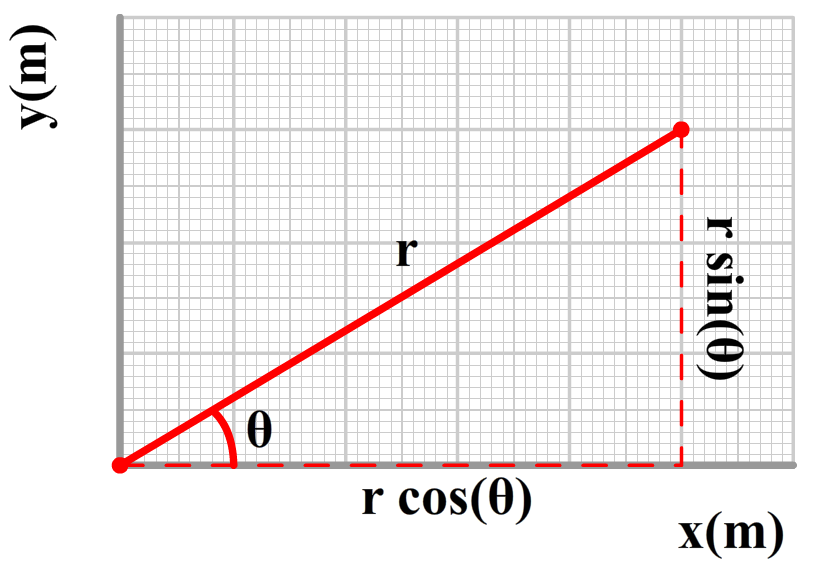
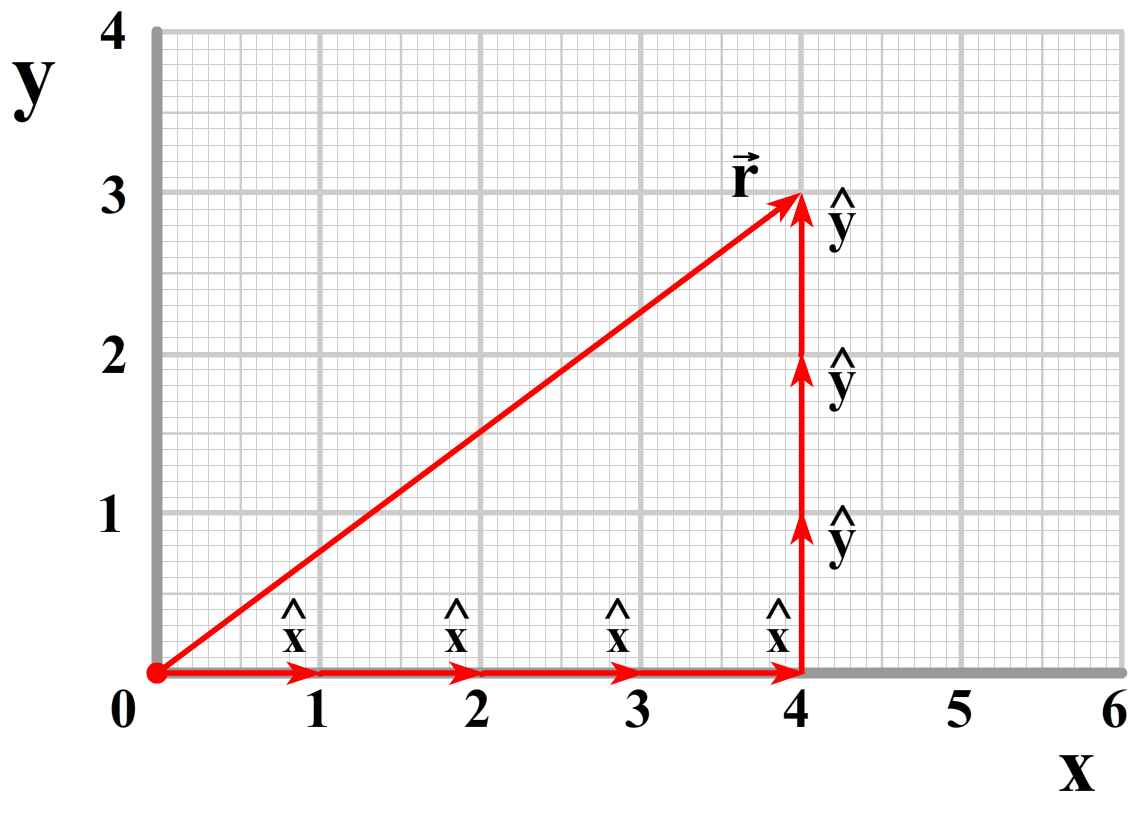
De positie wordt in de bovenstaande gevallen beschreven met een zogenaamde radiusvector (\(\vec{r})\). Dit is een vector die wijst van de oorsprong naar een bepaalde coördinaat (vectoren geven we weer met een pijltje boven de letter). In cartesische coordinaten kunnen we deze pijl beschrijven als:
$$ \vec{r} = x\hat{x} + y\hat{y}$$De x staat hier voor de lengte van de radiusvector in de x-richting. De y voor de lengte van de radiusvector in de y-richting. In het bovenstaande voorbeeld geldt bijvoorbeeld x = 4 en y = 3. De x en de y met een dakje noemen we eenheidsvectoren. Dit zijn vectoren met lengte 1 die resp. in de x- en y-richting wijzen.
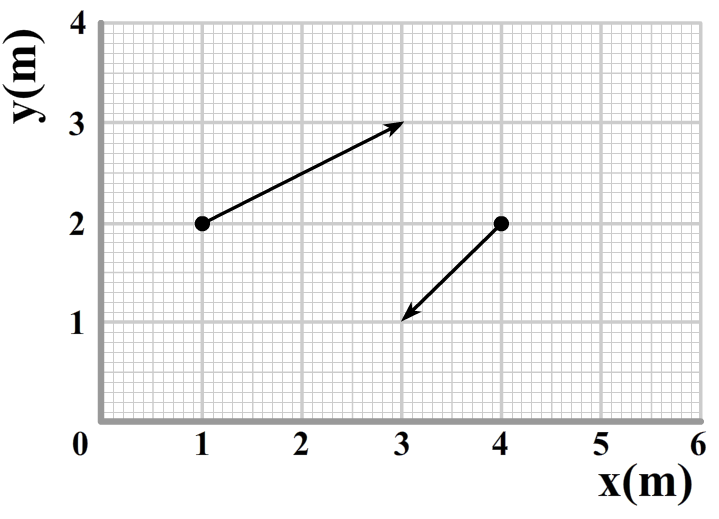
Nu we de positie hebben beschreven in beide coördinatenstelsels, zijn we klaar voor de snelheid. Stel ons punt beweegt van punt A naar punt B tijdens een bepaalde tijdseenheid (zie de onderstaande afbeelding).
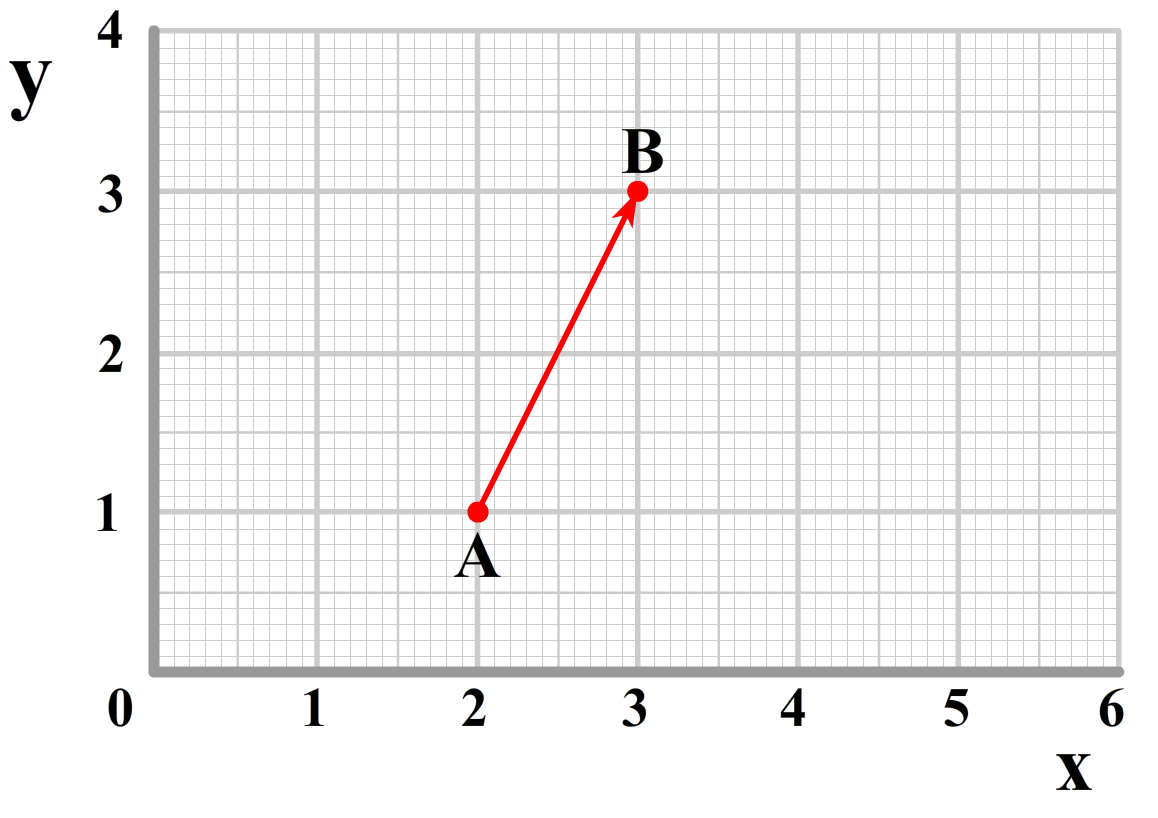
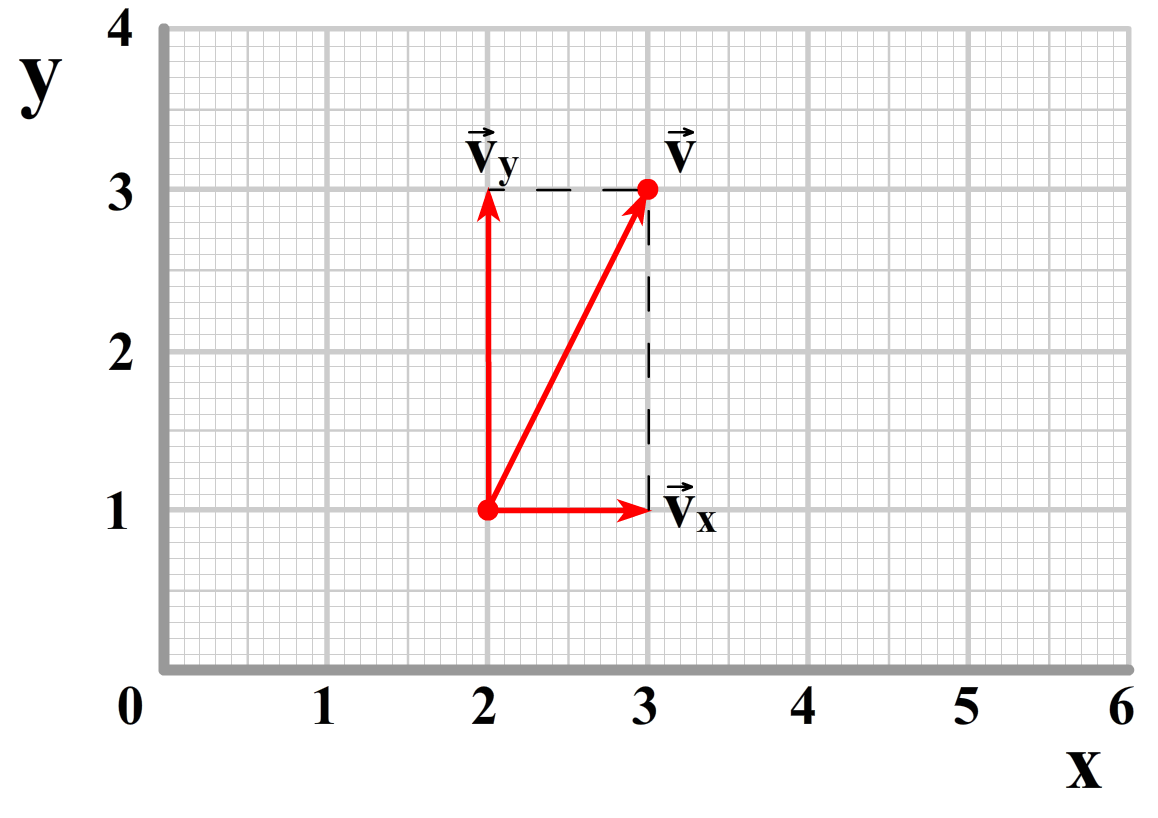
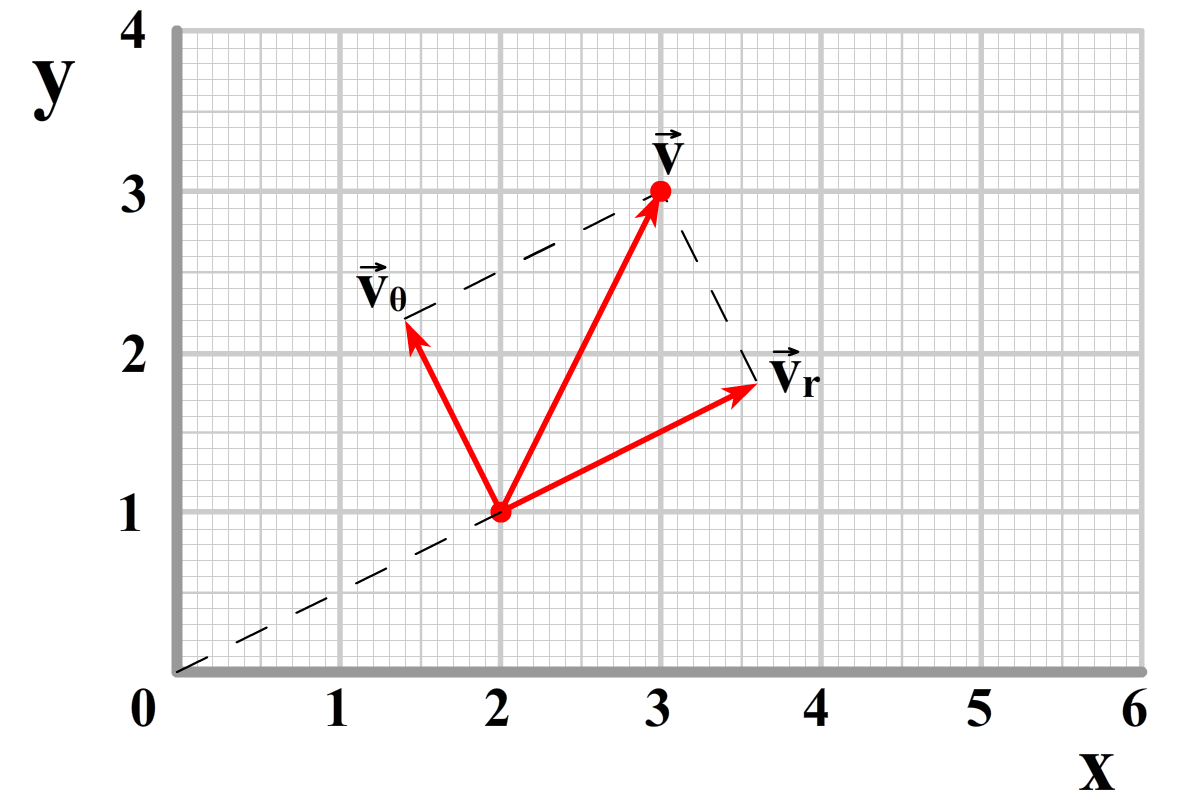
Ook deze beweging kunnen we weer op twee manieren beschrijven. In de onderstaande linker afbeelding zien we de snelheid opgedeeld in een x- en een y-component. In de rechter afbeelding is de snelheid opgedeeld in een r- en een θ-component. We kunnen de snelheid dus op de volgende twee manieren schrijven:
$$ \vec{v} = v_x\hat{x} + v_y\hat{y} $$ $$ \vec{v} = v_r\hat{r} + v_\theta\hat{\theta} $$De eenheidsvector van r wijst weg van de oorsprong en de eenheidsvector van θ staat hier loodrecht op (in de draairichting bij het groter maken van de hoek).
Met behulp x = rcos(θ) en y = rsin(θ) kunnen we vx en vy schrijven als:
$$ v_x = \frac{dx}{dt} = \frac{d(r\cos{\theta})}{dt} = \dot{r}\cos{\theta} - r\dot{\theta}\sin{\theta}$$ $$ v_y = \frac{dy}{dt} = \frac{d(r\sin{\theta})}{dt} = \dot{r}\sin{\theta} + r\dot{\theta}\cos{\theta}$$De snelheidsvector wordt hiermee:
$$ \vec{v} = (\dot{r}\cos{\theta} - r\dot{\theta}\sin{\theta})\hat{x} + (\dot{r}\sin{\theta} + r\dot{\theta}\cos{\theta})\hat{y} $$Dit kunnen we herschrijven tot:
$$ \vec{v} = \dot{r} (\cos{\theta}\;\hat{x} + \sin{\theta}\;\hat{y} ) + r\dot{\theta}(- sin{\theta}\;\hat{x} + \cos{\theta}\;\hat{y})$$Deze formule kunnen we gelukkig enorm versimpelen. In de onderstaande afbeelding kunnen we zien dat we met behulp van de sinus en de cosinus deze eenheidsvectoren ook kunnen schrijven als:
$$ \hat{r} = cos{\theta}\;\hat{x} + sin{\theta}\;\hat{y} $$ $$ \hat{\theta} = -sin{\theta}\;\hat{x} + cos{\theta}\;\hat{y} $$We hebben hier gebruikt dat de lengte van de eenheidsvectoren gelijk is aan 1. Het minnetje in de tweede regel komt omdat deze component naar links wijst.
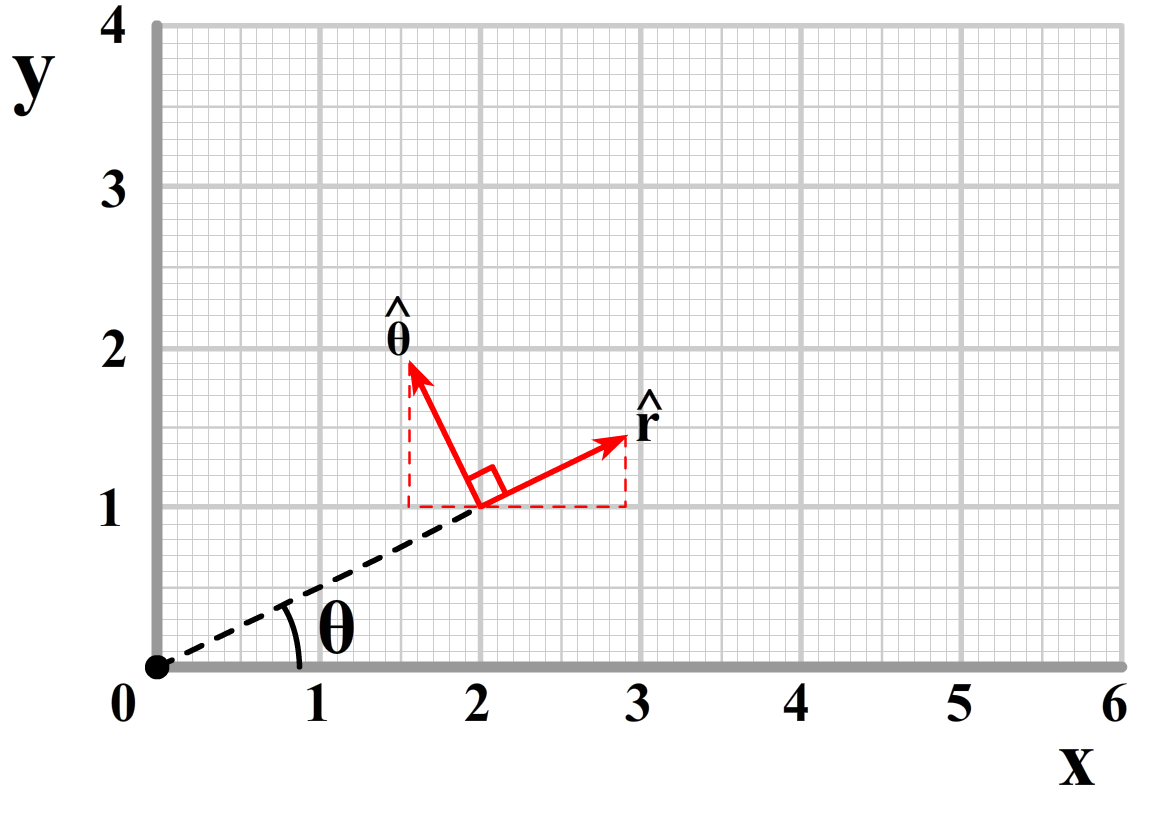
Met deze resultaten kunnen we de formule voor de snelheidsvector als volgt versimpelen:
$$ \vec{v} = \dot{r}\hat{r} + r\dot{\theta} \hat{\theta} $$Er geldt dus:
$$ v_r = \dot{r} $$ $$ v_\theta = r\dot{\theta} $$Op gelijke wijze kunnen we ook de versnelling in poolcoördinaten vinden. Als je dit uitwerkt vindt je:
$$ \vec{a} = (\ddot{r} - r\dot{\theta}^2) \hat{r} + (2\dot{r}\dot{\theta} + r\ddot{\theta}) \hat{\theta} $$Er geldt hier dus:
$$ a_r = \ddot{r} - r\dot{\theta}^2 $$ $$ a_\theta = 2\dot{r}\dot{\theta} + r\ddot{\theta} $$De eerste formule kunnen we ook nog herschrijven met \(v_\theta = r\dot{\theta}\). We vinden dan:
$$ a_r = \ddot{r} - \frac{v_\theta^2}{r} $$Deze resultaten gaan we hieronder gebruiken.
De maan om de aarde
We zijn nu eindelijk in staat de beweging van de maan om de aarde te bestuderen. In eerste instantie nemen we aan dat de maan een cirkelbaan om de aarde maakt en met een constante snelheid beweegt (dit is bij benadering waar). In dat geval wordt de versnelling van de maan in poolcoördinaten meteen een stuk simpeler. Voor de versnelling in de θ-richting vinden we:
$$ a_\theta = 2\dot{r}\dot{\theta} + r\ddot{\theta} = 0 $$De linker term is nul omdat de straal bij een cirkelbaan constant is. De veranderingen van de straal is dus nul. De tweede term vinden we de dubbele afgeleide van de hoek. Dit is de hoekversnelling. Omdat de maan met een constante snelheid voortbeweegt is dit gelijk aan nul.
Voor de versnelling in de radiusvector vinden we:
$$ a_r = \ddot{r} - \frac{v_\theta^2}{r} = -\frac{v_\theta^2}{r} $$De eerste term is nul omdat de straal constant is. We houden over dat:
$$ a_r = -\frac{v_\theta^2}{r} $$Dit is de versnelling die nodig is om de maan in zijn baan om de aarde te houden. Newton had al een waarde voor zowel de baanstraal van de maan (3,85 × 108 m) en ook voor de omlooptijd (27,32 dagen = 2,36 × 106 s). Hiermee kan hij de baansnelheid berekenen:
$$ v_\theta = \frac{2\pi r}{T} = \frac{2\pi \times 3,85\times 10^8}{2,36\times 10^6} = 1,03 \times 10^3 \text{ m/s} $$Hiermee kunnen we de radiële versnelling bepalen:
$$ a_r = -\frac{v_\theta^2}{r} = -\frac{(1,03 \times 10^3)^2}{3,85\times 10^8} = -0,00273 \text{ m/s}^2 $$Dit is de valversnelling die de maan ervaart. Vanwege de grote afstand van de aarde is dit een stuk kleiner dan de 9,81 m/s2 die we op aarde gewend zijn. De valversnelling is over deze afstand dus een factor 9,81/0,00273 ≈ 3600 afgenomen.
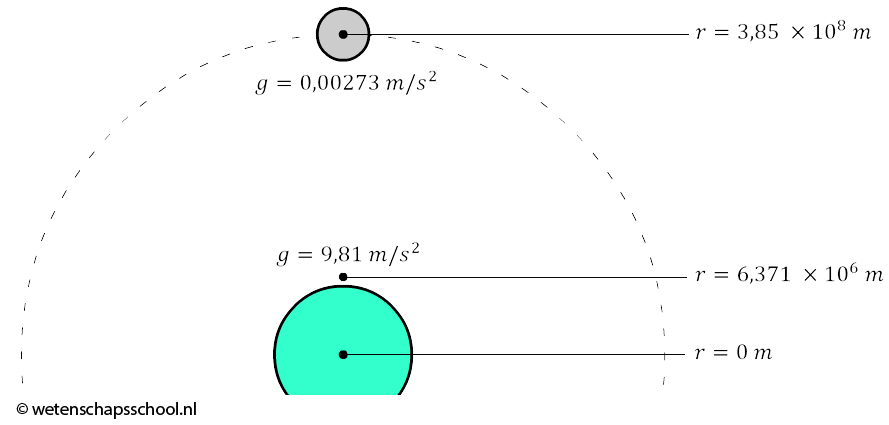
Newton wist ook dat de afstand van de aarde tot de maan 60× zo groot was als de straal van de aarde. Over deze afstand was de valversnelling 602 = 3600× afgenomen. We hebben hier dus te maken met een omgekeerd kwadratisch verband (als de afstand een bepaalde factor groter wordt, dan wordt g dezelfde factor in het kwadraat kleiner). Er geldt dus:
$$ g = \frac{\text{constante}}{r^2} $$Dit is Newton's beroemde "inverse squared law". In latere hoofdstukken gaan we laten zien dat we hiermee de beweging van hemellichamen met extreme precisie kunnen beschrijven.
 Rekenen met positie, snelheid en versnelling in poolcoördinaten
Rekenen met positie, snelheid en versnelling in poolcoördinaten
|
|