Extra stof hoofdstuk trillingen
Fouriertransformatie
In deze paragraaf bestuderen we de oplossingen van de golfvergelijkingen voor een touw dat aan twee kanten vast zit. Een bekend voorbeeld hiervan is bijvoorbeeld de gitaarsnaar. Als we het touw op x = 0 en x = L vastmaken, dan geldt voor u(x,t) dat:
$$ u(0,t) = 0 $$ $$ u(L,t) = 0 $$In deze situatie blijkt de meest algemene oplossing van de golfvergelijking gelijk te zijn aan:
$$ u_n(x,t) = \sum_{n=1}^{\infty}\left( b_n \cos{\left( \frac{n\pi}{L} c t \right)} + B_n \sin{\left( \frac{n\pi}{L} c t \right)} \right) \sin{\left( \frac{n\pi}{L} x \right)} $$ $$ c \equiv \sqrt{\frac{F_s}{\rho}} $$In de opdrachten ga je laten zien dat dit inderdaad een oplossing is van de golfvergelijking.
We kunnen deze oplossing iets simpeler schrijven als we aannemen dat onze snaar op tijdstip t = 0 stil staat. In dat geval (zo zullen we later zien) wordt Bn gelijk aan nul. De vergelijking versimpelt in dat geval tot:
De formule wordt ook simpeler als we eerst naar de functie kijken op tijdstip t = 0. In dat geval kunnen we gebruiken dat sin(0) = 0 en cos(0) = 1. De vergelijking wordt dan gelijk aan:
$$ u_n(x,0) = \sum_{n=1}^{\infty} b_n \sin{\left( \frac{n\pi}{L} x \right)}$$Dit kunnen we uitschrijven als:
$$ u_n(x,0) = b_1 \sin{\left( \frac{\pi}{L} x \right)} + b_2 \sin{\left( \frac{2\pi}{L} x \right)} + b_3 \sin{\left( \frac{3\pi}{L} x \right)} + ... $$Stel dat de b1 = 1 kiezen en alle andere b's nul maken, dan vinden we de onderste golf in de onderstaande afbeelding. Als we b2 = 1 kiezen en de rest op nul zetten, dan vinden we de tweede golf van onder.
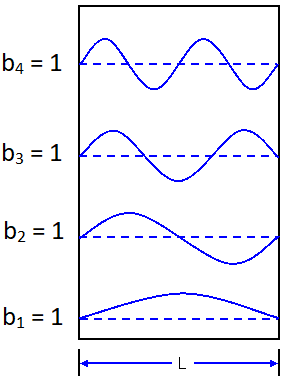
Maar wat nu als we de onderstaande golven willen maken? Met je vingers kan je een snaar in deze positie krijgen. Ook dit zijn dus oplossingen en moeten dus te maken zijn met de bovenstaande formule. We moeten in dat geval de waarden van bn slim kiezen, zodat de verschillende sinussen precies dit resultaat leveren. We gaan dit doen met behulp van de zogenaamde Fourieranalyse.
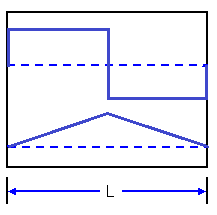
Om de waarden van bn te vinden, vermenigvuldigen we u(x,0) met sin(nπ/L x) en daarna integeren we van 0 tot L. Zometeen zal duidelijk worden waarom we dit doen.
$$ \int_{0}^{L} u(x,0)\sin{ (\frac{n\pi}{L} x)} dx = \int_{0}^{L} \left[ \sum_{n=1}^{\infty} b_n \sin{ \left( \frac{n\pi}{L} x \right)} \right] \sin{(\frac{n\pi}{L} x)} dx $$Met het programma Mathematica kan je deze integraal uitrekenen. We vinden:
$$ \int_{0}^{L} u(x,0)\sin{\left( \frac{n\pi}{L} x \right)} dx = b_n\frac{L}{2} $$Als we dit omschrijven, dan vinden we een formule waarmee we bn kunnen uitrekenen. Er geldt:
 Voorbeeld
Voorbeeld
|
|
Laten we de formule eens toepassen voor een snaar die op tijdstip t = 0 overal een uitwijking heeft van 1. De formule voor bn wordt dan: $$ b_n = \frac{2}{L} \int_{0}^{L} \sin{\left( \frac{n\pi}{L} x \right)} dx $$Als we deze formule in Mathematica stoppen (schrijf: "integrate 2/L*sin(n*pi/L*x) dx from 0 to L"), dan vinden we de volgende oplossing: $$ b_n = \frac{2-2\cos{(\pi n)}}{\pi n} $$Nu we de formule voor bn hebben, kunnen we deze formule terugstoppen in: $$ u_n(x,t) = \sum_{n=1}^{\infty} b_n \cos{\left( \frac{n\pi}{L} c t \right)} \sin{\left( \frac{n\pi}{L} x \right)} $$In het onderstaande programma hebben we deze formule ingevuld. We hebben gekozen voor c = 1 en L = 10. Je kan de "x", de "t" en de "n" in de formule laten staan in het programma. Het programma gebruikt "n" voor de sommatie. Onder de grafiek kan je instellen van tot welke waarde je de sommatie wil laten lopen. Let op als je te grote getallen neemt, dan het programma dan erg traag kan gaan lopen.
|
 Extra
Extra
|
|
De afgeleide van u(x,0) naar de tijd geeft de verticale snelheid van de snaar. De afgeleide van u naar t levert: $$ \dot{u}(x,t) = \sum_{n=1}^{\infty}{ \left[ -b_n c \frac{n\pi}{L} \sin{\left( c \frac{n\pi}{L} t \right)} + B_n c \frac{n\pi}{L} \cos{\left( c \frac{n\pi}{L} t \right)} \right] \sin{\left( \frac{n\pi}{L} x \right)} } $$Op tijdstip t = 0, wordt dit: $$ \dot{u}(x,0) = \sum_{n=1}^{\infty} B_n c \frac{n\pi}{L} \sin{\left( \frac{n\pi}{L} x \right)} $$Als we de term voor de sinus beschouwen als een constante, dan kunnen we weer de fourieranalyse toepassen om de waarde van deze constante te vinden: $$ B_n c \frac{n\pi}{L} = \frac{2}{L} \int_{0}^{L} \dot{u}(x,0) \sin{ \left(\frac{n\pi}{L} x \right) } dx $$Nu schrijven we de formule om, zodat we er Bn mee kunnen uitrekenen:
$$ B_n = \frac{2}{ c n\pi} \int_{0}^{L} \dot{u}(x,0) \sin{ \left( n\pi x \right)} dx $$
Let erop dat Bn automatisch nul wordt als de snaar stilstaat op t = 0. In dat de geval is \( \dot{u} \) op tijdstip t = 0 namelijk nul.
|
 Construeren van golven met fouriertransformatie
Construeren van golven met fouriertransformatie
|
|
In de vorige paragraaf hebben we gezien dat we een functie f(x) van x = 0 tot x = L altijd kunnen schrijven als:
$$ f(x) = \sum_{n=1}^{\infty} b_n \sin{ \left( \omega x \right)} $$ $$ b_n = \frac{2}{L} \int_{0}^{L} f(x) \sin{\left( \omega x \right)} dx $$We kunnen deze techniek ook toepassen op een geluidstrilling u(t). Stel dat we een geluidsgolf binnenkrijgen in een microfoon, dan kunnen we met behulp van een oscilloscoop een (u,t)-diagram maken. Van de grafiek in dit diagram kunnen we dan een fourierreeks uitschrijven tot:
De betekenis van ω in deze formule kunnen we achterhalen door deze formule te vergelijken met de formule voor de harmonische trilling:
$$ u(t) = A \sin{ \left( \frac{2\pi t}{T} \right) } = A \sin{(2\pi f t)} $$We vinden:
$$ \omega = 2\pi f $$In dit geval is de ω dus gerelateerd aan de frequentie van de trilling.
Nu de interpretatie van de constantes bn. Hier geldt:
$$ b_n = A $$De formule vertelt ons dus dat we elke trilling u(t) te schrijven is als een combinatie van sinussen met frequentie f en amplitude A. Elke trilling is dus te maken door slim sinussen bij elkaar op te tellen. Anders gezegd, we kunnen op deze manier dus achterhalen welke tonen er verstopt zitten in een trilling die de microfoon oppikt. Dit kunnen we goed weergeven als we bn uitzetten tegen de frequentie. We spreken hier van een geluidsspectrum. Onder aan de onderstaande afbeelding zien we hier een voorbeeld van:
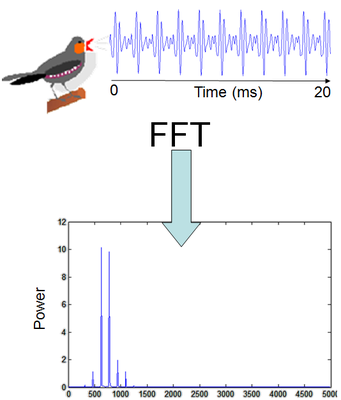
Hieronder zien we nog een voorbeeld. Boven zien we het (u,t)-diagram van een geluid van een bepaalde vogel. Onder zien we de verschillende frequenties die in het signaal verstopt zitten.
Hieronder is dit gedaan met het geluidssignaal dat de microfoon van de computer ontvangt:
Deze techniek heeft wordt veel toegepast in het dagelijks leven. Stel dat we bijvoorbeeld de bastonen uit een signaal willen halen, dan voeren de eerst een fouriertransformatie op het signaal uit. We halen dan de lage frequenties uit het signaal en daarna zetten we het signaal terug naar een geluidssignaal die via de luidsprekers weer kan worden uitgezonden.
Omdat bn dus afhankelijk is van de frequentie, schrijven wordt de constante ook wel gezien als een functie afhankelijk van ω: \(\hat{u}(\omega)\). In deze vorm spreken we van de fouriertransformaties:
Zoals je ziet geven deze formules een manier om een trilling (u(t)) om te schrijven naar een spectrum (\(\hat{u}(\omega)\)) en andersom.
We kunnen de fouriertransformatie ook uitbreiden, zodat deze geldig is van x is min oneindig tot oneindig. In dat geval verandert de som in een integraal en verandert de sinus in een factor eiωt. De afleiding hiervan wordt hieronder gegeven. Het resultaat is:
Dit is de meest gebruikte vorm van de fouriertransformaties.
We gaan nu een meer algemene vorm van de fourierreeks afleiden. Stel je een willekeurige stuksgewijs-continue en periodieke functie f(x) voor met een periode van 2L. Met fourieranalyse kan dan worden laten zien dat we f(x) altijd kunnen schrijven als een reeks van sinussen en cosinussen:
We gaan nu formules afleiden om de constanten a0, an en bn te vinden, zodat we de gewenste functie f(x) terugkrijgen.
Om de formule voor a0 te vinden, beginnen we met het integreren van f(x) van -L naar L:
$$ \int_{-L}^L f(x) dx = \int_{-L}^L \left[ a_0 + \sum_{n=1}^{\infty}{(a_n \cos{(\omega x)} + b_n \sin{(\omega x)})} \right] dx $$Onder aan de paragraaf vinden we een programma waarmee we kunnen integreren. Als we deze formule hierin stoppen, dan vinden we:
$$ \int_{-L}^L f(x) dx = 2L a_0 $$Als we nu beide kanten delen door 2L, dan vinden we onze formule voor a0:
an vinden we door f(x) te vermenigvuldigen met cos(ω x) en dan integreren:
$$ \int_{-L}^L f(x) \cos{\left(\omega x \right)} dx = \int_{-L}^L \left[ a_0 + \sum_{n=1}^{\infty}{(a_n \cos{\left( \omega x \right)} + b_n \sin{\left( \omega x \right)})} \right] \cos{\left(\omega x \right)} dx $$Als we deze integraal uitwerken, dan vinden we:
$$ \int_{-L}^L f(x) \cos{\left( \omega x \right)} dx = La_n $$Als we delen beide kanten delen door L, dan vinden we de formule voor bn:
De formule voor bn vinden we op dezelfde wijze:
Stel dat we een geluidsgolf binnenkrijgen in een microfoon, dan kunnen we met behulp van een oscilloscoop een (u,t)-diagram maken. De grafiek in dit diagram kunnen we een fourierreeks van maken. Er geldt dan:
$$ u(t) = a_0 + \sum_{n=1}^{\infty}{ \left(a_n \cos{ \left( \omega t \right)} + b_n \sin{ \left( \omega t \right)} \right)} $$We kunnen de fourierreeks drastisch versimpelen, met behulp van de volgende wiskundige gelijkheden:
$$ e^{it} = \cos{t} + i \sin{t} $$ $$ e^{-it} = \cos{t} - i \sin{t} $$Deze gelijkheden kunnen we herschrijven tot:
$$ \cos{t} = \frac{1}{2}(e^{it} + e^{-it}) $$ $$ \sin{t} = \frac{1}{2i}(e^{it} - e^{-it}) $$De term in de som van de fourierreeks kunnen we hiermee herschrijven naar:
$$ a_n\cos{\omega x} + b_n\sin{\omega x} = \frac{1}{2}a_n(e^{i\omega x}+e^{-i\omega x}) + \frac{1}{2i}b_n(e^{i\omega x}-e^{-i\omega x}) = \frac{1}{2}(a_n - ib_n) e^{i\omega x} - \frac{1}{2}(a_n + ib_n) e^{-i \omega x} $$We definiëren nu de volgende constanten:
$$ c_0 = a_0 $$ $$ c_n = \frac{1}{2}(a_n-ib_n) $$ $$ k_n = \frac{1}{2}(a_n+ib_n) $$De fourierreeks wordt dan:
$$ f(x) = c_0 + \sum_{n=1}^{\infty} (c_n e^{i\omega x} + k_ne^{-i\omega x}) $$Met de formules waarmee we de constanten berekenen, vinden we in deze nieuwe notatie:
$$ c_n = \frac{1}{2}(a_n - ib_n) = \frac{1}{2L} \int_{-L}^L f(x) (\cos{\omega x} - i\sin{\omega x}) dx $$ $$ c_n = \frac{1}{2L} \int_{-L}^L f(x) e^{-i\omega x} dx $$ $$ k_n = \frac{1}{2}(a_n + ib_n) = \frac{1}{2L} \int_{-L}^L f(x) (\cos{\omega x} + i\sin{\omega x}) dx $$ $$ k_n = \frac{1}{2L} \int_{-L}^L f(x) e^{i\omega x} dx $$De formules voor c0, cn en kn hebben nu bijna dezelfde vorm. Het enige verschil tussen cn en kn is het minnetje in de e-macht. Het ligt daarom voor de hand om te definiëren dat kn = c-n. De constanten cn lopen nu dus door van min oneindig tot plus oneindig.
Ook c0 kunnen we op deze manier schrijven:
$$ c_0 = a_0 = \frac{1}{2L} \int_{-L}^L f(x) dx $$ $$ c_0 = \frac{1}{2L} \int_{-L}^L f(x) e^{i\omega x} dx $$We hebben hier gebruikt dat ei&omage;t = 1, omdat als n = 0, dan wordt ω nul.
Onze fourierreeks wordt dus:
De bovenstaande som is alleen geldig voor periodieke functies f(x) met periode 2L. We kunnen de som echter herschrijven, zodat deze ook geldig is voor niet periodieke functies. We doen dit door de L naar oneindig te laten lopen. We gebruiken hiervoor dat:
$$ \Delta \omega = \frac{(n+1)\pi}{L} - \frac{n\pi}{L} = \frac{\pi}{L} $$Als we dit invullen in de bovenstaande formule, dan vinden we:
$$ f(x) = \sum_{n=-\infty}^{\infty} c_n e^{i\omega x} $$ $$ c_n = \frac{\Delta \omega}{2\pi} \int_{-L}^L f(x) e^{-i\omega x} dx $$We halen nu Δω uit de constante en laten dan L naar oneindig lopen. We vinden dan:
$$ f(x) = \int_{-\infty}^{\infty} c_n e^{i\omega x} d\omega $$ $$ c_n = \frac{1}{2\pi} \int_{-\infty}^{\infty} f(x) e^{-i\omega x} dx $$Als we nu ook nog een factor \(1/\sqrt{2\pi}\) uit de constante halen, dan krijgen beide formules zoveel mogelijk dezelfde vorm:
$$ f(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} c_n e^{i\omega x} d\omega = $$ $$ c_n = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} f(x) e^{-i\omega x} dx $$Dit is de meest algemene vorm van de fouriertransformaties. In het geval van het (u,t)-diagram, wordt dit:
$$ u(t) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \hat{u}(\omega) e^{i\omega t} dw $$ $$ \hat{u}(\omega) = \frac{1}{\sqrt{2\pi}} \int_{\infty}^{\infty} u(t) e^{-i\omega t} dt $$