Extra stof hoofdstuk gravitatie
Lagrangiaanse mechanica
De Newtoniaanse mechanica is gebasseerd op de wetten van Newton. In de 19de eeuw ontdekte de briljante wetenschappers Euler, Lagrange en een aantal tijdgenoten dat deze zelfde mechanica ook met een andere basis beschreven kon worden. Deze versie wordt de Lagrangiaanse mechanica genoemd. Deze versie van de mechanica had een aantal voordelen en is het onderwerp van de volgende paragraaf. In deze paragraaf gaan we de wiskunde behandelen die we hiervoor nodig hebben - de zogenaamde variatiecalculus.
De eerste persoon die bezig was met een simpele vorm van variatiecalculus was Fermat. Fermat ontdekte dat als hij een lichtstraal vanaf een willekeurig punt S naar een andere willekeurig punt D wilde schijnen, dat het licht dan altijd het pad nam dat het minste tijd kost. Dit wordt het principe van Fermat genoemd. Dit principe geldt zelfs als punt S zich bijvoorbeeld in de lucht bevindt en punt D onder water. In de onderstaande afbeelding legt het licht tussen punt S en D altijd pad SLD af. Dit pad kost de minste tijd omdat licht sneller voortbeweegt in lucht dan in water. Het scheelt op deze manier een beetje tijd als het licht net iets langer in de lucht blijft bewegen.
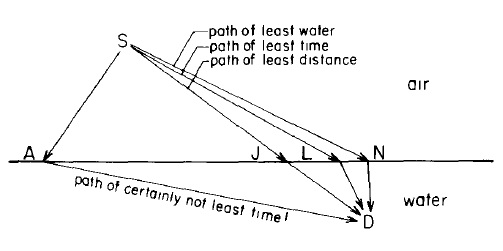
In de tijd van Fermat was het een compleet mysterie waarom licht dit deed. Het leek of het licht van tevoren alle mogelijke paden bestudeerde en dan het pad koos waar de tijdduur het kortst was. Het begrijpen van dit mysterie kwam pas in de 20ste eeuw met de kwantummechanica (hierover later meer).
Omdat licht dus altijd het pad kiest waar de tijd minimaal is, werd het handig om een wiskunde te ontwikkelen waarbij een pad bepaald kon worden waarbij een bepaalde waarde (zoals de tijd) minimaal is. Deze wiskunde wordt de variatiecalculus genoemd.
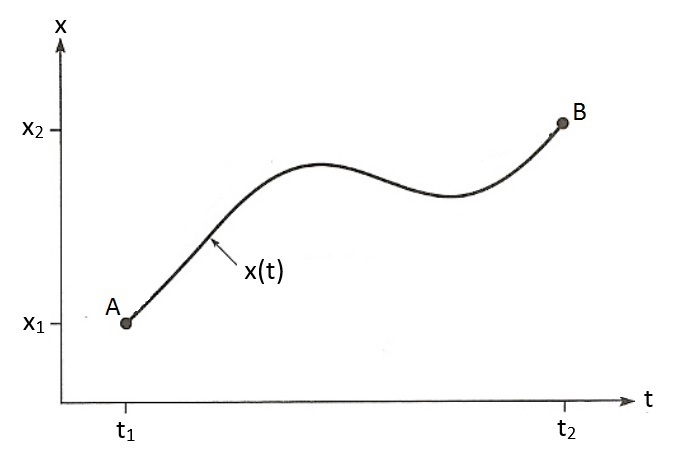
Stel dat een deeltje onder invloed van een aantal krachten beweegt van punt A naar punt B en dat het het pad van het deeltje gegeven wordt door de functie x(t). De beweging start op tijdstip t1 en eindigt op tijdstip t2 (zie de onderstaande afbeelding).
De waarde die we minimaal willen maken noemen we de actie S. In het geval van het principe van Fermat zouden we de S gelijk stellen aan de tijd. We gaan hier echter iets algemener te werk. Het blijkt dat de variatiecalculus werkt voor alle S waarvoor de volgende formule geldt:
$$ S = \int^{t_2}_{t_1} L(x,\dot{x}) dt \;\;\;\; \text{(minimaal)}$$S is hier gelijk aan de integraal over de tijd van een willekeurige functie L die afhankelijk is van x en zijn afgeleide naar de tijd. Als we L gelijkstellen aan 1, dan wordt de integraal gelijk aan de tijd en dan is S gelijk aan t, zoals bij het principe van Fermat, maar hetzelfde principe dat we hier gaan uitwerken geldt dus ook voor heel veel andere uitdrukkingen voor L.
Als S minimaal is, dan betekent dat dat alle nabijgelegen paden \(\tilde{x}\) een grotere waarde voor S moeten hebben.
$$ S = \int^{t_2}_{t_1} L(\tilde{x},\dot{\tilde{x}}) dt \;\;\;\; \text{(niet minimaal)}$$Een nabijgelegen pad definiëren we als volgt:
$$ \tilde{x} = x + \alpha \eta(t) $$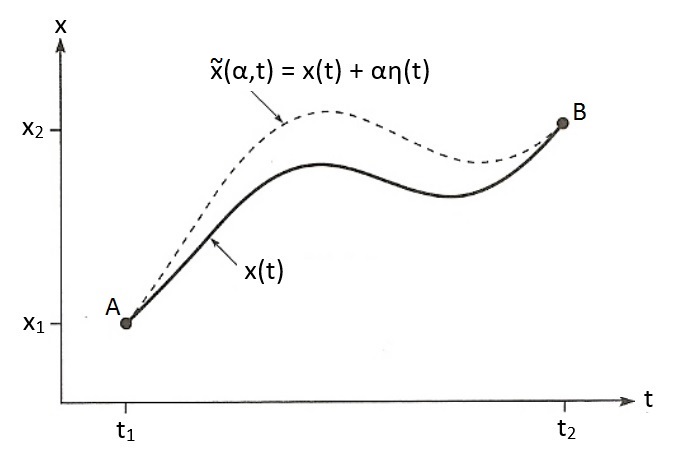
η(t) is een willekeurige functie die als eigenschap heeft dat deze nul is op tijdstip t1 en t2, zodat alle paden wel beginnen in punt A en eindigen in punt B. Er geldt dus:
$$ \eta(t_1) = \eta(t_2) = 0 $$α is hier een constante die we kunnen invullen zoals we willen. Als we α = 0 kiezen, dan krijgen we het oorspronkelijke pad x(t) terug waarbij S minimaal is. Bij een andere α wordt S groter dan het minimum. Als we dus een grafiek zouden maken van de waarde van S bij verschillende α, dan vinden we:
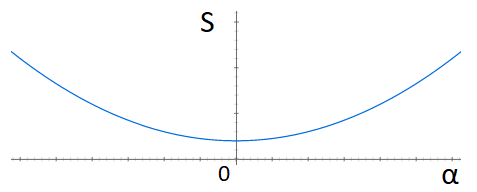
Omdat de grafiek bij α=0 horizontaal loopt, is de helling op dat punt nul. Er geldt dan dus:
$$ \frac{dS}{d\alpha} = 0 \;\;\;\; (\text{als }\alpha = 0)$$Met de definitie van S kunnen we dit uitschrijven tot:
$$ \frac{d }{d\alpha} \int^{t_2}_{t_1} L dt = 0 $$Met de Leibniz-regel kunnen we dit omschrijven tot:
$$ \int^{t_2}_{t_1} \frac{\partial L }{\partial \alpha} dt = 0 $$De afgeleide van L naar α kunnen we met de zogenaamde kettingregel als volgt uitschrijven:
$$ \int^{t_2}_{t_1} \left( \frac{\partial L }{\partial \tilde{x}} \frac{\partial \tilde{x} }{\partial \alpha} + \frac{\partial L }{\partial \dot{\tilde{x}}} \frac{\partial \dot{\tilde{x}} }{\partial \alpha} \right)dt = 0 $$Met behulp van \( \tilde{x} = x + \alpha \eta \) vinden we:
$$ \frac{\partial \tilde{x} }{\partial \alpha} = \eta $$ $$ \frac{\partial \dot{\tilde{x}} }{\partial \alpha} = \dot{\eta} $$Als we deze uitspraken in de bovenstaande uitspraak stoppen, dan vinden we:
$$ \int^{t_2}_{t_1} \left( \frac{\partial L }{\partial \tilde{x}} \eta + \frac{\partial L }{\partial \dot{\tilde{x}}} \dot{\eta} \right)dt = 0 $$Met behulp van partiële integratie kunnen we de tweede term in de integraal herschrijven:
$$ \frac{\partial L }{\partial \dot{\tilde{x}}}\eta(t_2) - \frac{\partial L }{\partial \dot{\tilde{x}}}\eta(t_1) - \int^{t_2}_{t_1} \left( \frac{\partial L }{\partial \tilde{x}} \eta - \frac{d}{dt}\frac{\partial L }{\partial \dot{\tilde{x}}} \eta \right) dt = 0 $$Omdat η(t1) = η(t2) = 0, vallen de eerste twee termen weg. We houden dus over dat:
$$ \int^{t_2}_{t_1} \left( \frac{\partial L }{\partial \tilde{x}} \eta - \frac{d}{dt}\frac{\partial L }{\partial \dot{\tilde{x}}} \eta \right) dt = 0 $$Als we nu η buiten haakjes halen, dan vinden we:
$$ \int^{t_2}_{t_1} \left( \frac{\partial L }{\partial \tilde{x}} - \frac{d}{dt}\frac{\partial L }{\partial \dot{\tilde{x}}} \right) \eta dt = 0 $$Om deze integraal daadwerkelijk nul te maken, moet of het deel tussen de haken of η(t) gelijk zijn aan nul. η(x) is echter een willekeurige functie, die we zelf kunnen kiezen en is dus niet noodzakelijk gelijk aan nul. De term tussen haakjes moet dus nul worden. Er geldt dus:
$$ \frac{\partial L }{\partial \tilde{x}} - \frac{d}{dt}\frac{\partial L }{\partial \dot{\tilde{x}}} = 0$$Bij α = 0 wordt dit:
$$ \frac{\partial L }{\partial x} - \frac{d}{dt}\frac{\partial L }{\partial \dot{x}} = 0$$Dit wordt de Euler-Lagrange vergelijking genoemd. Deze vergelijking vertelt ons dat L een minimale S oplevert als aan deze vergelijking voldaan wordt.
In de vorige paragraaf hebben we bewezen dat als een functie L voldoet aan de onderstaande Euler-Lagrange vergelijking, dat de functie S dan een minimale waarde heeft.
$$ \frac{\partial L }{\partial x} - \frac{d}{dt}\frac{\partial L }{\partial \dot{x}} = 0$$In de vorige paragraaf hebben we gezien dat in het geval van licht de tijd geminimalizeerd werd. Na behoorlijk wat zoeken vond men dat er ook een L te vinden was voor deeltjes met een massa. Deze L bleek gelijk te zijn aan:
$$ L = E_{kin}-E_{pot}(x) $$Dit gaan we bewijzen door te checken dat deze L voldoet aan de Euler-Lagrange vergelijking:
$$ \frac{\partial (E_{kin}-E_{pot}) }{\partial x} - \frac{d}{dt}\frac{\partial (E_{kin}-E_{pot}) }{\partial \dot{x}} = 0$$Omdat de kinetische energie niet afhankelijk is van x en de potentiele energie niet van ẋ, kunnen we dit simpeler schrijven als:
$$ - \frac{\partial E_{pot} }{\partial x} - \frac{d}{dt}\frac{\partial E_{kin} }{\partial \dot{x}} = 0$$In de paragraaf over de behoudswetten vonden we dat:
$$ -\frac{\partial E_{pot} }{\partial x} = F $$Ook geldt dat:
$$ \frac{d}{dt}\frac{\partial E_{kin} }{\partial \dot{x}} = \frac{d}{dt}(m\dot{x}) = m\ddot{x} $$De Euler-Lagrangevergelijking kan nu dus verder versimpeld worden tot:
$$ F = m\ddot{x} $$En dit is de tweede wet van Newton! De tweede wet van Newton rolt dus automatisch uit de Euler-Lagrangevergelijking als we kiezen voor L = Ekin-Epot. Omdat we de Euler-Lagrangevergelijking met deze L hebben kunnen omschrijven tot de tweede wet van Newton, zeggen was dat beide formules equivalent aan elkaar zijn. We zeggen ook wel dat de Newtoniaanse mechanica en de Lagrangiaanse mechanica equivalent aan elkaar zijn.
Wat hebben we hier dus gevonden? We hebben laten zien dat met L = Ekin-Epot voldaan wordt aan de Euler-Lagrange vergelijking. Als gevolg kunnen we concluderen dat deeltjes in de natuur altijd het pad volgen waarbij de actie S die hoort bij deze Lagrangiaan minimaal is. Als we van alle mogelijke paden die een deeltje aflegt de actie zouden bepalen, dan zou de actie het laagst zijn voor het pad dat het deeltje daadwerkelijk aflegt. Dit wordt het principe van principe van Hamilton genoemd:
'Voor alle mogelijke paden \( \tilde{x}(t) \) waarlangs een voorwerp kan bewegen van punt A naar punt B in een bepaald tijdsinterval, is het werkelijke pad \( x(t) \) het pad waarbij de tijdsintegraal van het verschil tussen de kinetische en de potentiële energie minimaal is'.
Voorbeelden
Laten we beginnen met een aantal voorbeelden waarvan we de antwoorden al kennen vanuit de Newtoniaanse mechanica, zodat we gemakkelijk kunnen checken of we het juiste antwoord gevonden hebben. Neem bijvoorbeeld het blokje dat horizontaal heen en weer beweegt aan een veer over een wrijvingsloos oppervlak. De Lagrangiaan wordt in dit geval:
$$ L = E_{kin} - E_{pot} = \frac{1}{2}m\dot{x}^2 - \frac{1}{2}Cx^2 $$Met deze L werken we nu de Euler-Lagrangevergelijking uit:
$$ \frac{\partial L }{\partial x} - \frac{d}{dt}\frac{\partial L }{\partial \dot{x}} = 0$$ $$ \frac{\partial L }{\partial x} = -Cx $$ $$ \frac{\partial L }{\partial \dot{x}} = m\dot{x} $$ $$ \frac{d}{dt}\frac{\partial L }{\partial \dot{x}} = m\ddot{x} $$De Euler-Lagrangevergelijking wordt dus:
$$ m\ddot{x} = -Cx $$Dit is precies de vergelijking die we in het paragraaf over de Newtoniaanse mechanica gebruikt hadden om een oplossing te vinden voor de beweging van het blokje.
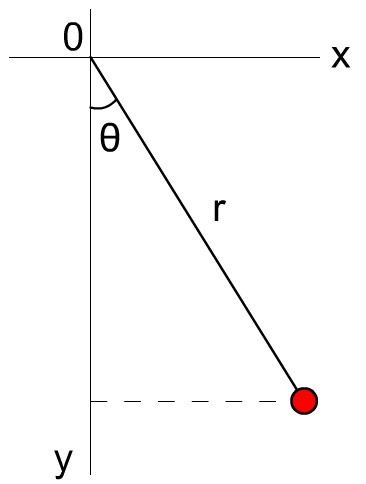
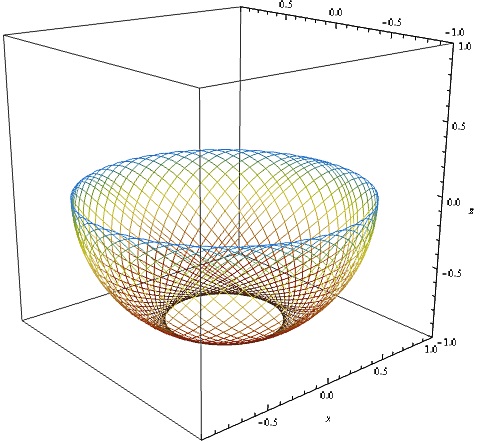
Nog een laatste voorbeeld. Dit voorbeeld is een stuk lastiger en het is niet nodig dit geheel te volgen, maar laat zien hoe krachtig de methode is. Neem een puntmassa m die beweegt in een bolvormige schaal. De oorspong plaatsen we in het centrul van de bol, zodat de radiusvector altijd dezelfde lengte l heeft. De Lagrangiaan wordt in dit geval:
$$ L = \frac{1}{2}mv^2 - mgz $$Vanwege de bolvorm is het handig om bolcoördinaten te gebruiken.
$$ L = \frac{m l^2}{2}(\dot{\theta}^2+\dot{\phi}^2\sin^2\theta) + mgl\cos\theta $$We kunnen nu de Euler-Lagrange vergelijking oplossen voor zowel θ en φ:
$$ \frac{\partial L}{\partial \theta} - \frac{\text{d}}{\text{d} t}\frac{\partial L}{\partial\dot{\theta}} = 0 $$ $$ \ddot{\theta}=\dot{\phi}^2\sin\theta\cos\theta-\frac{g}{l}\sin\theta $$ $$ \frac{\partial L}{\partial \phi} - \frac{\text{d}}{\text{d} t}\frac{\partial L}{\partial\dot{\phi}} = 0 $$ $$ \ddot{\phi}=-2\dot{\theta}\dot{\phi}\cot\theta $$Als we deze vergelijkingen oplossen met een computerprogramma, dan vinden we de volgende beweging:
 Rekenen met de Euler-Lagrangevergelijking
Rekenen met de Euler-Lagrangevergelijking
|
|
Met behulp van de Lagrangiaanse mechanica werd in de 20ste eeuw door Emma Noether ontdekt waar behoudswetten vandaan komen. Einstein noemde haar de belangrijkste vrouw in de geschiedenis van de wiskunde. In deze paragraaf gaan we haar theorie bestuderen.
We beginnen met een Lagrangiaan L(q̄,q̄̇). q̄ is hier gelijk aan:
$$ \bar{q}(\alpha,t) = q + \alpha $$q is hier een willekeurige variabele waar de Lagrangiaan van afhankelijk is en α is een constante.
De afgeleide van de Lagrangiaan naar α wordt met behulp van de kettingregel:
$$ \frac{dL }{d\alpha } = \frac{\partial L }{\partial \bar{q}} \frac{d\bar{q}}{d\alpha} + \frac{\partial L}{\partial \dot{\bar{q}}} \frac{d\dot{\bar{q}}}{d\alpha} $$Deze uitspraak kunnen we versimpelen door uit te werken dat:
$$ \frac{d\bar{q}}{d\alpha} = 1 $$ $$ \frac{d\dot{\bar{q}}}{d\alpha} = 0 $$De vergelijking wordt:
$$ \frac{dL }{d\alpha } = \frac{\partial L }{\partial \bar{q}} $$Als we deze vergelijking in de Euler-Lagrangevergelijking stoppen, dan vinden we:
$$ \frac{dL }{d\alpha } = \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{\bar{q}}} \right) $$Stel dat de afgeleide van L naar α gelijk is aan nul, dan vinden we:
$$ \frac{\partial L}{\partial \dot{\bar{q}}} = \text{constant} \;\;\;\;\; \left(\text{als } \frac{dL}{d\alpha}=0 \right)$$Als de afgeleide van L naar α dus nul is, dan hebben we een behouden grootheid gevonden. Dit wordt Noether's theorema genoemd. Om het belang hiervan te zien bespreken we een aantal voorbeelden.
Voorbeelden
Stel we gooien een steen onder een willekeurige hoek omhoog. We verwaarlozen de wrijvingskracht. De lagrangiaan wordt in dat geval:
$$ L(x) = \frac{1}{2}m\dot{x}^2 + \frac{1}{2}m\dot{y}^2- mgy $$Stel nu dat we nu exact dezelfde worp herhalen, maar nu niet op positie x, maar op positie x̄ = x + α. De Lagrangiaan word dan:
$$ L(\bar{x}) = \frac{1}{2}m \dot{\bar{x}}^2 + \frac{1}{2}m\dot{y}^2 - mgy $$Er geldt dat:
$$ \dot{\bar{x}} = \frac{d(x+\alpha)}{dt} = \dot{x}$$Deze Lagrangiaan kan dus ook herschreven worden tot:
$$ L(\bar{x}) = \frac{1}{2}m\dot{x}^2 + \frac{1}{2}m\dot{y}^2 - mgy $$Maar dit is dezelfde Langrangiaan als L(x)! De Lagrangiaan blijft dus onveranderd als we x vervangen door x + α. We noemen deze eigenschap ook wel translatie symmetrie.
Dankzij deze symmetrie is de lagrangiaan dus niet afhankelijk van α en geldt dat dL/dα = 0. Dit was een voorwaarde voor het toepassen van Noether's theorema. Als gevolg moet er dus een behouden grootheid zijn gegeven door:
$$ \frac{\partial L}{\partial \dot{\bar{x}}} = m\dot{\bar{x}} = m\dot{x}= p = \text{constant}$$We hebben hier behoud van impuls gevonden! Het behoud van impuls volgt dus direct uit de translatiesymmetrie. Behoud van impuls is dus een gevolg van het feit dat een experiment op verschillende locaties hetzelfde resultaat kan geven!
Op soortelijke wijze kan je voor alle symmetrieën van de Lagrangiaan een bijbehorende behouden grootheid vinden.
Laten we nu rotatiesymmetrie bestuderen. Een voorbeeld van een rotatiesymmetrisch is het gravitatieveld om een bolvormige planeet. De Lagrangiaan voor dit systeem is:
$$ L = \frac{1}{2}mv^2 + \frac{GMm}{r}$$In poolcoördinaten wordt dit:
$$ L(\theta) = \frac{1}{2}m(r^2 + r^2\dot{\theta}^2) + \frac{GMm}{r} $$Stel dat we op deze bolvormige planeet een steen omhoog zouden gooien starten bij een bepaalde hoek θ en stel dat we dit experiment daarna herhalen, maar dan startend bij hoek \(\bar{\theta}\) = θ + α. We vinden dan:
$$ L(\bar{\theta}) = \frac{1}{2}m(r^2 + r^2 \dot{\bar{\theta}}^2) + \frac{GMm}{r} = $$ $$\frac{1}{2}m(r^2 + r^2\dot{\theta}^2) + \frac{GMm}{r} $$Ook hier vinden we dus dezelfde Lagrangiaan terug en als gevolg geldt dL/dα = 0 en hebben we dus weer een behouden grootheid:
$$ \frac{\partial L}{\partial \dot{\bar{\theta}}} = mr^2\dot{\bar{\theta}} = mr^2\dot{\theta} = J = \text{constant}$$Dit is het behoud van impulsmoment! We zien hier dus dat het impulsmoment behouden is dankzij rotatiesymmetrie.
De laatste symmetrie die we gaan bespreken is de tijdsymmetrie. De natuurkunde blijft onveranderderd als we eenzelfde process op een later tijdstip uitvoeren. De standaard methode werkt echter niet voor de tijd. Noether's theorema wordt in dit geval:
$$ \frac{\partial L}{\partial \dot{\bar{t}}} = \text{constant}$$De afgeleide van de tijd naar de tijd die in de noemen van de breuk te vinden is, is echter 1 en dit maakt deze vergelijking waardeloos.
Er is echter een andere manier om met tijdsymmetrie te werken. We gaan hiervoor eerst aantonen dat voor de totale energie geldt dat:
$$ E_{tot} = \frac{\partial L}{\partial \dot{x}}\dot{x} - L $$We kunnen dit laten zien door de lagrangiaan uit te werken:
$$ E_{tot} = \frac{\partial (E_{kin}-E_{pot})}{\partial \dot{x}}\dot{x} - (E_{kin}-E_{pot}) $$ $$ E_{tot} = \frac{\partial E_{kin}}{\partial \dot{x}}\dot{x} - (E_{kin}-E_{pot}) $$ $$ E_{tot} = m\dot{x}^2 - (E_{kin}-E_{pot}) $$De eerste term is gelijk aan twee keer de kinetische energie. Als we dit invullen, dan vinden we:
$$ E_{tot} = 2E_{kin} - E_{kin} + E_{pot} $$ $$ E_{tot} = E_{kin} + E_{pot} $$Dit is inderdaad de gebruikelijk uitspraak voor de totale energie!
Als we de afgeleide van de energie naar de tijd nemen voor onze nieuwe definitie van de energie, dan vinden we:
$$ \frac{dE}{dt} = \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\dot{x}\right) - \frac{dL}{dt} $$Als we de productregel toepassen op de eerste term, dan vinden we:
$$ \frac{dE}{dt} = \left(\frac{d}{dt} \frac{\partial L}{\partial \dot{x}} \right)\frac{dx}{dt} + \frac{\partial L}{\partial \dot{x}}\frac{d\dot{x}}{dt} - \frac{dL}{dt} $$Als we de kettingregel toepassen op de laatste term en de mogelijkheid open houden dat L ook expliciet van t afhankelijk is, dan vinden we:
$$ \frac{dE}{dt} = \left(\frac{d}{dt} \frac{\partial L}{\partial \dot{x}} \right)\frac{dx}{dt} + \frac{\partial L}{\partial \dot{x}}\frac{d\dot{x}}{dt} - \frac{\partial L}{\partial x}\frac{dx}{dt} - \frac{\partial L}{\partial \dot{x}}\frac{d\dot{x}}{dt} - \frac{\partial L}{\partial t} $$De tweede en de vierde term vallen direct tegen elkaar weg. Met de Euler-Lagrangevergelijking vallen de eerste en de derde ook tegen elkaar weg. We houden dus over dat:
$$ \frac{dE}{dt}=-\frac{\partial L}{\partial t} $$We zien hier dat als de partiële afgeleide van de lagrangiaan naar de tijd nul is, dat dan de energie behouden is:
$$ E = \text{constant} \;\;\;\;\; \left(\text{als } \frac{\partial L}{\partial t} = 0 \right)$$Aangezien we tot nu toe nog nooit een lagrangiaan hebben gezien die direct afhankelijk was van de tijd, moeten we dus in al deze gevallen concluderen dat de energie behouden is. Energiebehoud volgt dus uit het tijdsymmetrie.
Later in dit hoofdstuk zullen we zien dat op soortgelijke manier te bewijzen is dat lading behouden blijft. Dit is het gevolg van een symmetrie in de natuurwetten voor elektromagnetische velden genaamd de gauge-symmetrie. In kwantummechanica kunnen we laten zien dat de kans een deeltje aan te treffen behouden blijft.