Extra stof hoofdstuk kwantummechanica
De Schrödingervergelijking
De theorie van Bohr kon het waterstof veel beter beschrijven dan de theorie van Newton, maar na verloop van tijd werd toch gevonden dat de theorie niet helemaal overeenkwam met de realiteit. Daarnaast werkte de methode helemaal niet bij atomen complexer dan waterstof. De theorie van Bohr was dus een goede eerste stap, maar nog niet het hele verhaal.
De volgende stap was de zogenaamde Schrödingervergelijking. Een algemene golfvergelijking waarmee we de beweging van kwantumgolven kunnen beschrijven. We gebruiken voor de kwantumgolf het symbool Ψ. We noemen dit ook wel de golffunctie.
In deze paragraaf zullen we laten zien hoe we deze formule kunnen vinden op basis van deze eerder gevonden eigenschappen van de kwantumgolf:
$$ p = h/\lambda $$ $$ E = hf $$Om formules in de rest van het hoofdstuk iets te versimpelen, gaan we deze formules iets anders schrijven met behulp van ℏ=h/(2π), k = 2π/λ en ω = 2πf. We vinden hiermee:
$$ p = \hbar k $$ $$ E = \hbar\omega $$In de Newtoniaanse mechanica heeft elk deeltje kinetische en potentiële energie. Er geldt dus:
$$ E = E_{kin} + E_{pot} $$ $$ E = \frac{p^2}{2m} + E_{pot} $$Als we in deze formule de kwantummechanische formules \(p = \hbar k \) en \(E = \hbar\omega\) invullen, dan vinden we de kwantummechanische formule voor de energie:
$$ \frac{\hbar^2k^2}{2m} + E_{pot} = \hbar\omega $$Om zijn golfvergelijking te vinden, koos Schrödinger een simpel sinusvormig golfje om zijn vergelijkingen mee te testen. De algemene formule voor een stilstaande sinusvormige golf met golflengte λ wordt gegeven door:
$$ \Psi = \sin{ \left( \frac{2\pi x}{\lambda} \right)} $$Als we ook nog willen dat dit golfje naar rechts gaat bewegen, dan vervangen we 'x' door 'x - vt'. Als de tijd t nu toeneemt, dan start de sinus een steeds grotere x. We vinden dan:
$$ \Psi = \sin{ \left( \frac{2\pi}{\lambda} (x - vt)\right)} $$Met v = fλ kunnen we dit herschrijven tot:
$$ \Psi = \sin{ \left( \frac{2\pi x}{\lambda} - 2\pi ft \right)} $$Met k = 2π/λ en ω = 2πf versimpelt dit tot:
$$ \Psi = \sin{ (kx - \omega t)} $$Schrödinger ging toen op zoek naar een golfvergelijking die met het bovenstaande golfje de kwantummechanische energie van het deeltje zou teruggeven. Zijn eerste gok was:
$$ - \frac{\hbar^2}{2m} \frac{\partial^2 \Psi}{\partial x^2} + E_{pot}\Psi = \hbar \frac{\partial \Psi}{\partial t} $$Als we het testgolfje namelijk in deze vergelijking stoppen, dan levert de tweede afgeleide naar de plaats aan de linkerkant een extra factor k2 en de eerste afgeleide naar de tijd aan de linkerkant een extra factor ω. Deze factoren komen ook voor in onze energievergelijking. We vinden:
$$ \frac{\hbar^2k^2}{2m} \sin{(kx - \omega t)} + \sin{(kx - \omega t)}E_{pot} = \hbar \omega\cos{(kx - \omega t)} $$Deze vergelijking lijkt lichtelijk op de energievergelijking, maar probleem is dat we de cosinus en sinussen niet kunnen wegstrepen. We komen dus niet op de kwantummechanische energievergelijking uit zoals Schrödinger gehoopt had. Dit pad liep dus dood.
Omdat de sinus in de golffunctie niet werkte, gebruikte Schrödinger een e-macht. De afgeleide van ex naar is is namelijk wederom ex en als deze e-machten onverandert blijven, kunnen we ze na het differentiëren wel wegstrepen. Een golf die hieraan voldoet is:
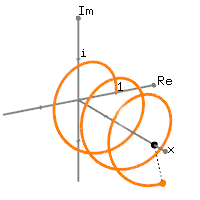
$$ \Psi = e^{i(kx-\omega t)} $$Om te begrijpen wat we hier zien is het handig eerst een voorstelling te maken van eix. Deze formule beschrijft een spiraal met straal 1 in de imaginaire ruimte (zie de onderstaande afbeelding). Door de extra term '-ωt' in de macht gaat beweegt deze spiraal ook nog eens langs de x-as vooruit.
De Schrödingervergelijking die hier het juiste resultaat levert is:
$$ - \frac{\hbar^2}{2m} \frac{\partial^2\Psi}{\partial x^2} + E_{pot}\Psi = i\hbar \frac{\partial \Psi}{\partial t} $$Als we de golffunctie invullen, dan vinden we:
$$ \frac{\hbar^2k^2}{2m} e^{i(kx-\omega t)} + E_{pot} e^{i(kx-\omega t)} = \hbar \omega e^{i(kx-\omega t)} $$Na het wegstrepen van de e-macht, vinden we:
$$ \frac{\hbar^2k^2}{2m} + E_{pot} = \hbar \omega $$Dit is de correcte energievergelijking. De Schrodingervergelijking wordt dus:
$$ - \frac{\hbar^2}{2m} \frac{\partial^2\Psi}{\partial x^2} + E_{pot}\Psi = i\hbar \frac{\partial \Psi}{\partial t} $$Dit komt allemaal mooi uit, maar we hebben hier wel iets heel vreemds moeten aannemen. Onze kwantumgolfjes roteren in de imaginaire ruimte! Hoe vreemd dit ook klinkt, zullen we verder in dit hoofdstuk zien dat we met deze vergelijking het hele periodieke systeem kunnen afleiden.
////////////In de vorige paragraaf hebben we de schrodingervergelijking gevonden. Deze vergelijking heeft de vorm van een golfvergelijking. De golf Ψ kan stromen van plek naar plek. Om dit te beschrijven is het handig even te denken aan het stromen van ladingen. Stel we bestuderen een stukje van een stroomdraad met volume dV en lengte dx. De volgende formule vertelt ons dat de verandering van de hoeveelheid lading in het lijnstukje in tijdstapje dt gelijk moet zijn aan de lading die via de twee zijden is toegestroomt of weggestroomd.
$$ \frac{dQ}{dt} = I_L - I_R = dI $$We gaan nu Q en I iets anders schrijven. Net als dat we de massa kunnen schrijven als dm = ρdV, kunnen we de lading schrijven als dq = ρdV. ρ is in dit geval gelijk aan de ladingsdichtheid (in C/m3). De stroom door oppervlak dA kunnen we ook schrijven als dI = JdA, waarbij J de stroomdichtheid is (in A/m2). Met deze definities vinden we:
$$ \frac{d\rho}{dt}dV = dJdA $$Dit kunnen we herschrijven tot:
$$ \frac{d\rho}{dt}dxdydz = dJdydz $$ $$ \frac{d\rho}{dt}dx = dJ $$ $$ \frac{d\rho}{dt} = \frac{dJ}{dx} $$We noemen dit de continuiteitsvergelijking. We kunnen een dergelijke vergelijking ook voor de schrodingervergelijking opstellen. Hier nogmaals de vergelijking:
$$ i\partial_t \Psi = -\frac{\hbar}{2m}\partial_x^2 \Psi + E_{pot}\Psi $$Ook hebben we de complexgeconjugeerde van deze vergelijking nodig hebben. Dit is dezelfde vergelijking, maar elke i wordt nu veranderd in -i. De complexgeconjugeerde van de golffunctie zelf schrijven we als Ψ*. We vinden dan:
$$ -i\partial_t \Psi^* = -\frac{\hbar}{2m}\partial_x^2 \Psi^* + E_{pot}\Psi^* $$Voor een reden die later duidelijk wordt, vermenigvuldigen we de eerste vergelijking met Ψ* en de tweede vergelijking met Ψ en dan tellen we beide termen van elkaar af. We vinden dan:
$$ -\frac{\hbar}{2m}(\Psi^*\partial_x^2\Psi - \Psi\partial_x^2\Psi^*) = i(\Psi^* \partial_t\Psi - \Psi \partial_t\Psi^*) $$Dit kunnen we met de kettingregel herschrijven tot:
$$ -\frac{\hbar}{2m} \partial_x (\Psi^*\partial_x\Psi - \Psi\partial_x\Psi^*) = i \partial_t (\Psi^*\Psi) $$Als we beide zijden met -i vermenigvuldigen, dan vinden we:
$$ \partial_x \left( i\frac{\hbar}{2m} (\Psi^*\partial_x\Psi - \Psi\partial_x\Psi^*) \right) = \partial_t (\Psi^*\Psi) $$We hebben nu een formule gevonden in de vorm van de continuiteitsvergelijking (aan de ene zijde hebben we een afgeleide naar x en aan de andere de afgeleide naar t). De term Ψ*Ψ speelt hier de rol van de ladingsdichtheid. Maar wat voor een dichtheid is Ψ*Ψ eigelijk? Wat is hier precies aan het stromen? Het antwoord op deze vraag kunnen we niet afleiden, maar uit metingen blijkt dat dit gelijk is aan de kansdichtheid. Het is de kans dat je het deeltje op een bepaalde positie vindt.
De kans om een deeltje tussen positie A en B aan te treffen wordt gegeven door:
$$ P_{ab}= \int_{a}^{b} \Psi^*\Psi dx $$De kans om het deeltje in de volledige ruimte aan te treffen moet natuurlijk 100% zijn. Als we intergreren over de hele ruimte vinden we dus altijd het antwoord 1:
$$ P = \int^{\infty}_{-\infty} \Psi^*\Psi dx = 1 $$Operatoren
Omdat een golfje vaak geen precieze locatie heeft, maar is uitgespreid over de ruimte, kunnen we ook niet spreken van de positie van het golfje. We kunnen echter wel spreken van de gemiddelde positie. Deze gemiddelde waarde komt overeen met de gemiddelde positie waar je het deeltje in zal vinden.
Om een formule hiervoor op te stellen moeten eerst even iets leren over kanzen. Stel dat we een groep mensen hebben met verschillende leeftijden. De kans dat een persoon leeftijd L heeft, noteren we als P(L). Als N(L) gelijk is aan het aantal personen met leeftijd L, dan wordt deze kans:
$$ P(L) = \frac{N(L)}{N_{tot}} $$Als we de gemiddelde leeftijd willen bepalen, dan tellen we alle leeftijden bij elkaar op en delen we door het totaal aantal leerlingen. De optelling van alle leeftijden wordt gegeven door:
$$ \sum_L{N(L)L} $$Het gemiddelde wordt dus gegeven door:
$$ \langle L \rangle = \frac{\sum_L{N(L)L}}{N_{tot}} = \Sigma_L LP(L) $$Op dezelfde manier vinden we voor de gemiddelde positie van de kwantumgolf:
$$ \langle x \rangle = \int_{-\infty}^\infty x P(x) dx $$We kunnen dit uitschrijven tot:
$$ \langle x \rangle = \int_{-\infty}^\infty \Psi^* x \Psi dx $$Als we deze formule afleiden naar de tijd, dan kunnen we ook de gemiddelde waarde van de snelheid van de golf vinden:
$$ \langle v \rangle = \frac{d\langle x \rangle}{dt} $$In het extra stuk onder aan de paragraaf wordt deze vergelijking uitgewerkt. Het resultaat hier van is:
$$ \langle v \rangle = \int \Psi^* \left( - \frac{i\hbar}{m} \partial_x \right) \Psi dx $$Als we deze vergelijking met 'm' vermenigvuldigen, dan vinden we de gemiddelde impuls:
$$ \langle p \rangle \int \Psi^*\left( -i\hbar \partial_x \right) \Psi dx$$Met de impuls kunnen we de gemiddelde energie van de kwantumgolf vinden:
$$ \langle E \rangle = \left\langle \frac{p^2}{2m} + V \right\rangle = \int \Psi^* \left(-\frac{\hbar^2}{2m} \partial_x^2 + V \right) \Psi dx $$Zoals je wellicht is opgevallen, staat er bij elke formule voor de gemiddelde van de kwantumgolf een factor tussen de Ψ* en Ψ in de integraal. We noemen deze factor de operator. Voor de positie, de impuls en de energie gelden dus de volgende operatoren:
$$ \hat{x} = x $$ $$ \hat{p} = \frac{\hbar}{i}\partial_x $$ $$ \hat{E} = -\frac{\hbar^2}{2m} \partial_x^2 + V $$ /////////////EXTRA EXTRADe gemiddelde snelheid van de kwantumgolf wordt gegeven door:
$$ \langle v \rangle = \frac{d\langle x \rangle}{dt} = \int_{-\infty}^\infty \partial_t(\Psi^* x \Psi) dx $$In de laatste stap hebben gebruik gemaakt van de Leibniz regel. Deze regel vertelt ons dat als we een totale afgeleide binnen de integraal willen halen, dat dit dan verandert in een partiële afgeleide.
De afgeleide in deze integraal kunnen we uitschrijven als:
$$ \partial_t (\Psi^*\Psi) = \Psi^*\partial_t \Psi + \partial_t \Psi^* \Psi $$Als we de Schrödingervergelijking omschrijven, dan vinden we:
$$ \partial_t \Psi = \frac{i\hbar}{2m}\partial^2_x \Psi - iV\Psi $$Als we deze formule substitueren in de voorgaande formule, dan vinden we:
$$ \partial_t (\Psi^*\Psi) = \frac{i\hbar}{2m} ( \Psi^*\partial_x^2\Psi - \partial_x^2 \Psi^* \Psi ) = \frac{i\hbar}{2m} \partial_x ( \Psi^*\partial_x\Psi - \partial_x \Psi^* \Psi ) $$De gemiddelde waarde van v wordt dus:
$$ \langle v \rangle = \frac{i\hbar}{2m}\int x \partial_x ( \Psi^*\partial_x\Psi - \partial_x \Psi^* \Psi )dx $$Met partiële integratie vinden we:
$$ \langle v \rangle = - \frac{i\hbar}{2m}\int ( \Psi^*\partial_x\Psi - \partial_x \Psi^* \Psi )dx $$De randtermen zijn hier nul geworden, omdat de golffunctie in de oneindigheid gelijk wordt aan nul. Een tweede partiële integratie toegepast op de tweede term geeft:
$$ \langle v \rangle = - \frac{i\hbar}{m}\int \Psi^*\partial_x\Psi dx $$Dit is inderdaad gelijk aan het antwoord uit de paragraaf.
De tijdsonafhankelijke Schrödingervergelijking
In deze paragraaf gaan we de Schrödingervergelijking oplossen voor een deeltje in een één dimensionaal doosje. We zullen zien dat we hiermee dezelfde formule afleiden die we ook in het hoofdstuk kwantummechanica gezien hebben.
We beginnen door de formule nog een keer op te schrijven:
$$ - \frac{\hbar^2}{2m} \frac{\partial^2\Psi}{\partial x^2} + E_{pot}\Psi = i\hbar \frac{\partial \Psi}{\partial t} $$De algemene oplossing hiervan is:
$$ \Psi(x,t) = \psi (x) e^{-iEt/\hbar} $$Als we de bovenstaande vergelijking voor Ψ in de Schrodingervergelijking stoppen, dan vinden we:
$$ - \frac{\hbar^2}{2m} \frac{d^2\psi}{dx^2} + E_{pot}\psi = E\psi $$Dit wordt ook wel de tijdsonafhankelijke Schrödingervergelijking genoemd. De vergelijking is een stuk gemakkelijker op te lossen dan de normale schrodingervergelijking, omdat deze vergelijking geen afgeleide naar de tijd meer heeft.
Deeltje in doos
Het simpelste voorbeeld van een staande kwantumgolf is een deeltje in een doosje. We nemen een doos met oneindig sterke wanden. Als gevolg weten we de golffunctie bij de wanden nul is (het deeltje kan zich immers niet in de wand bevinden). Als we de wanden van de doos plaatsen op x = 0 en x = L, dan geldt dus:
$$ \psi_{x=0} = 0 \;\;\;\;\; en \;\;\;\;\; \psi_{x=L} = 0 $$Het deeltje in de doos heeft alleen kinetische energie en geen potentiele energie. De tijdsonafhankelijke Schrödingervergelijking wordt hiermee:
$$ - \frac{\hbar^2}{2m} \frac{d^2\psi}{dx^2} = E\psi $$De oplossing van deze vergelijking is:
$$ \psi = A\sin{\left( \frac{\sqrt{2mE}}{\hbar} x \right)} + B \cos{\left( \frac{\sqrt{2mE}}{\hbar} x \right)} $$A en B zijn hier constanten waarvan we de waarden nog moeten bepalen. Als we x=0 invullen in de oplossing, dan vinden we:
$$ \psi_{x=0} = B $$Omdat we eerder hadden gezien dat ψ nul moet zijn op positie x=0, moet dus gelden dat:
$$ B = 0 $$We kunnen de oplossing dus versimpelen tot:
$$ \psi_{x=0} = A\sin{\left( \frac{\sqrt{2mE}}{\hbar} x \right)} $$Als we invullen dat x = L, dan vinden we:
$$ A\sin{\left( \frac{\sqrt{2mE}}{\hbar} L \right)} = 0 $$We zouden deze vergelijking kunnen oplossen door A = 0 te kiezen, maar dan wordt onze hele golffunctie ψ nul en als gevolg wordt de kans om het deeltje ergens aan te treffen ook nul. Dit kan niet kloppen. Omdat geldt dat sin(nπ)=0, wordt deze vergelijking ook nul als:
$$ \psi_{x=L} = \frac{\sqrt{2mE}}{\hbar} L = n\pi \;\;\;\; n=1,2,3,... $$n kan hier niet gelijk aan nul zijn, want dan wordt wederom de hele golffunctie nul en hebben we nul procent kans het deeltje ergens te vinden.
Als de deze formule omschrijven, dan vinden we de al bekende formule voor de kinetische energie van het deeltje in de doos:
$$ E_n = \frac{n^2h^2}{8mL^2} \;\;\;\; n=1,2,3,... $$Merk op dat een deeltje in een doos altijd kinetische energie hebben, want zelfs bij n=1 heeft het deeltje energie. Dit betekent dat het elektron in het doosje nooit stil kan staan. Het heeft altijd een beetje kinetische energie. We noemen dit de nulpuntsenergie.
Met deze nieuwe formule voor de energie kunnen we de golffunctie schrijven als:
$$ \psi = A \sin{\frac{n\pi x}{L}} \;\;\;\; n=1,2,3,... $$De bijbehorende kansverdeling wordt:
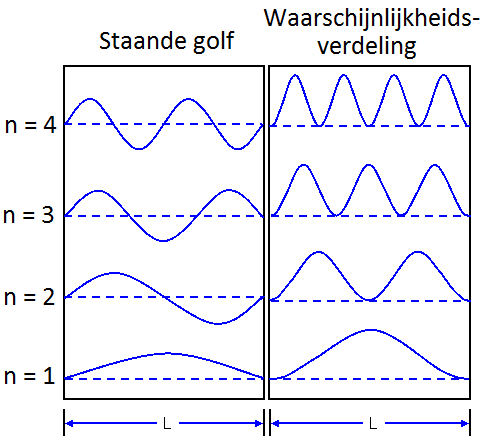
$$ P = \psi^*\psi = A^2\sin{^2\frac{n\pi x}{L}} $$Hieronder zien de afbeeldingen van zowel de golffunctie als de kansverdeling voor verschillende n. We vinden links de staande golven die we hadden verwacht. Rechts zien we dat de kansverdeling altijd positief is. Dit komt goed uit, omdat een negatieve kans immers geen betekenis heeft.
We kunnen nu voor de volledigheid ook de volledige oplossing Ψ opschrijven. We gebruiken hiervoor dat \(\Psi = \psi (x) e^{-iEt/\hbar} \):
$$ \Psi = A \sin{\frac{n\pi x}{L}} e^{-iEt/\hbar} \;\;\;\; n=1,2,3,... $$We vinden hier dezelfde golven als in de bovenstaande oplossing, maar plaats dat de staande golven op en neer bewegen zoals bij een snaar, roteren ze rond in de imaginaire ruimte.
Ook geldt dat:
$$ \int \psi_m^*\psi_n dx = \delta_{mn}$$Rechts van de vergelijking zien we de zogenaamde delta-functie. Deze functie is altijd nul, behalve als m en n hetzelfde zijn. In dat geval is de delta-functie gelijk aan 1. De bovenstaande formule blijkt niet alleen te gelden voor het deeltje in het doosje, maar voor alle situaties. Als een functie aan deze eigenschap voldoet, dan spreken we van orthonormaliteit. De verschillende ψ die mogelijk zijn gedragen zich een beetje als eenheidsvectoren die loodrecht op elkaar staan. Als je twee dezelfde eenheidsvectoren met elkaar vermenigvuldigd dan krijg je 1 en als je twee verschileende met elkaar vermenigvuldigd, dan krijg je 0. Zoals we later in dit hoofdstuk zullen zien wordt het daarom handig om de oplossingen ψ te zien als vectoren.
Een deeltje in een één dimensionaal doosje zal een staande golf vormen. In het eerste deel van deze paragraaf zullen we laten zien dat we voor staande golven de golffunctie kunnen schrijven als een functie ψ afhankelijk van x keer een functie φ afhankelijk van t. Oftewel:
$$ \Psi = \psi(x) \phi(t) $$De Schrodingervergelijking wordt in dit geval:
$$ i\hbar \frac{d\Psi}{dt} = - \frac{\hbar^2}{2m} \frac{d^2\Psi}{dx^2} + E_{pot}\Psi$$ $$ i\hbar \psi \frac{d\phi}{dt} = - \frac{\hbar^2}{2m} \phi \frac{d^2\psi}{dx^2} + E_{pot}\phi\psi$$Dit kunnen we herschrijven tot:
$$ i\hbar \frac{1}{\phi} \frac{d\phi}{dt} = - \frac{\hbar^2}{2m} \frac{1}{\psi} \frac{d^2\psi}{dx^2} + E_{pot} $$De linkerkant van de vergelijking is nu afhankelijk van t en rechterkant van x. Als we een golfje op twee verschillende tijden t op dezelfde plaats x zetten, dan blijft de rechterkant van deze vergelijking dus gelijk. Dit betekent dat de linkerkant ook gelijk moet blijven en dat de linkerkant dus onafhankelijk is van de tijd. De linkerkant is dus onafhankelijk van zowel plaats als tijd. Anders gezegd - de linkerkant van de vergelijking is constant. Als gevolg moet de rechterkant dan ook constant zijn. We noemen deze constante C. Als we de rechterkant gelijkstellen aan deze constante, dan vinden we:
$$ - \frac{\hbar^2}{2m} \frac{1}{\psi} \frac{d^2\psi}{dx^2} + E_{pot} = C $$Dit kunnen we herschrijven tot:
$$ - \frac{\hbar^2}{2m} \frac{d^2\psi}{dx^2} + E_{pot}\psi = C\psi $$ $$ \hat{E}\psi = C\psi $$De constante C blijkt gelijk te zijn aan de energie. Dit kunnen we laten zien door de gemiddelde energie van de golf uit te rekenen:
$$ \langle E \rangle = \int \psi^* \hat{E} \psi dx = C \int \psi^* \psi dx = C $$In de laatste stap hebben we gebruikt dat de integraal van de kans over de hele ruimte gelijk is aan 1. Er is immers altijd 100% kans dat het deeltje ergens in de volledige ruimte zit. De formule wordt dus:
$$ - \frac{\hbar^2}{2m} \frac{d^2\psi}{dx^2} + E_{pot}\psi = E\psi $$Dit wordt ook wel de tijdsonafhankelijke Schrödingervergelijking genoemd.
Het linkerdeel wordt met dezelfde constante:
$$ i\hbar \frac{1}{\phi} \frac{d\phi}{dt} = E $$Dit kunnen we herschrijven tot:
$$ i\hbar \frac{d\phi}{dt} = E \phi $$Deze formule heeft de volgende oplossing:
$$ \phi = e^{-iEt/\hbar} $$De volledige oplossing bij het scheiden van variabelen wordt dus:
$$ \Psi = \psi (x) e^{-iEt/\hbar} $$De kans wordt in dat geval:
$$ \Psi^* \Psi = \psi^* e^{iEt/\hbar} \psi e^{-iEt/\hbar} = \psi^* \psi $$In de laatste stap hebben gebruikt dat de twee e-machten samen e0 worden en dit is gelijk aan 1. Omdat ψ alleen afhankelijk is van x en niet van t, hebben we hier gevonden dat de kansverdeling van deze oplossing constant blijft in de tijd. Dit is precies wat we verwachten bij een staande golven.
We hadden de waarde van A ook nog even kunnen bepalen. Dit doen we als volgt. Als we de kans integreren van 0 tot L, dan moeten we 1 vinden. Er geldt dan dus:
$$ \int^{L}_{0} \psi^*\psi dx = \int^{L}_{0} A \sin{^2\frac{n\pi x}{L}} dx = 1 $$Deze vergelijking blijkt alleen te kloppen als:
$$ A = \sqrt{\frac{2}{L}} $$De golffunctie in de doos wordt dus:
$$ \psi = \sqrt{\frac{2}{L}} \sin{\frac{n\pi x}{L}} \;\;\;\; n=1,2,3,... $$De bijbehorende kansverdeling wordt:
$$ P = \psi^*\psi = \frac{2}{L}\sin{^2\frac{n\pi x}{L}} $$We bestuderen nu een vrij deeltje. Dit is een deeltje met alleen kinetische energie. De tijdsonafhankelijke Schrödingervergelijking wordt in dat geval:
$$ -\frac{\hbar^2}{2m} \frac{d^2\psi}{dx^2} = E\psi $$De genormaliseerde oplossing van deze vergelijking voor een specifieke p is gelijk aan:
$$ \psi_p(x) = \frac{1}{\sqrt{2\pi \hbar}}e^{ipx/\hbar} $$Als we de kans over de hele ruimte bepalen voor een specifieke p, dan vinden we:
$$ \int_{-\infty}^\infty \psi_p^*\psi_p dx = \frac{1}{2\pi \hbar} \int_{-\infty}^\infty dx = \infty $$In de tweede stap zijn de twee e-machten tegen elkaar weggevallen. De kans wordt echter geen 1, maar oneindig. We zeggen hier ook wel dat de deze golffunctie niet normalizeerbaar is. Hieruit kunnen we concluderen dat een vrij deeltje met een specifieke golflengte geen valide fysische oplossing is. Er bestaat dus niet een deeltje met een specifieke impuls en een specifieke golflengte.
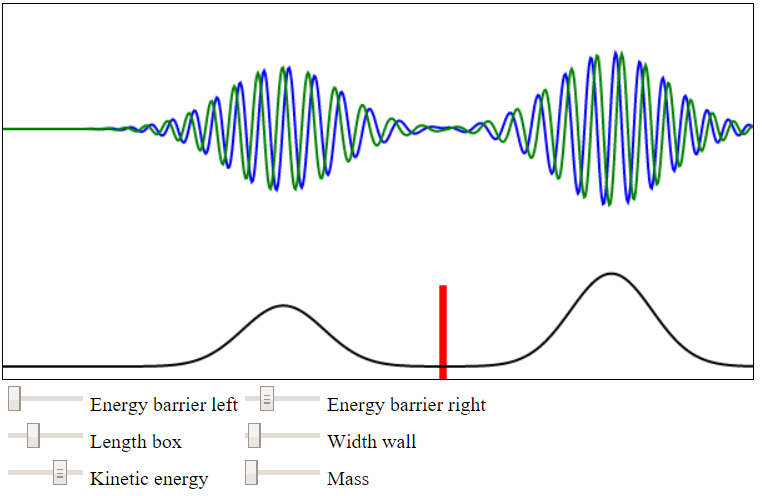
Het blijkt wel mogelijk te zijn om een normalizeerbare oplossing te vinden als we een superpositie nemen van hele set aan golffuncties met verschillende p. We kunnen ons dit als volgt voorstellen. In de onderstaande animatie zien we als de schuifknop naar links is geschoven een golf met één vaste golflengte. Zoals je ziet neemt de amplitude van deze golf niet af met afstand. Deze golf zou zich moeten verspreiden over het hele universum. Het is daarom niet gek dat deze golf niet normalizeerbaar is. Als we de schuifknop naar rechts schuiven, dan wordt een superpositie te zien van verschillende golven met verschillende golflengte. Als we vele golven bij elkaar optellen, dan zie je dat het mogelijk is om een gelocalizeerde golf te krijgen. Deze golf is wel normalizeerbaar.
Om dit idee uit te werken maken we de oplossing tijdsafhankelijk en nemen we een superpositie voor alle mogelijke golffuncties voor verschillende p:
$$ \Psi(x,t) = \frac{1}{\sqrt{2 \pi \hbar}} \int_{-\infty}^\infty \phi(p) e^{i/\hbar(px- Et)} dp $$φ(p) is hier een constante die anders kan zijn voor elke waarde van p. De term speelt dezelfde rol die cn speelde in de vorige paragraaf. Het is de amplitude die vertelt hoeveel een bepaalde stationary state bijdraagt aan de totale golf.
We schrijven de bovenstaande golf ook beknopter opschrijven als:
$$ \Psi(x,t) = \frac{1}{\sqrt{2 \pi \hbar}} \int_{-\infty}^\infty \Phi(p,t) e^{ipx/\hbar} dp $$We hebben hier gebruikt dat:
$$ \Phi(p,t) =\phi(p) e^{-iEt/\hbar} $$We noemen dit de impuls-golffunctie.
De bovenstaande integraal blijkt om te schrijven in:
$$ \Phi(p,t) = \frac{1}{\sqrt{2 \pi \hbar}} \int_{-\infty}^\infty \Psi(x,t) e^{-ipx/\hbar} dx $$Dit kan je zien door deze vergelijking in de normale golffunctie te stoppen en dan de integratie uit te voeren.
Met deze formule kunnen we uitrekenen hoe een bepaalde golffunctie zich ontwikkeld in de tijd. Dit werkt als volgt. Eerst bestuderen we de bovenstaande formule voor t = 0:
$$ \phi(p) = \frac{1}{\sqrt{2 \pi \hbar}} \int_{-\infty}^\infty \Psi(x,0) e^{-ipx/\hbar} dx $$Als we hier de vorm van de golffunctie op tijdstip t = 0 in invullen, dan vinden we dus φ(p). Hiermee kunnen we de impuls-golffunctie Φ(p,t) uitrekenen en hiermee kunnen we Ψ(x,t) uitrekenen voor een willekeurig tijdstip t.
In de onderstaande animatie is dit probleem numeriek opgelost. In het bovenste deel van de animatie zie je het reëele en het imaginaire deel van de golffunctie. In het onderste deel zie je de kansverdeling.
Merk op dat de golffunctie voor het vrije deeltje zich in de tijd uitspreid over een steeds groter gebied. Dit is te verwachten omdat het golfpakketje bestaat uit een superpositie van allerlei golven met verschillende golflengte en dus met een verschillende impuls en snelheid.
PERIODIEK SWe gaan nu de oplossing bestuderen van de Schrödingervergelijking voor het waterstofatoom. Omdat het elektron in waterstof een staande golf vormt, kunnen we gebruik maken van de tijdsonafhankelijke Schrödingervergelijking. We moeten deze vergelijking wel uitbreiden naar drie dimensies:
$$ E\psi = -\frac{\hbar^2}{2m}(\partial_x^2 + \partial_y^2 + \partial_y^2 )\psi + E_{pot}\psi $$Voor de potentiële energie gebruiken we de elektrische energie:
$$ E_{pot} = -\frac{fe^2}{r} $$De oplossing van voor deze vergelijking is enorm. De formule beslaat drie regels en het heeft daarom weinig zin om deze op dit moment te laten zien. Wat wel belangrijk is om te weten is dat de formule afhankelijk is van drie constanten genaamd n, m en l. De n staat wederom voor het energieniveau en de energie wordt gegeven door de formule die ook Bohr had gevonden in zijn model:
$$E_n = -\frac{1}{n^2}\left(\frac{fe^2}{2 a_B}\right)$$ $$ n = 0,1,2,3... $$De constante l is gerelateerd aan het impulsmoment van het elektron (L). l is een heel getal met een waarde die kan lopen van nul to n-1:
$$ \hat{L}^2 \psi = \hbar^2l(l+1)\psi $$ $$ l=0,1,2,3,...,n-1 $$Merkwaardig is dat l=0 ook toegestaan is. Hier heeft het elektron geen impulsmoment. In newtoniaanse mechanica zou het elektron zonder impulsmoment in de kern storten. In de kwantummechanica is dit blijkbaar mogelijk.
De constante m is gerelateerd aan de z-component van het impulsmoment van het elektron (Lz). m is een heel getal met een waarde die kan lopen -l tot l:
$$ \hat{L}_z \psi = \hbar m \psi $$ $$ m = -l, -l+1, ..., 0, ...,l-1,l$$Voor l = 0, kan m dus alleen de waarde nul aannemen. Voor l = 1 kan m de waarde -1, 0 en 1 aannemen. Voor l = 2 kan m de waarde -2, -1, 0, 1 en 2 aannemen etc.
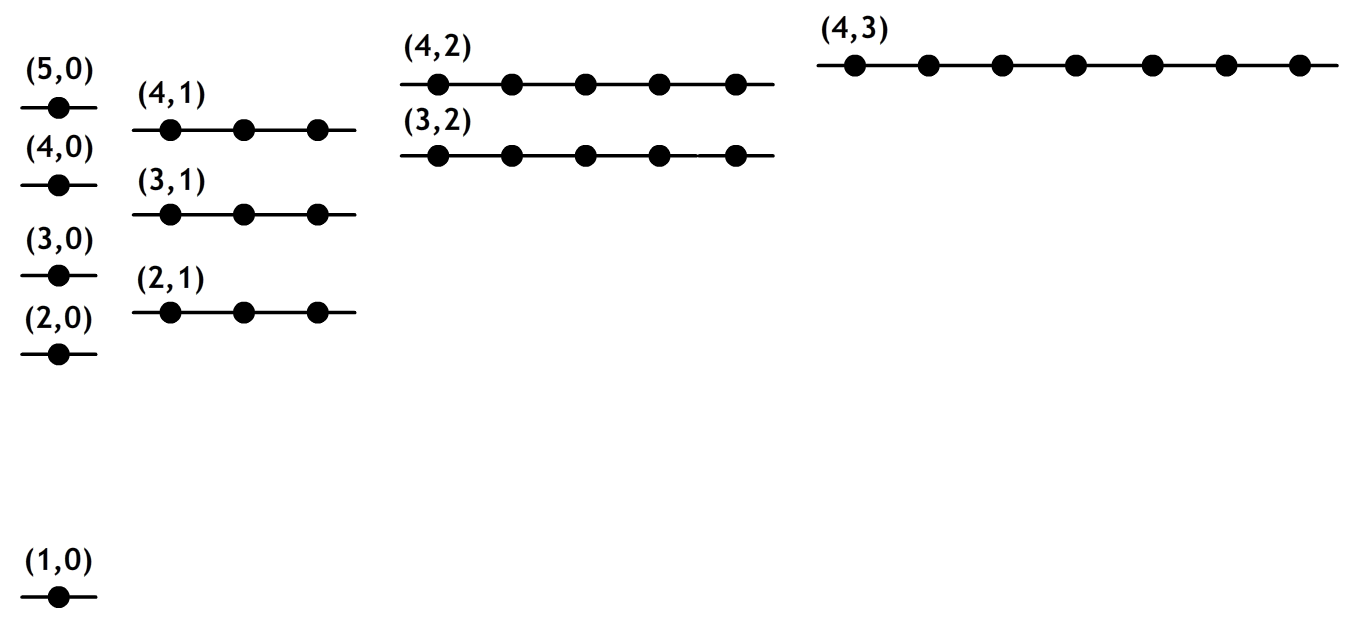
De verschillende mogelijk waarden voor n, l en m zijn hieronder schematisch weergegeven. Op de verticale as vinden we de energielevels n. Op de horizontale as vinden we de l. Het aantal bolletjes bij elke waarde van (n,l) komt overeen met de mogelijke waarden van m. Zoals je kunt zien geldt dat voor elke schil n2 mogelijke combinaties van l en m bestaan.
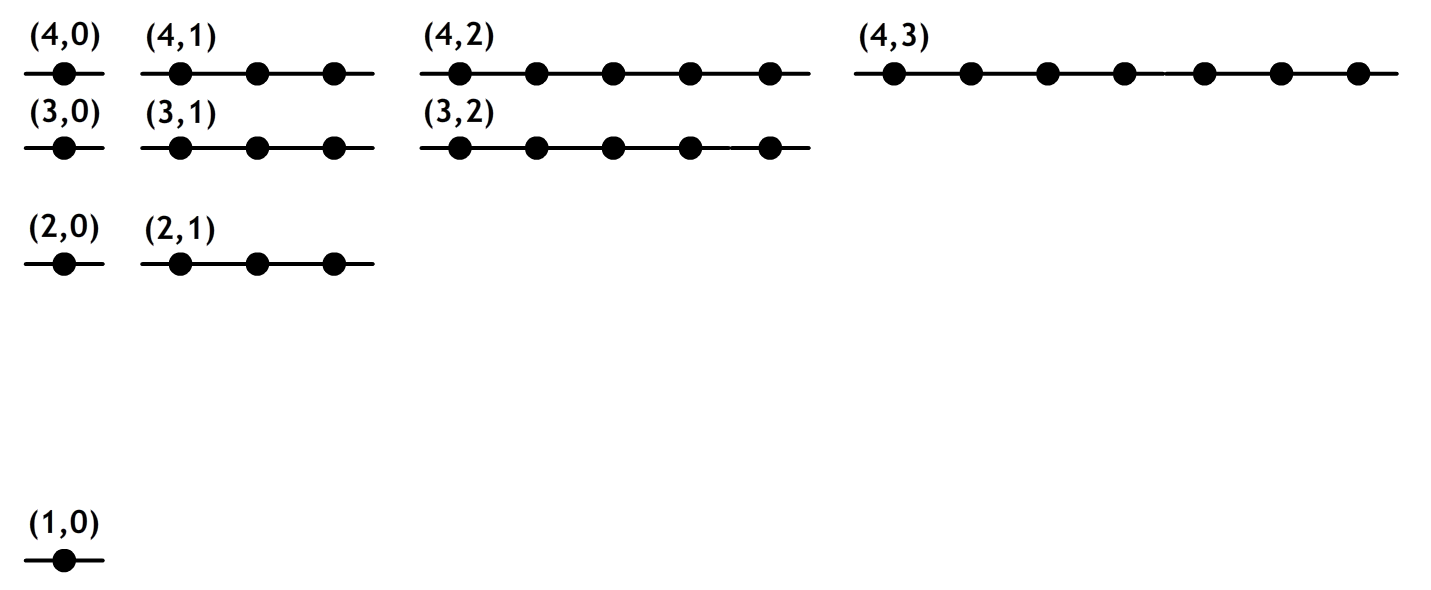
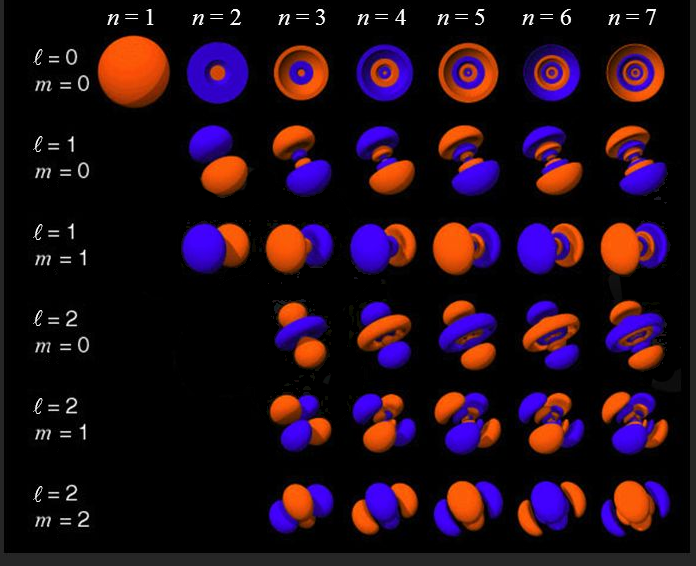
Hoewel we met de Schrödingervergelijking dezelfde formule voor de energie hebben gevonden als Bohr, is het totale plaatje toch een stuk ingewikkelder. Voor verschillende n, l en m is de golffunctie van waterstof hieronder afgebeeld.
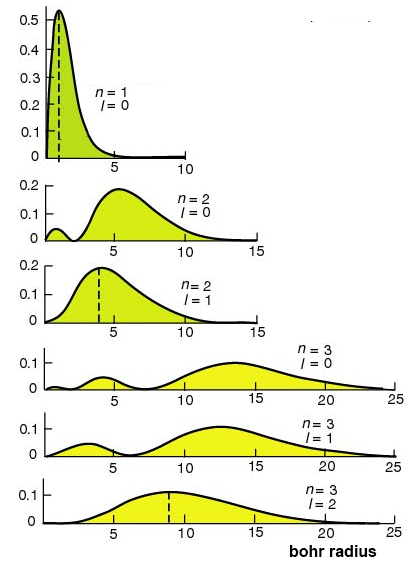
Zelfs met m=0 en l=0 krijgen we niet de nette schillen op specifieke afstanden, zoals Bohr zich dat voorstelde. We krijgen dan een spherisch symmetrische functies met daarin knopen en buiken. Dit kunnen we ons het gemakkelijkst voorstellen met een grafiek waarbij we de kansverdeling weergeven om het elektron op een bepaalde plek aan de te treffen (zie de onderstaande afbeelding). Bij (1,0) zien we een verdeling met een piek die zich precies op de bohrstraal bevindt. Het doet dus denken aan de cirkelbaan met n=1 van het bohratoom, maar het elektron kan zich nu ook rondom deze straal bevinden. Bij (2,0) vinden we een knoop. Een bepaalde straal waar het elektron zich niet kan bevinden. Soms zit het elektron zich aan de ene kant van de knoop en soms aan de andere. Dit doet denken aan een elliptische baan. Bij (2,1) hebben hebben we weer een cirkelbaan en de straal komt hier weer overeen met de straal die Bohr had gevonden bij n = 2. Etc.
Het Periodiek systeem
In de 19de eeuw werd het periodiek systeem der elementen ontdekt. Er werd ontdekt dat als atomen in volgorde van massa werden gezet, dat er dan periodiek in dezelfde volgorde een aantal stoffen voorbij kwamen met bepaalde eigenschappen. Zo bleken de atomen in de linker kolom reactieve metalen. De atomen in de rechterkolom zijn edelgassen. De chemsiche eigenschappen herhalen zich dus. Met de kwantummechanica is de vorm van het periodiek systeem begrepen.
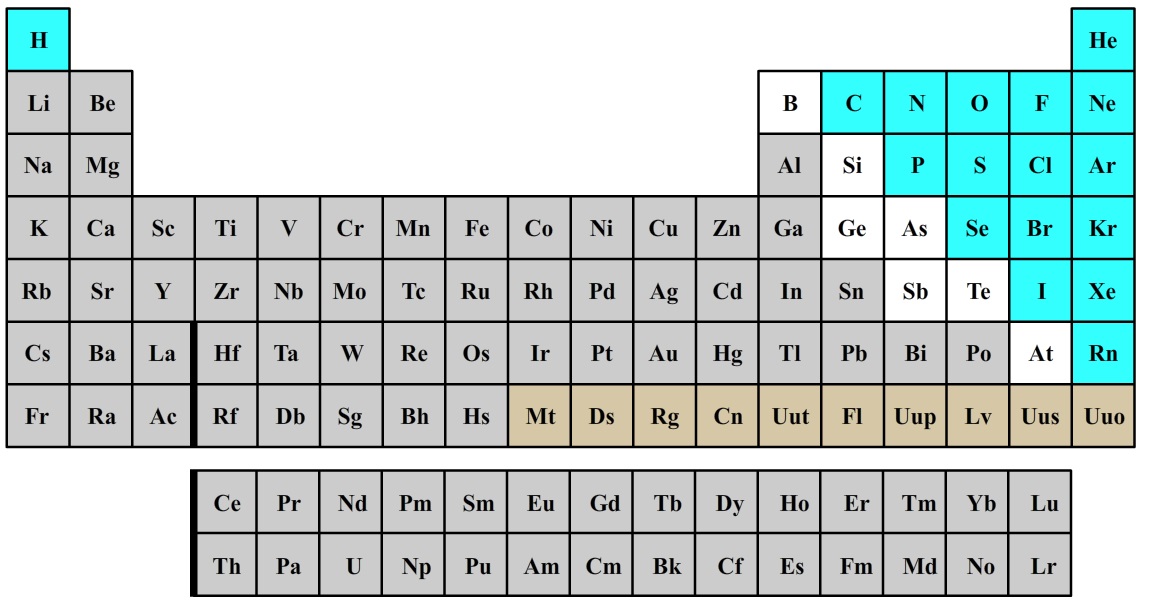
Eerder hebben we gezien dat er voor elk energieniveau n2 mogelijke combinatie van l en m bestaan. Het patroon dat we vinden is dus 1, 4, 9, 16 etc. combinaties. In het periodiek systeem zien we op de rijen 2, 8, 18, 32 elementen. Dit is telkens precies 2x zo veel. Misschien dat deze patronen iets met elkaar te maken hebben.
Pauli loste het verschil van de factor 2 op door aan te nemen dat met elke waarde van n, l en m zich in twee verschillende toestanden konden bevinden. Deze toestanden werden spin-up en spin-down genoemd. Een paar jaar later werd door Stern en Gerlach ontdekt dat dit ook daadwerkelijk het geval was. Als ze waterstofatomen in de grondtoestande (dus met (n,l) = (0,0)) door een nonuniform magneetveld te schoten, bogen sommige deeltjes een beetje naar boven af en andere naar beneden. Dit duidde erop dat zelfs atomen met (0,0) een magneetveld opwerkte. Dit magneetveld ontstond niet door de draaiing van het elektron om de kern, maar door de draaiing van het elektron om zijn eigen as. De kwantumgetallen die horen bij het impulsmoment van het elektron zelf noemen we ls en ms. Om twee opties te krijgen, kiezen we ls = 1/2. Hierbij hoort dan ms = -1/2 en ms = 1/2. Twee opties. Vreemd genoeg hebben we deze opties niet gezien bij het oplossen van de Schrödingervergelijking. Hier konden de kwantumgetallen l alleen maar hele waarden aannemen. Dit probleem lossen we over twee paragrafen op als we naar de relativistische versie van de kwantummechanica gaan kijken.
Tevens nam hij aan de twee elektronen niet indezelfde toestand konden zitten. Dit wordt het uitsluitingsprincipe van Pauli genoemd. Met deze twee aannames lukte het om het periodiek systeem te begrijpen.
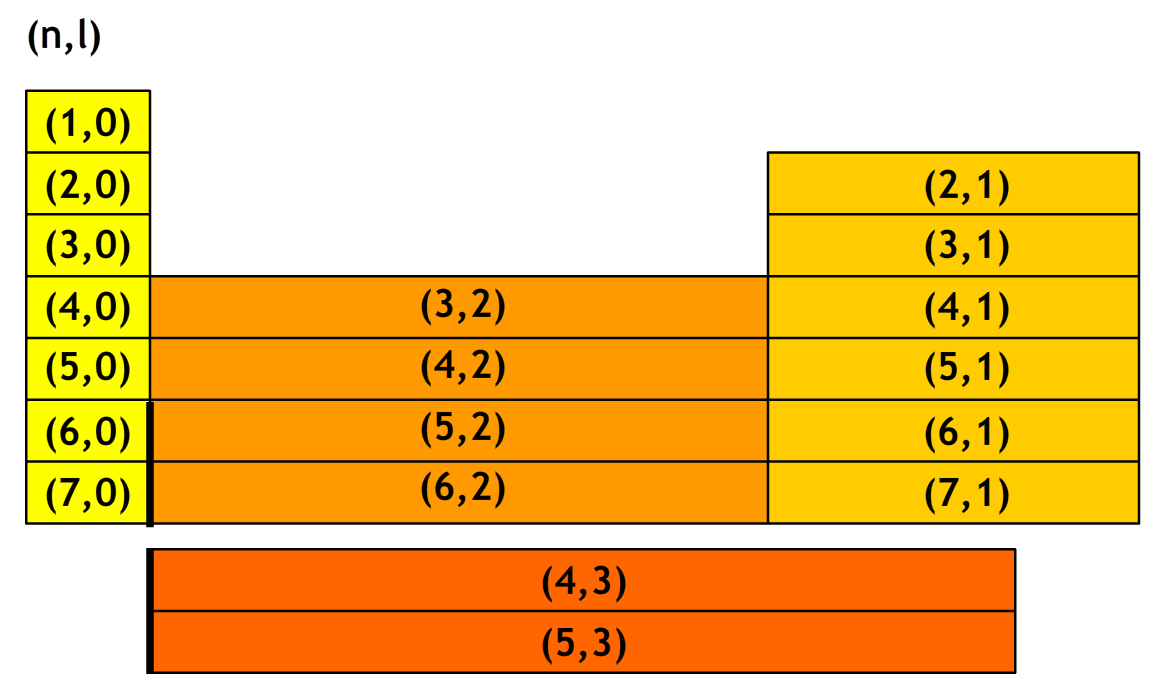
Om te begrijpen hoe dit werkt moeten we eerst begrijpen dat de energieniveaus er bij elementen zwaarder dan waterstof iets chaotischer uitzien. Dit komt omdat deze elementen meerdere atomen bevatten die elkaar ook weer afstoten. Als we hiervoor corrigeren, dan vinden we de volgende energielevels:
Bij waterstof zit er een elektron in de grondtoestand (1,0). Bij helium zit het tweede elektron in de grondtoestand met zijn spin in de andere richting. Dan zijn alle posities in de eerste schil vervult. Dan vult zich eerst (2,0) en dan (2,1). Er passen hier 8 combinaties in, overeenkoment met lithium tot neon. Dan hebben (3,0) en (3,1) de laagste energie. Ook hier passen 8 combinaties in, overeenkoment met natrium tot argon. Daarna heeft niet (3,2) maar (4,0) de laagste energie, daarna (3,2) en daarna (4,1). Dit geeft ons de 18 elementen van kalium tot krypton. Etc.
 Rekenen met de schrödingervergelijking
Rekenen met de schrödingervergelijking
|
|