Extra stof hoofdstuk trillingen
De Golfvergelijking

Stel we bestuderen een klein stukje dx van een lang touw waar transversale golven door lopen. Het linker deel van dit stukje bevindt zich op positie x_b en het rechter deel op positie x_e (zie de onderstaande afbeelding). Op dit kleine stukje touw werken dan twee spankrachten F_s,b en F_s,e.

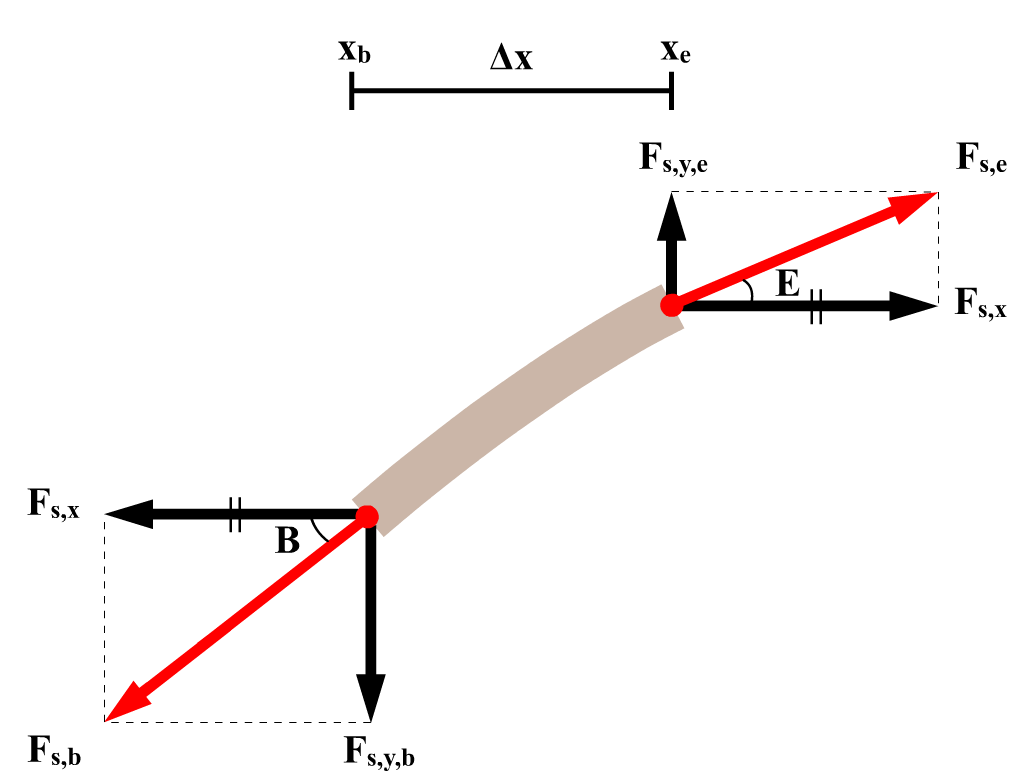
Omdat het touw alleen transversaal trilt, bewegen de deeltjes waar het touw uit bestaat alleen in verticale richting. In horizontale richting staat de deeltjes dus stil, hetgeen betekent dat de horizontale componenten van deze twee spankrachten aan elkaar gelijk moet zijn. Met behulp van de hoeken B en E vinden we dan:

$$ F_{s,x} = F_{s,b} \cos{B} $$ $$ F_{s,x} = F_{s,e} \cos{E} $$

In verticale richting kan wel een resulterende kracht werken. Er geldt dus:

$$ F_{s,y,e} - F_{s,y,b} = F_{res}$$ $$ F_{s,e}\sin{E} - F_{s,b}\sin{B} = ma$$

De versnelling van het lijnstukje in de verticale richting kunnen we ook schrijven als de tweede afgeleide van de uitwijking naar de tijd. De massa van het lijnstukje kunnen we ook schrijven als ρdx. ρ is hier de dichtheid van het lijnstukje (in kilogram per meter). We vinden hiermee:

$$ F_{s,b}\sin{E} - F_{s,b}\sin{B} = \rho dx \frac{\partial^2u}{\partial t^2} $$

Als we beide zijden door F_s,x delen, dan vinden we:

$$ \frac{ F_{s,e}\sin{E}}{ F_{s,x}} - \frac{ F_{s,b}\sin{B}}{ F_{s,x}} = \frac{\rho dx}{F_{s,x}} \frac{\partial^2u}{\partial t^2} $$

Eerder hebben we gevonden dat F_s,x=F_s,bcos(B) en F_s,x=F_s,ecos(E), kunnen we dit herschrijven tot:

$$ \frac{ F_{s,e}\sin{E}}{ F_{s,e} \cos{E}} - \frac{ F_{s,b}\sin{B}}{ F_{s,b} \cos{B}} = \frac{\rho dx}{F_{s,x}} \frac{\partial^2u}{\partial t^2} $$

Met de regel sin(α)/cos(α) = tan(α) vinden we:

$$ \tan{E} - \tan{B} = \frac{\rho dx}{F_{s,x}} \frac{\partial^2u}{\partial t^2} $$

Als we nogmaals naar de bovenstaande afbeelding kijken, dan zien we dat de tangens (overstaande gedeeld door aanliggende) op het begin- en eindpunt gelijk is aan:

$$ \tan{E} = \frac{du_e}{dx_e} $$ $$ \tan{B} = \frac{du_b}{dx_b} $$

We vinden hiermee:

$$ \frac{du_e}{dx_e} - \frac{du_b}{dx_b} = \frac{\rho dx}{F_{s,x}} \frac{\partial^2u}{\partial t^2} $$

Aan de linkerkant doen we de afgeleide van de uitwijking aan het eind min de uitwijking aan het begin. We hebben in eerdere hoofdstukken gezien dat een eindwaarde min een beginwaarde ook te schrijven is met een delta-teken. Als we kijken naar een oneindig klein lijnstukje, dan wordt dit een "d". We kunnen de linkerkant dus schrijven als:

$$ d\left( \frac{du}{dx} \right) = \frac{\rho dx}{F_{s,x}} \frac{\partial^2u}{\partial t^2} $$

Als we nu de "dx" nog even naar de linkerkant halen, dan staat hier:

$$ \frac{d \left( \frac{du}{dx} \right) }{dx} = \frac{\rho}{F_{s,x}} \frac{\partial^2u}{\partial t^2} $$

Aan de linkerkant zien we nu de tweede afgeleide naar de positie staat. Dit wordt dus:

$$ \frac{\partial^2u}{\partial x^2} = \frac{\rho}{F_{s,x}} \frac{\partial^2u}{\partial t^2} $$

Dit wordt de golfvergelijking in 1D genoemd. Elke 1D golf - zoals een golf in een touw - moet aan deze vergelijking voldoen. Andersom kunnen we ook zeggen dat de oplossing van deze vergelijking alle mogelijke golfbewegingen in een touw beschrijft. Bijzonder is dat we met deze vergelijking als we de vorm van een golf op een bepaald moment weten, dat we daarmee kunnen berekenen hoe de golf er in de toekomst uit zal zien. We kunnen dan dus een animatie maken van hoe de golf zich zal ontwikkelen. In de onderstaande animatie zien we een simpel voorbeeld:

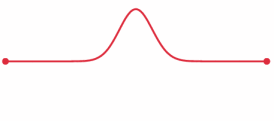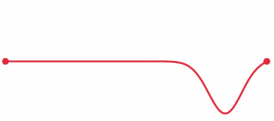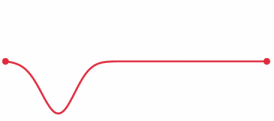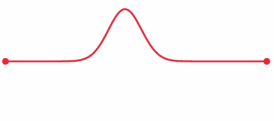
We kunnen de vergelijking nog iets simpelere opschrijven. Hiervoor bestuderen we een oplossing van de vergelijking:

$$ u(x,t) = \sin{\left( x - \sqrt{\frac{F_{s,x}}{\rho}} t \right)} $$

In de opdrachten zal je aantonen dat dit inderdaad een oplossing is van de golfvergelijking.

Als we deze sinus voor verschillende tijdstippen plotten, dan kan je zien dat de term √(F/ρ) gelijk is aan de snelheid. Er geldt dus:

$$ v = \sqrt{\frac{F_{s,x}}{\rho}} $$

Dit kunnen we herschrijven tot:

$$ \frac{1}{v^2} = \frac{\rho}{F_{s,x}} $$

We kunnen hiermee de golfvergelijking schrijven als:

$$ \frac{\partial^2u}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2u}{\partial t^2} $$

We kunnen een soortgelijke afleiding ook doen voor een 2D golf. Een voorbeeld hiervan is een golvend wateroppervlak of de golven die ontstaan in het bekken van een drumstel. De 2D versie wordt:

$$ \frac{\partial^2u}{\partial x^2} + \frac{\partial^2u}{\partial y^2} = \frac{1}{v^2} \frac{\partial^2u}{\partial t^2} $$

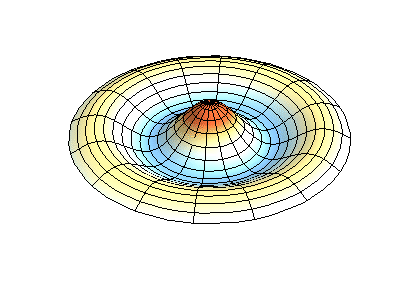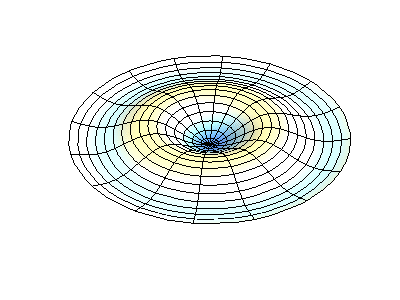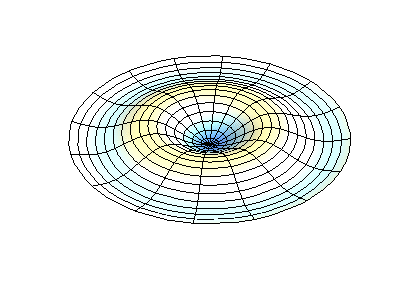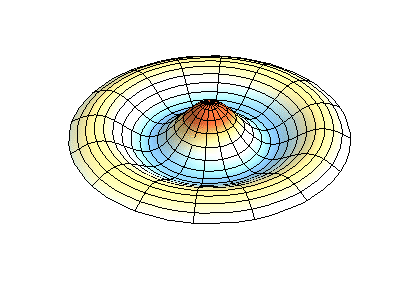
Een 3D versie wordt:

$$ \frac{\partial^2u}{\partial x^2} + \frac{\partial^2u}{\partial y^2} + \frac{\partial^2u}{\partial z^2} = \frac{1}{v^2} \frac{\partial^2u}{\partial t^2} $$

Voorbeelden van een 3D golven zijn geluidsgolven en elektromagnetische golven (licht).

Oplossen van de golfvergelijking

Laat zien dat de volgende formule een oplossing is van de golfvergelijking: $$ u(x,t) = \sin{\left( x - \sqrt{\frac{F_s}{\rho}} t \right)} $$

Laat zien dat deze oplossing een golf beschrijft die naar rechts beweegt.

Nu gaan we een oplossing vinden voor trillingen in een snaar die vastzit op de punten x = 0 en x = L. Voor het oplossen van de golfvergelijking maken we eerst een aanname. Pas later in de opdracht gaan we zien of deze aanname terecht is. We gaan ervan uit dat de uitwijking te schrijven is als: $$ u(x,t) = X(x)T(t) $$ Hier is X een nog onbekende functie die afhankelijk is van x en T een functie die afhankelijk is van t. Laat zien dat in dit geval geldt dat: $$ \frac{1}{T(t)} \frac{d^2T(t)}{dt^2} = v^2\frac{1}{X(x)}\frac{d^2X(x)}{dx^2} $$

We zien nu dat de linkerkant van de vergelijking alleen afhankelijk is van de tijd (t) en de rechterkant alleen van de positie (x). Omdat x en t niet afhankelijk van elkaar zijn, moeten beide kanten constant zijn (als je x verandert, verandert de t niet persé mee). De enige manier waarbij links en rechts altijd gelijk blijven is als beide kanten constant zijn. Stel we maken de constante gelijk aan -ω² (dit blijkt later in de berekening handig te zijn). Laat hiermee zien dat geldt: $$ \frac{d^2T(t)}{dt^2} = -\omega^2 T $$ $$ \frac{d^2X(x)}{dx^2} = -k^2 X $$ Ga er bij de laatste formule vanuit dat ω=kv.

Laat zien dat dit oplossingen zijn van deze vergelijkingen: $$ T = C\sin(\omega t) + D\cos(\omega t) $$ $$ X = A\sin(kx) + B\cos(kx) $$ A, B, C en D zijn hier constanten.

Nu gaan we deze oplossing versimpelen doordat voor de snaar geldt dat: $$ u(0,t) = 0 $$ $$ u(L,t) = 0 $$ Leg uit waaorm dit geldt.

Laat hiermee zien dat: $$ B = 0 $$ $$ A\sin(kL) = 0 $$

Leg uit dat we uit de laatste formule kunnen afleiden dat: $$ k = \frac{n\pi}{L} $$ n is hier een heel getal.

De totale oplossing is nu: $$ u(x,t) = \sin(kx)(AC \sin(\omega t) + AD\cos(\omega t)) $$ Als we kiezen dat AC = E en AD = F, dan vinden we: $$ u(x,t) = \sin(kx)(E\sin(\omega t) + F\cos(\omega t)) $$ Stel dat we de snaar vanuit stilstand loslaten vanuit een bepaalde positie. In dat geval geldt: $$ \frac{du(x,t)}{dt} = 0 \;\;\;\;\text{op t = 0} $$ Leg uit waarom dit geldt.

Laat zien dat we hiermee vinden dat: $$ E = 0 $$ We vinden dat als oplossing: $$ u(x,t) = F \sin(kx) \cos(\omega t) $$

Met k = nπ/L vinden we: $$ u(x,t) = F \sin \left( \frac{n\pi}{L}x \right) \cos \left( \frac{n\pi}{L} vt \right) $$ Laat zien dat voor n = 1 we een snaar vinden die in zijn grondtoon trilt en voor n = 2 een snaar die in zijn eerste boventoon trilt. Kies hiervoor willekeurige waarden voor v en F.

Extra stof hoofdstuk trillingen De Golfvergelijking

Extra stof hoofdstuk trillingen
De Golfvergelijking