Hoofdstuk 9
Kracht
§1 Soorten kracht §2 De Zwaartekracht §3 De krachtenschaal §4 De netto kracht
§1 Soorten kracht
In dit hoofdstuk gaan we leren over krachten. We beginnen deze paragraaf met het introduceren van de verschillende soorten krachten.
We spreken van een kracht (F) als er aan een voorwerp geduwd of getrokken wordt. De bekendste eenheid van kracht is de newton (N). In de natuurkunde geven we krachten symbolisch weer met behulp van zogenaamde vectorpijlen. De pijl start op de plek waar de kracht wordt uitgeoefend. Dit wordt ook wel het aangrijpingspunt genoemd. De pijl wijst in de richting waarin de kracht werkt en de lengte van deze pijl geeft de grootte van de kracht aan. Hoe langer de pijl, hoe groter de kracht.
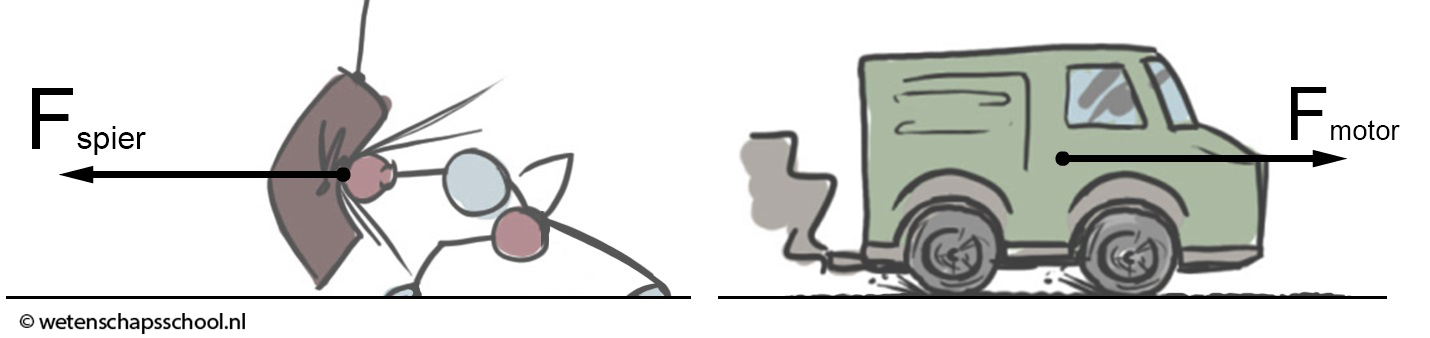
Er bestaan verschillende soorten krachten. Hieronder zien we bijvoorbeeld de spierkracht (Fspier) en de motorkracht (Fmotor) afgebeeld.
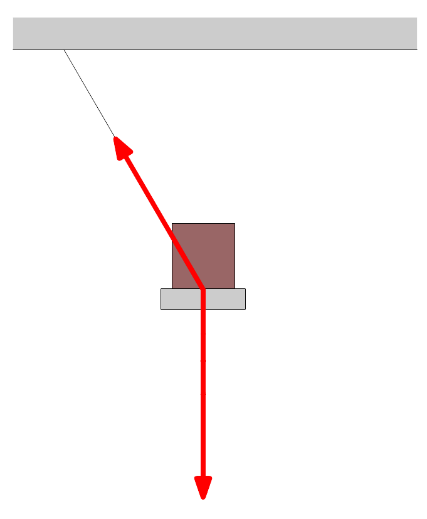
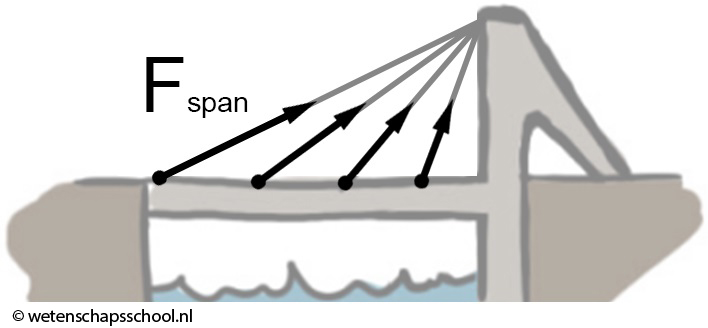
Hieronder is de spankracht (Fspan) afgebeeld. Dit is de kracht waarmee een koord of kabel aan een voorwerp trekt. In het onderstaande voorbeeld zorgen spankrachten in kabels ervoor dat een brug omhooggehouden wordt.
Hieronder is de veerkracht (Fveer) weergegeven. Als je een veer uitrekt of induwt, dan voel je dat de veer weer terug wil naar zijn neutrale vorm. We noemen dit ook wel de evenwichtsstand van de veer. Als we de veer uitrekken, dan wil de veer terug naar binnen. Als we de veer indrukken, dan wil de veer terug naar buiten.

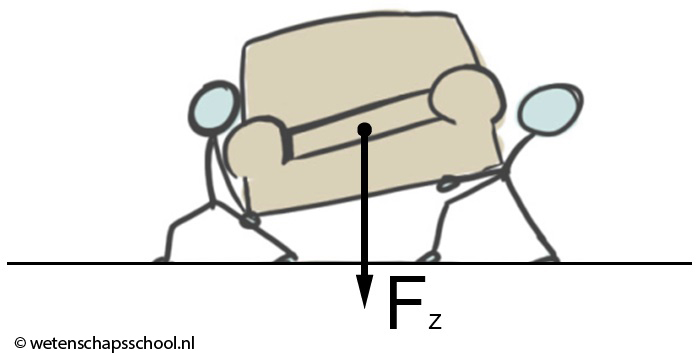
Hieronder is de zwaartekracht (Fz) afgebeeld. De zwaartekracht zorgt ervoor dat voorwerpen richting het centrum van de aarde worden getrokken. Omdat het centrum van de aarde zich recht onder ons bevindt, werkt de zwaartekracht dus altijd recht naar beneden.
De normaalkracht (FN) is de kracht die ervoor zorgt dat een voorwerp niet door een ondergrond heen zakt. Hieronder zien we bijvoorbeeld twee blokken die niet door de grond zakken en een persoon die niet door een boom heen kan duwen. Zoals je kunt zien wijst de normaalkracht in alle gevallen loodrecht op de ondergrond.
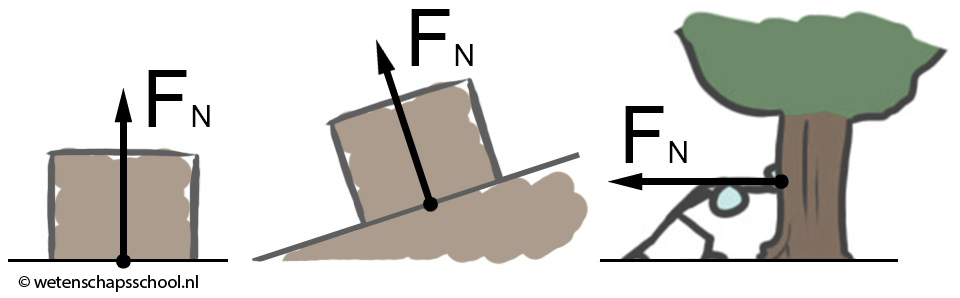
De normaalkracht ontstaat wanneer de atomen in de ondergrond dichter op elkaar worden geduwd. Als atomen echter te dicht op elkaar zitten, dan stoten ze elkaar af. Deze afstotende kracht is de normaalkracht.
Een ander voorbeeld is de wrijvingskracht (Fw). Er bestaan verschillende soorten wrijvingskracht. In de onderstaande afbeelding wordt de schuifwrijvingskracht (Fw,schuif) afgebeeld. Deze kracht ontstaat als we een voorwerp over een ondergrond schuiven. De atomen aan de grond trekken aan de atomen in het voorwerp en dit zorgt voor een afremmende kracht. De schuifwrijvingskracht wijst altijd tegen de bewegingsrichting van het voorwerp in.
Naast de schuifwrijvingskracht bestaat ook nog de rolwrijvingskracht (Fw,rol) en de luchtwrijvingskracht (Fw,lucht). Ook deze krachten werken altijd tegen de bewegingsrichting in.
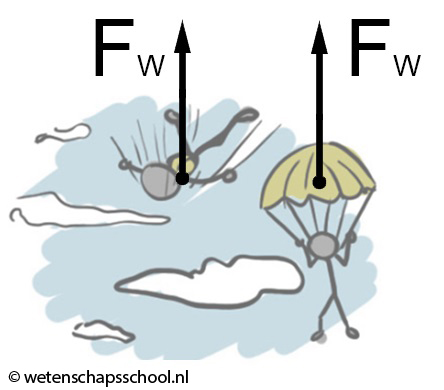
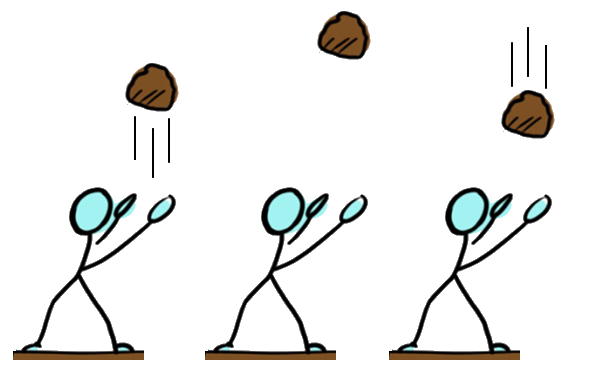
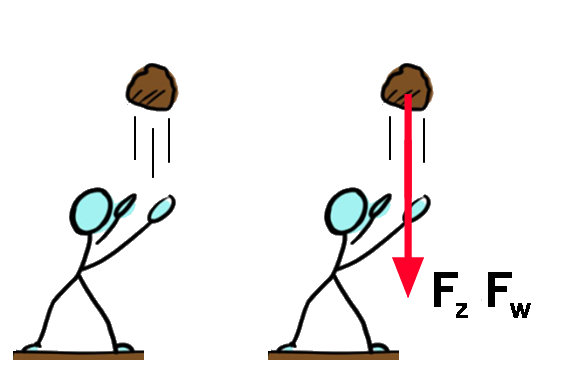
Let erop dat er in sommige gevallen geen kracht in de bewegingsrichting werkt. Neem bijvoorbeeld de onderstaande steen die omhoog gegooid wordt. Deze steen beweegt omhoog, terwijl de krachten op het voorwerp (de zwaartekracht en de wrijvingskracht) juist naar beneden werken. De reden dat de steen toch omhoog beweegt is dat de persoon op een eerder moment een spierkracht omhoog heeft uitgeoefend, maar op het moment dat de steen loskomt van de hand werkt deze spierkracht niet meer. Uiteindelijk zal de zwaartekracht er wel voor zorgen dat de steen afremt en daarna naar beneden zal vallen.
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§2 De zwaartekracht
In deze paragraaf gaan we de grootte van de zwaartekracht berekenen.
De grootte van de zwaartekracht kan berekend worden met de volgende formules:
$$ \text{zwaartekracht} = \text{massa} \times 10 $$
$$ \text{massa} = \frac{\text{zwaartekracht}}{10} $$
|
De massa moet in deze formule altijd gegeven worden in kilogram.
 Voorbeeld
Voorbeeld
|
|
Vraag: Een leerling houdt een steen in zijn handen met een massa van 1800 gram. Bereken de zwaartekracht werkende op de steen. Antwoord: Om de zwaartekracht uit te rekenen, moeten we eerst de massa in kilogram omschrijven: massa = 1800 g = 1,8 kg Nu vullen we de formule in: $$ \text{zwaartekracht} = \text{massa} \times 10 $$ $$ \text{zwaartekracht} = 1,8 \times 10 = 18 \text{ N} $$De zwaartekracht werkende op de steen is dus gelijk aan 18 N.
|
We kunnen de zwaartekracht o.a. meten met een veerunster, ook wel een newtonmeter of krachtmeter genoemd (zie de afbeelding in het volgende voorbeeld). In een veerunster zit een veer. Aan de hand van hoeveel de veer uitrekt, kan de kracht worden afgelezen. Let bij het uitkiezen van een krachtmeter altijd even op het meetbereik. De krachtmeter in de volgende afbeelding meet bijvoorbeeld van 0 tot 50 N. Er zijn ook krachtmeters met een veel kleiner bereik (bijvoorbeeld 0 tot 0,50 N) en ook met een groter bereik (bijvoorbeeld 0 tot 500 N). Hoe groter het bereik, hoe stugger de veer is. Een stugge veer is moeilijk uit te rekken.
Ook geldt dat hoe kleiner het bereik van de veerunster is, hoe nauwkeuriger je de kracht kan aflezen. Het is dus altijd verstandig een veerunster te nemen met een zo klein mogelijk bereik (maar natuurlijk niet zo klein dat je de kracht er niet mee kan meten).
 Voorbeeld
Voorbeeld
|
|
Vraag: Een leerling hangt een blokje aan een krachtmeter. De krachtmeter is hieronder weergegeven:
Bepaal de massa van het blokje. Antwoord: Als we de krachtmeter aflezen, dan vinden we 23 N (ga dit zelf na!): zwaartekracht = 23 N Met de formule voor de zwaartekracht berekenen we nu de massa van het blokje. We kiezen de formule waarmee we de massa kunnen uitrekenen: $$ \text{massa} = \frac{\text{zwaartekracht}}{10} $$ $$ \text{massa} = \frac{23}{10} = 2,3 \text{ kg} $$De massa van het blokje is dus 2,3 kg.
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§3 De krachtenschaal
In deze paragraaf gaan we leren krachten te tekenen op de juiste schaal.
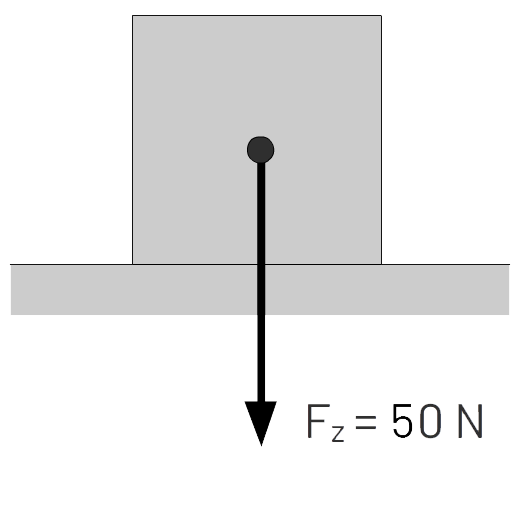
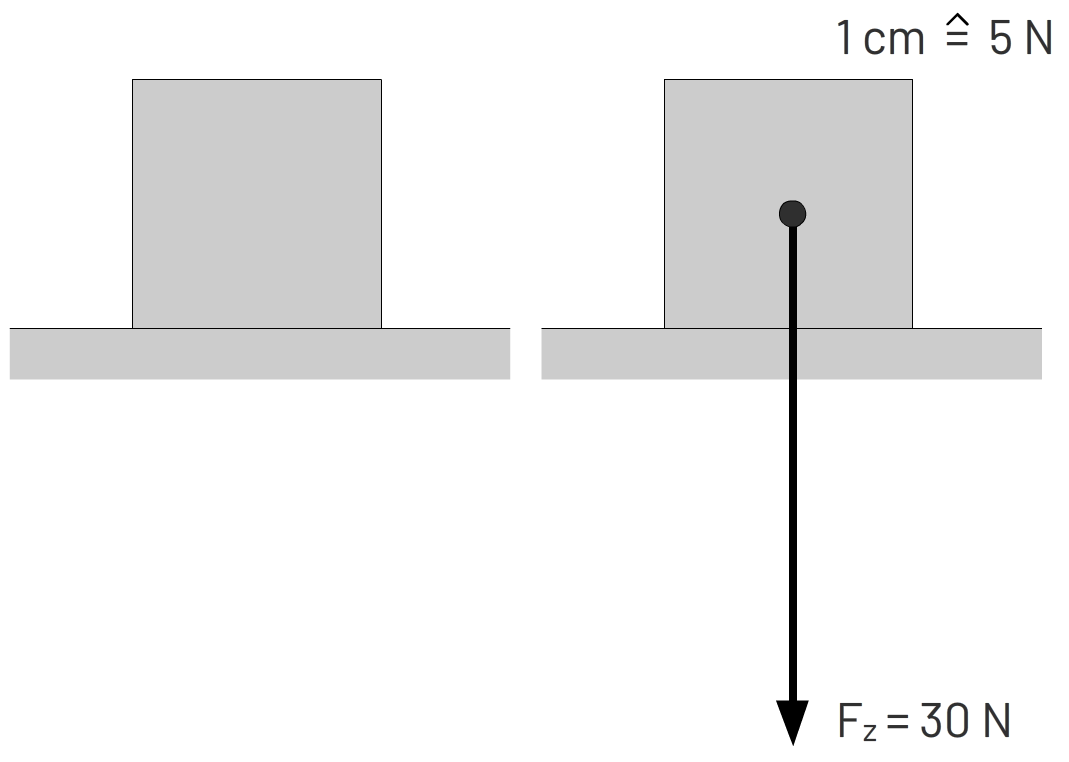
In de rechter afbeelding zien we een blok. Op dit blok werkt een zwaartekracht van 30 N. We kunnen deze kracht met behulp van een vectorpijl weergeven in de tekening. Hiervoor gebruiken we een zogenaamde krachtenschaal. Een voorbeeld van een schaal is:
$$ 1,0 \text{ cm} \;\; \widehat{=} \;\; 5 \text{ N} $$Dit wil zeggen dat elke centimeter van de vectorpijl in de afbeelding overeenkomt met 5 N. Zorg dat je de schaal die je gebruikt altijd noteert. Met een verhoudingstabel kunnen we nagaan hoelang de vectorpijl van de zwaartekracht van 30 N moet zijn:
| 1,0 cm | ... cm |
| 5 N | 30 N |
De gemakkelijkste manier om met verhoudingstabellen te rekenen is door kruislings te vermenigvuldigen. Je vermenigvuldigt in dat geval de twee getallen die diagonaal genoteerd zijn en daarna deel je door het overgebleven getal. In de instructiefilmpjes bij deze paragraaf wordt deze techniek uitgebreid uitgelegd. We vinden hiermee:
| 1,0 cm | 6 cm |
| 5 N | 30 N |
Voor een blok van 30 N hebben we dus een pijl van 6,0 cm nodig. Deze pijl is in de rechter afbeelding getekend.
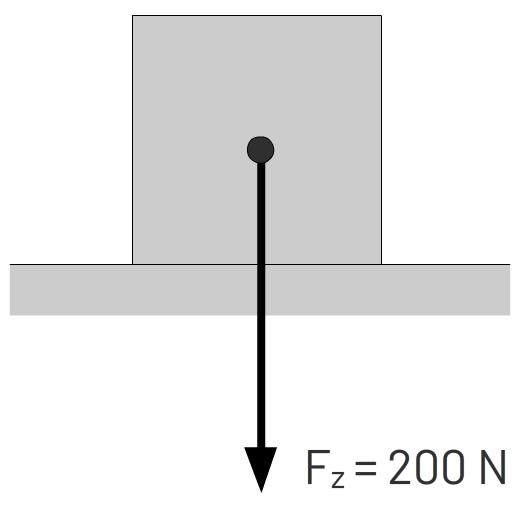
In sommige gevallen is de pijl al gegeven en wordt gevraagd de krachtenschaal te vinden. In de onderstaande afbeelding is de pijl 3,6 cm lang (ga zelf na) en is de kracht gelijk aan 200 N. De schaal bepalen we in dit geval weer met een verhoudingstabel.
| 3,6 cm | 1,0 cm |
| 200 N | 58,8 N |
De krachtenschaal is nu dus:
$$ 1,0 \text{ cm} \;\; \widehat{=} \;\; 58,8 \text{ N} $$
 Voorbeeld
Voorbeeld
| ||||||||
|
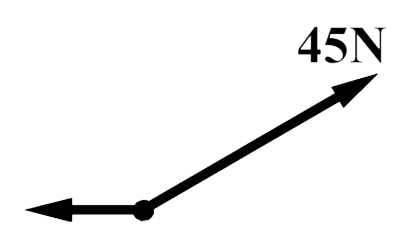
Vraag: In de onderstaande afbeelding zijn twee krachten weergegeven. De rechter kracht heeft een grootte van 45 N. Bepaal de grootte van de linker kracht. Bepaal hiervoor eerst de krachtenschaal.
Antwoord: Als we de rechter kracht (in het boek) opmeten, dan vinden we een lengte van 4,8 cm (meet van het midden van het bolletje tot het puntje van de rechter pijl). Deze kracht heeft een grootte van 45 N. Er geldt dus:
De krachtenschaal is dus: $$ 1,0 \text{ cm} \;\; \widehat{=} \;\; 9,375 \text{ N} $$Met de krachtenschaal kunnen we nu de grootte van de linker kracht vinden. De linker pijl heeft een lengte van 2,1 cm (in het boek!). Hiermee vinden we:
De linker kracht is dus gelijk aan 20 N.
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§4 De netto kracht
In deze paragraaf gaan we krachten bij elkaar optellen. We noemen de totale kracht die op een voorwerp werkt de netto kracht.
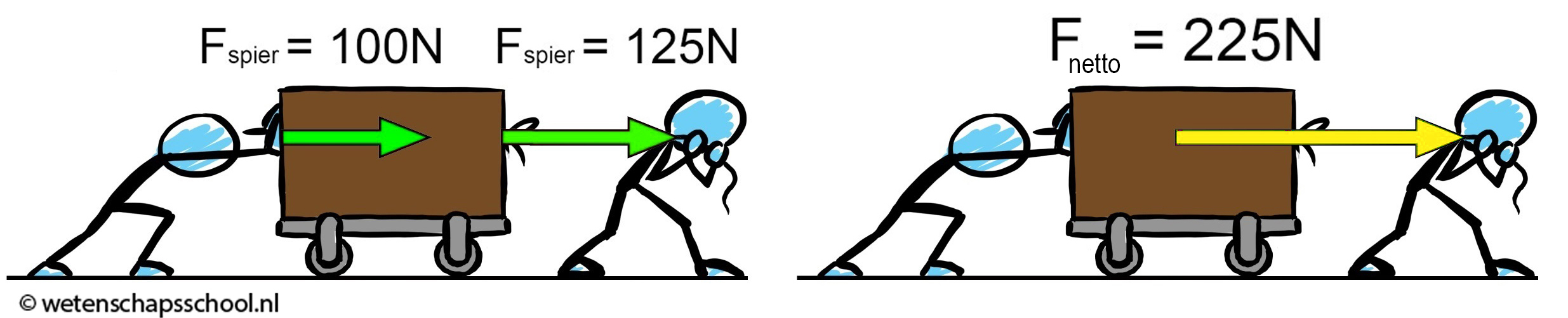
Hieronder zien we twee personen die beide een kracht uit oefenen op een kar. De linker persoon oefent een kracht van 100 N uit en de rechter persoon een kracht van 125 N. In totaal oefenen ze dan een netto kracht naar rechts uit van 100 + 125 = 225 N. Er geldt dus: Fnetto = 225 N.
Hieronder werken twee krachten juist tegen elkaar in. We vinden nu een netto kracht van 40 - 40 = 0 N. Er geldt dus: Fnetto = 0 N.
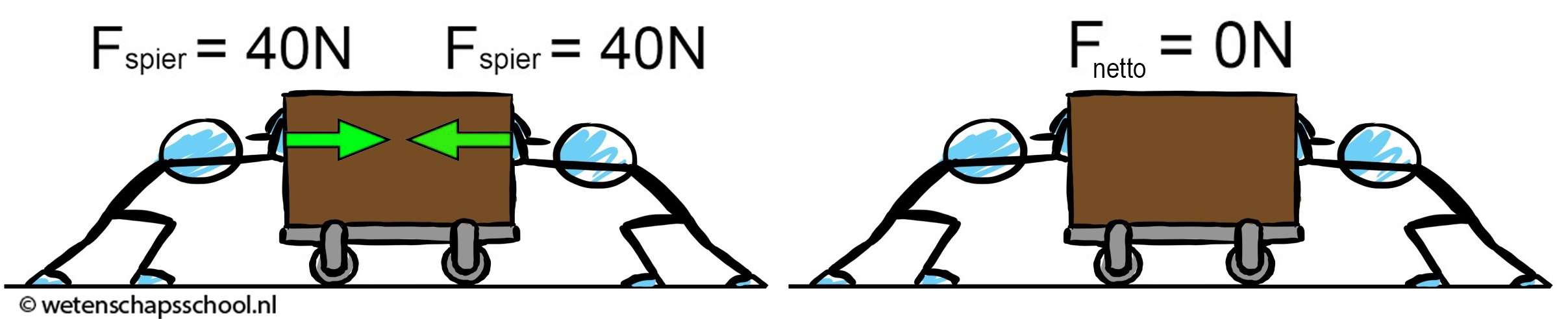
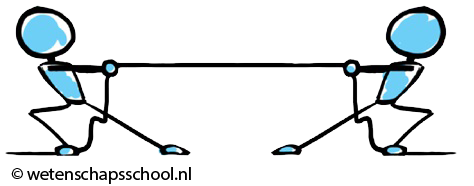
In de onderstaande afbeelding zijn twee leerlingen aan het touwtje trekken. De linker persoon zorgt met zijn voeten voor een wrijvingskracht van 100 N naar links. De rechter persoon zorgt voor een wrijvingskracht van 40 N naar rechts. De linker leerling oefent dus een 100 - 40 = 60 N grotere kracht uit dan de rechter leerling. De netto kracht is dus 60 N en wijst naar links.

Als we ons voortbewegen, zowel te voet als met een voertuig, dan hebben we ook te maken met meerdere krachten. Hieronder zien we bijvoorbeeld een auto die naar rechts rijdt met behulp van de motorkracht. We noemen dit ook wel de aandrijfkracht van de auto. Daarnaast werkt er ook nog een wrijvingskracht tegen de bewegingsrichting in. Deze wrijvingskracht bestaat uit een combinatie van rolwrijving en luchtwrijving.
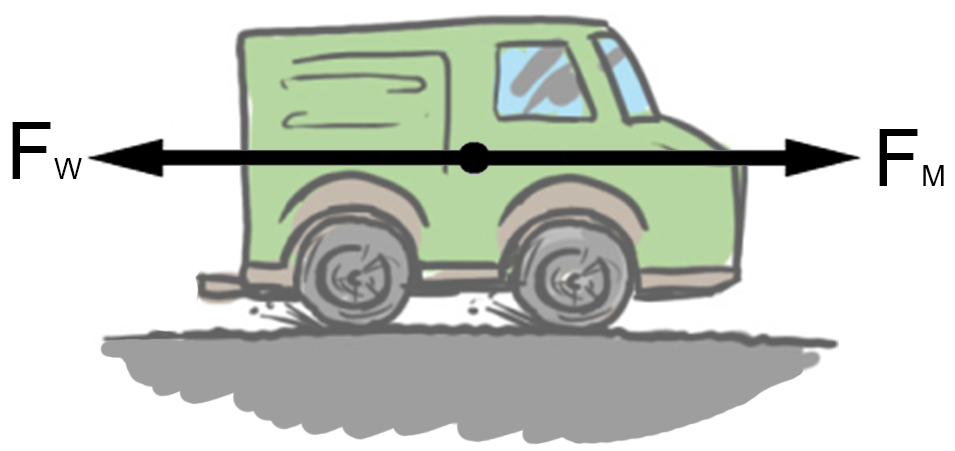
In het bovenstaande voorbeeld zijn de aandrijfkracht en de wrijvingskracht gelijk. De netto kracht is hier dus nul. Dan zou je misschien denken dat het voertuig stil staat, maar dit is niet noodzakelijk het geval. Als de netto kracht nul is, dat staat het voorwerp stil of het voorwerp beweegt met een constante snelheid. Er geldt dus:
| $$ \text{netto kracht is nul} \;\;\; \leftrightarrow \;\;\;\text{stilstand of constante snelheid} $$ |
Als de aandrijfkracht groter is dan de wrijvingskracht, dan versnelt het voertuig. De snelheid neemt dan dus toe.
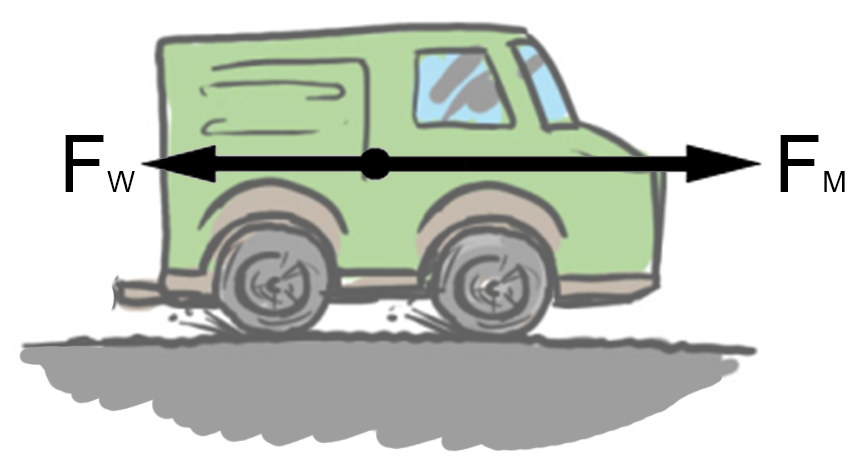
| $$ \text{aandrijfkracht groter dan wrijvingskracht} \;\;\; \leftrightarrow \;\;\; \text{ versnellen} $$ |
Als de aandrijfkracht kleiner is dan de wrijvingskracht, dan vertraagt het voorwerp. De snelheid neemt dan dus af.

| $$ \text{aandrijfkracht kleiner dan wrijvingskracht} \;\;\; \leftrightarrow \;\;\; \text{ vertragen} $$ |
De auto kan ook remmen. In dat geval is er geen aandrijfkracht. De remkracht werkt tegen de bewegingsrichting in:
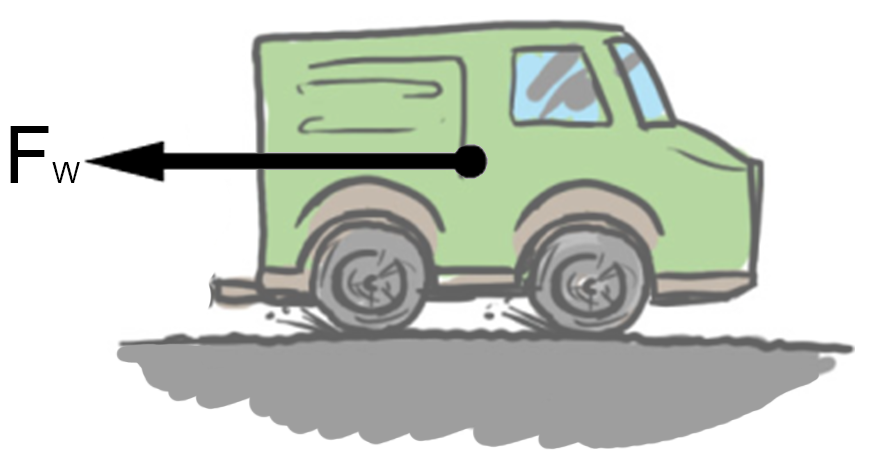
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|