Hoofdstuk 8
Het Systeembord (keuzemodule HAVO)
§1 De EN-poort, de OF-poort en de invertor §2 De comparator §3 De geheugencel §4 De teller
§1 De EN-poort, de OF-poort en de invertor
In dit hoofdstuk gaan we leren werken met het systeembord. Op dit bord zitten een aantal elektrische elementen waarmee we automatische systemen kunnen maken. Het werkt het best als je een systeembord bij de hand hebt tijdens het lezen van dit hoofdstuk, zodat je de theorie meteen kan toepassen. Een online versie kan je hier vinden. In deze paragraaf introduceren we de EN-poort, de OF-poort, de invertor en de pulsengenerator.
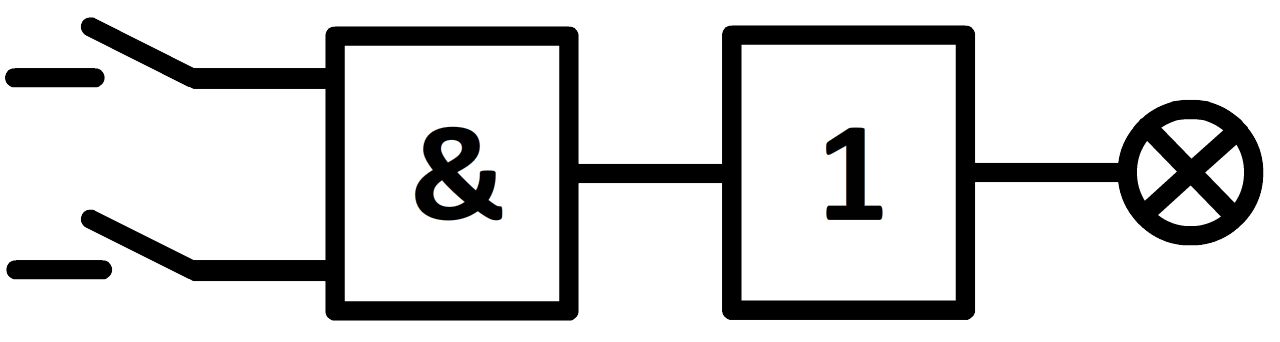
Laten we simpel beginnen. Op het systeembord zijn twee drukknoppen te vinden (zoek ze even op). Sluit deze drukknoppen aan op de twee ingangen van de EN-poort (aangegeven met het "&"-teken) en sluit de uitgang van de EN-poort aan op een LED-lampje (zie de onderstaande afbeelding). We hebben nu een systeem gemaakt waarbij het lampje aangaat wanneer beide knoppen ingedrukt zijn. Merk op dat het lijkt alsof de stroomkring niet gesloten is. Dit is slechts schijn, want met de elektronica onder het systeembord wordt wel degelijk elke stroomkring gesloten.
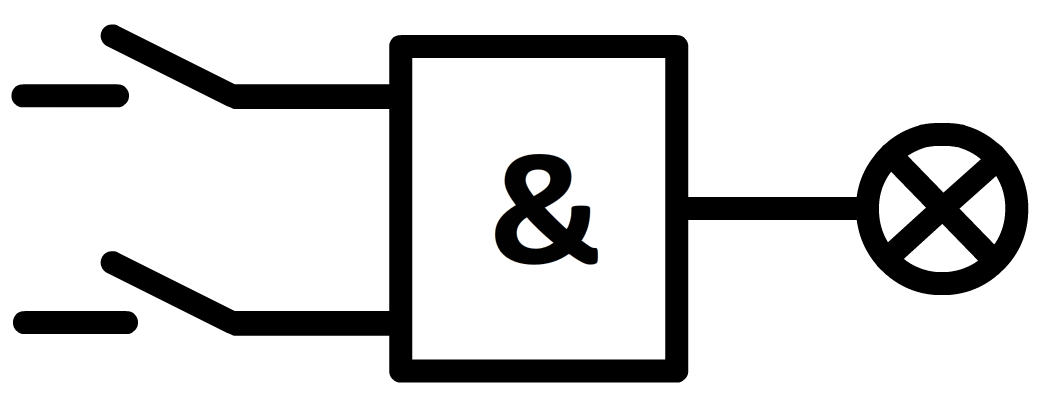
Wat gebeurt er precies bij dit systeem? Als een knop niet is ingedrukt, dan staat er op de uitgang van deze knop een spanning van 0,0 V. Als een knop wel is ingedrukt, dan staat er op de uitgang een spanning van 5,0 V. Omdat er slechts twee opties zijn—0,0 V of 5,0 V—spreken we hier van een binair signaal ("bi" betekent twee). We noemen deze twee opties ook wel "0" en "1". Als op beide ingangen van de EN-poort een "1" staat, dan geeft de uitgang van de EN-poort ook een "1". Deze "1" zorgt er dan voor dat het lampje gaat branden. In de volgende tabel is de werking van een EN-poort samengevat:
| Ingang 1 | Ingang 2 | Uitgang |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Een soortgelijk element is de OF-poort. Als we het onderstaande systeem maken, dan gaat het lampje aan als één of beide knoppen worden ingedrukt.
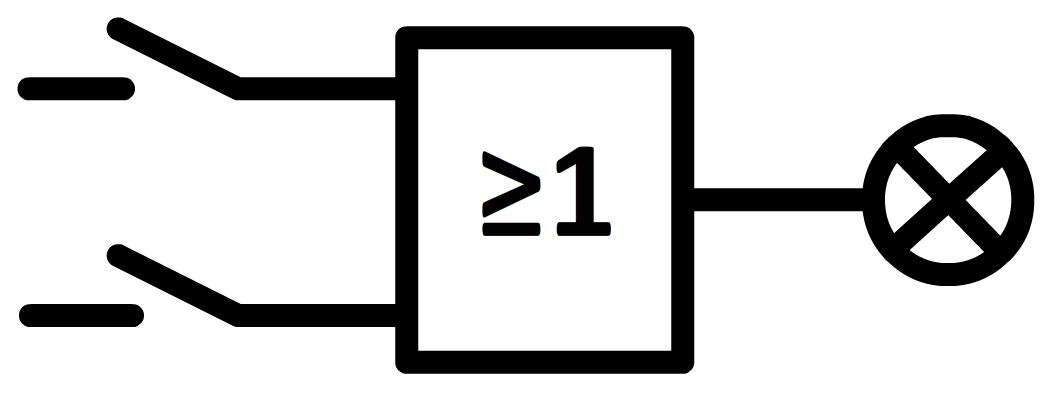
In binaire code kunnen we de werking van de OF-poort als volgt weergeven:
| Ingang 1 | Ingang 2 | Uitgang |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Het onderstaande element noemen we een invertor. De invertor maakt van een "0" op de ingang een "1" op de uitgang en andersom. In dit geval gaat het lampje dus juist aan als de knop niet is ingedrukt en uit als de knop wel is ingedrukt.
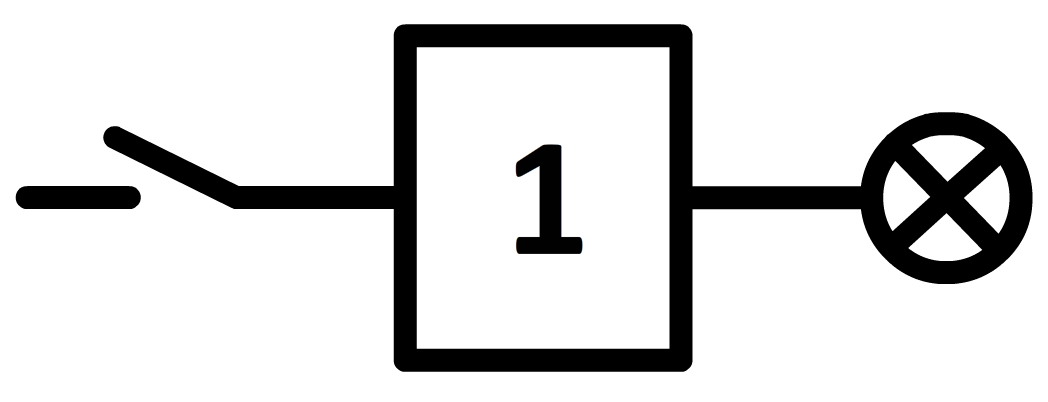
Er geldt dus:
| Ingang | Uitgang |
| 0 | 1 |
| 1 | 0 |
In de onderstaande afbeelding hebben we de pulsgenerator aangesloten op een LED-lamp. De pulsengenerator gaat met een handmatig in te stellen frequentie aan en uit. De frequentie wordt gemeten in hertz (Hz) en dit staat voor het aantal pulsen per seconde. Bij een puls geeft de uitgang van de pulsenteller een "1". Tussen de pulsen in is de waarde "0".
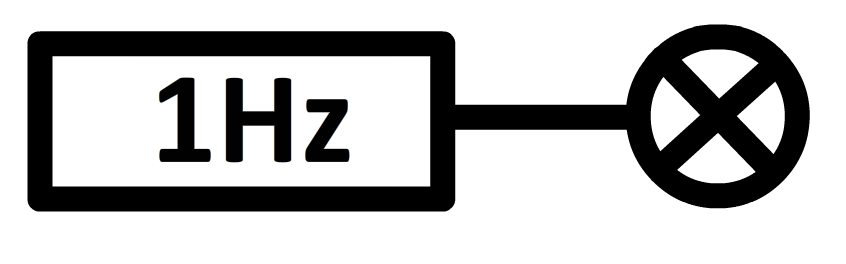
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
| |||||||||||||||
|
§2 De comparator
In deze paragraaf voegen we de comparator toe aan onze systemen. Hiermee gaan we leren om een analoog signaal om te zetten in een digitaal signaal.
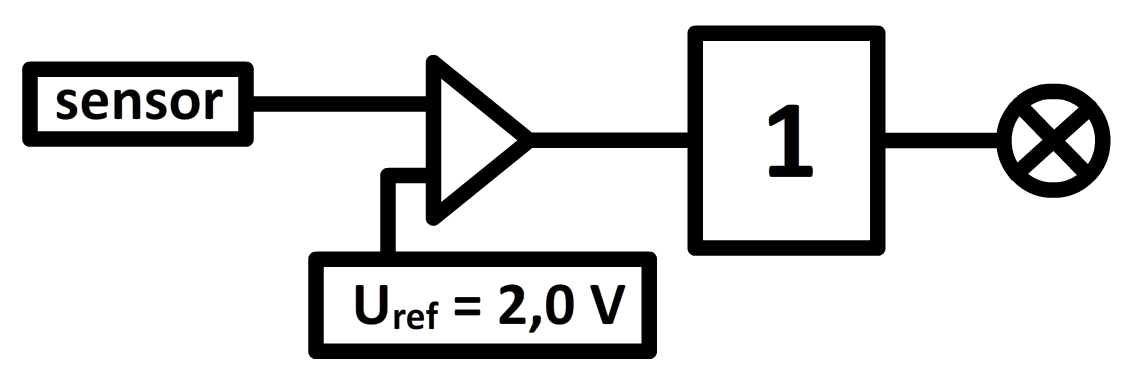
In de onderstaande afbeelding is een zogenaamde comparator weergegeven. Op de ingang van de comparator sluiten we een sensor of een variabele spanning aan. Een sensor is een meetinstrument waarbij de meetwaarde wordt omgezet naar een bepaalde uitgangsspanning. Er bestaan bijvoorbeeld temperatuursensoren, lichtsensoren, geluidsensoren, etc. De uitgangsspanning van een variabele spanning kunnen we zelf met een draaiknop instellen. De comparator kunnen we instellen op een bepaalde referentiespanning. Als de ingangsspanning hoger is dan de referentiespanning, dan geeft de uitgang van de comparator een "1" en anders een "0". In het onderstaande voorbeeld geeft een spanning onder de 2,0 V een "0" en een spanning boven de 2,0 V een "1".
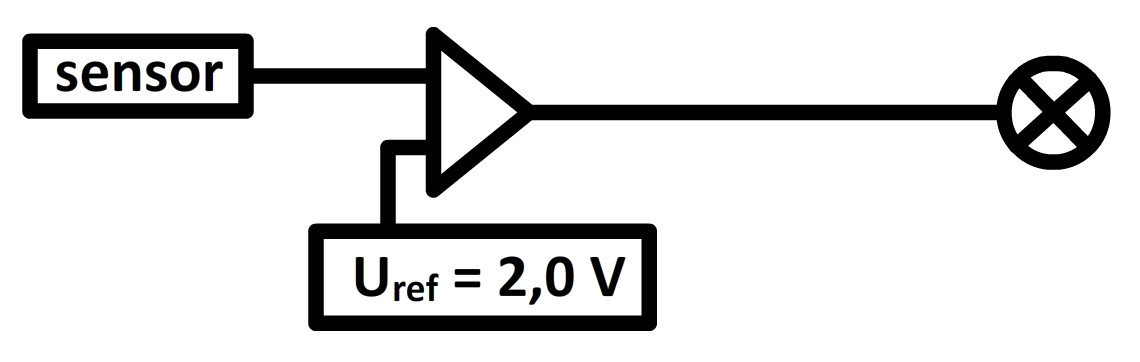
Met een comparator wordt een analoog signaal omgezet in een digitaal signaal. Het analoge signaal kan elke spanning aannemen tussen de 0,0 V en de 5,0 V. Bij een digitaal signaal kan de spanning slechts een eindig aantal specifieke waarden aannemen. In dit geval kan de uitgangsspanning slechts twee waarden aannemen: een "0" of een "1".
We kunnen de comparator ook combineren met een invertor. In dat geval gaat het lampje branden als de sensorspanning onder de referentiespanning zit.
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
| ||||||||||||
|
§3 De geheugencel
In deze paragraaf voegen we de geheugencel toe aan onze automatische systemen.
Het volgende element dat we gaan bestuderen is de geheugencel. Een geheugencel heeft twee ingangen genaamd "set" en "reset". Als er kortstondig een "1" op de "set" komt te staan, dan blijft de uitgang van de geheugencel een "1" geven, ook als de "1" op de "set" inmiddels in een "0" is veranderd. De enige manier om de geheugencel uit te zetten is door een "1" op de "reset" te zetten. In dat geval wordt het uitgangssignaal weer "0".
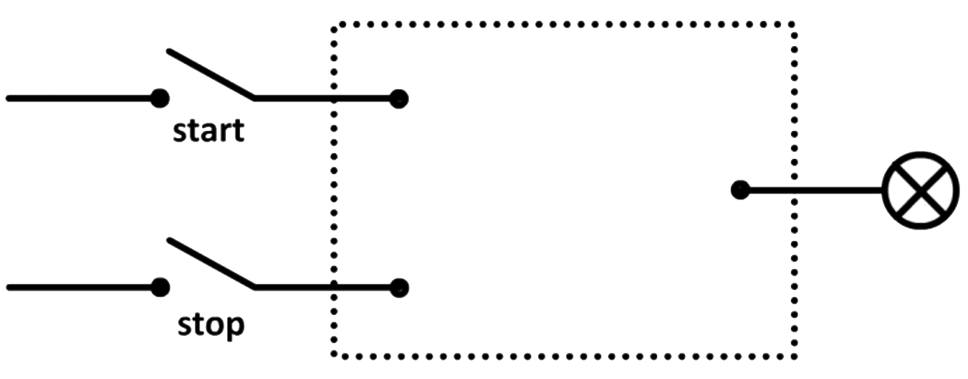
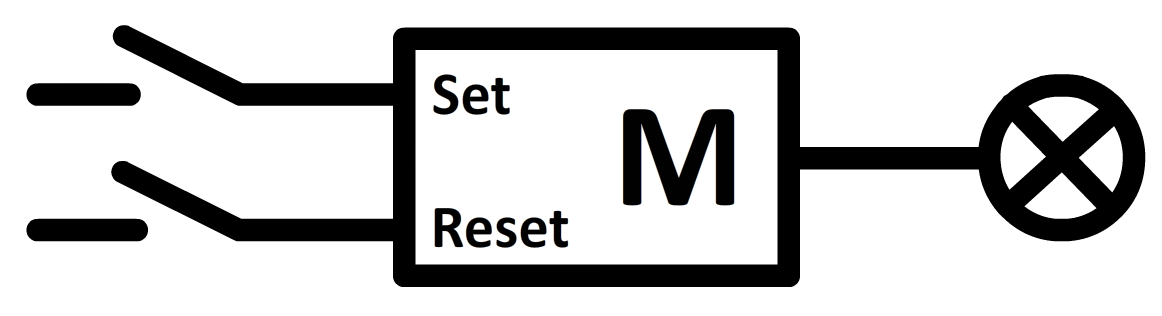
De werking van de geheugencel is gemakkelijk te begrijpen met een voorbeeldje. In het onderstaande voorbeeld gaat met een kortstondige druk op de bovenste knop een lamp aan. Deze lamp blijft branden, ook als je de knop loslaat. De lamp gaat pas uit als je de onderste knop indrukt.
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§4 De teller
In deze paragraaf voegen we de teller toe. Zoals het woord al zegt, kunnen we hier ons elektrisch systeem mee laten tellen. Dit doen we met behulp van binaire getallen.
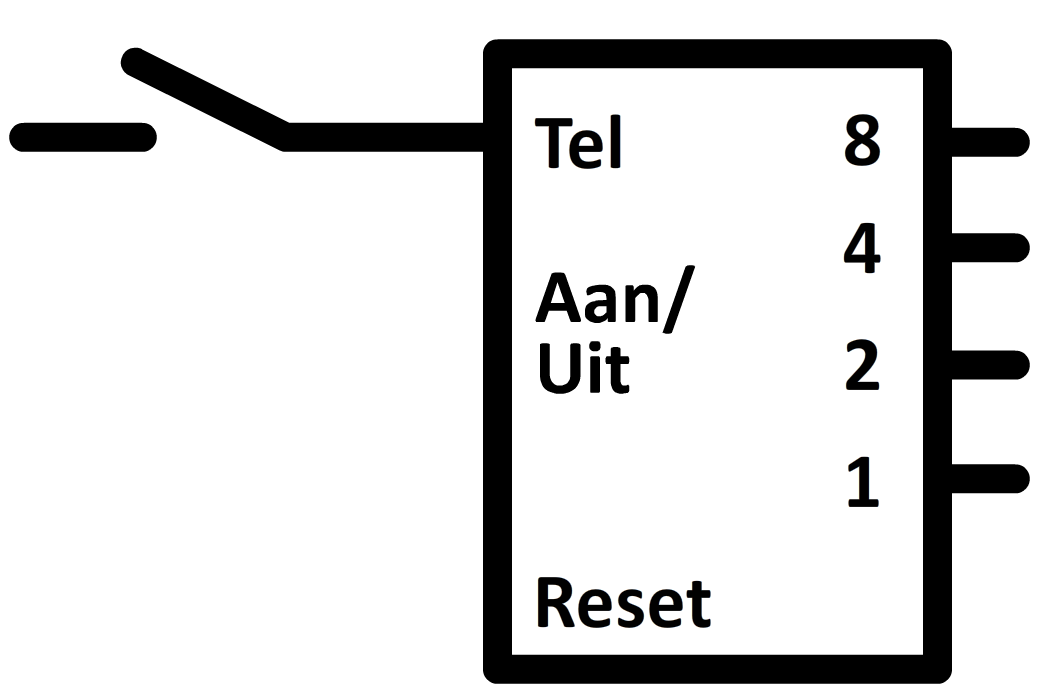
Het laatste element dat we gaan toevoegen is de teller. Als we een drukknop aansluiten op de "tel"-ingang (zie de onderstaande afbeelding), dan gaat het systeem tellen elke keer als we op de knop drukken. De getallen worden weergegeven door middel van een serie enen en nullen bij de rechter vier uitgangen. Stel dat we bijvoorbeeld zes keer op de knop hebben gedrukt, kan komt er een "1" te staan over uitgang "4" en "2", want 4 + 2 = 6. De andere uitgangen staan dan op nul.
Dit lijkt misschien een merkwaardige manier van tellen, maar er zit een idee achter. Om dit goed te begrijpen, bestuderen we eerst hoe we normaalgesproken tellen. In het dagelijks leven gebruiken we bij tellen het decimale stelsel. Dit werkt als volgt. Als we een getal nemen als "1362", dan staat het meest rechtse getal voor "2", het tweede getal van rechts voor "60", het derde getal van rechts voor "300" en het vierde getal voor "1000". De getallen in "1362" moeten we dus van rechts naar links vermenigvuldigen met 1, 10, 100 en 1000 (zie de onderstaande linker tabel).

Waar we in decimale getallen wel tien verschillende cijfers kennen (0,1,2,3,4,5,6,7,8 en 9), hebben we er bij binaire getallen maar twee (0 en 1). Een binair getal bestaat dus uit een aantal nullen en enen. Elke "0" of "1" in deze reeks wordt een bit genoemd. Een getal van één bit kan maar twee waarden aannemen ("0" of "1"). Een getal van twee bit kan vier waarden aannemen (00, 01, 10, 11). Een getal van drie bit kan wel acht waarden aannemen (000 001 010 011 100 101 110 111). Etc. Het blijkt dat een getal van "n" bit, "2n" waarden kan aannemen. Een getal van 3 bit kan dus 23 = 8 waarden aannemen. Een getal van 4-bit kan 24 = 16 waarden aannemen.
Maar nu is de vraag welke combinatie van enen en nullen hoort bij welk getal. Dit kunnen we achterhalen door de binaire getallen van rechts naar links te vermenigvuldigen met 1, 2, 4, 8 etc. (zie de onderstaande rechter tabel). Het binaire getal "1010" komt dus overeen met het decimale getal 0×1 + 1×2 + 0×4 + 1×8 = 10.

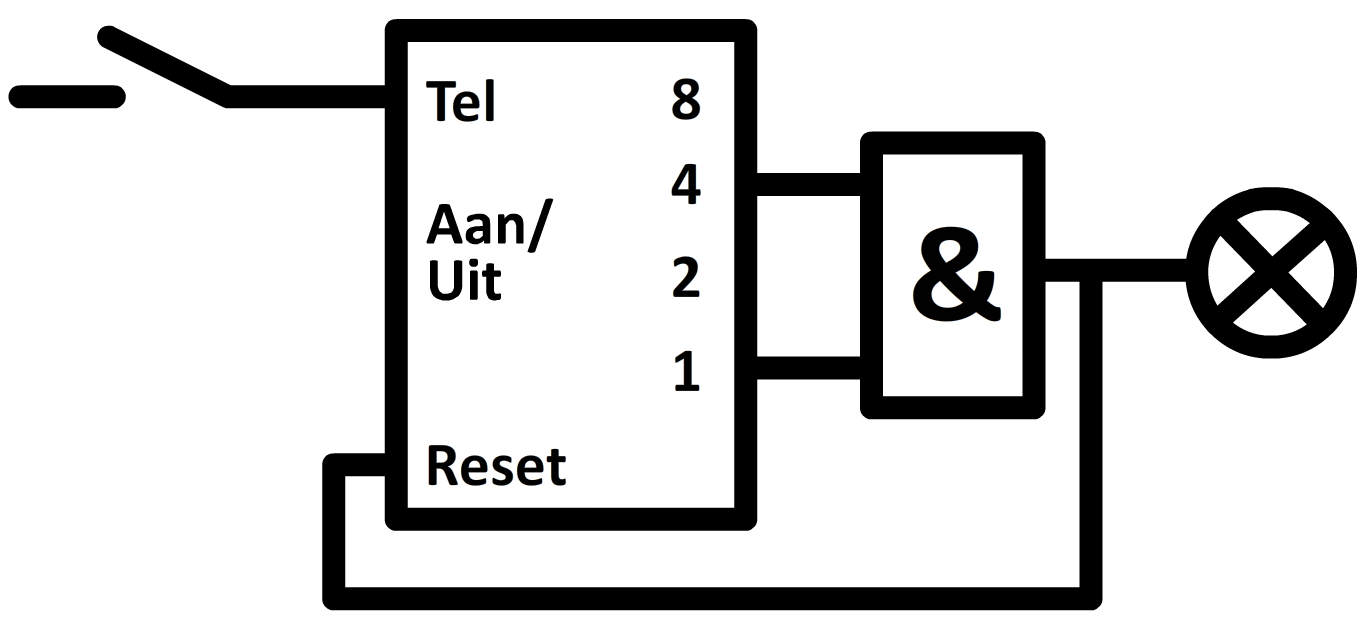
Nu terug naar de teller. Stel we willen een apparaat ontwerpen waarmee een lamp aangaat elke vijfde keer dat je een knop indrukt. In dat geval moeten we in ieder geval een EN-poort aansluiten op de "4" en de "1" uitgang, oftewel bij "0101" (zie de onderstaande afbeelding).
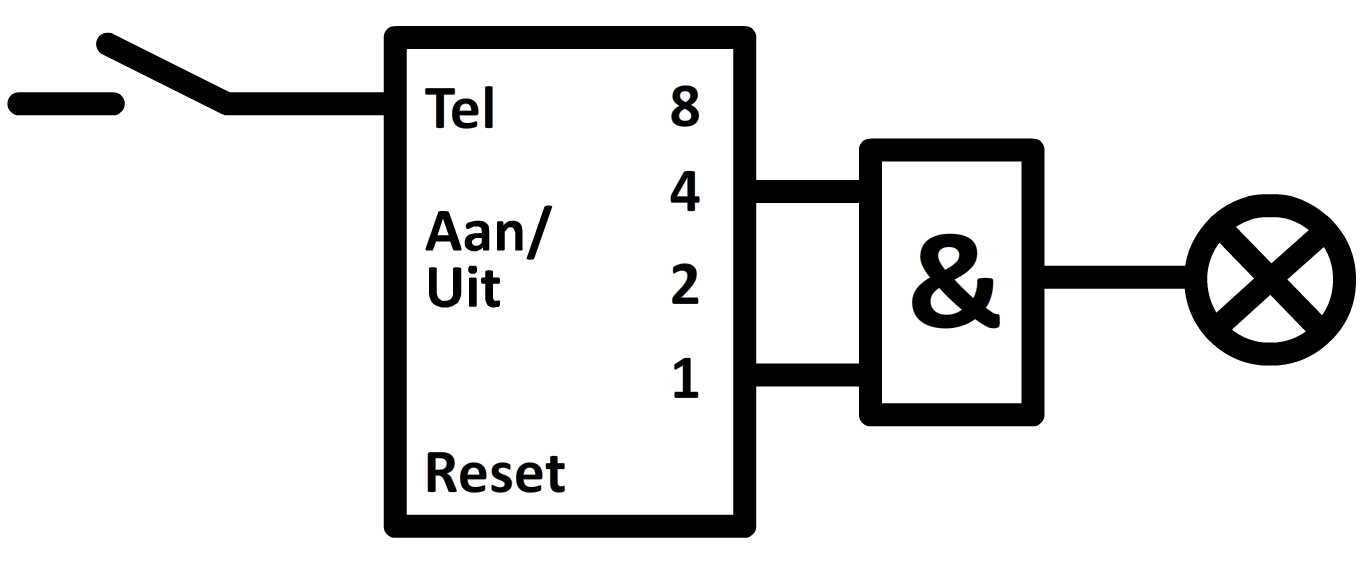
Er is wel nog een probleem met dit ontwerp. De lamp gaat nu namelijk ook aan bij "0111" (7), "1101" (13) en "1111" (15), want ook in deze gevallen vinden we een "1" bij uitgang "4" en "1". We kunnen dit probleem oplossen door de teller direct te resetten op het moment dat de lamp aangaat. De "reset"-knop zorgt ervoor dat de teller weer terugspringt naar "0000" (0) (zie de onderstaande afbeelding).
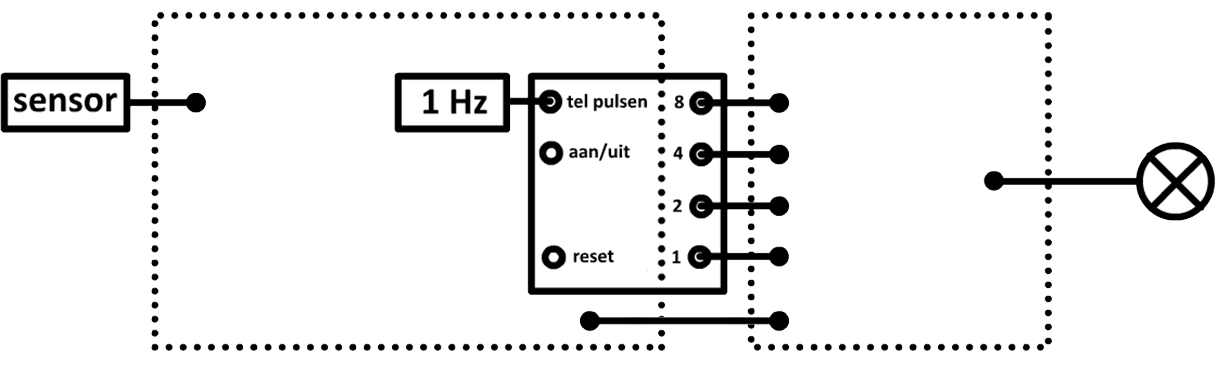
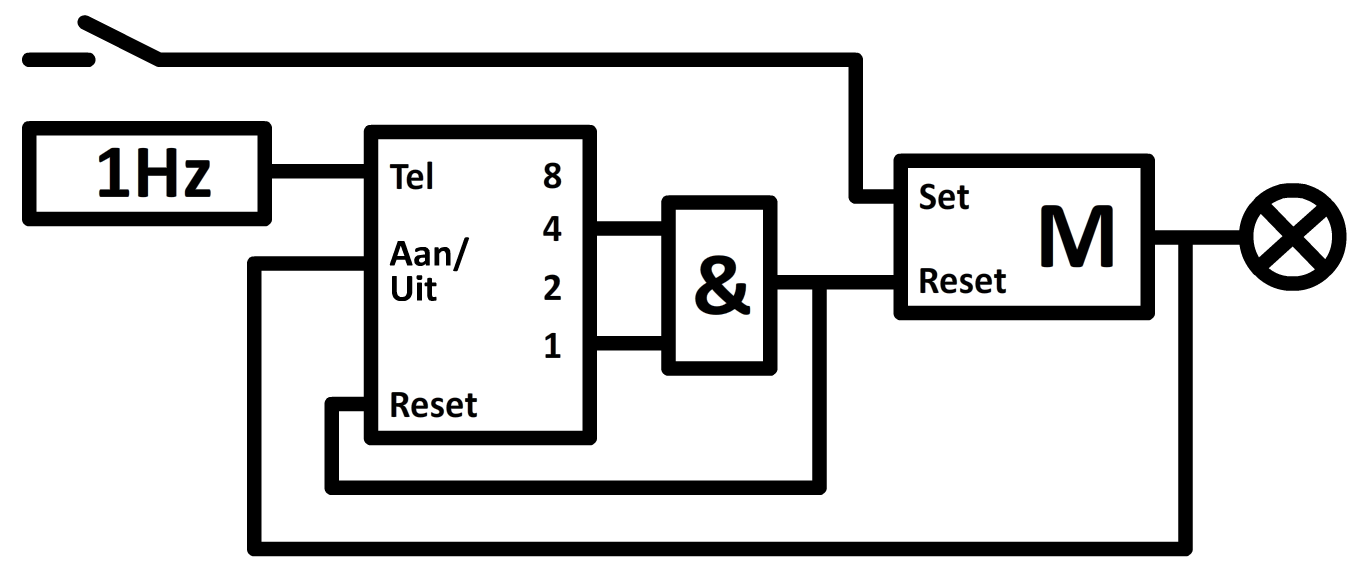
Als laatste bespreken we de "aan/uit"-ingang van de teller. Als er een stekker in deze poort zit, dan gaat de teller alleen tellen als er een "1" staat op deze ingang. In de onderstaande afbeelding is dit toegepast. We zien hier een lamp die blijvend aangaat door een knop in te drukken. Als de lamp aangaat, dan wordt ook een "1" naar de "aan/uit"-knop van de teller gestuurd. Ondertussen geeft een pulsengenerator elke seconde een "1" aan de teller. Nu de teller aanstaat, zorgen deze pulsen ervoor dat er geteld wordt. Na vijf seconden staat er een "1" op uitgang "1" en "4" en hierdoor wordt de teller en de geheugencel gereset, zodat de lamp weer uit gaat en de teller weer op "0000" komt te staan.
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|