Hoofdstuk 4
Gravitatie
§1 De vrije val §2 Cirkelbewegingen §3 Het heelal §4 De middelpuntzoekende kracht §5 Gewichtloosheid (VWO) §6 De algemene gravitatiekracht
§1 De vrije val
In dit hoofdstuk gaan we de zwaartekracht bestuderen. In de eerste paragraaf kijken we naar de valbeweging op aarde. Daarna gaan we zien hoe de zwaartekracht er ook voor kan zorgen dat objecten in een baan om bijvoorbeeld de aarde of de zon kunnen belanden.
Als een voorwerp ongehinderd valt, dan spreken we van een vrije val. Bij een vrije val werkt dus alleen de zwaartekracht op het voorwerp. Alle andere krachten, zoals wrijvingskrachten, zijn dan afwezig of verwaarloosbaar klein. Voor een vrije val geldt dus:
$$ F_{res} = F_z $$Als we deze vergelijking uitwerken met de formules "Fres = ma" en "Fz = mg", dan vinden we:
$$ ma=mg $$Door aan beide kanten de massa weg te strepen vinden we dan:
$$ a = g $$Een voorwerp dat een vrije val ondergaat heeft dus altijd een versnelling gelijk aan de valversnelling (g), ongeacht de massa van dit voorwerp. Zonder luchtwrijving zou een veer dus even snel moeten vallen als een hamer. Dit experiment is getest op de maan en dit blijkt inderdaad het geval te zijn (zie het onderstaande filmpje).
 Demonstratievideo
Demonstratievideo
| ||
|
 Demonstratievideo
Demonstratievideo
| ||
|
 Demonstratievideo
Demonstratievideo
| ||
|
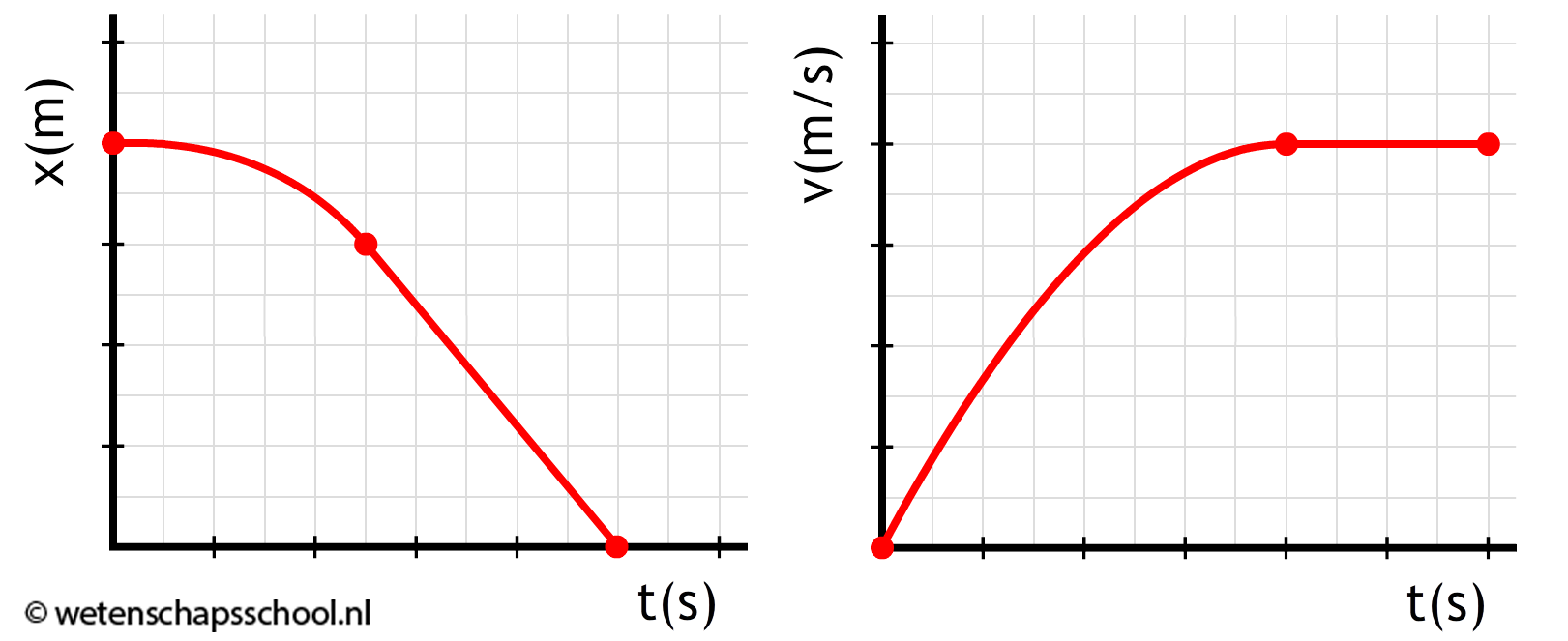
Het (v,t)-diagram van een vrije val is hieronder afgebeeld. Als we het diagram nauwkeurig aflezen, dan vinden we inderdaad dat de versnelling gelijk is aan de valversnelling (g):
$$ a = \frac{\Delta v}{\Delta t} $$ $$ a = \frac{49,05}{5,00} = 9,81 \text{ m/s}^2 $$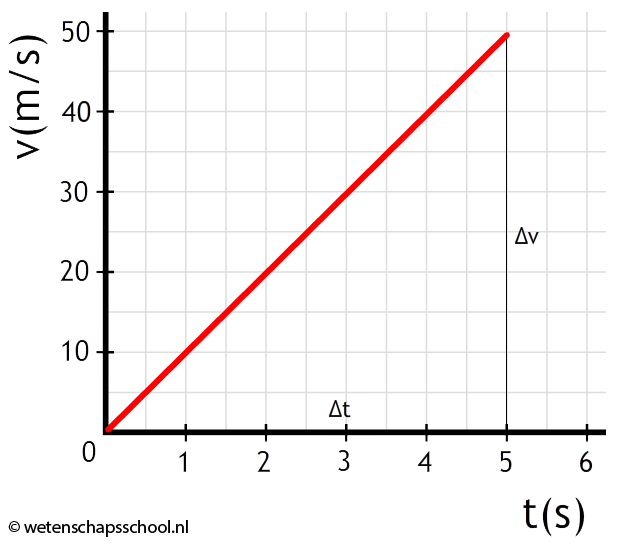
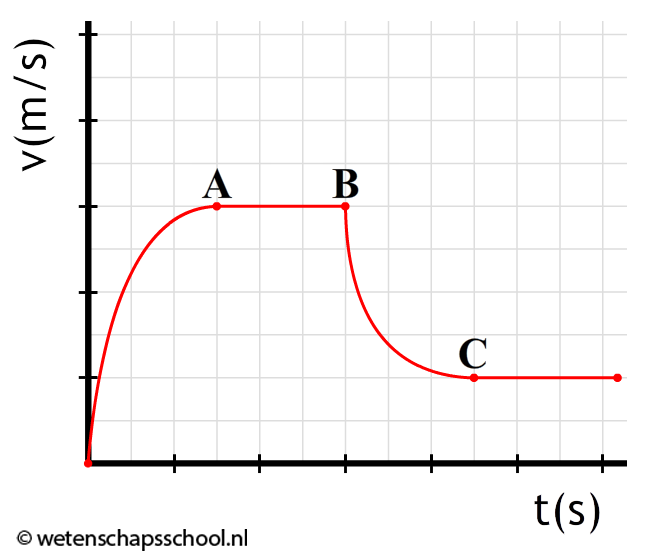
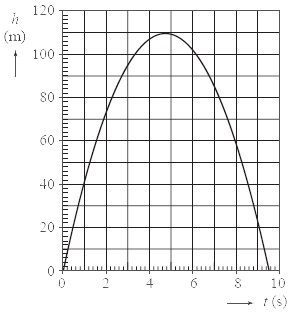
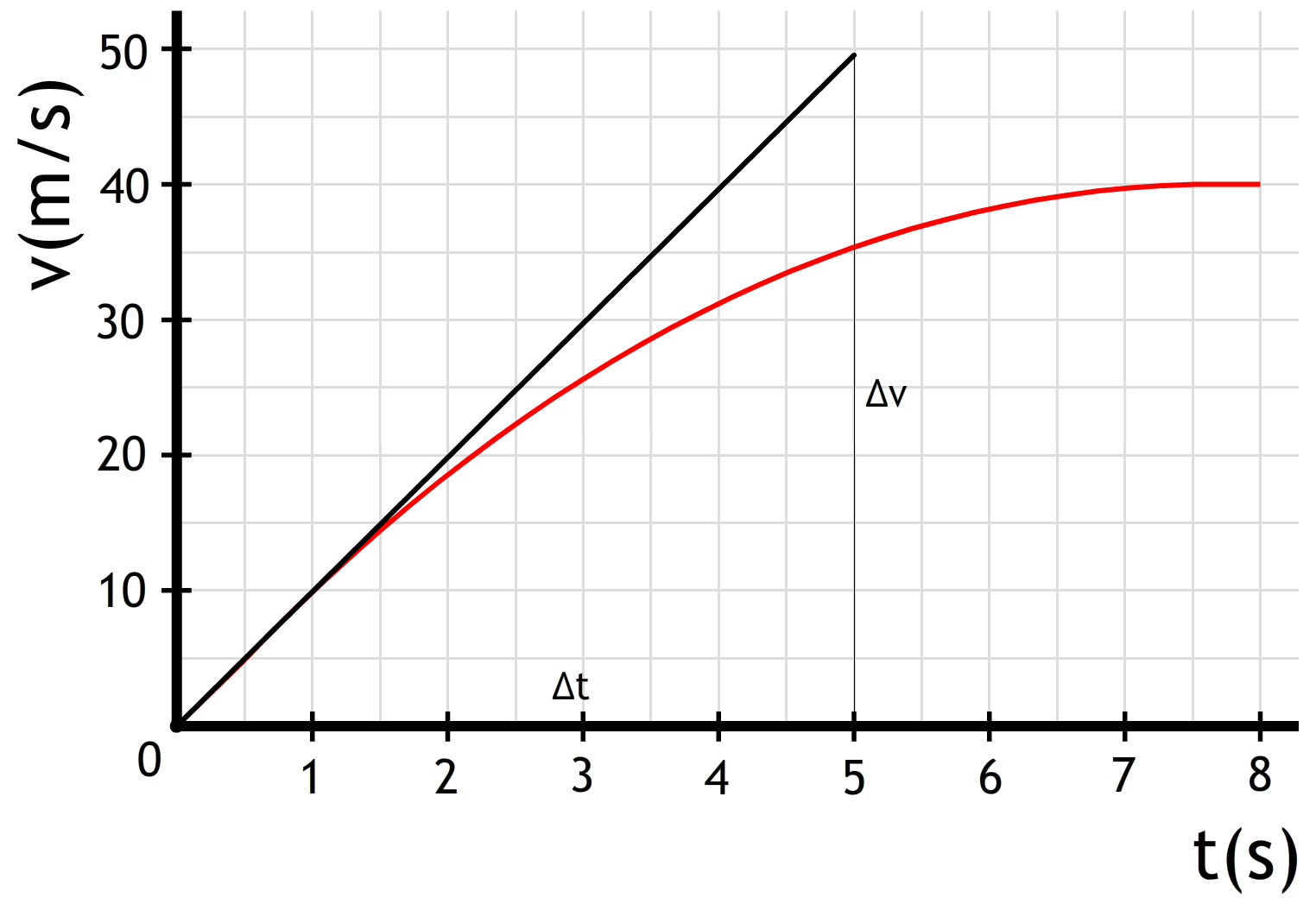
In het volgende (v,t)-diagram zien we een val waarbij de luchtwrijvingskracht niet te verwaarlozen is. Zoals je kunt zien wordt de versnelling steeds kleiner en uiteindelijk wordt de snelheid zelfs constant. Ook uit dit diagram kunnen we echter de valversnelling bepalen. Dit doen we door op t = 0 s een raaklijn te tekenen. Op dit punt is de snelheid van het voorwerp namelijk nog nul en is er dus ook geen luchtwrijvingskracht. Als gevolg hebben we op dit moment te maken met een vrije val en geldt dus ook "a = g".
 Voorbeeld
Voorbeeld
|
|
Vraag: Een persoon maakt een parachutesprong. In het eerste deel van de val is de parachute nog ingepakt. Ga na wat tijdens dit deel van de val gebeurt met de zwaartekracht, de luchtwrijvingskracht, de resulterende kracht en de versnelling. Antwoord: De zwaartekracht is volgens de formule gelijk aan "Fz = mg". De massa van de parachutespringer blijft gelijk, dus de zwaartekracht werkende op de persoon blijft ook gelijk. De luchtwrijvingskracht neemt toe doordat de snelheid van de parachutespringer toeneemt. Op de springer werk een zwaartekracht (omlaag) en een luchtwrijvingskracht (omhoog). De krachten werken dus tegen elkaar in. Hoe groter de luchtwrijvingskracht wordt, hoe kleiner de resulterende kracht hierdoor wordt. De versnelling wordt volgens de formule "a = Fnetto / m" hierdoor ook kleiner. Vraag: Leg uit dat de snelheid van de parachutespringer uiteindelijk constant zal worden. Antwoord: In eerste instantie versnelt de parachutespringer. De luchtwrijvingskracht wordt hierdoor steeds groter. Uiteindelijk wordt de luchtwrijvingskracht even groot als de zwaartekracht. In dat geval is de resulterende kracht nul. In het vorige hoofdstuk hebben we geleerd dat de snelheid dan constant is.
|
Een bijzondere eigenschap van een vrije val is dat je niet voelt dat je valt. Als je niet zou zien dat de grond op je afkomt, dan zou je denken dat je zweeft. We noemen dit gewichtloosheid.
 Demonstratievideo
Demonstratievideo
| ||
|
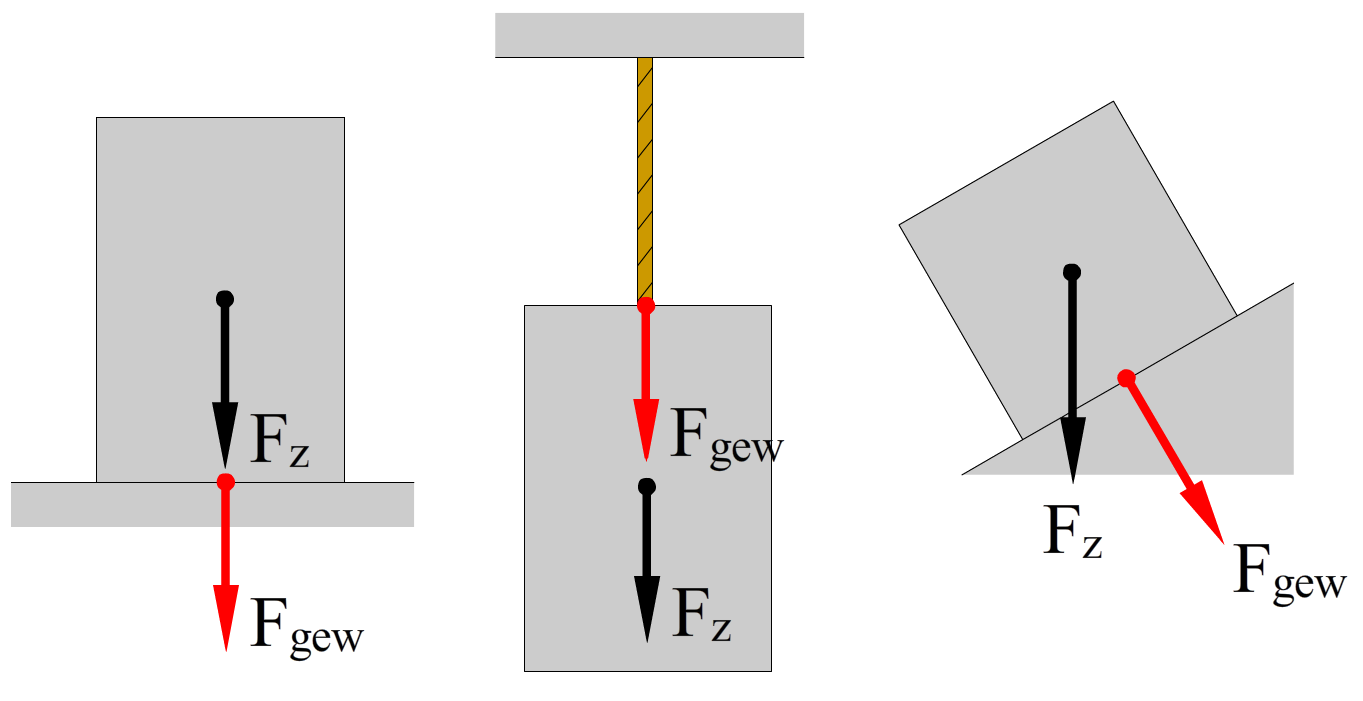
Om gewichtloosheid beter te begrijpen, definiëren we de gewichtkracht (Fgew). De gewichtkracht wordt ook wel het gewicht genoemd. In het dagelijks leven wordt gewicht vaak uitgedrukt in kilogram, maar dit is onjuist. Gewicht is een kracht en wordt dus uitgedrukt in newton. Het gewicht is de kracht die een voorwerp uitoefent op zijn ondersteuning of ophangpunt. In de eerste onderstaande afbeelding zien we een blok dat op de grond ligt. De aarde trekt een blok naar beneden (dit is de zwaartekracht). Als gevolg duwt het blok tegen de grond aan (dit is het gewicht). In de middelste afbeelding zien we een soortgelijk voorbeeld. De aarde trekt het blok naar beneden (dit is de zwaartekracht). Als gevolg trekt het blok aan het touw (dit is het gewicht). In deze twee voorbeelden zijn de zwaartekracht en de gewichtkracht even groot, maar dit is niet altijd het geval. In de derde afbeelding zien we een blok op een helling. Zoals we in het hoofdstuk kracht gezien hebben, kunnen we de zwaartekracht die op het blok werkt opdelen in een component waarmee het blok van de helling wordt geduwd en een component waarmee het blok tegen de helling aan wordt gedrukt (Fz⊥). Deze laatste component is gelijk aan de gewichtkracht (en is in evenwicht met de normaalkracht).
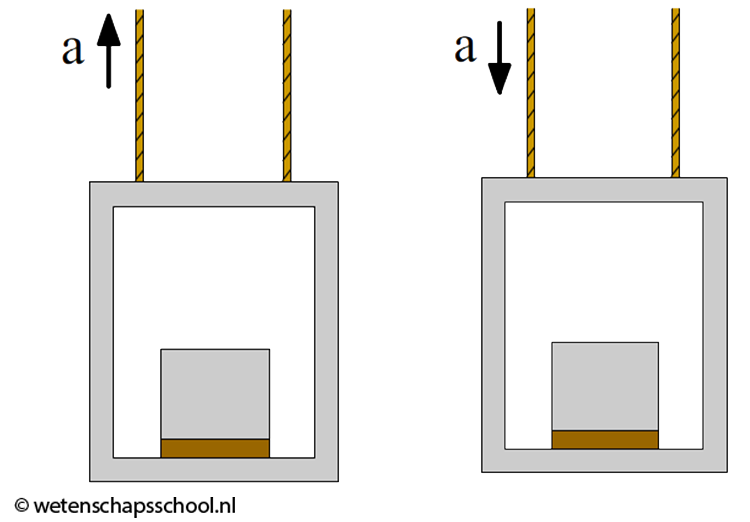
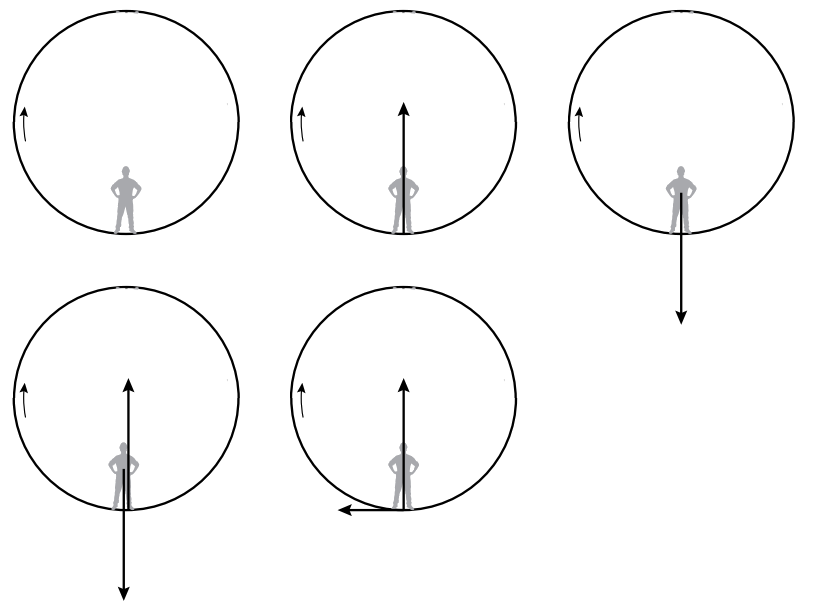
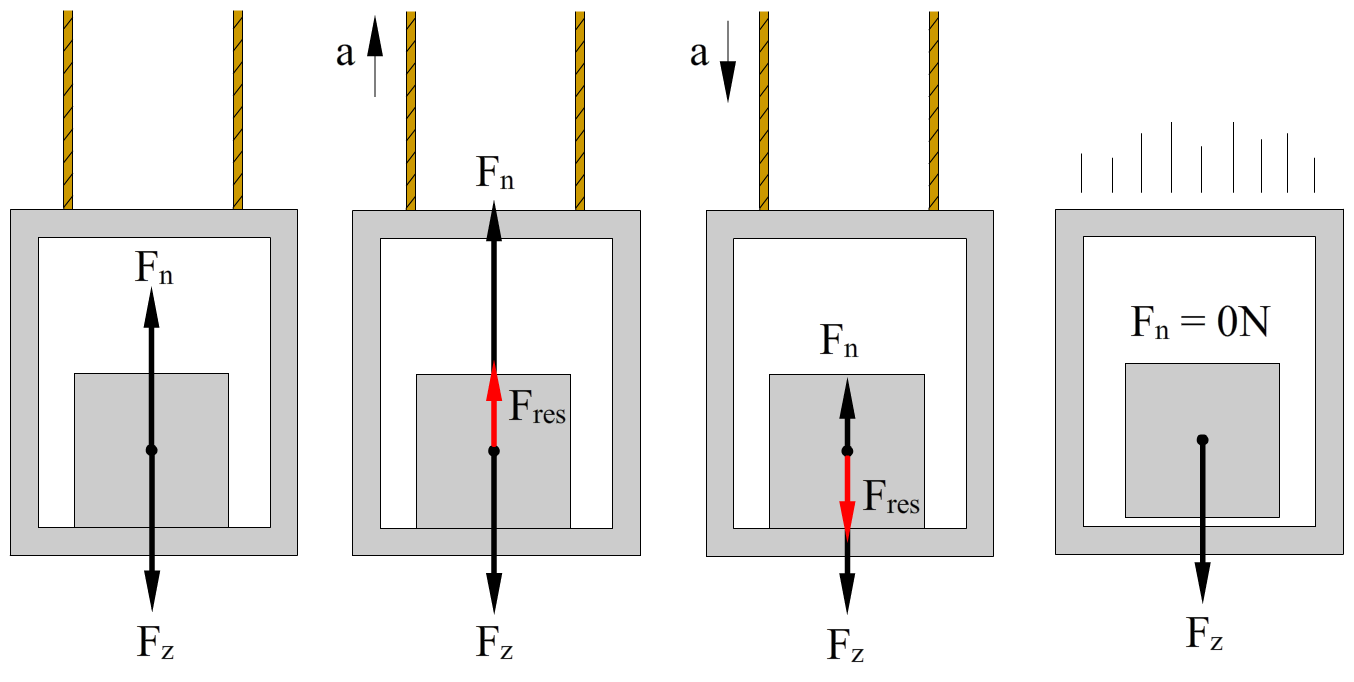
Het verschil tussen zwaartekracht en gewicht is ook duidelijk te ervaren in een lift. Hieronder zien we links een lift die stil staat of met een constante snelheid beweegt. De zwaartekracht (Fz) werkende op het blok zorgt hier voor een even grote gewichtkracht (Fgew) op de grond (deze kracht is niet afgebeeld). Dankzij de derde wet zorgt de gewichtkracht voor een even grote kracht omhoog, de normaalkracht (Fn). De zwaartekracht en de normaalkracht zijn hier dus aan elkaar gelijk. In de tweede afbeelding zien we een lift die omhoog versnelt. Er werkt in dit geval dus een resulterende kracht omhoog. Dit betekent dat de normaalkracht (omhoog) groter moet zijn dan de zwaartekracht (naar beneden). Ook hier geldt dankzij de derde wet dat de normaalkracht even groot is als het gewicht. Ook het gewicht is hier dus groter dan de zwaartekracht. Als gevolg kunnen we concluderen dat een persoon zich iets zwaarder voelt dan normaalgesproken het geval is. In de derde afbeelding versnelt een lift naar beneden en werkt er dus ook een resulterende kracht naar beneden. Als gevolg is de normaalkracht, en ook de gewichtkracht, nu kleiner. Dit zorgt ervoor dat we ons iets lichter voelen als een lift naar beneden versnelt. In de rechter afbeelding versnelt de lift naar beneden met de valversnelling (g). In dat geval hebben we te maken met een vrije val en is de resulterende kracht gelijk aan de zwaartekracht. Als gevolg moet de normaalkracht, en dus ook het gewicht, hier nul zijn. Het blok is dan dus gewichtloos.
 Demonstratievideo
Demonstratievideo
| ||
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
(bron: examen VWO 2015-1)
(bron: examen VWO 2011-1)
|
§2 Cirkelbewegingen
In de komende twee paragrafen gaan we de theorie uit het hoofdstuk "Beweging" en "Kracht" uitbreiden, zodat we hier ook cirkelbewegingen mee kunnen beschrijven. Dit stelt ons in staat om bijvoorbeeld de beweging van de aarde om de zon te begrijpen. In deze paragraaf bestuderen we de cirkelbeweging. In een latere paragraaf kijken we naar de kracht die hiervoor nodig is.
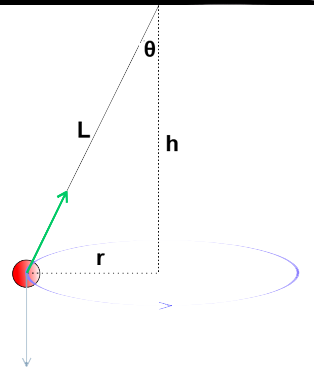
In hoofdstuk "Beweging" en "Kracht" hebben we rechtlijnige bewegingen bestudeerd. In dit hoofdstuk gaan we voorwerpen bestuderen die een bocht maken. Denk bijvoorbeeld aan een auto die de bocht door gaat of de beweging van de aarde om de zon. Om bochten goed te begrijpen bestuderen we eerst de cirkelbeweging. Hieronder zien we bijvoorbeeld een massa "m", die een cirkelbeweging maakt om een middelpunt "M". De afstand tussen "m" en "M" blijft gedurende de beweging constant. We noemen deze afstand de baanstraal (r).
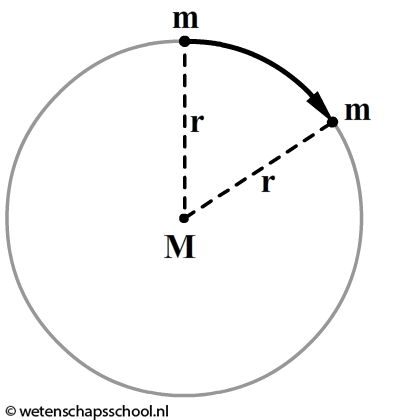
Zoals altijd vinden we de snelheid van een voorwerp door de afgelegde afstand te delen door de tijdsduur. De afgelegde weg van één omwenteling is gelijk aan de omtrek van de cirkel (2πr). De tijd die nodig is voor een omwenteling noemen we de omlooptijd (T). De snelheid van massa "m" wordt dus gegeven door:
$$ v = \frac{2\pi r}{T} $$
|
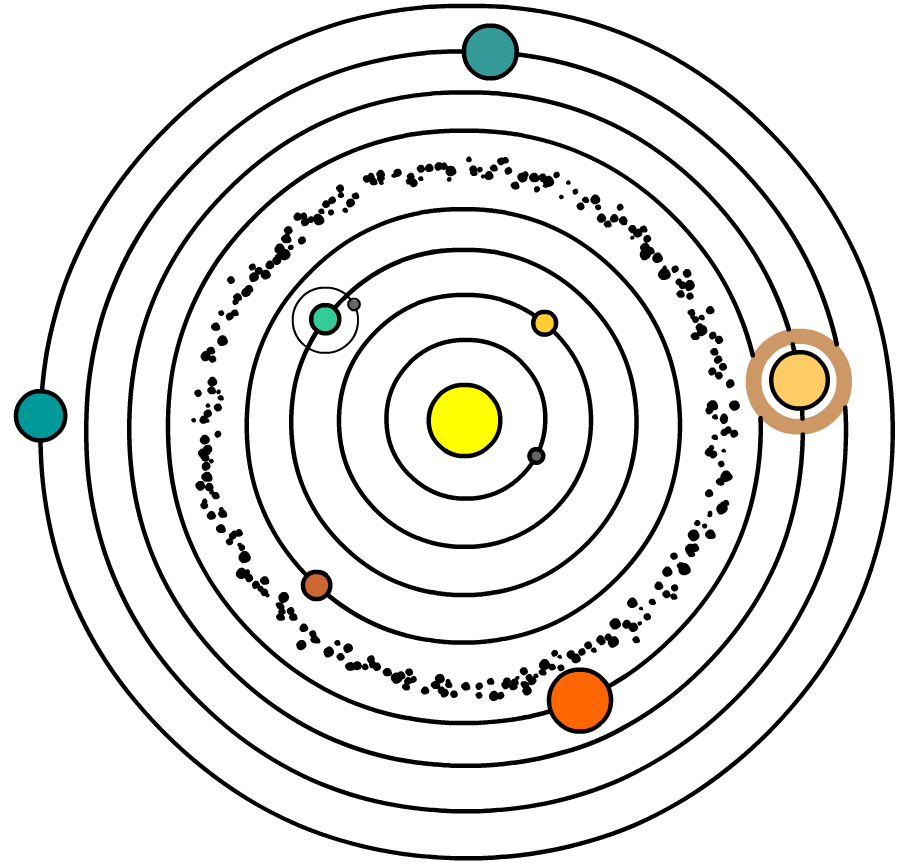
Cirkelbewegingen komen veel voor in de ruimte. Veel planeten in ons zonnestelsel maken bijvoorbeeld nagenoeg een cirkelbeweging om de zon (zie de onderstaande linker afbeelding). In BINAS kan je gegevens vinden over de banen van verschillende planeten. Let er bij de opdrachten goed op of je de straal van de planeet nodig hebt (de afstand van het middelpunt van de planeet tot het oppervlak) of de baanstraal van de planeet (de afstand van het midden van de planeet tot het midden van de zon).
Een ander voorbeeld van een object dat een cirkelbaan maakt is een satelliet. Satellieten worden bijvoorbeeld gebruikt om tv-kanalen te ontvangen met een satellietschotel. Om ervoor te zorgen dat de satellietschotel telkens naar de satelliet blijft wijzen, is het nodig dat de satelliet precies meedraait met de aarde. Deze satellieten hebben dus een omlooptijd van 24 uur. Satellieten met deze omlooptijd worden geostationaire satellieten genoemd.
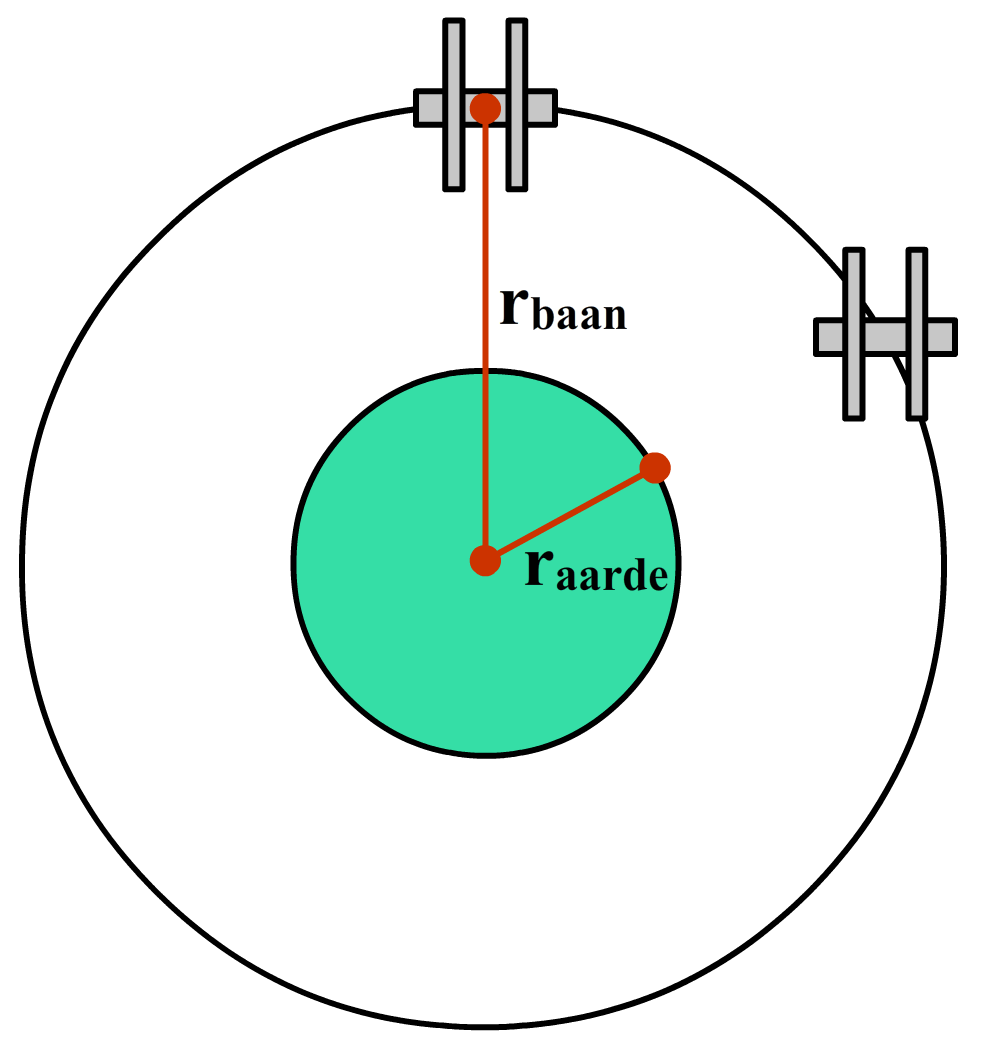
Geostationaire satellieten bevinden zich 35786 km boven het aardoppervlak. We kunnen hiermee de baanstraal (r) vinden door de straal van de aarde hierbij op te tellen (zie de onderstaande afbeelding). Volgens BINAS is de straal van de aarde gelijk aan 6,371 × 106 m. We vinden hiermee:
r = 35,786 × 106 + 6,371 × 106 = 42,157 × 106 m
Naast de omlooptijd, gaan we in deze paragraaf ook rekenen met het toerental, hetgeen vaak gemeten wordt in rpm (dit staat voor "revolutions per minute" of in het Nederlands "omwentelingen per minuut"). Stel dat een wasmachine een toerental heeft van 1500 rpm, dan kunnen we met behulp van een verhoudingstabel gemakkelijk de omlooptijd T in seconden vinden:
|
1500 omwentelingen |
1 omwenteling |
|
60 seconden |
... seconden |
We vinden dan T = 1 × 60 / 1500 = 0,04000 s.
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§3 Het heelal
In het heelal komen cirkelbewegingen vaak voor. Denk bijvoorbeeld aan het bewegen van de maan om de aarde en de aarde om de zon. In deze paragraaf bespreken we een aantal van deze bewegingen
In de onderstaande linker afbeelding zien we tussen de planeet Mars en Jupiter de asteroïdengordel. Deze gordel bestaat uit allemaal brokstukken en een paar dwergplaneten, waarvan Ceres de grootste is. Het kan gebeuren dat één van deze brokstukken richting de aarde schiet. Een steen die vanuit de ruimte op aarde terecht komt noemen we een meteoriet. Een kleine meteoriet doet meestal geen schade, maar de meteoriet die 65 miljoen jaar geleden met de aarde botste had een diameter van ongeveer 10 km en heeft ervoor gezorgd dat de dinosauriërs zijn uitgestorven.
Ook bewegen er een aantal kometen in ons zonnestelsel. Een komeet is een object bestaande uit ijs, stof en steen. Het ijs van de komeet smelt door de zon en zorgt dat kometen vaak een staart hebben (zie de rechter afbeelding).


Om veel sterren draaien ook planeten. We noemen dit exoplaneten. Het ziet er niet naar uit dat we deze planeten snel zullen bereiken. De dichtstbijzijnde ster is namelijk zo’n 4,35 lichtjaren (4,35 lj) van ons vandaan. Een lichtjaar is gelijk aan de afstand die licht aflegt in een jaar. Volgens BINAS geldt dat 1 lj = 9,461 × 1015 m.
De afstanden binnen het zonnestelsel zijn wel haalbaar. In 1969 lukte het de mens voor het eerst om op de maan te landen. Hoewel de mens nog nooit op een andere planeet heeft gestaan, is het wel gelukt om robotjes te sturen naar verschillende hemellichamen in ons zonnestelsel. Afstanden meten we in dat geval vaak in astronomische eenheden (AE). 1 AE is gelijk aan de afstand van de aarde tot de zon, oftewel 1,49598 × 1011 m.
Een andere bekende cirkelbeweging in het zonnestelsel is de baan van de maan om de aarde. Ook andere planeten hebben manen. Hieronder zien we bijvoorbeeld de vier manen van Jupiter.

In de onderstaande afbeelding zien we de maan in zijn baan om de aarde. Ook zien we de zon die zowel de aarde als de maan verlicht. Aan de donkere kant van de aarde is het nacht en aan de lichte kant is het dag. Doordat de aarde om zijn eigen as draait, wisselen dag en nacht elkaar elke 24 uur af.
De maan wordt in zijn baan om de aarde telkens vanaf dezelfde kant verlicht, maar vanaf de aarde gezien is telkens een wisselende hoeveelheid van de donkere en lichte kant te zien. Dit zorgt voor de verschillende fasen van de maan. Als de maan zich tussen de zon en aarde bevindt, dan zien we alleen de donkere kant van de maan. We noemen dit de nieuwe maan. Als de maan zich aan de andere kant van de aarde bevindt, dan zien we een volledig verlichte maan. We noemen dit de volle maan. Tussen deze posities in zien we de maan deels verlicht en deels donker.
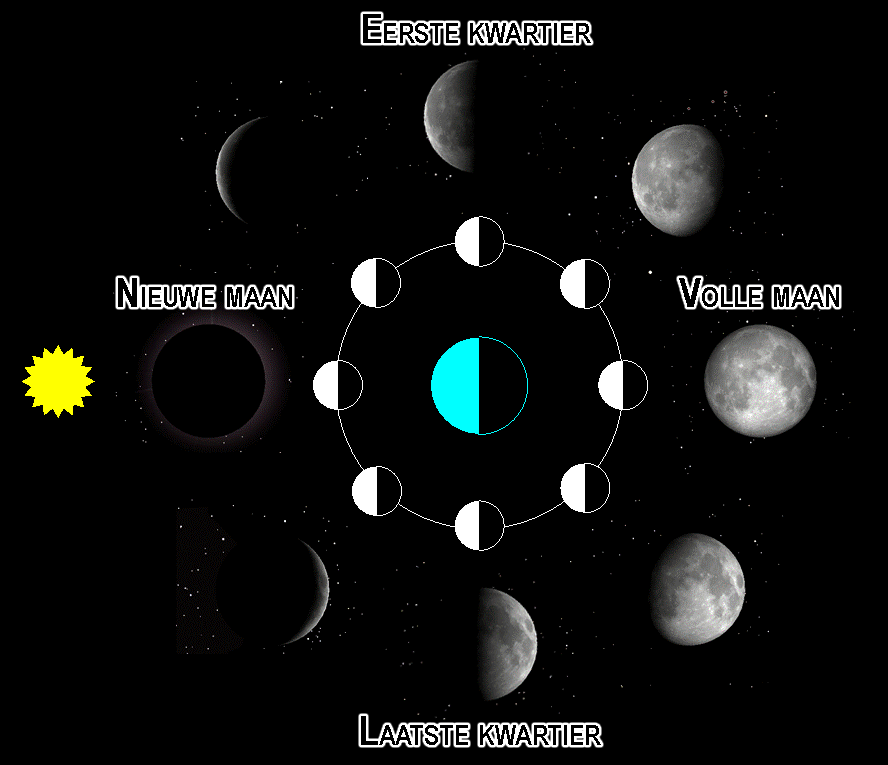
Wellicht dat je je afvraagt hoe we ooit een volle maan zien. Het lijkt in de bovenstaande afbeelding immers dat bij volle maan het licht van de zon geblokkeerd zal worden door de aarde, en de maan dus helemaal niet zou bereiken. Dat dit niet het geval is, kunnen we goed zien door de bovenstaande afbeelding eens van de zijkant te bekijken (zie de onderstaande afbeelding). We zien hier dat de baan de maan onder een hoek staat. Als gevolg kan de zon toch voor een volle maan zorgen.
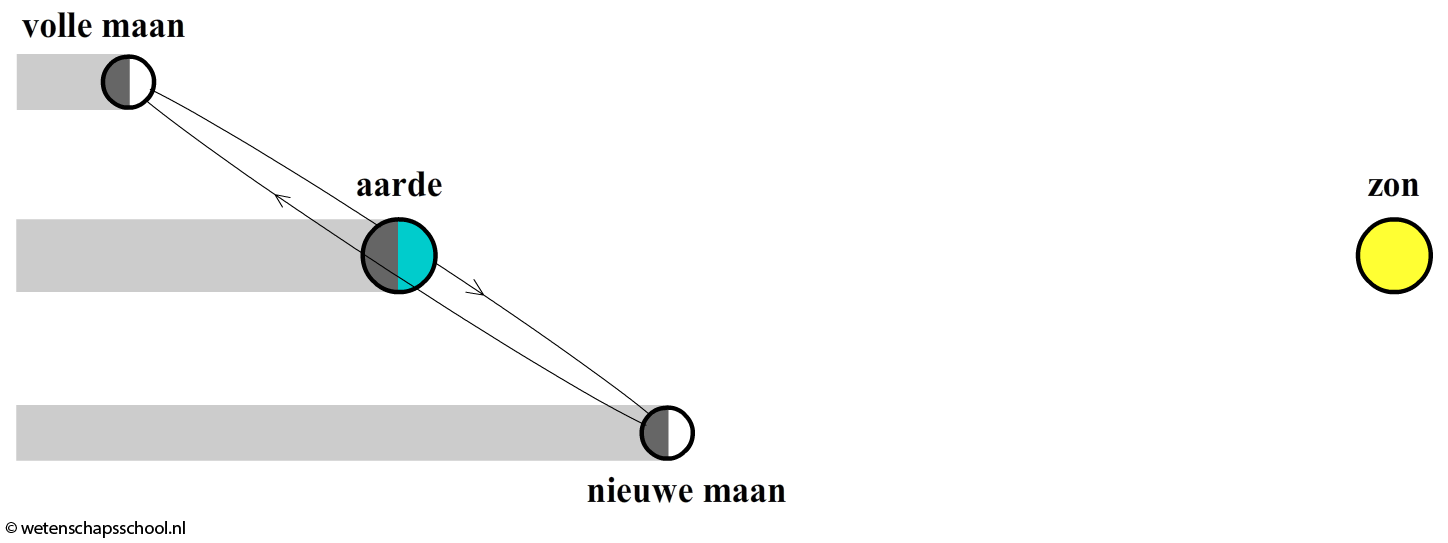
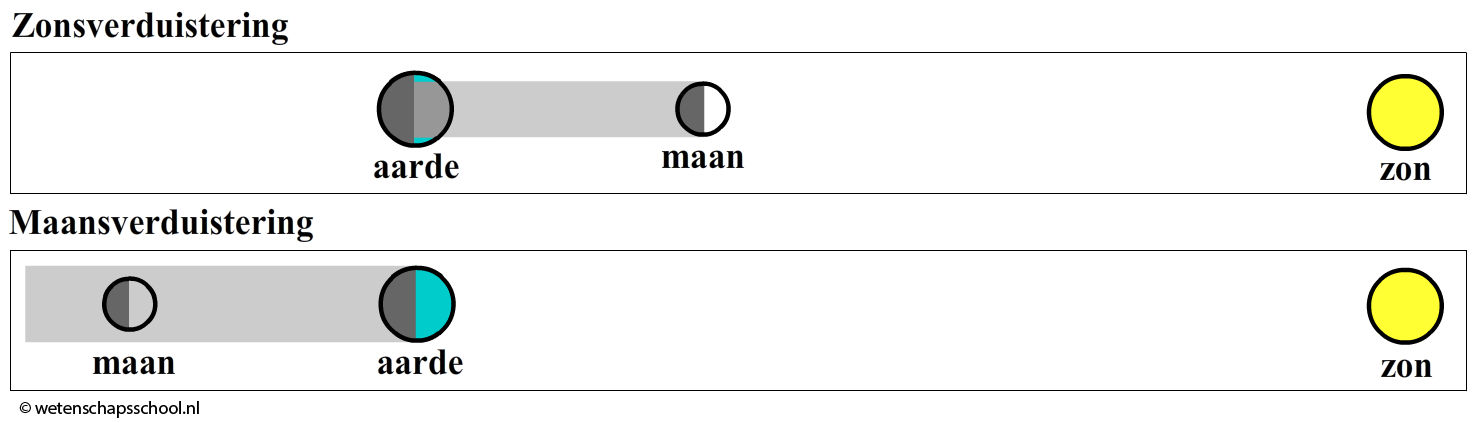
Af en toe staat de maan echter wel precies achter de aarde of tussen de zon en de aarde. Als de maan zich precies tussen de zon en de aarde bevindt, dan vindt een zogenaamde zonsverduistering plaats (zie de eerste onderstaande afbeelding). Het licht van de zon wordt hier geblokkeerd door de maan. De maan kan ook door de schaduw van de aarde trekken. In dat geval spreken we van een maansverduistering (zie de tweede afbeelding).
In de onderstaande foto zien we de maan die trekt door de schaduw van de aarde tijdens een maansverduistering.

In de onderstaande foto's zien we links een zonsverduistering en rechts zien we de schaduw die de maan door de zonsverduistering op de aarde werpt.

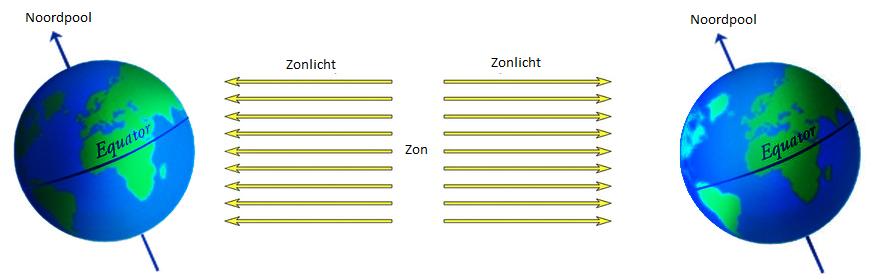
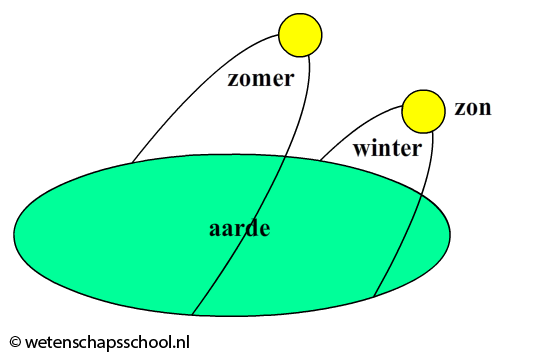
De seizoenen ontstaan doordat de as van de aarde onder een hoek staat. Dit is goed te zien in de onderstaande linker afbeelding. Als de aarde in deze afbeelding links van de zon staat, dan wordt de onderkant van de aarde iets beter verlicht dan de bovenkant. Het is nu in het zuidelijk halfrond zomer en in het noordelijk halfrond winter. Als de aarde rechts van de zon staat, dan wordt de bovenkant iets beter verlicht dan de onderkant. Nu is het juist in het noordelijk halfrond zomer. Vanaf de aarde zien we ditzelfde effect doordat de baan van de zon in de zomer hoger boven de horizon staat. In de rechter afbeelding is dit te zien.
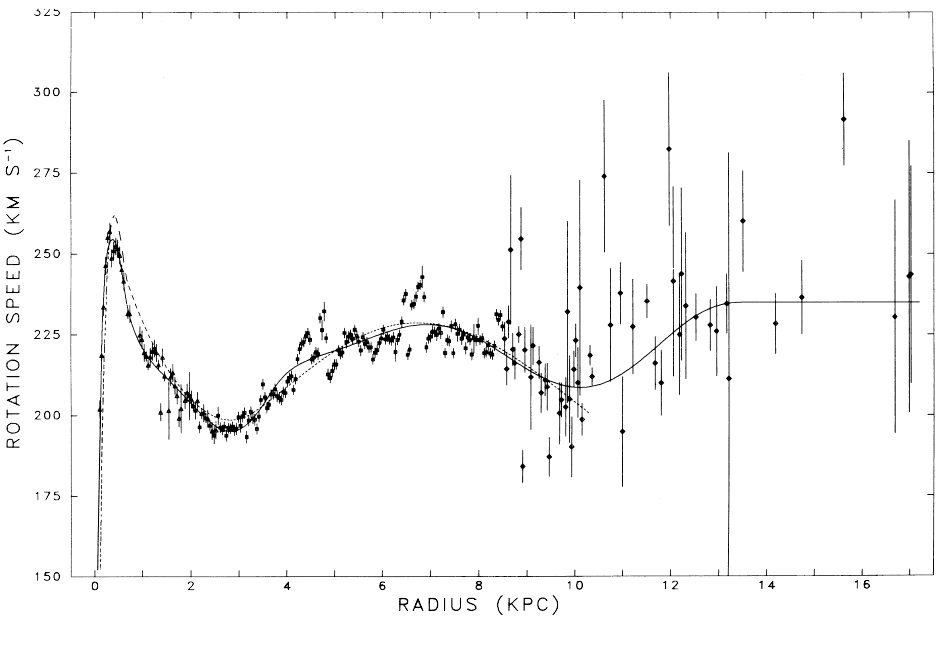
Er zijn ook cirkelbewegingen te vinden op nog grotere schaal. Onze zon is slechts één ster in een gigantisch melkwegstelsel, ook wel een sterrenstelsel genoemd, bestaande uit miljarden sterren. Hieronder is een foto van zo'n melkwegstelsel te zien. Al deze sterren maken cirkelbewegingen om het centrum van dit melkwegstelsel. In het centrum bevindt zich een superzwaar zwart gat. Een zwart gat is een object dat zo zwaar is dat zelfs licht er niet aan kan ontsnappen. Door de sterren te bestuderen die rond dit zwarte gat bewegen (zie de rechter afbeelding), is achterhaald dat het zwarte gat een massa moet hebben gelijk aan 4 miljoen keer de massa van de zon.


In de onderstaande afbeelding zien we een enorme hoeveelheid melkwegstelsels, elk bestaande uit miljarden sterren. Melkwegstelsels die ver van elkaar af staan, bewegen langzaam uit elkaar. Hieruit blijkt dat het heelal steeds groter aan het worden is. We noemen dit ook wel het uitdijen van het heelal. Omdat het heelal steeds groter aan het worden is, moet het dus in het verleden kleiner geweest zijn. Door de snelheid van het uitzetten te achterhalen, is het wetenschappers gelukt om uit te rekenen wanneer het hele heelal zich in één punt bevond. Uit dit punt is het hele heelal ontstaan. We noemen dit de oerknal.

 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§4 De middelpuntzoekende kracht
In deze paragraaf bestuderen we de kracht die nodig is om een object in een cirkelbaan te houden. We noemen dit de middelpuntzoekende kracht.
In de vorige paragraaf hebben we geleerd over cirkelbewegingen, maar hoe krijgen we een voorwerp in een cirkelbaan? Dit doen we door een kracht uit te oefenen loodrecht op de bewegingsrichting van het voorwerp. We zien dit gebeuren in de onderstaande linker afbeelding. Rechts is een voorwerp afgebeeld dat in een cirkelbaan beweegt. Merk op dat de kracht wederom loodrecht op de bewegingsrichting staat en dat de kracht hierdoor naar het middelpunt van de cirkelbaan wijst. We noemen een dergelijke kracht daarom ook wel een middelpuntzoekende kracht (Fmpz).
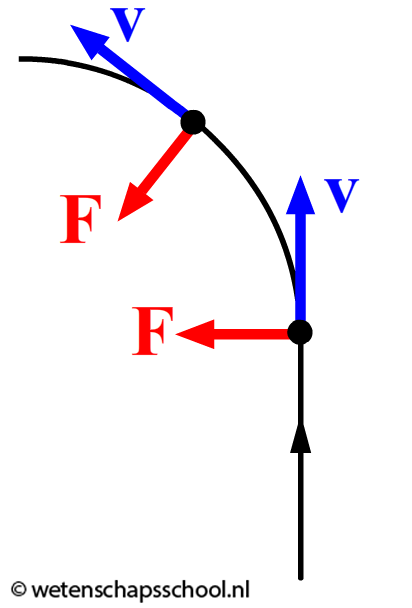

We kunnen deze beweging als volgt begrijpen. Volgens de eerste wet van Newton bewegen ongehinderde voorwerpen met een constante snelheid en in een rechte lijn. We noemen dit ook wel een eenparige beweging. Een voorwerp dat een cirkelbeweging maakt, zou dus 'het liefst' op elk moment rechtdoor willen bewegen. De middelpuntzoekende kracht trekt het voorwerp echter elk moment terug richting het middelpunt van de cirkel. Op deze manier blijft het voorwerp in zijn cirkelbaan.
In de extra paragraaf aan het eind van dit hoofdstuk zullen we bewijzen dat voor het maken van een cirkelbeweging de grootte van deze kracht altijd gelijk moet zijn aan:
$$ F_{mpz} = \frac{mv^2}{r} \;\;\;\;\;\;\;\;\; \text{Gebruik altijd SI-eenheden}$$
|
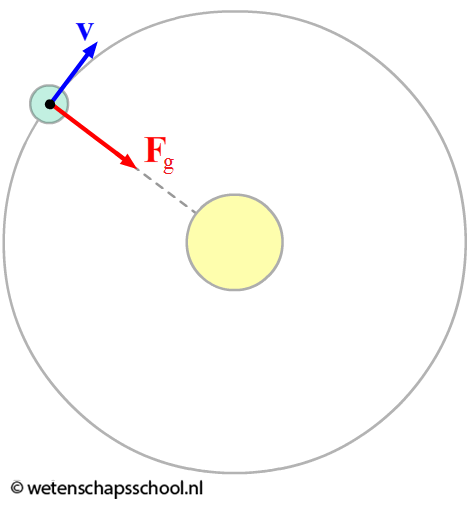
Het is belangrijk om te realiseren dat de middelpuntzoekende kracht niet een nieuwe soort kracht is. Het is de kracht die nodig is om een voorwerp in zijn baan te houden en dit kan in principe door elke kracht gedaan worden. Als we een steen horizontaal rondslingeren aan een touw, dan is het bijvoorbeeld de spankracht in het touw die ervoor zorgt dat de steen in zijn baan blijft. We zeggen in dat geval dat de middelpuntzoekende kracht geleverd wordt door de spankracht. Een ander voorbeeld is het draaien van de aarde om de zon (zie de afbeelding linksonder). Ook hier werkt een middelpuntzoekende kracht. In dit geval wordt deze kracht geleverd door de zwaartekracht (ook wel de gravitatiekracht genoemd).
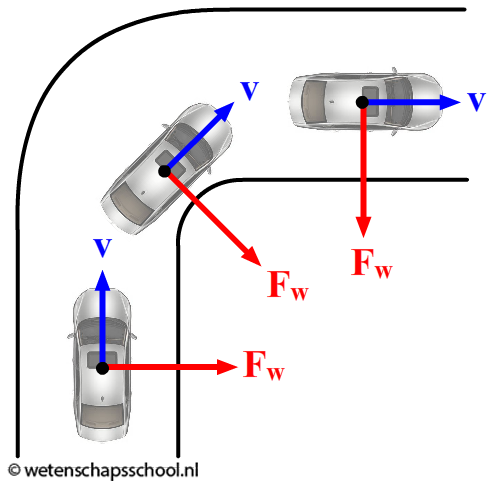
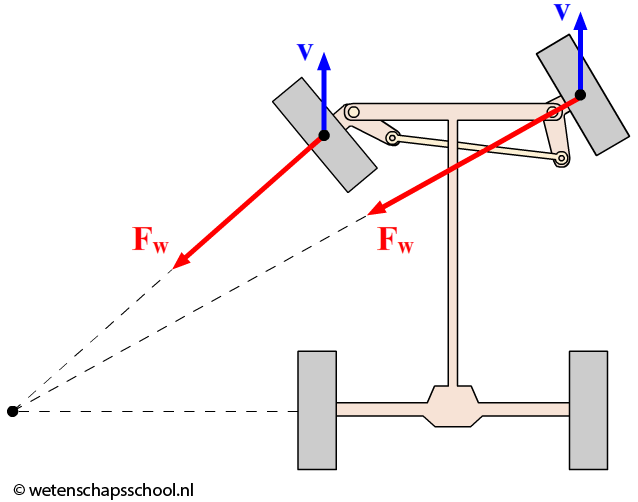
Er werkt ook een middelpuntzoekende kracht als een auto een bocht maakt. In dit geval wordt de middelpuntzoekende kracht geleverd door de wrijvingskracht tussen de wielen en de weg (zie de middelste onderstaande afbeelding). Deze extra wrijvingskracht wordt veroorzaakt doordat de bestuurder de voorwielen van de auto draait. De auto "wil" rechtdoor, maar de wrijvingskracht forceert de auto in een cirkelbeweging. In de rechter afbeelding kan je zien dat auto's zo ontworpen zijn dat de wrijvingskracht op elk wiel naar hetzelfde middelpunt wijst.
 Demonstratievideo
Demonstratievideo
|
|
In het onderstaande filmpjes zien we dit effect. We zien o.a. dat bekerglazen met vloeistof over de kop geslingerd worden. De vloeistoffen blijven netjes in de glazen zitten. In dit geval is het de normaalkracht van de bodem van de glazen die de vloeistoffen in hun baan houden. |
Als inzittende van een auto lijkt het alsof je bij het maken van een bocht naar de buitenbocht wordt geduwd. Dit is echter een illusie! Wat er gebeurt, is dat de inzittenden in een rechte lijn willen voortbewegen, terwijl de auto de bocht om gaat. Het is dus niet zo dat je naar de buitenbocht wordt geduwd, maar juist dat de auto je de bocht in trekt!
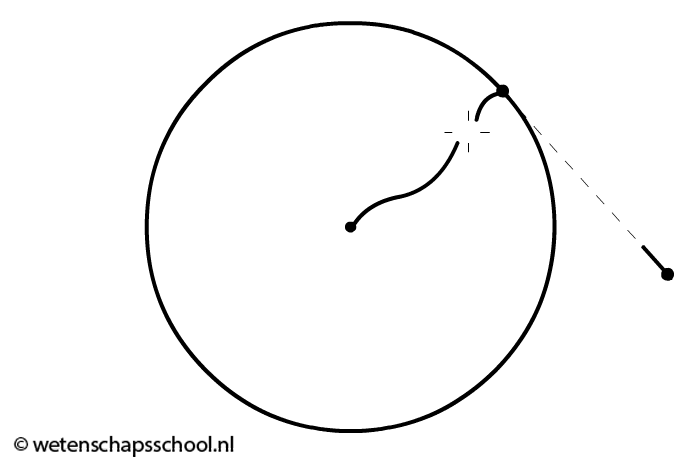
Hetzelfde geldt voor het horizontaal rondslingeren van een steen aan een touw. Het lijkt alsof de steen een kracht naar buiten uitoefent, maar in werkelijkheid probeert de steen alleen maar rechtdoor te bewegen en is het jouw spierkracht die de steen in de cirkelbaan houdt. Als op een bepaald moment de middelpuntzoekende kracht zou wegvallen (bijvoorbeeld als het touw breekt), dan zou het voorwerp (volgens de eerste wet van Newton) wegschieten in een rechte lijn in de richting die het op dat moment heeft. Het voorwerp schiet dan dus weg langs een raaklijn van de cirkelbaan (zie de onderstaande linker afbeelding).
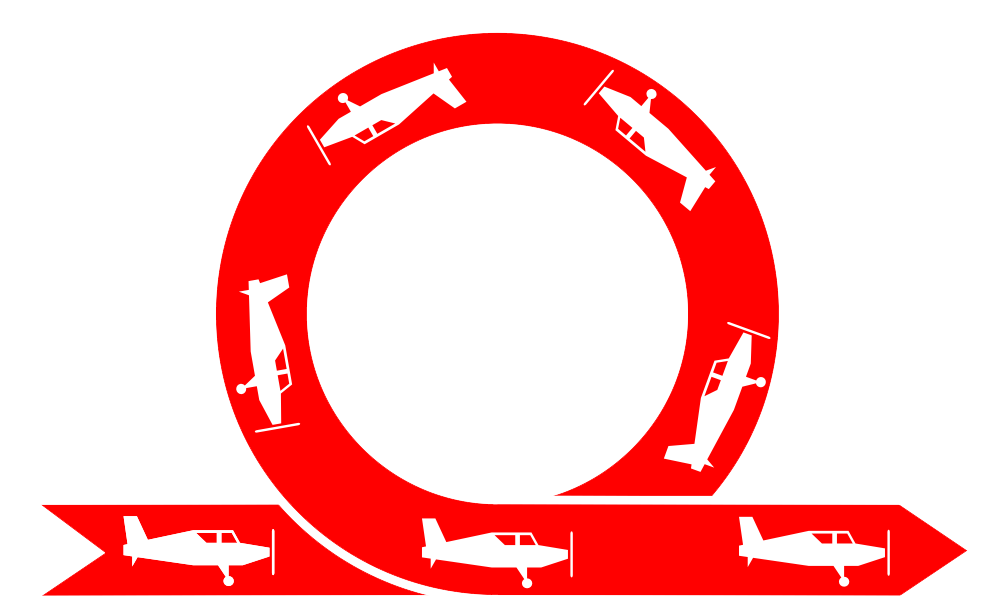
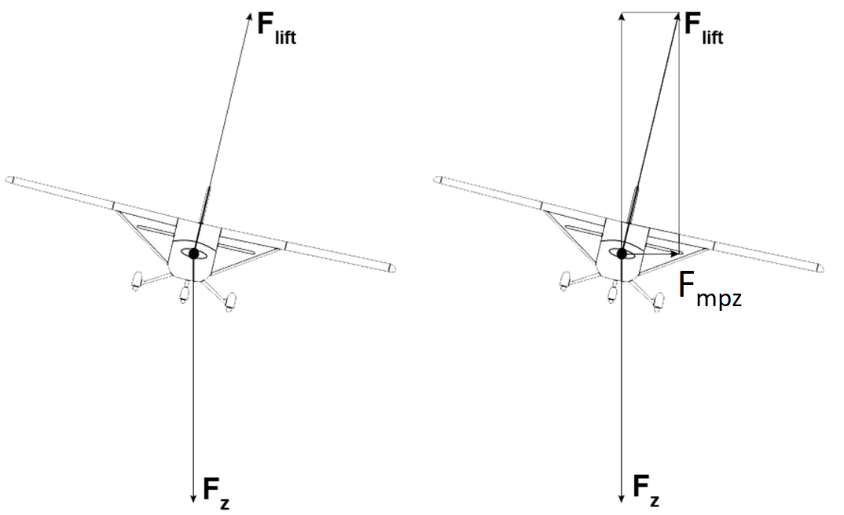
Als een vliegtuig een bocht wil maken, dan moet het vliegtuig zorgen voor een kracht loodrecht op de bewegingsrichting. Dit doet een vliegtuig door te kantelen (zie de onderstaande linker afbeeldingen). Op de vleugels werkt een liftkracht die altijd loodrecht op de vleugels werkt. Door te kantelen krijgt deze liftkracht een component in de horizontale richting (zie de middelste onderstaande afbeelding). Deze horizontale component staat loodrecht op de bewegingsrichting van het vliegtuig en zal dus fungeren als een middelpuntzoekende kracht.
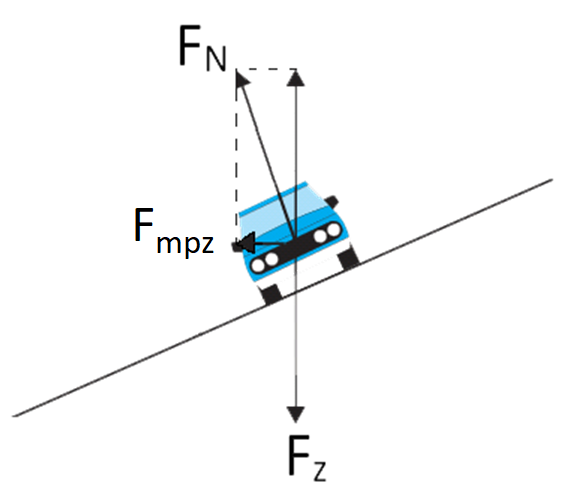
Om het gemakkelijker te maken voor auto's om de bocht door te komen wordt een soortgelijk effect gebruikt. Het wegdek wordt een beetje gekanteld, zodat de normaalkracht van de weg een horizontale component krijgt en kan fungeren als middelpuntzoekende kracht (zie de rechter afbeelding). Zonder deze normaalkracht zou alleen de wrijvingskracht de middelpuntzoekende kracht kunnen leveren en als deze kracht niet voldoende is, dan vliegt de auto uit de bocht.
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§5 Gewichtloosheid (VWO)
In deze paragraaf kijken we nogmaals terug naar het begrip gewicht en gewichtloosheid. Deze keer passen we het toe op de cirkelbeweging.
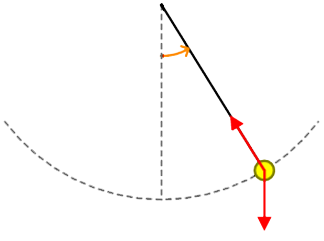
Ook de middelpuntzoekende kracht kan ervoor zorgen dat een persoon gewichtloosheid ervaart. Dit kunnen we begrijpen met het volgende voorbeeld. In de onderstaande afbeelding zien we een aantal achtbaankarretjes door de bocht gaan. Als een karretje stil zou staan boven op deze bocht, dan zou een persoon in dit karretje met zijn volledige zwaartekracht tegen zijn stoel drukken. Als het karretje met een behoorlijke snelheid deze bocht maakt, dan is er een middelpuntzoekende kracht nodig om de persoon in zijn baan te houden. Deze kracht wordt geleverd door de zwaartekracht van de persoon. Een deel van de zwaartekracht van de persoon zal nu dus niet gebruikt worden om de persoon tegen de stoel te drukken, maar zal gebruikt worden als middelpuntzoekende kracht. Als gevolg voelt de persoon zich nu lichter.

Als de kar nog sneller gaat bewegen, dan komt er een moment dat de zwaartekracht gelijk wordt aan de middelpuntzoekende kracht. De volledige zwaartekracht wordt nu dus gebruikt als middelpuntzoekende kracht en er is dus geen kracht meer over waarmee de persoon tegen de stoel drukt. Als gevolg ervaart de persoon nu gewichtloosheid.
Hetzelfde effect vindt plaats in een satelliet in zijn baan om de aarde. We krijgen een satelliet in een baan om de aarde door het een snelheid mee te geven, waarbij de middelpuntzoekende kracht gelijk wordt aan de gravitatiekracht. Als gevolg is de satelliet gewichtloos en valt het niet terug naar de aarde. De satelliet bevindt zich dan in een baan om de aarde.
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
| ||||||||
|
§6 De algemene gravitatiekracht
In deze paragraaf gaan we begrijpen hoe objecten in een baan om een hemellichaam terecht kunnen komen. We zullen ook de benodigde formules opstellen om deze baan te beschrijven.
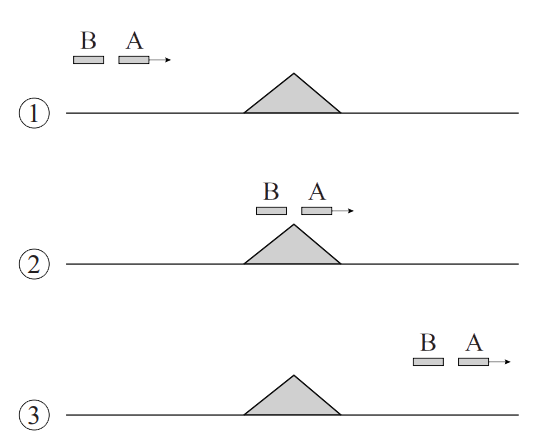
Voor Newton's ontdekkingen, dachten wetenschappers dat de natuurwetten op aarde anders waren dan de natuurwetten in de ruimte. In de ruimte zien we objecten namelijk vaak in cirkelbanen bewegen, terwijl dit op aarde slechts zelden gebeurt. Newton liet echter zien dat met dezelfde formule zowel het vallen van voorwerpen op aarde als de planeetbanen verklaard konden worden. Newton's redenering was als volgt. Stel dat we een gigantisch kanon op aarde zouden bouwen (zie de onderstaande afbeelding en de animatie op de website)(zie de onderstaande animatie). En stel dat we dan een kogel zo snel af schieten dat de valbeweging van de kanonskogel dezelfde bocht maakt als de kromming van de aarde. In dat geval zou de kogel altijd blijven vallen, maar nooit dichter bij de aarde komen. Toen claimde Newton dat de maan ook op deze manier om de aarde beweegt. De beweging van de maan was dus gewoon met de zwaartekracht te verklaren!
Satellieten die wij zelf in een baan om de aarde hebben gebracht, bewegen ook op deze manier. Een goed voorbeeld hiervan is het Internationale Ruimtestation (ISS). Mensen in dit station ervaren gewichtloosheid. Veel mensen denken dat dit komt doordat dit ruimtestation zo ver weg van de aarde staat dat zwaartekracht daar niet meer werkt. Dit is echter onjuist. Het internationale ruimtestation bevindt zich slechts op een hoogte van zo'n 400 km boven het aardoppervlak. Op deze hoogte is de zwaartekracht nog sterk aanwezig. De reden dat personen hier toch gewichtloosheid ervaren, is omdat ze een vrije val maken (zonder dichter bij de aarde te komen). In de eerste paragraaf hebben we geleerd dat een vrije val altijd zorgt voor gewichtloosheid.
Newton begreep ook dat alle voorwerpen in het universum elkaar aantrekken doormiddel van de zwaartekracht (Fz), ook wel de gravitatiekracht (Fg) genoemd. Het woord "zwaartekracht" gebruiken we meestal als we vallende voorwerpen dicht bij het aardoppervlak bespreken. Het woord "gravitatiekracht" gebruiken we voor objecten die in de ruimte bewegen.
In de extra paragraaf op de website zullen we bewijzen dat de gravitatiekracht gegeven wordt door:
$$ F_g = \frac{GMm}{r^2}$$
|
Als we deze formule gelijkstellen aan de al bekende formule "Fz=mg", dan vinden we:
$$ mg = \frac{GMm}{r^2} $$Als we de massa "m" aan beide kanten wegstrepen, dan vinden we dat de valversnelling "g" te berekenen is met:
$$ g = \frac{GM}{r^2} $$
|
Als we hier voor M de massa van de aarde invullen en voor r de straal van de aarde, dan vinden we de bekende waarde 9,81 m/s2 terug.
Als een object een cirkelbaan maakt dankzij de gravitatiekracht, dan geldt:
$$ F_{mpz} = F_g $$ $$\frac{mv^2}{r} = \frac{GMm}{r^2} $$We kunnen hier aan beide kanten een "m" en een "r" wegstrepen en daarna kunnen we de formule herschrijven tot:
$$ v = \sqrt{\frac{GM}{r}} $$
|
 Voorbeeld
Voorbeeld
|
|
Vraag: In BINAS kan je de massa van de aarde opzoeken. Ga met een berekening na dat de waarde uit BINAS klopt. Antwoord: De massa van de aarde komt o.a. voor in de formule uit deze paragraaf met de valversnelling: $$ g = \frac{GM}{r^2} $$Als we deze formule omschrijven en dan voor r de straal van de aarde invullen, dan vinden we: $$ M = \frac{gr^2}{G} $$ $$ M = \frac{9,81 \times (6,371\times 10^6)^2}{6,67430 \times 10^{-11}} = 5,97 \times 10^{24} \text{ kg} $$Dit komt overeen met de waarde van BINAS. Op deze manier kunnen we dus de massa van de aarde berekenen! Vraag: Het internationale ruimtestation (ISS) maakt een baan om de aarde op een hoogte van 400 km boven het aardoppervlak. Bereken de snelheid van het ruimtestation. Antwoord: De afstand (r) van het centrum van de aarde tot de satelliet is in dit geval: $$ r = 6,371 \times 10^6 + 400 \times 10^3 = 6,771 \times 10^6 \text{ m} $$Met de laatste formule uit de theorie kunnen we dan de baansnelheid uitrekenen. Voor M vullen we de massa van de aarde in: $$ v_{baan} = \sqrt{\frac{GM}{r}} $$ $$ v_{baan} = \sqrt{\frac{6,67430 \times 10^{-11} \times 5,972 \times 10^{24}}{6,771 \times 10^6}} = 7,67 \times 10^3 \text{ m/s}$$Met deze snelheid maakt het ruimtestation elke anderhalf uur een rondje om de aarde!
|
 VWO
VWO
| |||||||||
|
Als we de bovenstaande formule voor de baansnelheid (v = √(GM/r)) combineren met "v=2πr/T", dan vinden we: $$ \left( \frac{2\pi r}{T} \right)^2 = \frac{GM}{r}$$Dit kunnen we herschrijven tot:
Deze formule wordt de derde wet van Kepler genoemd.
|
 Voorbeeld (VWO)
Voorbeeld (VWO)
|
|
Vraag: In BINAS is de massa van de zon te vinden. Laat met een berekening zien dat deze massa correct is. Antwoord: We kunnen de massa bepalen door de baan van de aarde om de zon te bestuderen. We weten de afstand van de aarde tot de zon (r = 149,6 × 109 m) en de omlooptijd van de aarde (T = 365,256 dagen). Als we de wet van Kepler omschrijven, dan kunnen we hiermee de massa van de zon uitrekenen: $$ M = \frac{4\pi^2 r^3}{GT^2}$$ $$ M = \frac{4\pi^2 \times (149,6 \times 10^9)^3}{6,67384 \times 10^{-11} \times (365,256 \times 24 \times 60 \times 60)^2} = 1,99 \times 10^{30} \text{ kg}$$ Dit is ook de massa die we in BINAS vinden.
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
 Extra
Extra
|
|
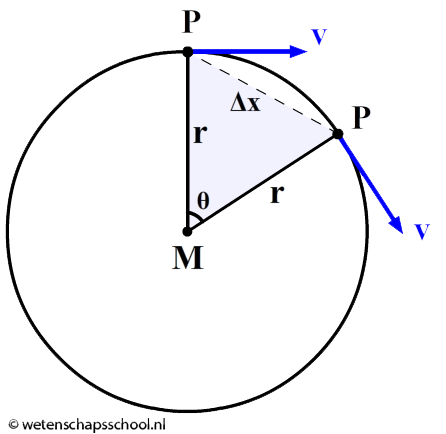
In dit extra stukje stof leiden we de formule voor de middelpuntzoekende kracht af en daarna de formule voor de gravitatiekracht. Als op een voorwerp alleen een middelpuntzoekende kracht werkt, dan geldt volgens de tweede wet van Newton: $$ F_{mpz} = F_{res} = ma $$De middelpuntzoekende kracht zorgt dus voor een versnelling. Maar hadden we niet aangenomen dat de baansnelheid constant is? Hoe kan er hier dan een versnelling zijn? Dit kunnen we goed zien in de onderstaande afbeelding. Als deeltje P in zijn cirkelbaan beweegt, verandert de grootte van de snelheid niet, maar wel de richting. Voor het veranderen van de richting is een versnelling nodig. Deze versnelling wijst naar het middelpunt van de cirkelbeweging en houdt op deze manier het deeltje in zijn baan.
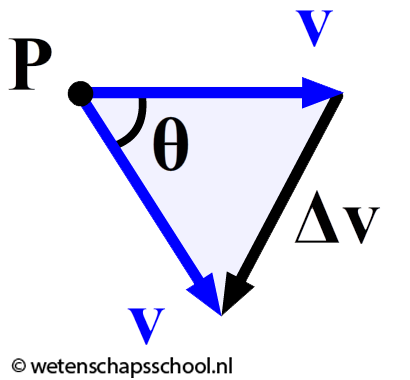
In de onderstaande afbeelding is het draaien van de snelheid weergegeven gezien vanaf het punt P. Zoals gebruikelijk noemen we het verschil tussen de begin- en de eindsnelheid Δv.
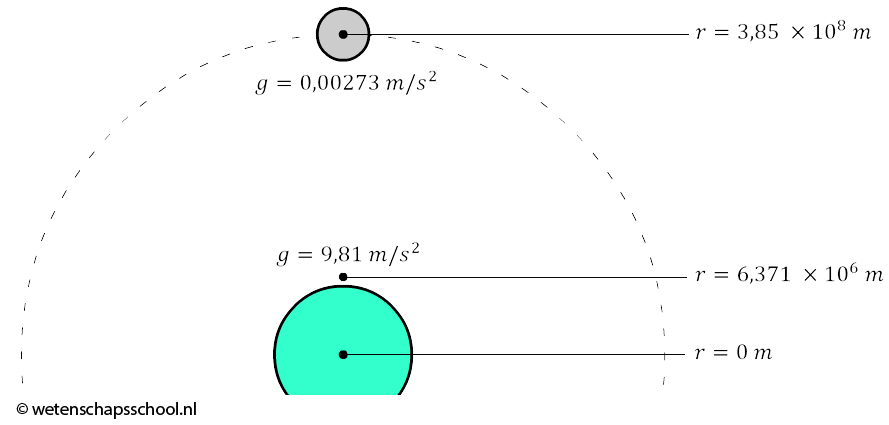
In de vorige twee afbeeldingen zien we twee gelijkbenige driehoeken met dezelfde hoek θ. Deze twee driehoeken hebben dus dezelfde verhoudingen. Er geldt dus: $$ \frac{\Delta x}{r} = \frac{\Delta v}{v} $$Dit kunnen we omschrijven tot: $$ \Delta v = \frac{v \Delta x}{r} $$Als we beide zijden door Δt delen, dan vinden we met behulp van de formule v=Δx/Δt : $$ \frac{\Delta v}{\Delta t} = \frac{v^2}{r}$$Omdat a=Δv/Δt kunnen we dit herschrijven tot: $$ a_{mpz} = \frac{v_{baan}^2}{r}$$We hebben nu gevonden hoe groot de middelpuntzoekende versnelling moet zijn om een deeltje in zijn baan te houden. Deze formule is voor het eerst afgeleid door de nederlandse natuurkundige Christiaan Huygens. Door beide kanten van de formule met de massa te vermenigvuldigen kunnen we gemakkelijk de formule voor de middelpuntzoekende kracht afleiden: $$ F_{mpz} = \frac{mv^2}{r} $$Met deze formule voor de middelpuntzoekende versnelling kunnen we bijvoorbeeld de versnelling van de maan uitrekenen. De maan heeft een omlooptijd van 27,32 dagen (2,36 × 106 s) en de afstand van het centrum van de aarde tot het centrum van de maan is 3,85 × 108 m. De baansnelheid is dus gelijk aan: $$ v_{baan} = \frac{2\pi r}{T} = \frac{2\pi \times 3,85\times 10^8}{2,36\times 10^6} = 1,03 \times 10^3 \text{ m/s} $$Met de baansnelheid kunnen we de versnelling uitrekenen: $$ a_{mpz} = \frac{v_{baan}^2}{r} = \frac{(1,03 \times 10^3)^2}{3,85\times 10^8} = 0,00273 \text{ m/s}^2 $$Dit is de valversnelling die de maan ondergaat! Vanwege de grote afstand van de aarde is dit een stuk kleiner dan de 9,81 m/s2 die we op aarde gewend zijn (zie de onderstaande afbeelding)! De valversnelling is over deze afstand een factor 9,81/0,00273 ≈ 3600 afgenomen.
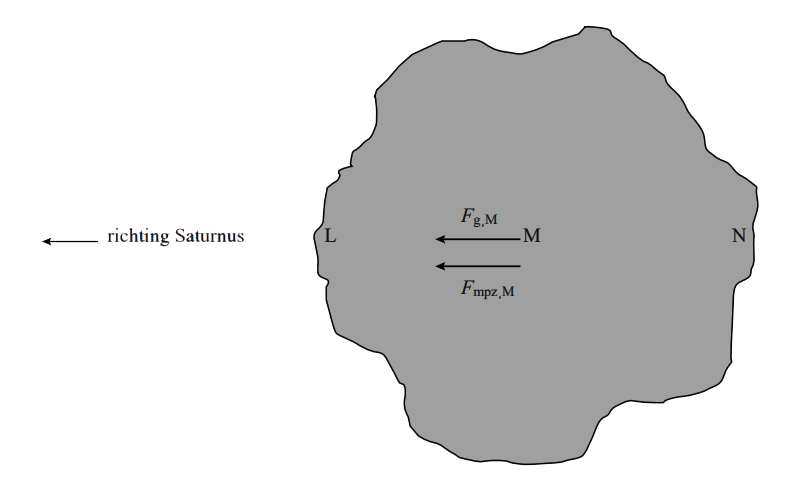
Newton deed voor het eerst onderzoek naar de versnelling van de maan. Hij wist dat de afstand van de aarde tot de maan 60x zo groot was als de straal van de aarde. Over deze afstand was de valversnelling 602 = 3600x afgenomen. We hebben hier dus te maken met een omgekeerd kwadratisch verband. Er geldt dus: $$ g = \frac{\text{constant}}{r^2} $$Door beide kanten met de massa te vermenigvuldigen vinden we de formule voor de gravitatiekracht: $$ F_g = \frac{\text{constant} \times m}{r^2} $$Volgens de derde wet van Newton weten we dat als de aarde aan de maan trekt, dat dan de maan ook aan de aarde moet trekken met een even grote kracht (zie de onderstaande afbeelding). In dat geval is de kracht echter afhankelijk van de massa van de aarde (M): $$ F_g = \frac{\text{constant} \times M}{r^2} $$
Als we deze formules combineren, dan vinden we: $$ F_g = \frac{\text{constant} \times Mm}{r^2} $$De constante wordt nu G genoemd en dit geeft ons de bekende formule voor de gravitatiekracht: $$ F_g = \frac{\text{GMm}}{r^2} $$
|
| BINAS: | |
| 5 | Astronomische eenheid en lichtjaar |
| 7 | Gravitatieconstante |
| 31 | Gegevens over planeten en manen |
| 32B | Gegevens over sterren |
| 32C | Gegevens over de zon |