Hoofdstuk 1
Basisvaardigheden
§1 Natuurkunde §2 Volume en massa §3 Grootheden en eenheden §4 Formules §5 Dichtheid §6 Drijven en zinken
§1 Natuurkunde
In dit hoofdstuk ga je de basisvaardigheden leren waarmee je natuurkunde de rest van het jaar goed kan begrijpen. In deze eerste paragraaf bespreken het verschil tussen natuurkunde, scheikunde en biologie.
Welkom bij de wetenschapsschool. Op deze website ga je leren over de wetenschap genaamd natuurkunde. Het doel van wetenschap is te begrijpen hoe de wereld werkt. Natuurkunde is echter niet de enige wetenschap. Naast de natuurkunde bestaat ook o.a. de scheikunde en de biologie. In de rest van deze paragraaf bespreken we de verschillen.
De scheikunde gaat over stoffen. In dit vak bestuderen we de eigenschappen van deze stoffen en onderzoeken we waar deze stoffen uit opgebouwd zijn. In sommige omstandigheden veranderen stoffen in compleet andere stoffen. Als dit gebeurt, spreken we van een chemische reactie. Tijdens een chemische reactie kan er van alles gebeuren. Stoffen kunnen van kleur veranderen, licht geven of zelfs ontploffen. Hieronder zien we links bijvoorbeeld een wit poeder genaamd kopersulfaat dat blauw wordt als het in contact komt met water. Rechts zien we de verbranding van thermiet dat o.a. gebruikt wordt voor het lassen van tramrails.
 (Afbeelding: Benjah-bmm27; PD / CaesiumFluoride; CC BY-SA 3.0)
(Afbeelding: Benjah-bmm27; PD / CaesiumFluoride; CC BY-SA 3.0)
 EXPERIMENT
EXPERIMENT
| ||
|
Natuurkunde gaat over de natuurwetten die in het universum werken. Deze wetten beschrijven hoe materie beweegt onder invloed van verschillende Krachten. Twee belangrijke begrippen in de natuurkunde zijn dus beweging en Kracht. Bij beweging kan je bijvoorbeeld denken aan het opstijgen van een vliegtuig of het vallen van een steen. Ook de onderwerpen geluid, Warmte, en licht behoren bij de natuurkunde. Deze fenomenen worden namelijk veroorzaakt door de bewegingen van vele miljarden kleine deeltjes. De bekendste Kracht is de zwaarteKracht. Andere bekende Krachten zijn de elektrische en de magnetische Kracht.
Hieronder zijn een aantal onderwerpen uit de natuurkunde afgebeeld. We zien een parachutesprong (zwaarteKracht), ledlampen (licht), bliksem (Elektriciteit), een foto genomen met een infraroodcamera (Warmte), de trillingen van een gitaarsnaar (geluid) en een magneet waarmee ijzervijlsel wordt aangetrokken (magnetisme).
 (Afbeelding: Krzysztof Wilk PD / Gerlos CC BY-SA 2.0 / Tyler Nienhouse CC BY-SA 2.0 / Alex and Jarek Tuszynski CC BY-SA 3.0 / ... / Oguraclutch CC BY-SA 3.0)
(Afbeelding: Krzysztof Wilk PD / Gerlos CC BY-SA 2.0 / Tyler Nienhouse CC BY-SA 2.0 / Alex and Jarek Tuszynski CC BY-SA 3.0 / ... / Oguraclutch CC BY-SA 3.0)
Hoewel natuurkunde het woord "natuur" bevat, heeft het weinig te maken met het leven op aarde. Dit onderwerp wordt beschreven door de biologie.

 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§2 Volume en massa
In de natuurkunde proberen we de wereld te begrijpen door metingen te doen. Twee van de belangrijkste eigenschappen die we kunnen meten zijn de massa (hoe zwaar iets is) en het volume (hoeveel ruimte iets inneemt). In deze paragraaf bespreken we de verschillende maten waarin deze eigenschappen worden gemeten.
Om de wereld te kunnen beschrijven, is het belangrijk dat we kunnen meten hoe groot voorwerpen zijn. We gebruiken hiervoor de lengte, de oppervlakte en het volume. De lengte meten we meestal in:

De oppervlakte meten we meestal in:
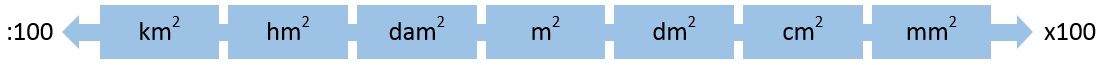
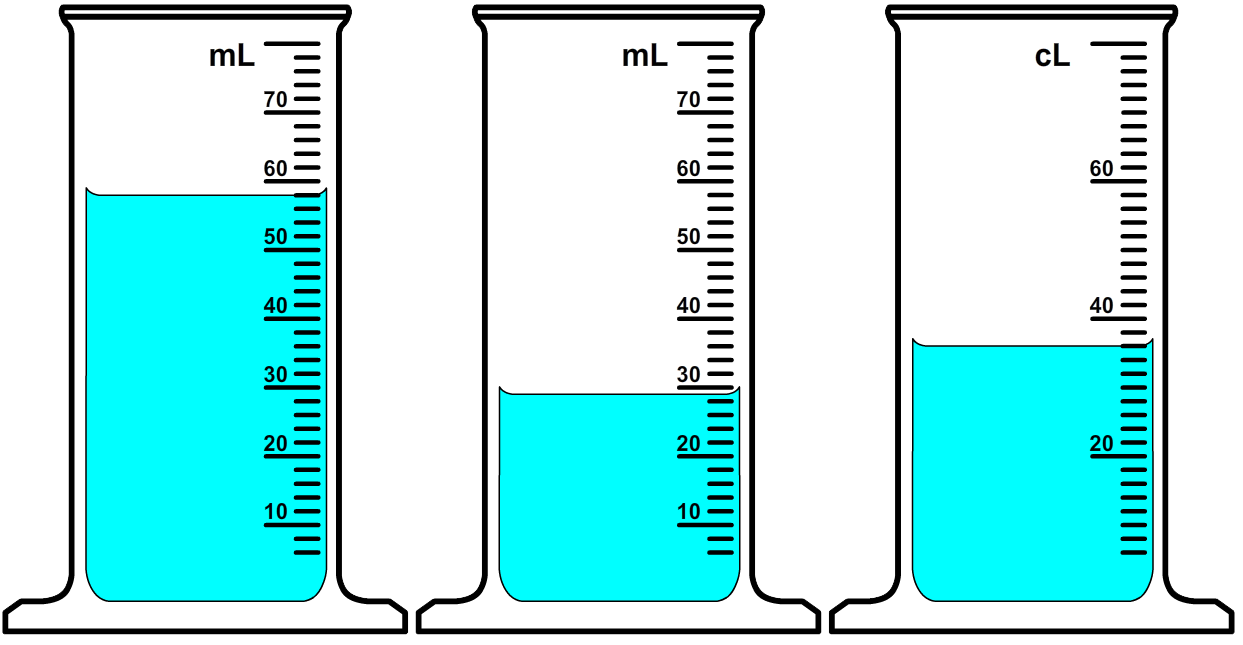
Het volume kunnen we zowel in kubieke meter (m3) als liter (L) meten. Er geldt:
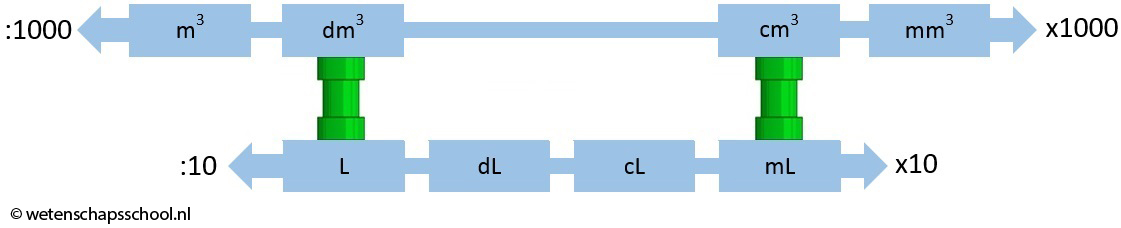
Zoals je in de afbeelding kan zien is 1 L exact hetzelfde als 1 dm3. Ook geldt dat 1 mL hetzelfde is als 1 cm3:
| $$ 1 \text{ L} = 1 \text{ dm}^3 \;\;\;\;\;\;\;\;\; 1 \text{ mL} = 1 \text{ cm}^3 $$ |
 Voorbeelden
Voorbeelden
|
|
Vraag: Reken 3,5 kubieke decimeter om naar kubieke millimeter. Antwoord: Van kubieke decimeter (dm3) naar kubieke millimeter (mm3) moeten we in de onderstaande afbeelding twee stappen naar rechts doen. We doen dus twee maal keer 1000: $$ 3,5 \times 1000 \times 1000 = 3\; 500\; 000 \text{ mm}^3 $$ 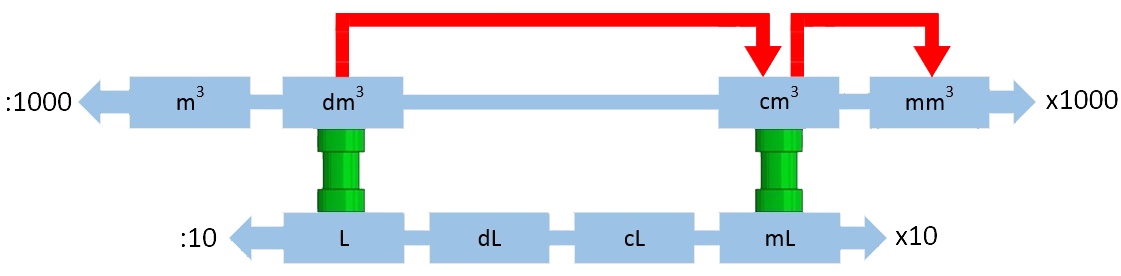
|
 Voorbeelden
Voorbeelden
|
|
Vraag: Een voorwerp heeft een volume van 0,035 milliliter. Geef het volume in kubieke millimeter. Antwoord: Milliliter (mL) is gelijk aan kubieke centimeter (cm3). Er geldt dus: $$ 0,035 \text{ mL} = 0,035 \text{ cm}^3 $$ Dan gaan we van kubieke centimeter (cm3) naar kubieke millimeter (mm3). In dat geval moeten we in de onderstaande afbeelding één stap naar rechts doen. We doen dus één maal keer 1000: $$ 0,035 \times 1000 = 35 \text{ mm}^3 $$ 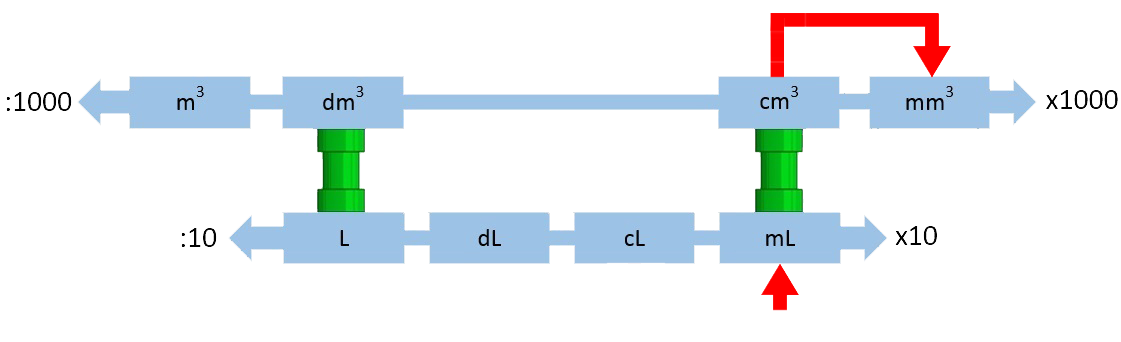
|
Als een voorwerp de vorm heeft van een balk (zie de rechter afbeelding), dan kunnen we het volume van dit voorwerp met de volgende formule berekenen:
$$\text{volume } = \text{ lengte } \times \text{ breedte } \times \text{ hoogte }$$Dit korten we meestal af tot:
$$ V = l \times b \times h $$
|

Laten we dit toepassen op de balk die rechts is afgebeeld. We zien een lengte van 5,0 m, een breedte van 2,0 m en een hoogte van 1,5 m. We vinden:
$$ V = l \times b \times h $$ $$ V = 5,0 \times 2,0 \times 1,5 = 15 \text{ m}^3$$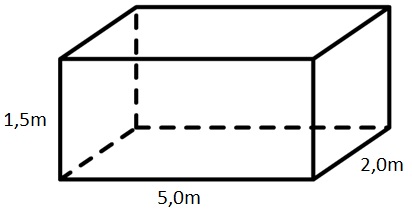
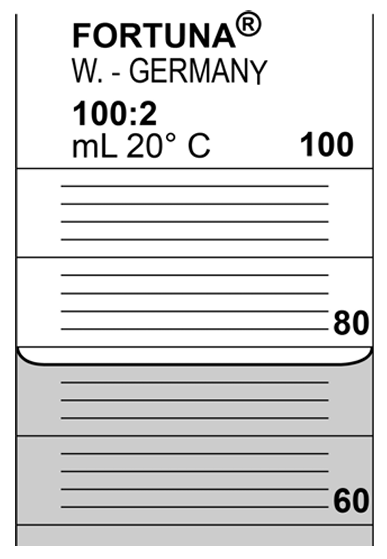
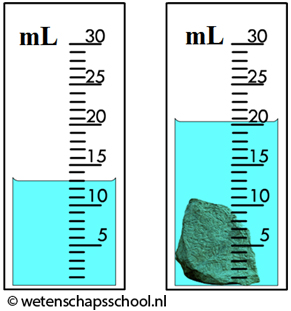
Als een voorwerp een ingewikkelde vorm heeft, dan kunnen we het volume vaak niet met een formule bepalen. In dat geval gebruiken we een slim experiment genaamd de onderdompelmethode. Stel we willen het volume van een steentje bepalen, dan kunnen we het steentje in een maatcilinder met water doen en kijken hoeveel het water stijgt. In het onderstaande voorbeeld is het water bijvoorbeeld gestegen van 15 naar 24 mL. Het water is dus 24 - 15 = 9 mL gestegen en het volume van de steen is dus ook 9 mL.
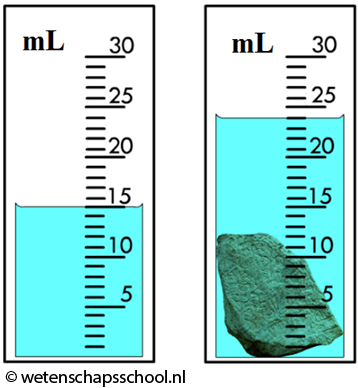
Merk op dat aan de wanden van de maatcilinder het water iets omhoogtrekt. Dit is in de afbeelding rechtsboven duidelijk te zien. Voor het aflezen van de maatcilinder kijk je altijd naar de stand van de vloeistof in het midden. In dit geval lezen we de maatcilinder af op 21,7 mL (ga dit zelf na!).
 (Afbeelding: PRHaney; CC BY-SA 3.0)
(Afbeelding: PRHaney; CC BY-SA 3.0)
Om de wereld te kunnen beschrijven, is het ook belangrijk dat we kunnen meten hoe zwaar voorwerpen zijn. Hiervoor wordt het begrip massa gebruikt. In het dagelijks leven wordt voor de massa ook wel het woord "gewicht" gebruikt. Dit is echter onjuist. In klas 4 zullen we het verschil tussen massa en gewicht toelichten. Voor de massa gebruiken we dezelfde voorvoegsels als bij de lengte:

Normaal gesproken gebruiken we echter alleen de milligram, de gram en de kilogram:

In het dagelijks leven wordt voor de massa ook wel het woord "gewicht" gebruikt. Dit is echter onjuist. In klas 4 zullen we het verschil tussen massa en gewicht toelichten.
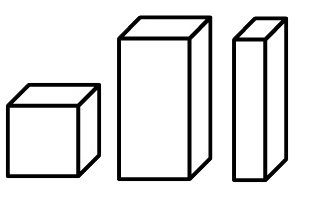
Het is belangrijk om het begrip volume en het begrip massa goed uit elkaar te houden. Het volume beschrijft hoeveel ruimte een voorwerp inneemt. De massa beschrijft hoe zwaar een voorwerp is. In de rechter afbeelding wordt het verschil duidelijk. We zien een groot stuk piepschuim en een kleine ijzeren kogel. Het stuk piepschuim heeft een groter volume, omdat het meer ruimte inneemt. De kogel heeft een grotere massa, omdat het zwaarder is.

 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
| ||||||||
|
§3 Grootheden en eenheden
In deze paragraaf bespreken we het verschil tussen de eigenschappen die we kunnen meten (grootheden) en de maten waarin we deze eigenschappen meten (eenheden). Ook bespreken we de zogenaamde SI-eenheden.
In de wetenschap beschrijven we de wereld door metingen te verrichten. Alle eigenschappen die we kunnen meten noemen we grootheden. Voorbeelden van grootheden zijn lengte, oppervlakte, volume, tijd, temperatuur en snelheid. De maten waarin we deze eigenschappen meten worden eenheden genoemd. Voorbeelden van eenheden zijn meter, vierkante meter, kubieke meter, seconde, minuut, graden Celsius en meter per seconde.
Hieronder staan een aantal belangrijke grootheden en eenheden samengevat:
| Grootheden | Eenheden |
| Lengte | meter (m)centimeter (cm) |
| Oppervlakte | vierkante meter (m2)vierkante centimeter (cm2) |
| Volume | kubieke meter (m3)kubieke centimeter (cm3)liter (L) |
| Massa | kilogram (kg)gram (g) |
| Tijd | seconden (s)minuten (min)uren (h) |
| Temperatuur | graden Celsius (oC)kelvin (K) |
| Snelheid | meter per seconde (m/s)kilometer per uur (km/h) |
Een eenheid is gemakkelijk te herkennen doordat we het achter een getal kunnen plaatsen. We zeggen bijvoorbeeld 25 meter, maar niet 25 lengte. Meter is dus een eenheid en lengte niet. In het vak natuurkunde is het verplicht om bij het eindantwoord van een berekening altijd de eenheid te noteren.
Een aantal eenheden zijn in het verleden uitgeroepen tot standaardeenheden. We noemen dit ook wel de SI-eenheden (SI is een afkorting van "Système international d'unités", oftewel "standaard internationale eenheden"). De meest fundamentele SI-eenheden worden de SI-grondeenheden genoemd. Een aantal hiervan staan hieronder in de tabel:
| Grootheid | SI-grondeenheid |
| Afstand | meter (m) |
| Tijd | seconde (s) |
| Massa | kilogram (kg) |
| Temperatuur | kelvin (K) |
Door de SI-grondeenheden te combineren kunnen we andere SI-eenheden afleiden. Van de SI-grondeenheid meter (m) kunnen we bijvoorbeeld de SI-eenheid vierkante meter (m2) en kubieke meter (m3) maken. Met meter (m) en seconde (s) kunnen we bijvoorbeeld de SI-eenheid meter per seconde (m/s) maken. We noemen dit afgeleide SI-eenheden.
In de natuurkunde zal je regelmatig worden gevraagd om een bepaalde meetwaarde om te rekenen naar SI-eenheden. Hieronder zien we hiervan twee voorbeelden:
 Voorbeeld
Voorbeeld
|
|
Vraag: Reken 500 g om in SI-eenheden. Antwoord: De SI-eenheid van de massa is kilogram. Omgerekend wordt dit 0,500 kg. Vraag: Reken 20 L om in SI-eenheden. Antwoord: De SI-eenheid van het volume is de kubieke meter. We gaan liter dus omschrijven naar kubieke meter. Omgerekend wordt dit 20 L = 20 dm3 = 0,020 m3.
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§4 Formules
Processen in de natuurkunde worden vaak beschreven met formules. In deze paragraaf gaan we leren hoe we deze formules kunnen omschrijven in verschillende vormen. In de volgende paragraaf gaan we deze techniek meteen toepassen.
Stel een auto legt een bepaalde afstand af in een bepaalde tijd. De snelheid van de auto kan dan worden berekend met:
$$ \text{snelheid} = \frac{\text{afstand}}{\text{tijd}} $$Dit korten we meestal af met de volgende letters:
$$ v = \frac{\Delta x}{\Delta t} $$
|
Als een auto bijvoorbeeld 300 meter aflegt in 25 seconde, dan is de snelheid van de auto gelijk aan:
$$ v = \frac{300}{25} = 12 \text{ m/s}$$Als we de formule willen gebruiken om niet de snelheid, maar juist de verplaatsing of de tijdsduur uit te rekenen, dan moeten we deze formule leren omschrijven. Om dit te doen hebben we een wiskundig trucje nodig. Als in een vergelijking aan de ene kant van de "=" wordt gedeeld door een bepaald getal, dan kan je in plaats daarvan ook de andere kant van de "=" vermenigvuldigen met ditzelfde getal. Hieronder zien we een getallenvoorbeeld waar dit wordt uitgevoerd:
$$ \frac{6}{3} = 2 $$ $$ \downarrow $$ $$ 6 = 2 \times 3 $$De omgekeerde regel geldt ook. Als we aan de ene kant van de "=" met een waarde vermenigvuldigen, dan kunnen we ook aan de andere kant door deze waarde delen. Dit zien we hieronder:
$$ 6 = 2 \times 3 $$ $$ \downarrow $$ $$ \frac{6}{3} = 2 $$We kunnen dit trucje gebruiken om formules om te schrijven in elke gewenste vorm. Dit doen we in twee stappen. Eerst zorg je dat je een eventuele breuk in de formule wegwerkt. Daarna schrijf je de formule om met het wiskundige trucje dat hierboven beschreven is. Laten we dit toepassen op de formule voor de snelheid. Stel we willen de formule omschrijven zodat we de tijdsduur uit kunnen rekenen. We voeren dan de volgende stappen uit:
$$ v = \frac{\Delta x}{\Delta t} $$ $$ \downarrow $$ $$ v \times \Delta t = \Delta x $$ $$ \downarrow $$ $$ \Delta t = \frac{\Delta x}{v} $$In de eerste stap hebben we "gedeeld door Δt" aan de rechterkant weggehaald en "keer Δt" aan de linkerzijde erbij geschreven. In de tweede stap hebben we "keer v" aan de linkerzijde weggehaald en "gedeeld door v" aan de rechterzijde toegevoegd. We hebben nu de formule voor Δt gevonden. Mocht je deze uitleg wat lastig kunnen volgen, dan raad ik het onderstaande filmpje aan. Deze techniek is namelijk gemakkelijker met in een filmpje uit te leggen.
Met het onderstaande programma kan je oefenen met omschrijven. Merk ook op in welke problemen je komt als je niet eerst de breuk wegwerkt.
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§5 Dichtheid
In deze paragraaf introduceren we het belangrijke begrip dichtheid. Met de dichtheid kunnen we beschrijven dat sommige stoffen zwaarder zijn dan andere.
Niet alle stoffen zijn even zwaar. Een kubieke centimeter goud is zwaarder dan een kubieke centimeter hout (zie de twee linker onderstaande afbeeldingen) en een kubieke centimeter ijzer is zwaarder dan een kubieke centimeter piepschuim (zie de rechter twee afbeeldingen). We beschrijven deze verschillen met het begrip dichtheid.

Een kubieke centimeter ijzer heeft bijvoorbeeld altijd een massa van 7,8 gram. We zeggen daarom dat de dichtheid van ijzer gelijk is aan 7,8 gram per kubieke centimeter. Dit korten we ook wel af tot 7,8 g/cm3. De dichtheid van piepschuim is slechts 0,040 g/cm3. De dichtheid van piepschuim is dus inderdaad veel lager dan de dichtheid van ijzer. Als we in het dagelijks leven zeggen dat ijzer "zwaarder" is dan piepschuim, dan bedoelen we dus eigenlijk dat de dichtheid van ijzer groter is dan dat van piepschuim.
Hieronder zien we links een blokje hout met een massa van 10 gram en een volume van 8,0 cm3. Om de dichtheid van dit hout te bepalen, willen we de massa van 1 cm3 hout te weten komen. De dichtheid is in dit geval dus gelijk aan:
$$ \frac{10}{8,0} = 1,3 \text{ g/cm}^3 $$
Om deze dichtheid te berekenen, hebben we de massa van het blokje gedeeld door het volume. Er geldt dus:
$$ \text{dichtheid} = \frac{\text{massa}}{\text{volume}}$$Dit korten we meestal af tot:
$$\rho = \frac{m}{V}$$
|
In SI-eenheden wordt de dichtheid gegeven in kg/m3, maar er wordt ook regelmatig gebruik gemaakt van g/cm3. In dat geval wordt de massa gegeven in gram en het volume in kubieke centimeter.
Hieronder zie je een tabel met de dichtheden van een aantal stoffen. Je vindt een uitgebreidere versie van deze tabel terug achter in het boek. Je vindt een uitgebreidere versie van deze tabel in het tabellenboek op de website. Let er op dat boven aan de tabel een factor 103 staat. Dit betekent dat je de waarden uit de tabel keer 1000 moet doen.
|
Stof |
Dichtheid (× 103 kg/m3) |
|
Koper |
8,96 |
|
IJzer |
7,87 |
|
Lood |
11,3 |
|
aluminium |
2,70 |
|
Kwik |
13,534 |
|
Goud |
19,3 |
|
vloeibaar water |
0,9982 |
|
IJs |
0,917 |
|
vurenhout |
0,58 |
|
Glas |
2,5-2,6 |
|
Lucht |
1,293 kg/m3 |
 Stappenplan dichtheid
Stappenplan dichtheid
|
|
Vraag: Een leerling vindt een muntstuk met een volume van 1,554 cm3 en een massa van 30 gram. Laat met een berekening zien waar het muntstuk van gemaakt is.
Antwoord: Gegevens (G) Stap 1: Schrijf de gegevens uit de vraag op: m = 30 g V = 1,554 cm3 ρ = ... kg/m3 Stap 2: Omschrijven (O) Schrijf de gegevens zo nodig om naar kilogram en kubieke meter: m = 30 / 1000 = 0,030 kg V = 1,554 / 1000 / 1000 = 0,000001554 m3 Stap 3: Formule (F) Noteer de formule in de juiste vorm. In dit geval willen we de dichtheid (ρ) weten: $$ \rho = \frac{m}{V}$$Stap 4: Invullen en Rekenen (IR) Vul de formule in: $$ \rho = \frac{0,030}{0,000001554} = 19300 \text{ kg/m}^3 $$Stap 5: Eenheid (E) Check of de eenheid achter het antwoord staat. In dit geval kg/m3 Stap 6: Conclusie (C) Zoek in BINAS (of de tabel achter in het boek) op welke stof bij deze dichtheid hoort. Bij 19300 kg/m3 hoort de stof goud.
|
 Stappenplan dichtheid
Stappenplan dichtheid
|
|
Vraag: Bereken de massa van 1,2 dm3 ijzer. Stap 1: Gegevens (G) Schrijf de gegevens uit de vraag op en zoek de dichtheid op: V = 1,2 dm3 ρ = 7870 kg/m3 m = ... kg Stap 2: Omschrijven (O) Schrijf de gegevens om in SI-eenheden. In dit geval moeten we het volume omrekenen naar kubieke meter: V = 0,0012 m3 Stap 3: Formule (F) Schrijf de formule ρ = m/V om in de juiste vorm. Doe dit met de techniek uit de vorige paragraaf (er zijn elk jaar leerlingen die de formule omschrijven door te "gokken". Doe dit niet! Leer in plaats daarvan de techniek uit de vorige paragraaf aan. Hier heb je de rest van het jaar profijt van). In dit geval willen we de massa (m) berekenen. De formule wordt in dat geval: $$ \rho = \frac{m}{V} \;\;\; \rightarrow \;\;\; m = \rho \times V $$Stap 4: Invullen en Rekenen (IR) Vul de formule in: $$ m = 0,0012 \times 7870 = 9,4 \text{ kg} $$Stap 4: Eenheid (E) Check of de eenheid achter het antwoord staat. In dit geval kg.
|
 Experiment
Experiment
| ||
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
| ||||||||||||
|
§6 Drijven of zinken
In deze paragraaf gaan we met de dichtheid uitrekenen of voorwerpen drijven of zinken.
Met de dichtheid kunnen we o.a. voorspellen of een voorwerp zal drijven of zinken. Als een voorwerp een grotere dichtheid heeft dan de omringende vloeistof, dan zal het voorwerp zinken. Als het een lagere dichtheid heeft, dan blijft het drijven.
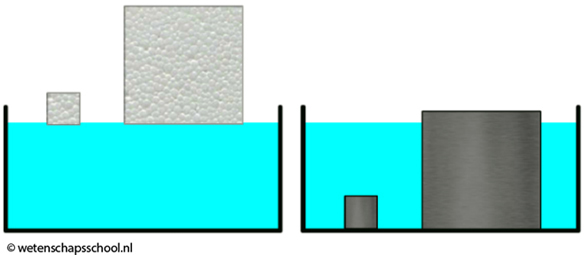
Piepschuim heeft bijvoorbeeld een lagere dichtheid dan water en blijft dus drijven. Dit geldt zelfs als je een gigantisch stuk piepschuim van duizenden kilogram in het water zou leggen (zie de linker afbeelding). Het omgekeerde is waar voor een stukje ijzer. IJzer heeft een grotere dichtheid en als gevolg daarvan zal zelfs het lichtste stukje ijzer zinken (zie de rechter afbeelding).
 Experiment
Experiment
|
| In het eerste onderstaande filmpje zie je drie lagen vloeistof die door verschillende dichtheid op elkaar drijven. Dan worden voorwerpen toegevoegd die drijven op de verschillende lagen. In het tweede filmpje zien we een aluminium bootje dat drijft op een gas met een grote dichtheid. |
 Voorbeeld
Voorbeeld
|
|
Vraag: Een blikje cola heeft een massa van 384 gram en een volume van 380 cm3. Een blikje cola light heeft een massa van 370 gram en hetzelfde volume. Ga met een berekening na of de blikjes drijven of zinken. Antwoord: Voor het blikje cola geldt: m = 384 / 1000 = 0,384 kg V = 380 / 1000 / 1000 = 0,000380 m3 De dichtheid berekenen we als volgt: $$ \rho = \frac{m}{V}$$ $$ \rho = \frac{0,384}{0,000380} = 1011 \text{ kg/m}^3 $$Voor het blikje cola-light geldt: m = 370 g = 0,370 kg V = 380 / 1000 / 1000 = 0,000380 m3 De dichtheid berekenen we als volgt: $$ \rho = \frac{m}{V}$$ $$ \rho = \frac{0,370}{0,000380} = 974 \text{ kg/m}^3 $$In BINAS (of de tabel achter in het boek) zien we dat de dichtheid van water gelijk is aan 998 kg/m3. Het blikje cola heeft een grotere dichtheid
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
| BINAS: | |
| 2 | Voorvoegsels |
| 3-5 | Grootheden en eenheden |
| 8-12 | Dichtheid |
| 31 | Eigenschappen planeten |
| 36 | Volumes en oppervlaktes |
| 35 | Formules |