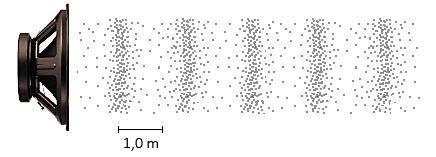Hoofdstuk 3
Geluid
§1 Geluid §2 Trillingstijd en frequentie §3 Golven
§1 Geluid
In dit hoofdstuk gaan we trillingen en golven bestuderen. Hiermee kunnen we o.a. geluid begrijpen. In deze paragraaf bestuderen we het verschil tussen trillingen en golven.
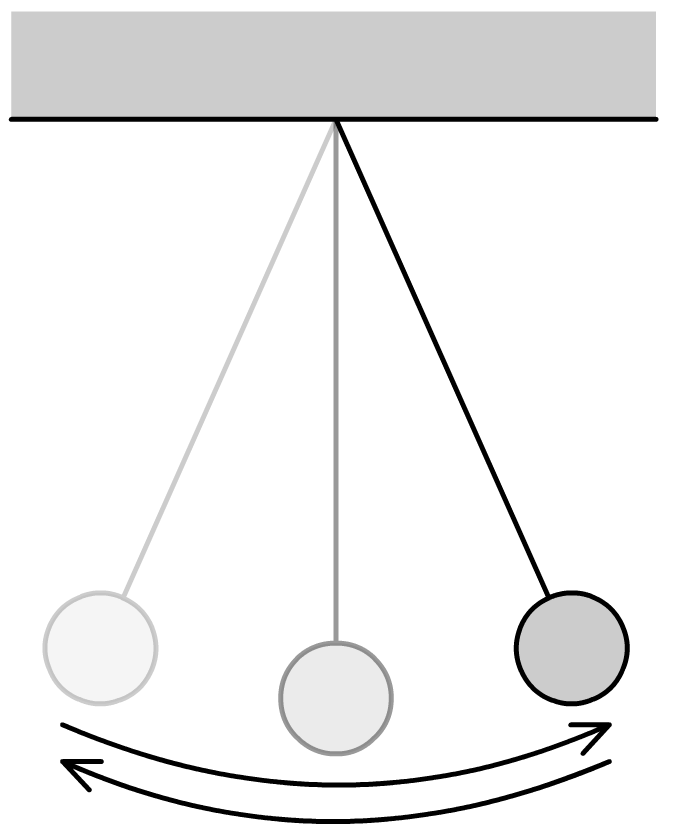
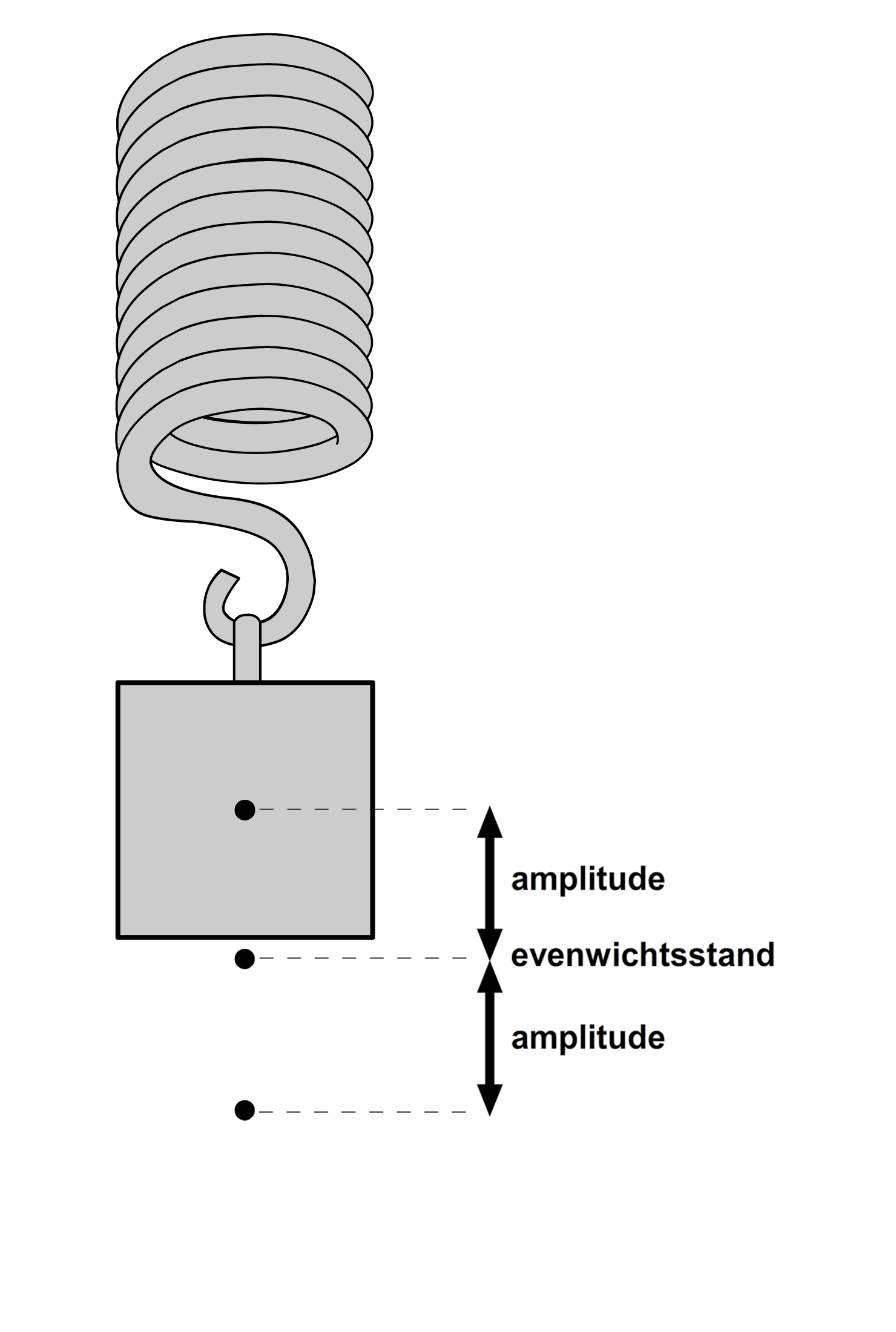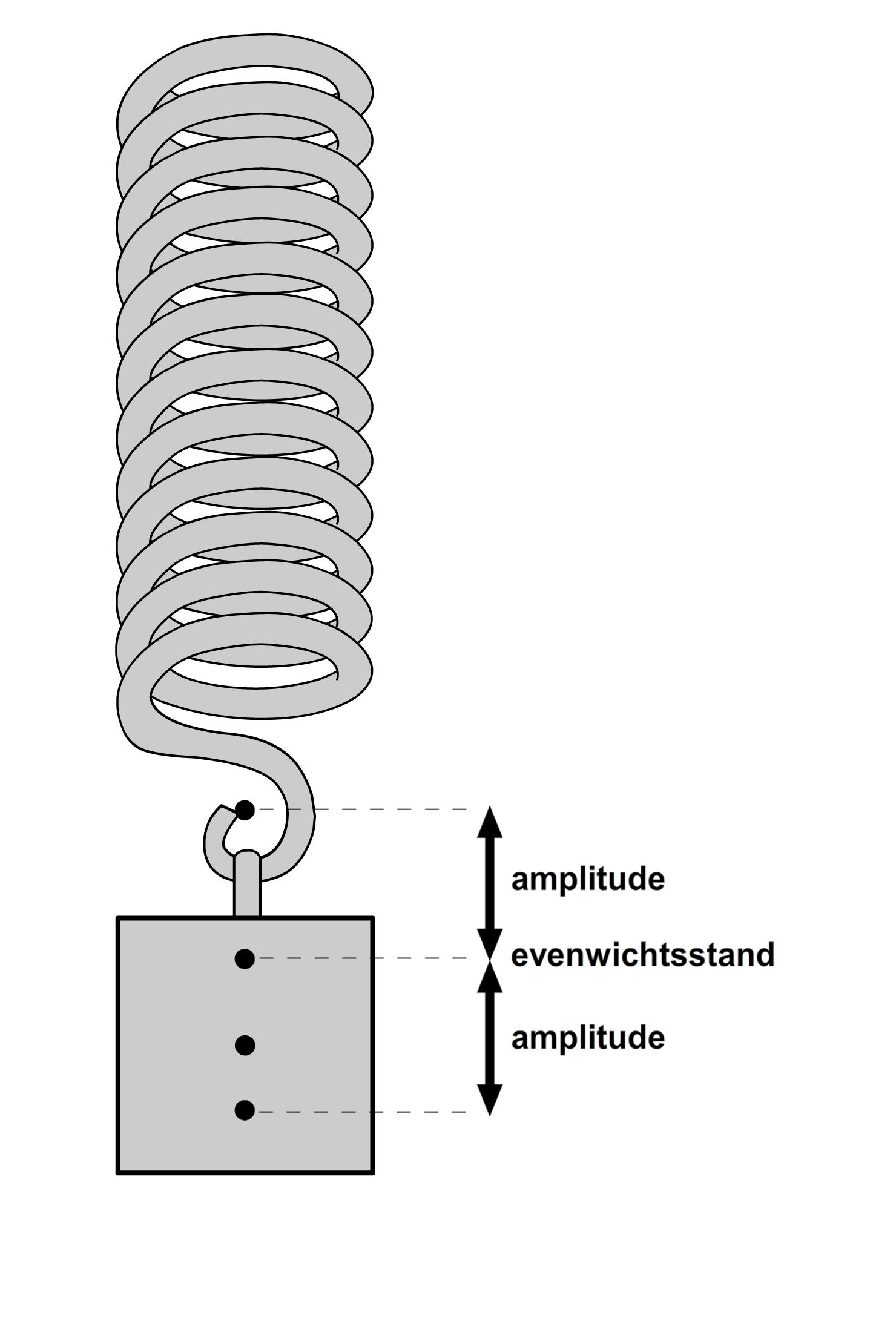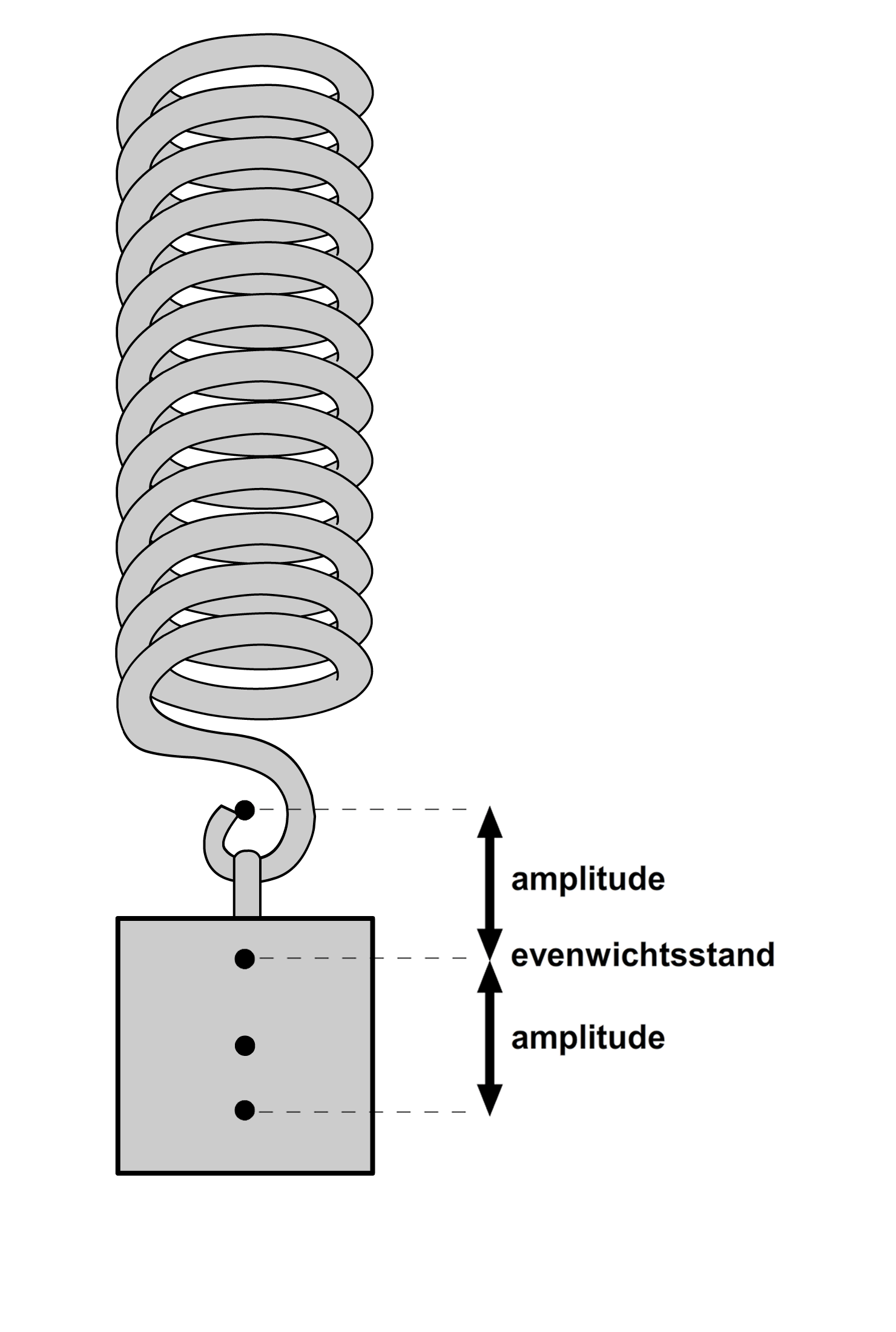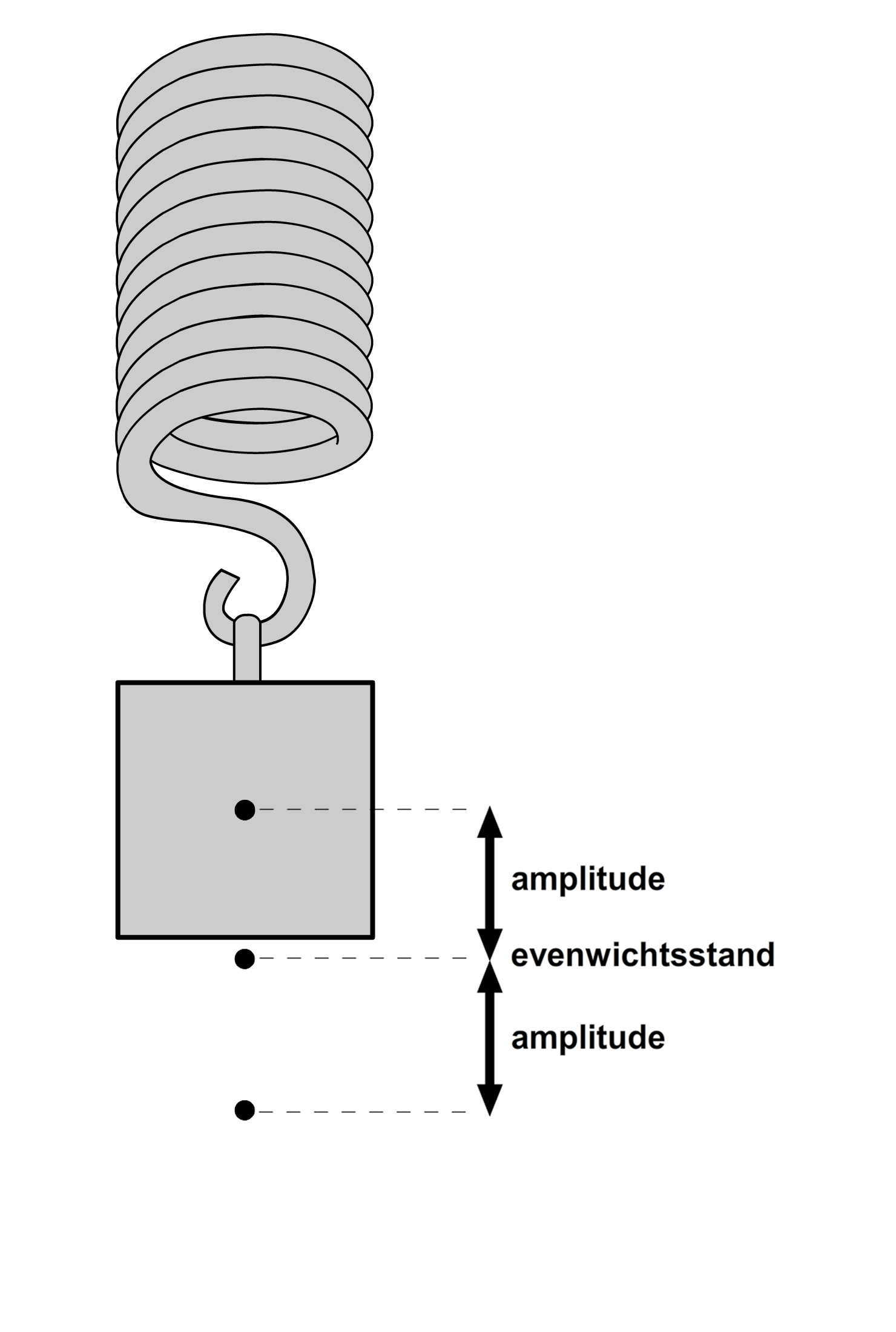
Een trilling is het simpel heen en weer bewegen van een voorwerp. Hieronder zien we twee voorbeelden. Links zien we een slinger (een balletje aan een touwtje) dat heen en weer beweegt. Rechts zien we een blokje dat op en neer beweegt aan een veer (zie ook de onderstaande animatie).
Een ander voorbeeld is het zogenaamde massa-veersysteem. Dit systeem bestaat uit een blokje dat met behulp van een veer heen en weer beweegt over een wrijvingsloos horizontaal oppervlak (zie de onderstaande afbeelding)(zie de onderstaande animatie).
Zoals je kunt zien, beweegt het blokje heen en weer om het punt u = 0 m. We noemen deze positie de evenwichtsstand. Als het blokje hier bevindt, dan bevindt de veer zich in zijn neutrale positie. Rechts van dit punt is de veer uitgerekt. Links van dit punt is de veer ingedrukt. De afstand van het midden van het blokje tot deze evenwichtstand noemen we de uitwijking (u). De maximale uitwijking van het blokje tijdens de trilling noemen we de amplitude (A).
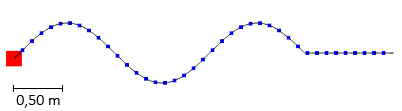
Hieronder is een animatie van een golf te zien. Hieronder zien we een afbeelding van een golf. Op de website, kan je een animatie zien van het ontstaan van deze golf. Door het touw aan de linkerkant op en neer te bewegen, komt het hele touw in beweging. Elk stukje van het touw brengt het volgende stukje in beweging. We noemen de resulterende beweging een golf. Omdat de golf zich naar rechts verplaatst door het touw spreken we van een lopende golf.
Hoewel de golf zelf naar rechts beweegt, doen de deeltjes waaruit het touw bestaat dit niet. In de animatie kan je goed zien dat de deeltjes alleen op en neer bewegen. Elk deeltje voert dus een trilling uit die loodrecht staat op de beweging van de golf. Dit type golf wordt een transversale golf genoemd.
Net als in een touw, kunnen ook in de lucht golven ontstaan. Dit worden geluidsgolven genoemd. Deze golven ontstaan als we een voorwerp in de lucht in trilling brengen. Dit gebeurt bijvoorbeeld bij het trillen van de conus van een speaker, het trillen van een gitaarsnaar of het trillen van stembanden.
In de onderstaande animatie zien we hoe geluidsgolven ontstaan. Op de website kan je ook een animatie van geluidsgolven zien. Het trillende voorwerp (links) botst tegen de omliggende luchtdeeltjes en deze luchtdeeltjes botsen weer tegen de volgende deeltjes etc. De beweging van de luchtdeeltjes zorgt ervoor dat er gebieden ontstaan met een hoge dichtheid (veel deeltjes) en met een lage dichtheid (weinig deeltjes). Deze gebieden van hoge en lage dichtheid vormen een golf die naar rechts beweegt. Het trommelvlies in ons oor kan in trilling worden gebracht door deze golf en zo nemen we geluid waar.
Als je de deeltjes in de animatie volgt, dan zie je dat alle deeltjes naar links en naar rechts bewegen om een evenwichtsstand. Elk deeltje voert dus een trilling uit. De beweging van al deze deeltjes samen zorgt voor een lopende golf die naar rechts beweegt. De deeltjes bewegen in dit geval evenwijdig aan de richting van de golf. We noemen dit longitudinale golven.
Geluidsgolven komen niet alleen in lucht voor. In elk materiaal kunnen geluidsgolven ontstaan. In metalen, bijvoorbeeld, kunnen geluidsgolven zelfs nog sneller voortplanten dan in de lucht. De stof waarin de geluidsgolven zich verplaatsen noemen we het medium. Als een ruimte geen medium bevat, dan spreken we van een vacuüm. In een vacuümruimte kan geluid niet voortplanten. Dit wordt in het volgende filmpje gedemonsteerd.
EXPERIMENT
| ||
|
|
Leerdoelen:
|
|
|
Opdrachten
|
|
§2 Trillingstijd en frequentie
In deze paragraaf gaan we een aantal eigenschappen van trillingen bestuderen, waaronder de trillingstijd en de frequentie.
In de vorige paragraaf hebben we gelezen dat geluid wordt veroorzaakt door het trillen van luchtdeeltjes. We kunnen deze trillingen zichtbaar maken met een oscilloscoop. In de onderstaande afbeelding zien we rechts een oscilloscoop. Hierop is een microfoon aangesloten. De microfoon zet geluid om in elektrische stroompjes. Deze stroompjes worden zichtbaar gemaakt op het scherm van de oscilloscoop. Links zien we een zogenaamde stemvork. Dit is een simpel metalen instrument dat met een hamertje aangeslagen kan worden. De stemvork produceert dan de "nette" toon die op het scherm zichtbaar is.
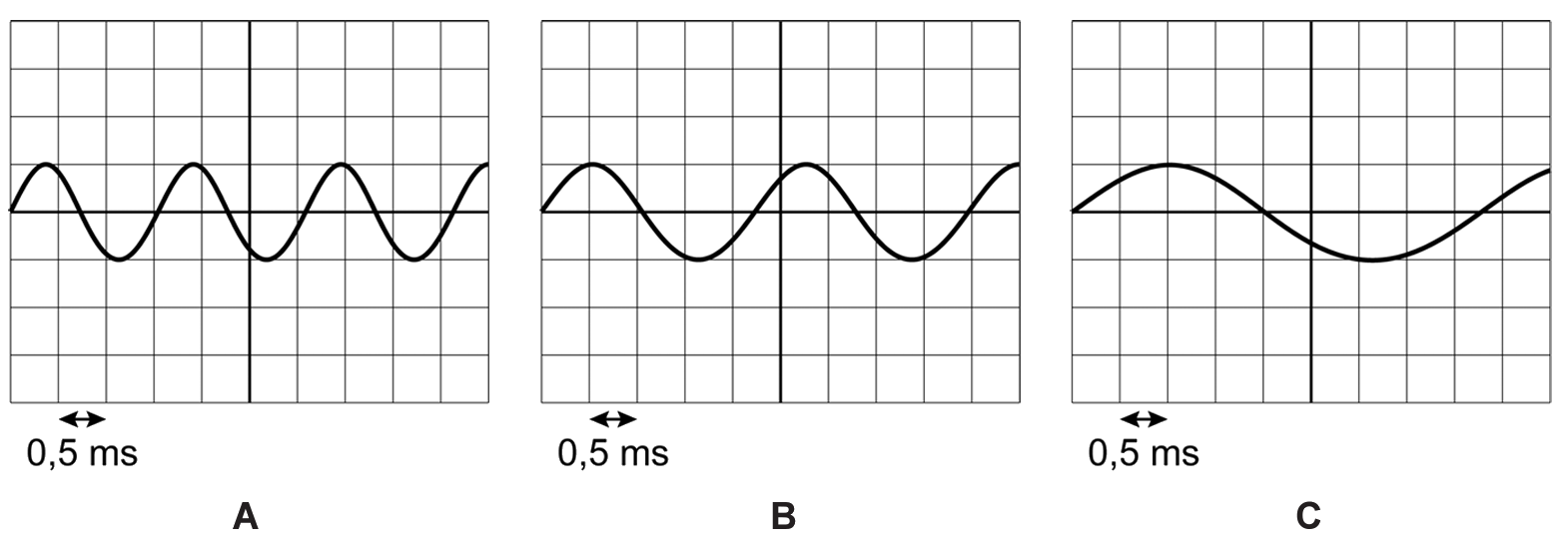
Laten we eens het oscilloscoopbeeld van een aantal tonen vergelijken. Hieronder zien we aan de linkerzijde een oscilloscoopbeeld van een zachte en een harde toon. Zoals je kunt zien heeft een zachte toon een kleine amplitude en heeft de harde toon een grote amplitude. Hoe "hard" het geluid is, noemen we in de natuurkunde de geluidsterkte. We meten de geluidsterkte in decibel (dB). Aan de rechterkant zien we een oscilloscoopbeeld van een lage en een hoge toon. Zoals je kunt zien heeft een lage toon een lage frequentie (en een grote trillingstijd) en heeft een hoge toon een hoge frequentie (en een lage trillingstijd). De frequentie van een toon bepaald dus de toonhoogte van het geluid.
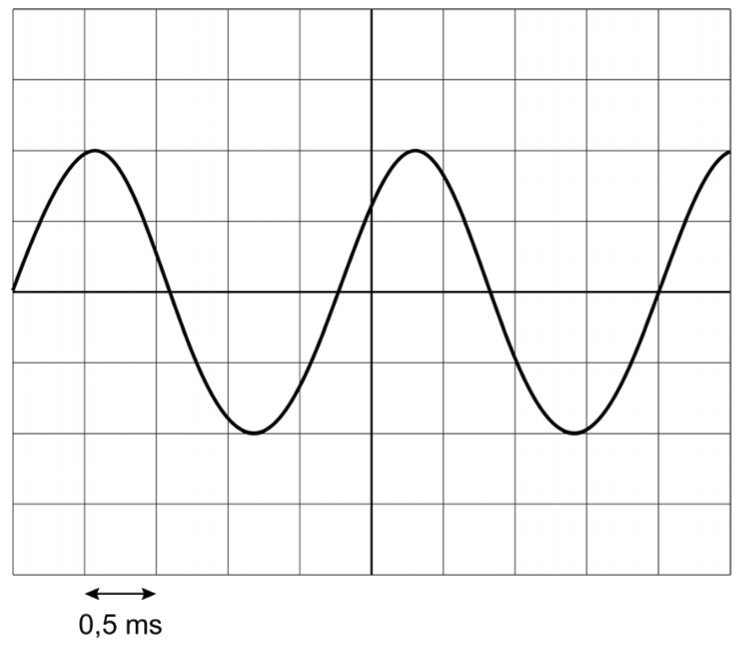
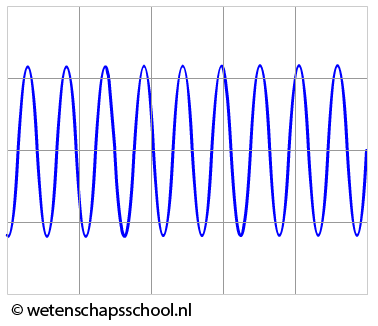
Als we kort een geluid maken, bijvoorbeeld door te drukken op een pianotoets of door het aanslaan van een snaar van een gitaar, dan zal de geluidsterkte naar verloop van tijd steeds kleiner worden. We zien dit effect in het onderstaande oscilloscoopbeeld. Zoals je kan zien wordt hier de amplitude steeds kleiner. De trillingstijd en de frequentie, en dus ook de toonhoogte, blijven gelijk.
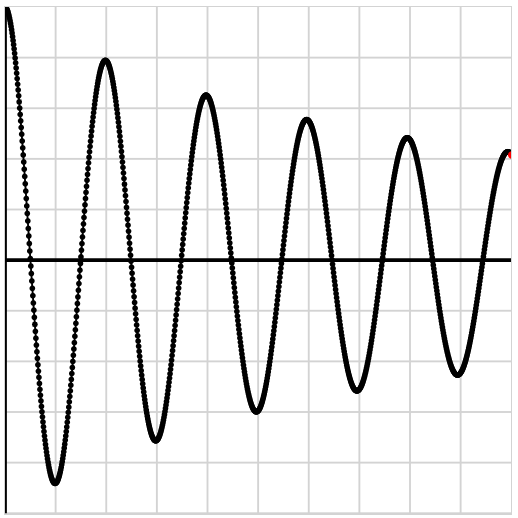
Het oscilloscoopbeeld kan worden opgevat als een diagram met op de horizontale as de tijd (t) en op de verticale as de uitwijking (u). We spreken hier daarom ook wel van een (u,t)-diagram. De onderstaande trilling herhaalt zich in de tijd. We noemen een dergelijke beweging een periodieke beweging. De trillingstijd (T) geeft aan hoe lang het duurt voordat de beweging zich herhaalt. We noemen de trillingstijd ook wel de periode. In de bovenstaande afbeelding zien we twee manieren om de trillingstijd te meten.
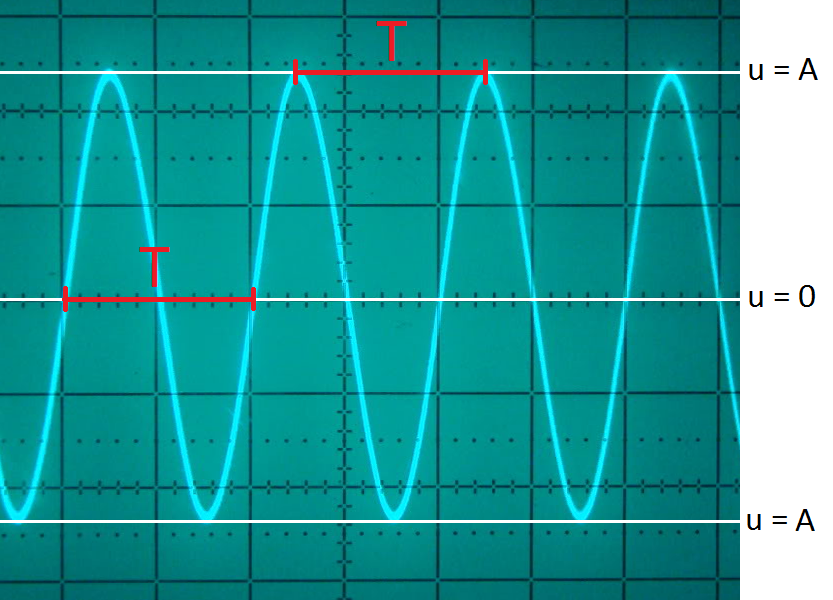
De grootte van elk hokje op de horizontale as van het oscilloscoopbeeld wordt gemeten in ms/div. "div" staat hier voor "division", hetgeen we in het Nederlands "hokje" zouden noemen. Een waarde van 10 ms/div betekent bijvoorbeeld dat elk hokje op de horizontale as overeenkomt met 10 milliseconden.
Met de trillingstijd kunnen we o.a. de frequentie (f) bepalen. We meten de frequentie in hertz (Hz) en dit komt overeen met het aantal trillingen per seconde. Hier geldt:
$$ f = \frac{1}{T} \,\,\,\,\,\text{(SI-eenheden)} $$
|
Let erop dat je de trillingstijd in deze formule altijd in seconden invult. De trillingstijd wordt ook vaak gegeven in milliseconden (ms). Er geldt:
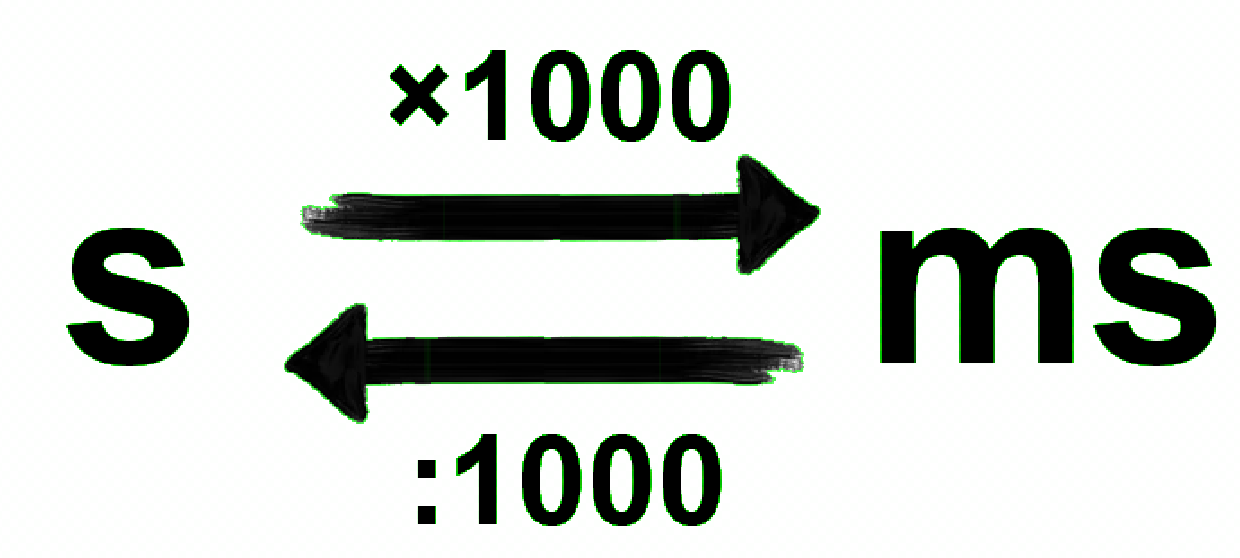
Aan de formule kan je zien dat een grotere frequentie altijd zorgt voor een kleinere trillingstijd en andersom.
|
Voorbeeld
|
|
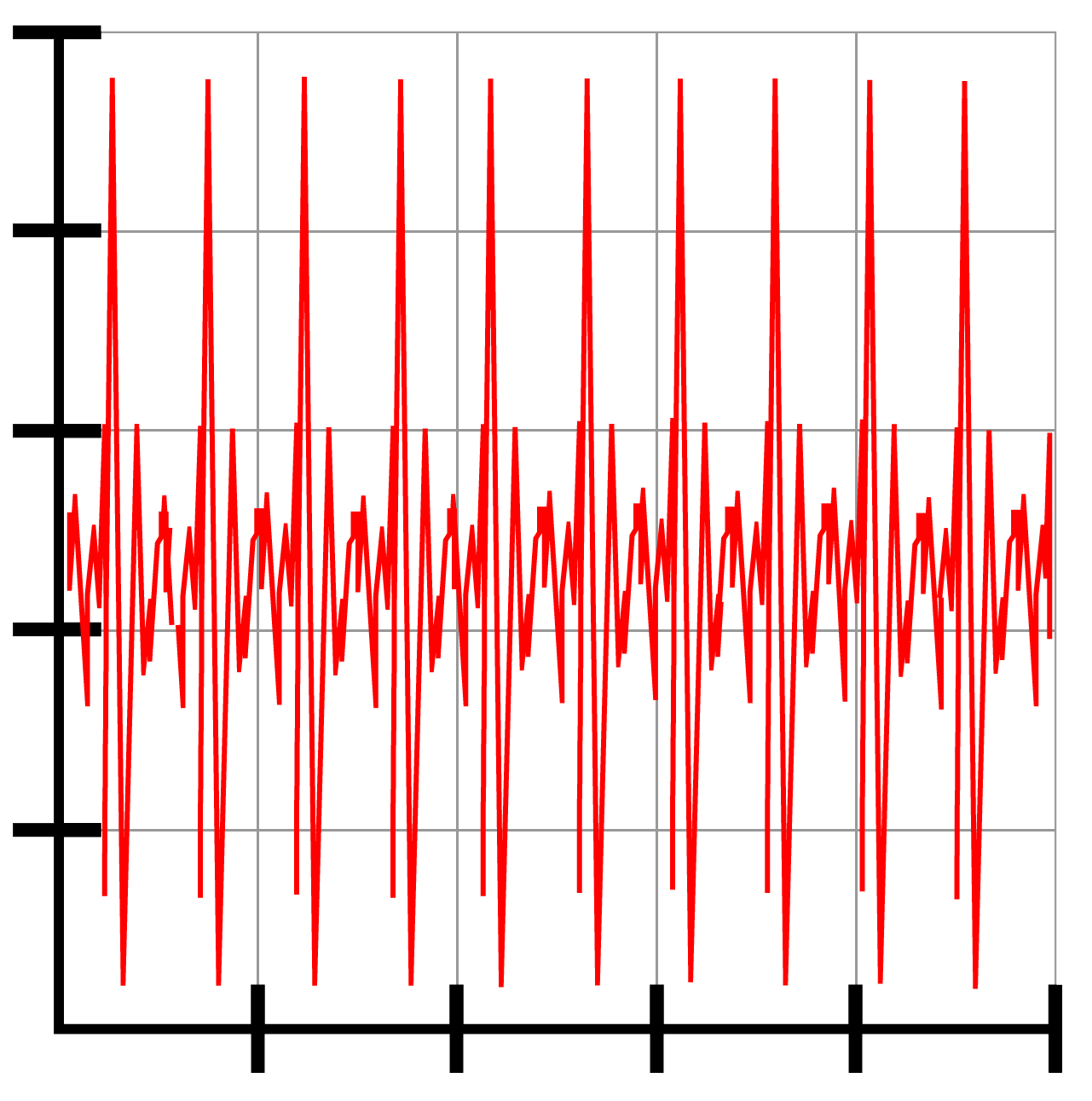
Vraag: Vraag: Bepaal de frequentie van het onderstaande oscilloscoopbeeld van een saxofoon. De oscilloscoop is ingesteld op 5 ms/div.
Antwoord: De tijdsduur behorende bij één trilling is in dit geval lastig nauwkeurig af te lezen. Het is hier daarom noodzakelijk om de trillingstijd van zoveel mogelijk trillingen tezamen te meten. Als we netjes meten, dan vinden we bijvoorbeeld dat 10 trillingen overeenkomen met 4,75 hokjes (ga dit zelf na). Eén trilling komt dan overeen met: $$ \frac{4,75}{10} = 0,475 \text{ hokjes} $$Omdat de oscilloscoop is ingesteld op 5 milliseconde per hokje, vinden we: $$ 0,475 \times 5 = 2,375 \text{ ms} $$In seconden wordt dit: $$ T = \frac{2,375}{1000} = 0,002375 \text{ s} $$Met de formule voor de frequentie vinden we dan: $$ f = \frac{1}{T} \;\;\;\;\;\;\;\; f = \frac{1}{0,002375} = 421 \text{ Hz} $$
|
INSTRUCTIE:
Trillingen
|
Leerdoelen:
|
|
|
Opdrachten
|
|
§3 Golven
In deze paragraaf gaan we rekenen met de golfsnelheid en de golflengte.
Voor de snelheid van een golf gebruiken we de formule voor de snelheid uit het hoofdstuk "beweging":
$$ v_{golf} = \frac{\Delta x}{\Delta t} $$In de tabel achter in het boek kan je voor een aantal stoffen de geluidsnelheid opzoeken. Deze geluidsnelheid is afhankelijk van de temperatuur. Let erop dat de temperaturen gegeven zijn in kelvin (K). Je kan als volgt graden Celsius omschrijven naar kelvin:
| $$ 0 \text{ K} = -273\,^{\circ}\text{C} $$ |
Stel dat we lezen dat de temperatuur van lucht 20 oC is. Dit is gelijk aan 20 + 273 = 293 K. Volgens de tabel achter in het boek hoort bij deze temperatuur een geluidsnelheid van 0,343 x 103 m/s. Dit is gelijk aan 343 m/s. Als in de vraag een temperatuur genoemd wordt, is dit dus vaak een aanwijzing dat de geluidsnelheid opgezocht moet worden.
|
Voorbeeld
|
|
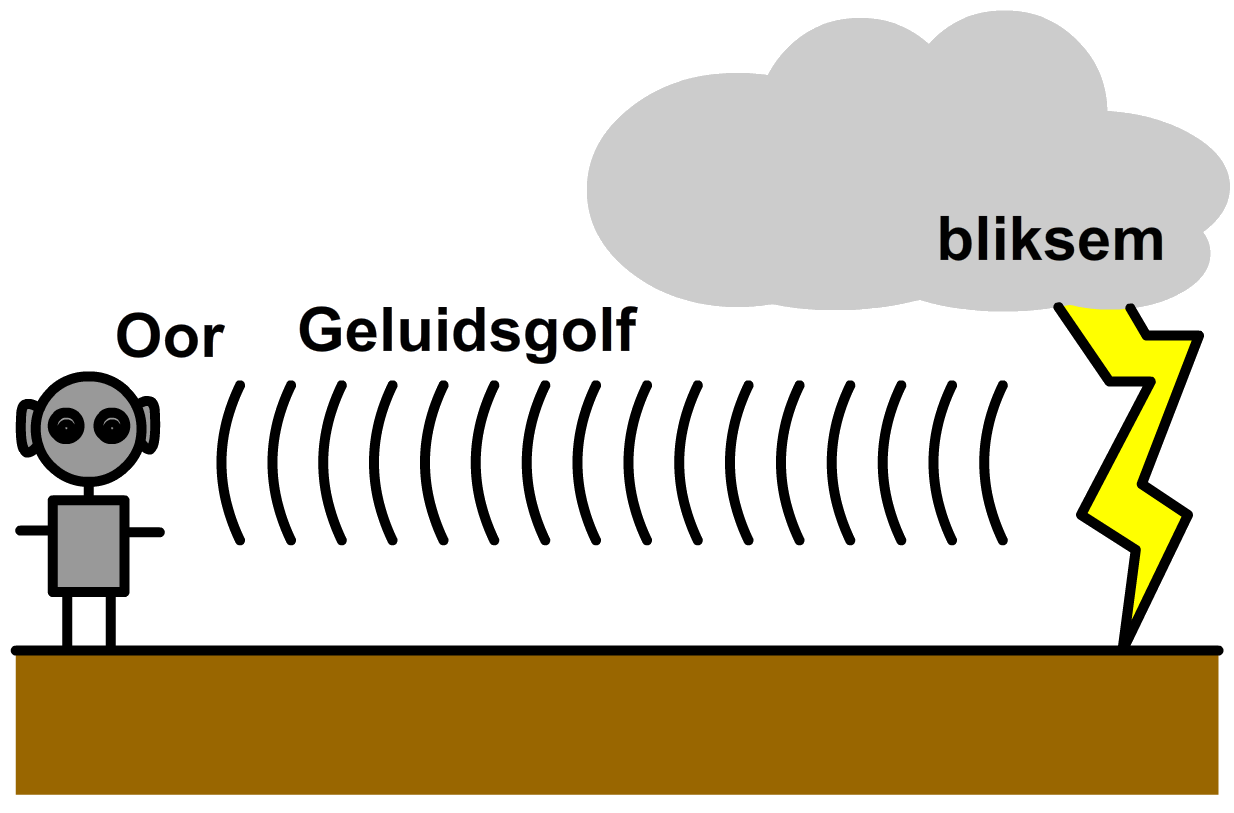
Vraag: Je ziet tijdens een hevige storm een bliksemflits. 8 seconden later hoor je de bijbehorende knal. Bereken hoe ver de bliksem van je vandaan was. De temperatuur van de lucht is 20 oC.
Antwoord: Eerst noteren we de gegevens: tijd = 8 s Volgens BINAS geldt voor lucht van 20 graden Celsius (293 K): snelheid = 343 m/s Nu kiezen we de juiste formule en vullen deze in: $$\text{afstand} = \text{snelheid} \times \text{tijd} $$ $$ \text{afstand} = 343 \times 8 = 2744 \text{ m} $$De bliksem vond dus op een afstand van 2744 meter plaats.
|
In het volgende voorbeeld gaan we redeneren met het begrip echo. Zoals je waarschijnlijk wel weet is een echo een reflectie van geluid tegen een oppervlak.
|
Voorbeeld
|
|
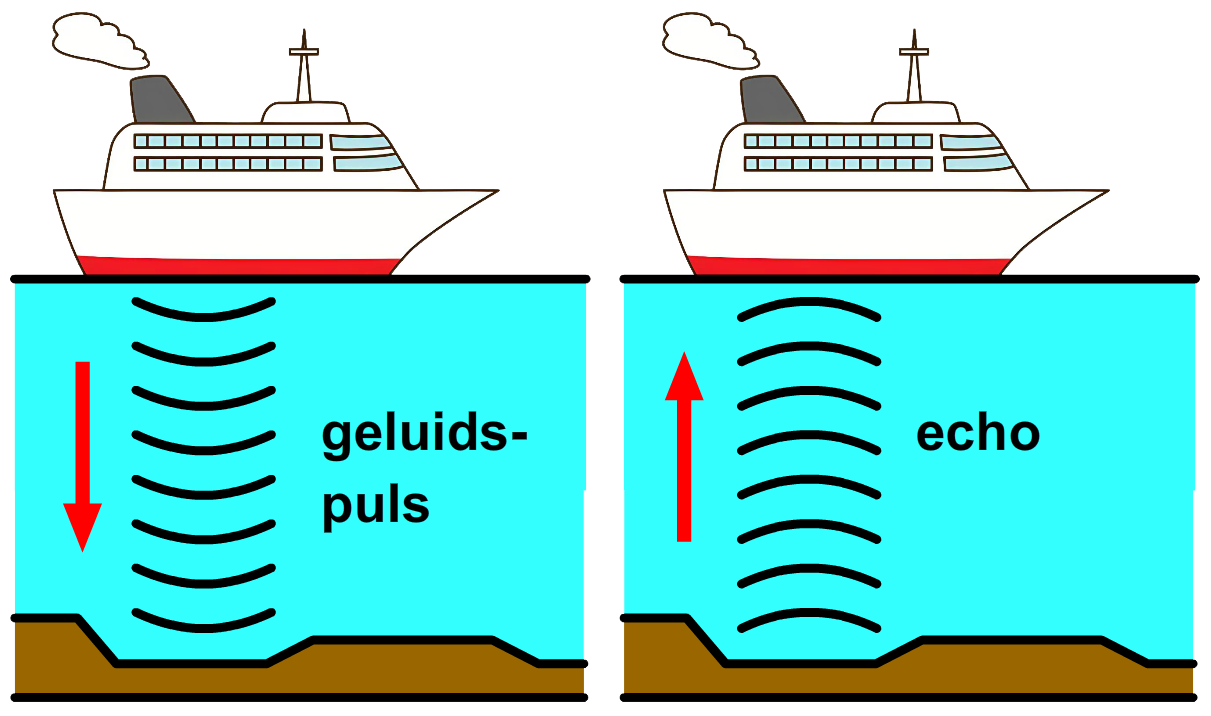
Vraag: Met behulp van echo kan men bepalen hoe diep de zeebodem is. Men stuurt aan de onderkant van een schip een geluidspuls naar beneden en meet hoelang het duurt voordat de puls tegen de bodem reflecteert en terugkomt bij het schip. De puls doet er 0,59 s over om terug te komen bij het schip. Bereken hoe diep de zeebodem is.
Antwoord: Het geluid beweegt eerst naar de zeebodem en daarna weer terug. Dit duurt 0,59 s. We willen weten hoelang het geluid erover doet om alleen de weg naar beneden af te leggen. Hiervoor delen we door twee: tijd = 0,59 / 2 = 0,295 s Volgens BINAS geldt voor zeewater: snelheid = 1510 m/s (BINAS) Nu kiezen we de juiste formule en vullen deze in: $$\text{afstand} = \text{snelheid} \times \text{tijd} $$ $$ \text{afstand} = 1510 \times 0,295 = 445 \text{ m} $$De zeebodem is dus 445 meter diep.
|
We kunnen deze formule ook nog herschrijven in twee andere vormen. We hebben hiervoor het begrip golflengte nodig. De lengte van een golf noemen we de golflengte (λ). Hieronder is de golflengte aangegeven bij zowel een golf in een touw als een geluidsgolf. Bij geluidsgolven is de golflengte gelijk aan de afstand tussen twee opeenvolgende plekken met een maximale of een minimale dichtheid (zie de rechter afbeelding).
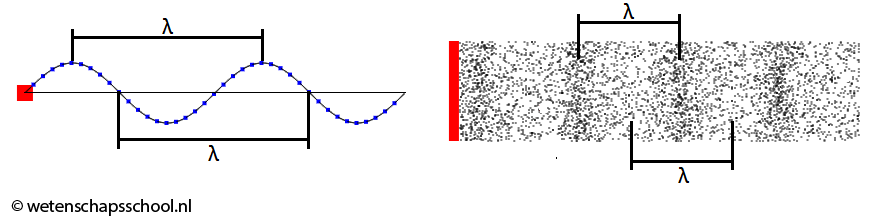
Met behulp van de golflengte kunnen we de formule voor de golfsnelheid herschrijven als:
$$ v_{golf} = \frac{\lambda}{T} $$
|
Omdat f = 1/T, kunnen we deze formule ook schrijven als:
$$ v_{golf} = \lambda f $$
|
In de tabel achter in het boek kan je voor een aantal stoffen de geluidsnelheid opzoeken. Deze geluidsnelheid is afhankelijk van de temperatuur. Let erop dat de temperaturen gegeven zijn in kelvin (K). Je kan als volgt graden Celsius omschrijven naar kelvin:
| $$T(K) = T(^\circ C) + 273$$ |
T(K) staat voor de temperatuur in kelvin. T(oC) staat voor de temperatuur in graden Celsius. Stel dat we lezen dat de temperatuur van lucht 20 oC is. Dit is gelijk aan 20 + 273 = 293 K. Volgens de tabel achter in het boek hoort bij deze temperatuur een geluidsnelheid van 0,343 × 103 m/s. Dit is gelijk aan 343 m/s. Als in de vraag een temperatuur genoemd wordt, is dit dus vaak een aanwijzing dat de geluidsnelheid opgezocht moet worden.
INSTRUCTIE:
Golven
|
Leerdoelen:
|
|
|
Opdrachten
|
|
| BINAS: | |
| 15 | Geluidsnelheden |