Hoofdstuk 2
Beweging
§1 Snelheid
§2 Gemiddelde snelheid
§3 Grafieken
§4 Het (x,t)-diagram
§5 Het (v,t)-diagram
§1 Snelheid
In dit hoofdstuk gaan we bewegingen bestuderen. Je kan hier denken aan het bewegen van een raket in een baan om de maan of gewoon het fietsen van huis naar school. In deze eerste paragraaf gaan we leren de snelheid te berekenen. We gaan dit doen in zowel meter per seconde als kilometer per uur.
Als een voorwerp met een constante snelheid beweegt, dan kunnen we deze snelheid uitrekenen met de volgende formule:
$$ v = \frac{\Delta x}{\Delta t} $$
| Snelheid (v) |
meter per seconde (m/s) |
| Verplaatsing (Δx) |
meter (m) |
| Tijdsduur (Δt) |
seconde (s) |
|
De x staat voor de positie van een voorwerp. Het Δ-teken staat voor "de toename van". Δx staat dus voor de toename van de positie tijdens de beweging. We noemen dit ook wel de verplaatsing.
Δt staat voor de toename van de tijd tijdens de beweging. We noemen dit ook wel de tijdsduur.
 Stappenplan: Rekenen met snelheid
Stappenplan: Rekenen met snelheid
|
|
Vraag:
Een sprinter rent 100 meter met een snelheid van 10,5 m/s. Bereken na hoeveel seconden de sprinter de finish haalt.
Stap 1: Gegevens (G)
Schrijf de gegevens uit de vraag op:
Δx = 100 m
v = 10,5 m/s
Δt = ... s
Stap 2: Omschrijven (O)
Reken de gegevens zoveel mogelijk om in dezelfde eenheden. In dit geval staan alle gegevens al in meters en seconden, dus deze stap kunnen we overslaan.
Stap 3: Formule (F)
Noteer de formule in de juiste vorm. In dit geval willen we de tijdsduur (Δt) weten:
$$ \Delta t = \frac{\Delta x}{v} $$
Stap 4: Invullen en Rekenen (IR)
Vul de formule in:
$$ \Delta t = \frac{100}{10,5} = 9,52 \text{ s} $$
De sprinter heeft er dus 9,52 s over gedaan.
Stap 5: Eenheid (E)
Noteer de eenheid achter het antwoord. In dit geval is de eenheid s.
|
De SI-eenheid van de snelheid is meter per seconde, maar in het dagelijks leven wordt ook vaak kilometer per uur gebruikt. We kunnen bij het omschrijven gebruik maken van de volgende regel:
|

|
 Stappenplan: Rekenen met snelheid
Stappenplan: Rekenen met snelheid
|
|
Vraag:
Een leerling is aan het hardlopen. Zijn doel is om binnen drie minuten 1,0 kilometer te rennen. De leerling rent 3,0 minuten lang met een snelheid van 18 km/h. Bereken of de leerling zijn doel bereikt heeft.
Stap 1: Gegevens (G)
Schrijf de gegevens uit de vraag op en reken ze zoveel mogelijk om in dezelfde eenheden. In dit voorbeeld kiezen we voor meter en seconde:
Δt = 3,0 min
v = 18 km/h
Δx = ... m
Stap 2: Omschrijven (O)
Reken de gegevens zoveel mogelijk om in dezelfde eenheden. In dit geval rekenen we alles om naar meters en seconden. Omdat er 60 seconden in een minuut zitten, vinden we:
Δt = 3,0 × 60 = 180 s
v = 18 / 3,6 = 5,0 m/s
Stap 3: Formule (F)
Schrijf de formule nu om in de juiste vorm. In dit geval willen de verplaatsing (Δx) berekenen:
$$ \frac{\Delta x}{\Delta t} = v \;\;\;\;\; \rightarrow \;\;\;\;\; \Delta x = v \times \Delta t $$
Stap 4: Invullen en Rekenen (IR)
Vul de formule in:
$$ \Delta x = 5,0 \times 180 = 900 \text{ m} $$
Stap 5: Eenheid (E)
Denk aan de eenheid achter het antwoord. In dit geval is de eenheid m.
Stap 6: Conclusie (C)
Schrijf de conclusie op. Leg uit hoe je aan deze conclusie komt. Denk ook aan de eenheid achter het antwoord:
900 m is minder dan 1,0 kilometer, dus de leerling heeft zijn doel niet bereikt.
|
 INSTRUCTIE:
Rekenen met snelheid
INSTRUCTIE:
Rekenen met snelheid
 Leerdoelen:
Leerdoelen:
|
- Zorg dat je kan rekenen met de formule "v = Δx/Δt" en dat je deze formule kan omschrijven in de drie vormen.
- Zorg dat je km/h en m/s in elkaar kan omschrijven.
|
 Opdrachten
Opdrachten
|
- (1p) De maximumsnelheid voor verkeer binnen de bebouwde kom is 50 km/h. Reken dit om naar m/s.
- (1p) Een sprinter rent de honderd meter met een gemiddelde snelheid van 10 m/s. Reken dit om naar km/h.
- (1p) Een straaljager vliegt met 1500 km/h. Reken dit om naar m/s.
- (2p) De aarde draait met een snelheid van 30 km/s om de zon. Reken deze snelheid om naar km/h.
- (2p) Een auto rijdt in 30 seconden een afstand van 600 m. Bereken de snelheid van de auto.
- (2p) Mario rent 12 seconden lang met een snelheid van 6 m/s. Bereken hoeveel afstand hij heeft afgelegd.
-
(2p) In een populaire attractie in een pretpark wordt een ring met inzittenden met een constante snelheid van 1,5 m/s tot een hoogte van 67,5 m gebracht. Bereken de tijd die nodig is om de ring op deze hoogte te brengen.
(Bron: Examen VMBO-T, 2022-2)
- (3p) Een fietser rijdt 20 minuten lang met een constante snelheid. De snelheidsmeter geeft aan dat de fietser 24 km/h rijdt. Bereken welke afstand de fietser heeft afgelegd.
- (3p) Een auto rijdt met een snelheid van 100 km/h een afstand van 700 m. Bereken hoe lang de auto hierover doet.
- (3p) Een werper bij honkbal gooit een bal met een snelheid van 160 km/h naar de slagman. Deze staat op een afstand van 18,45 m. Bereken na hoeveel seconden de bal bij de slagman is.
- (4p) Een leerling is aan het hardlopen. Zijn doel is om binnen 50 seconden 200 meter te rennen. De leerling rent met een snelheid van 16 km/h. Bereken of de leerling zijn doel bereikt heeft.
- (3p) Een Boeing vliegt binnen 55 minuten van Amsterdam naar Londen. De afstand tussen de vliegvelden is 358 kilometer. Bereken de gemiddelde snelheid van het vliegtuig.
- (3p) De snelheid van geluid in lucht is 340 m/s. Het onweert 8 km verderop. Bereken hoelang het duurt voordat je de donder hoort.
- (3p) Een kogel wordt met een snelheid van 550 km/h uit een geweer weggeschoten. Al na 0,75 s raakt de kogel zijn doel. Bereken de afstand tussen geweer en doel.
|
§2 Gemiddelde snelheid
In deze paragraaf gaan we leren rekenen met de gemiddelde snelheid. We introduceren twee formules waarmee we dit kunnen doen.
Als de snelheid van een voorwerp niet constant is, dan vinden we met de formule uit de vorige paragraaf de gemiddelde snelheid:
$$v_{gem} = \frac{\Delta x}{\Delta t}$$
| Gemiddelde snelheid (vgem) |
meter per seconde (m/s) |
| Verplaatsing (Δx) |
meter (m) |
| Tijdsduur (Δt) |
seconde (s) |
|
Als een voorwerp geleidelijk versnelt of vertraagt, dan spreken we van een eenparige versnelling. In dit geval kunnen we de gemiddelde snelheid ook als volgt uitrekenen:
$$v_{gem} = \frac{v_{b}+v_{e}}{2} \;\;\;\; \text{(eenparige versnelling)} $$
| Beginsnelheid (vb) |
meter per seconde (m/s) |
| Eindsnelheid (ve) |
meter per seconde (m/s) |
| Gemiddelde snelheid (vgem) |
meter per seconde (m/s) |
|
Stel dat een auto bijvoorbeeld eenparig versnelt van 10 m/s naar 30 m/s, dan is de gemiddelde snelheid gelijk aan:
$$ v_{gem} = \frac{v_b+v_e}{2} = \frac{10+30}{2} = 20 \text{ m/s} $$
Let erop dat je als volgt haakjes gebruikt in je rekenmachine:
$$ (10 + 30 )/2 = 20 \;\;\;\;\;\;\; \text{ rekenmachine} $$
 Voorbeeld
Voorbeeld
|
|
Opdracht:
Een auto versnelt gedurende 10 seconden van 20 naar 30 m/s. De versnelling is eenparig. Bereken hoeveel meter de auto heeft afgelegd.
Antwoord:
Eerst berekenen we de gemiddelde snelheid:
$$v_{gem} = \frac{v_{\text{begin}}+v_{\text{eind}}}{2} $$
$$v_{gem} = \frac{20 + 30}{2} = 25 \text{ m/s}$$
Met de gemiddelde snelheid kunnen we de afstand uitrekenen. Hiervoor schrijven we eerst de formule in de juist vorm:
$$ v_{gem} = \frac{\Delta x}{\Delta t} \;\;\rightarrow \;\; \Delta x = v_{gem} \times \Delta t $$
Nu vullen we de formule in:
$$\Delta x = v_{gem} \times \Delta t $$
$$\Delta x = 25 \times 10 = 250 \text{ m}$$
De auto heeft tijdens de versnelling dus 250 m afgelegd.
|
 INSTRUCTIE:
Gemiddelde snelheid
INSTRUCTIE:
Gemiddelde snelheid
 Leerdoelen:
Leerdoelen:
|
- Zorg dat je kan rekenen met de formules "vgem = Δx/Δt" en "vgem = (vb+ve)/2". De tweede formule geldt alleen bij een eenparige versnelling of vertraging.
- Zorg dat je weet dat bij een versnelling vanuit stilstand de beginsnelheid nul is (vb = 0) en dat bij remmen tot stilstand de eindsnelheid nul is (ve = 0).
|
 Opdrachten
Opdrachten
|
- (3p) Een auto versnelt eenparig in 12 seconden van 10 m/s naar 35 m/s. Bereken de afstand die de auto tijdens de beweging heeft afgelegd.
- (4p) Een auto trekt met een eenparige versnelling vanuit stilstand op tot 40 m/s en legt een afstand van 950 meter af. Bereken hoe lang de auto over de versnelling heeft gedaan.
- (4p) Een automobilist die met een snelheid van 80 km/h rijdt, trapt op zijn rem totdat hij eenparig tot stilstand is gekomen. Het remmen duurt 4,0 seconden. Bereken de remweg van de bestuurder.
- (5p) Een parachutespringer valt met een snelheid van 200 km/h. Dan trekt de springer zijn parachute open. Na 0,70 s is zijn snelheid eenparig afgenomen tot 40 km/h. Bereken hoeveel meter de parachutist in de tussentijd heeft afgelegd.
- (4p) Een persoon laat een bal vanuit stilstand vallen van een gebouw met een hoogte van 100 m. De bal versnelt hierdoor eenparig tot een snelheid van 44 m/s. Bereken de valtijd van de bal.
- (4p) Een auto trekt binnen 4,0 s op met een eenparige versnelling tot een snelheid van 70 km/h. Bereken welke afstand de auto heeft afgelegd tijdens het optrekken.
|
§3 Grafieken
In de volgende paragrafen gaan we beweging beschrijven met behulp van grafieken. Om dit goed te kunnen doen, gaan we eerst leren hoe je in de natuurkunde met behulp van meetwaarden een grafiek maakt.
Een goede manier om metingen weer te geven is met behulp van tabellen en grafieken. Hieronder zien we bijvoorbeeld een tabel met daarin de valtijd van een voorwerp bij verschillende hoogten. Belangrijk is om bij elke kolom de grootheid te schrijven en daarachter tussen haakjes de eenheid.
|
Hoogte (m)
|
Tijd (s)
|
|
0
|
0
|
|
5
|
1,0
|
|
10
|
1,4
|
|
15
|
1,7
|
|
20
|
2,0
|
|
25
|
2,3
|
|
30
|
2,1
|
|
35
|
2,7
|
|
40
|
2,9
|
Van deze tabel maken we de volgende grafiek:
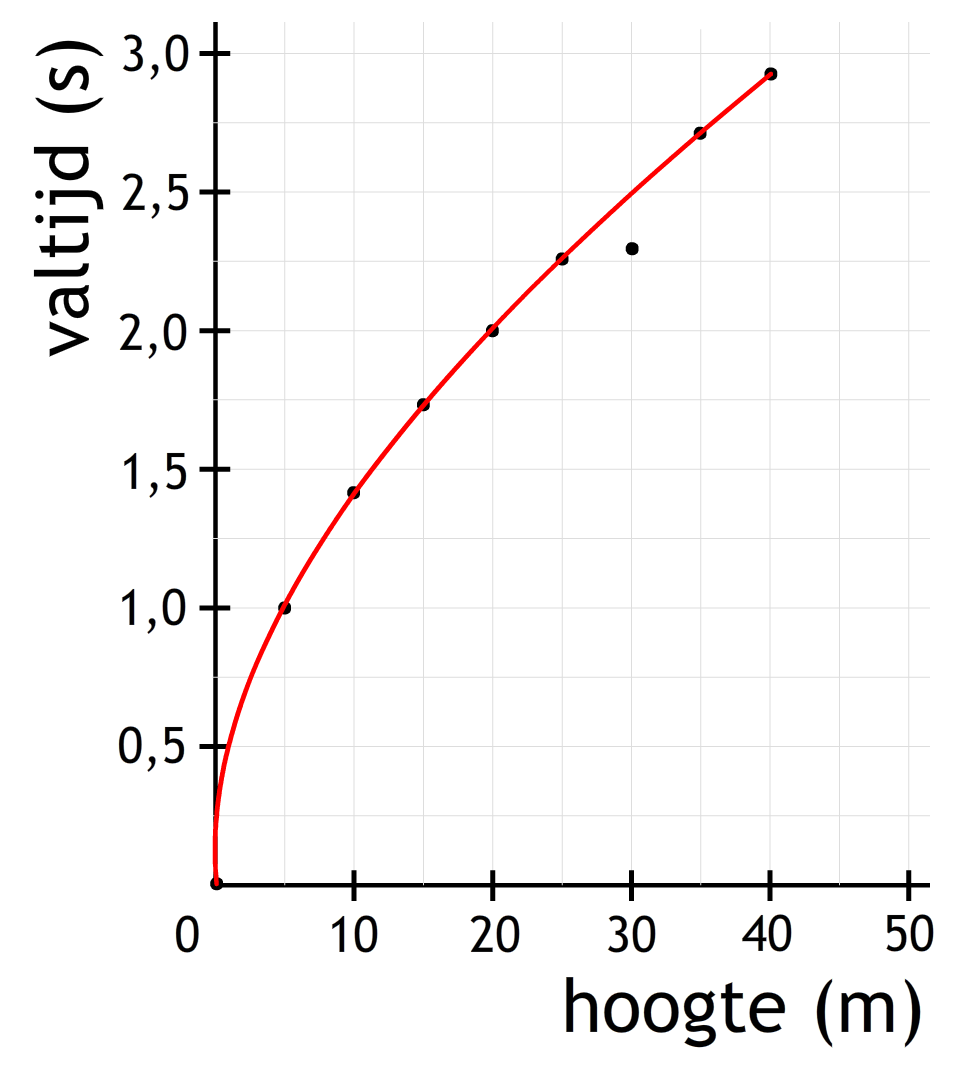
Er zijn een aantal belangrijke regels voor het maken van grafieken in de natuurkunde:
- Schrijf altijd de grootheden en tussen haakjes de eenheden bij de assen.
- Verdeel de assen in gelijke stapjes. Maak de stapjes niet te ingewikkeld. Neem dus bijvoorbeeld niet 0, 13, 26, 39, 52, 65 enzovoorts. Dit is lastig aflezen. Zorg ook dat de grafiek netjes in het diagram past. De grafiek mag niet veel kleiner zijn dan het diagram.
- Zet alle meetpunten zo precies mogelijk in het diagram.
- Trek dan een vloeiende lijn die zo goed mogelijk door de meetpunten loopt, maar zonder alle punten zigzaggend met elkaar te verbinden. We noemen dit ook wel de trendlijn. Het komt regelmatig voor dat een aantal punten niet op de vloeiende lijn ligt. Dit komt meestal door meetfouten. In het vorige voorbeeld zien we bijvoorbeeld een meetfout bij een hoogte van 30 meter.
- Als je de grafiek afleest, dan is het belangrijk niet naar de meetpunten te kijken, maar naar de trendlijn. De individuele meetpunten kunnen immers meetfouten bevatten.
 INSTRUCTIE:
Grafieken tekenen
INSTRUCTIE:
Grafieken tekenen
 Leerdoelen:
Leerdoelen:
|
- Zorg dat je tabellen en grafieken correct kan weergeven. Denk in beide gevallen aan het noteren van grootheden en eenheden en kies de assen zodat de grafiek mooi in het diagram past.
- Zorg dat je bij het maken van grafieken alle meetpunten zo precies mogelijk weergeeft en daarna een vloeiende trendlijn trekt. Punten die niet op de trendlijn liggen bevatten meetfouten.
|
 Opdrachten
Opdrachten
|
-
Een leerling pompt water met een constante snelheid uit een grote bak en meet om de paar seconden hoeveel water nog in de bak zit. De leerling zet zijn metingen in het volgende diagram.
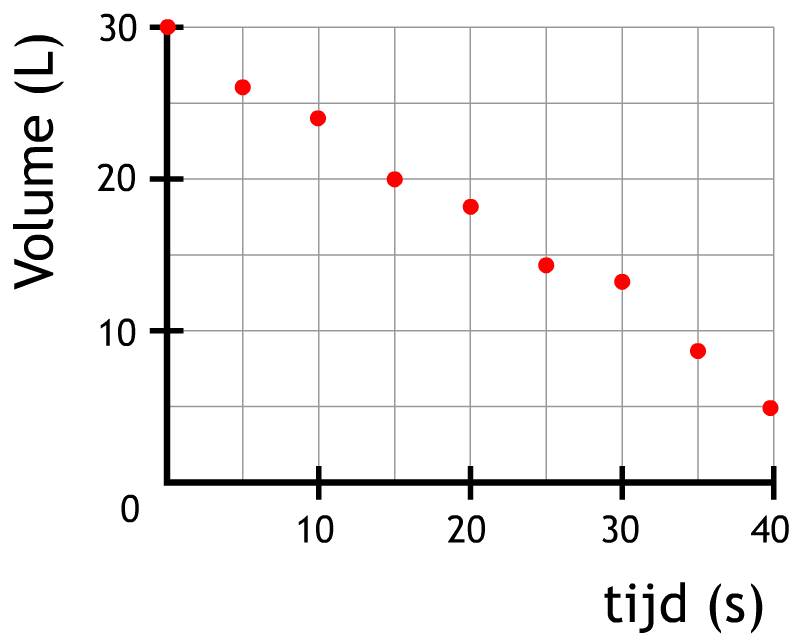
- (1p) Om de hoeveel tijd is een meting verricht?
- (1p) Teken de grafiek in het bovenstaande diagram.
- (1p) Omcirkel de grootste meetfout.
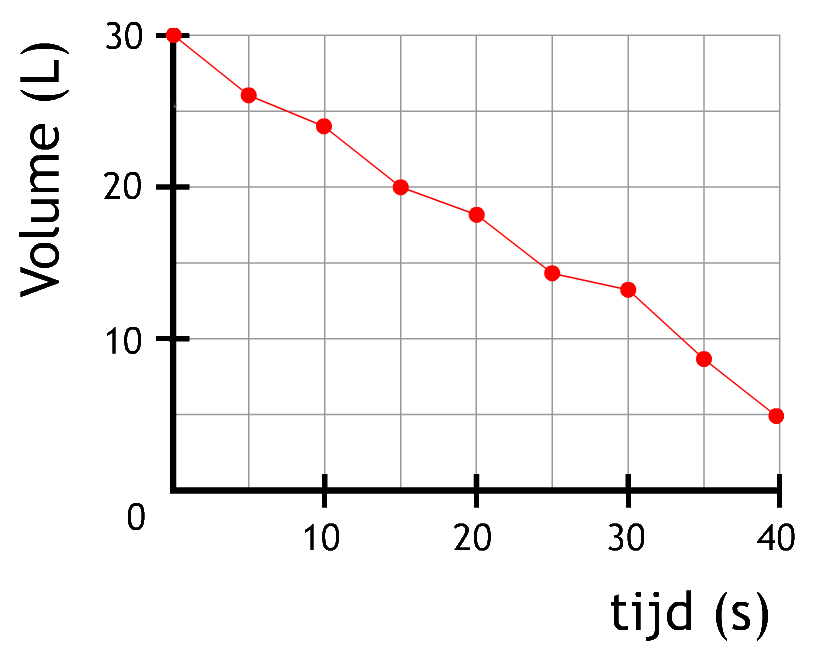
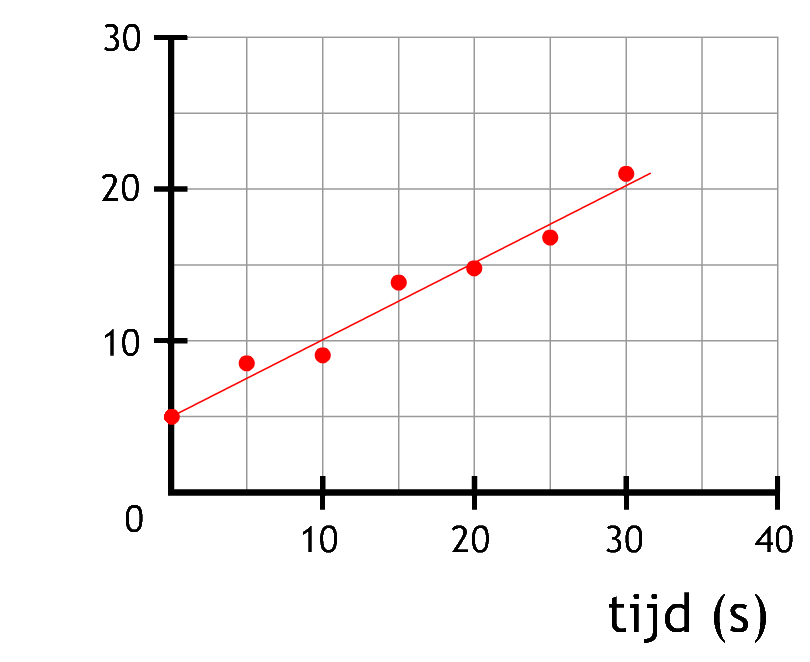
-
(6p) Geef bij de volgende diagrammen aan wat er ontbreekt of niet klopt:
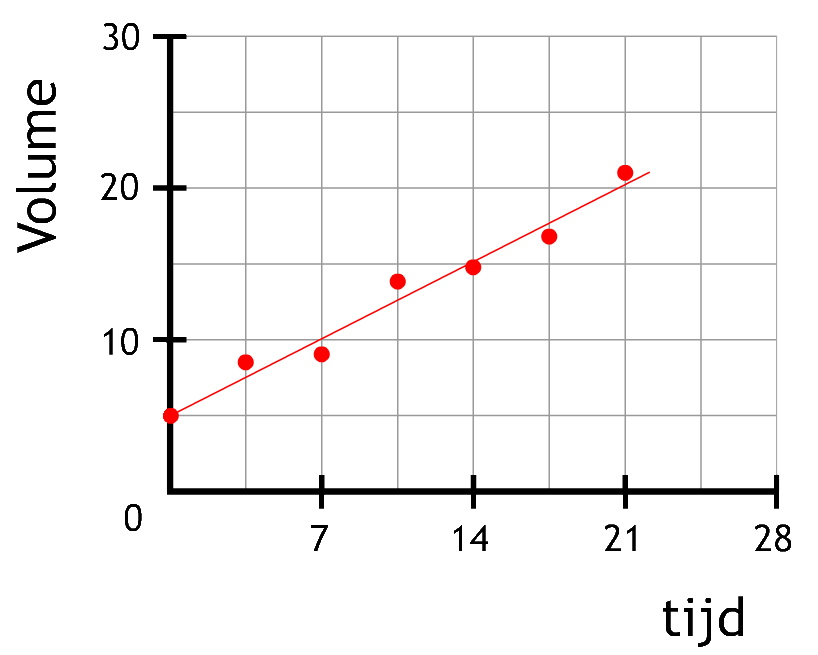
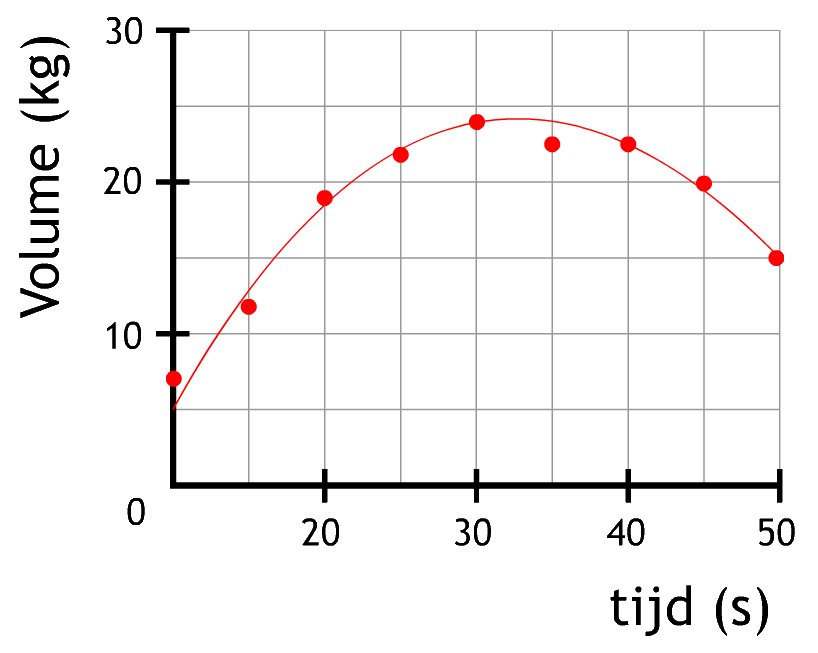
- (4p) Noteer vier dingen waar je op moet letten bij het maken van een grafiek in de natuurkunde.
-
De onderstaande foto van een vallende tennisbal is gemaakt met een stroboscoop. Dit is een lichtbron die snel aan en uit gaat. Elke keer dat het licht aanstaat, is de bal een stukje opgeschoven. In de onderstaande tabel is de positie van de bal weergegeven op verschillende momenten:
| Tijd(s) | Hoogte(m) |
| 0 | 12 |
| 0,2 | 11,6 |
| 0,4 | 10,8 |
| 0,6 | 9,7 |
| 0,8 | 8,1 |
| 1,0 | 6,1 |
| 1,2 | 1,0 |

- (4p) Teken het bijbehorende (hoogte,tijd)-diagram. Noteer de tijd bij de horizontale as.
- (1p) Leg uit hoe je aan de foto kan zien dat de bal een versnelling ondergaat tijdens het vallen.
- (1p) Leg aan de hand van de grafiek uit hoe je kan zien dat de bal een versnelling ondergaat tijdens het vallen.
- (1p) Omcirkel de grootste meetfout.
-
Een speelgoedwagentje wordt van verschillende hoogten losgelaten op een helling. Telkens wordt met een stopwatch gemeten hoelang het duurt voordat de kar beneden is.
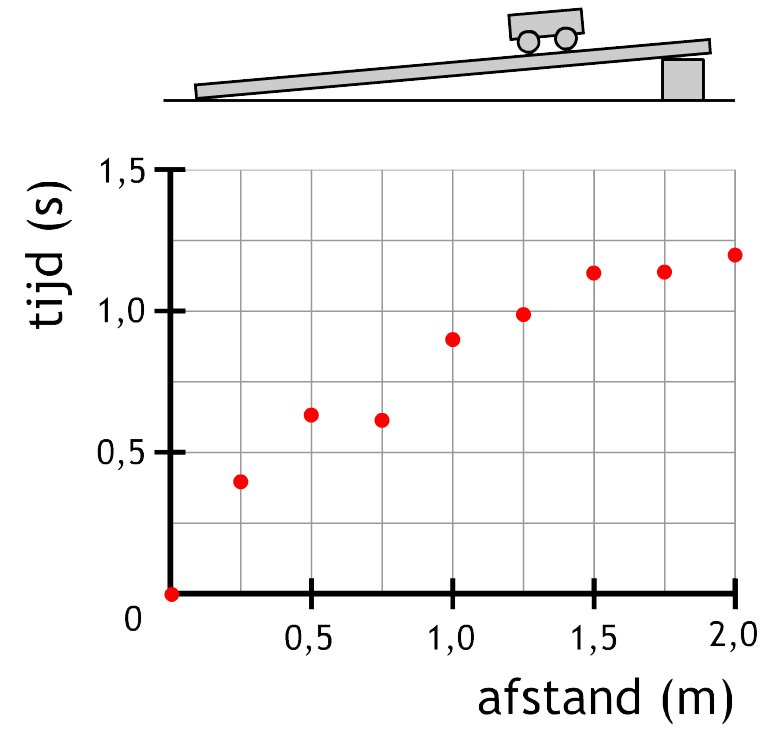
- (1p) De meetpunten van het experiment zijn in het bovenstaande diagram afgebeeld. Voeg nu ook de grafiek toe.
- (1p) Omcirkel de grootste meetfout.
- (2p) Lees af hoelang de kar erover doet om van de helling te komen bij een afstand van 0,75 meter.
- (1p) Hoe kan je aan de grafiek zien dat de kar steeds sneller van de helling beweegt?
-
Hieronder is een afbeelding te zien waarbij de beweging van een stuiterende basketbal is vastgelegd. Er zijn hierbij snel achter elkaar meerdere foto's gemaakt en deze foto's zijn daarna gecombineerd tot één beeld. Tussen de frames zit telkens 0,075 seconde.
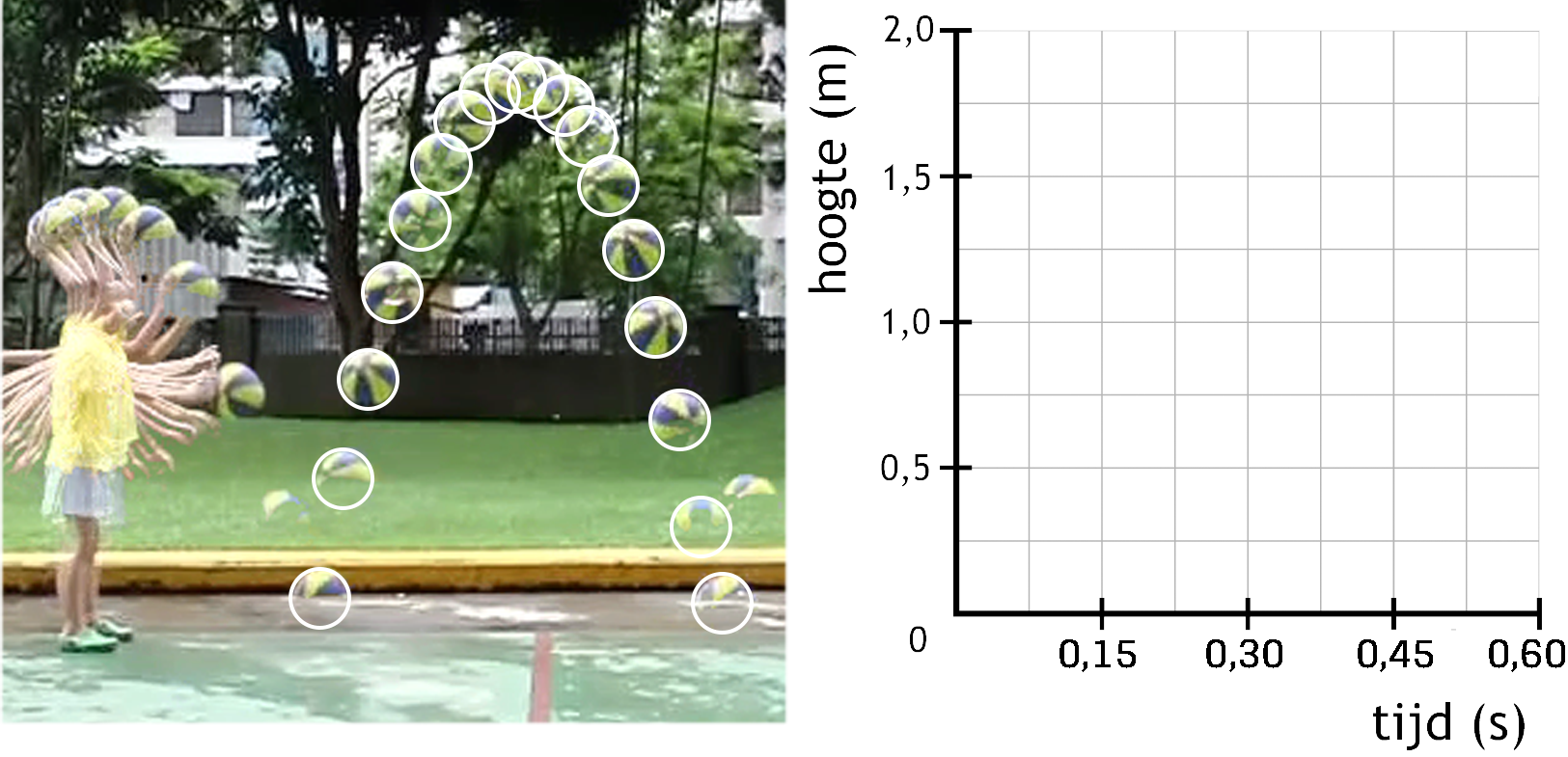
- (1p) Leg uit waarom in de foto de ballen zich dichter bij elkaar bevinden bovenaan de beweging.
- (4p) Bij een deel van de beweging is de bal omcirkelt. Teken een grafiek behorende bij dit deel van de beweging. Voor de hoogte is in zowel de foto als het diagram dezelfde schaal gekozen. Neem voor de positie van de bal telkens het midden van de bal.
-
Een leerling heeft vier voorwerpen van een onbekend materiaal. De leerling meet de massa en het volume van deze voorwerpen en schrijft de meetgegevens in de onderstaande tabel:
|
massa (g)
|
volume (cm3)
|
|
10
|
17
|
|
20
|
52
|
|
60
|
103
|
|
80
|
138
|
- (3p) Maak een diagram bij deze tabel met op de horizontale as de massa en op de verticale as het volume.
- (1p) Omcirkel de grootste meetfout.
- (3p) Van welk materiaal zouden deze voorwerpen gemaakt kunnen zijn?
- (6p) Teken een grafiek waarin je het verband weergeeft tussen de massa en het volume van lood. Zet op de horizontale as de massa in kg en laat dit lopen van 0 tot 30 kg in stapjes van 10 kg.
-
Een heliumballon stijgt op in de atmosfeer. Bevestigd aan de ballon zit een klein apparaatje waarmee om de paar kilometer de dichtheid van de lucht in de atmosfeer gemeten wordt. De meetgegevens staan in de onderstaande tabel:
|
Hoogte (km)
|
Dichtheid lucht (kg/m3)
|
|
2,5
|
0,94
|
|
5,0
|
0,69
|
|
7,5
|
0,50
|
|
10,0
|
0,37
|
|
12,5
|
0,27
|
|
15,0
|
0,19
|
- (3p) Teken de grafiek met op de horizontale as de hoogte en op de verticale as de dichtheid.
- (4p) De ballon heeft een massa van 6,0 gram en is met 12,0 liter helium gevuld. Bepaal met behulp van de grafiek hoe hoog de heliumballon maximaal zal opstijgen.
|
§4 Het (x,t)-diagram
Behalve met formules, kunnen we beweging ook beschrijven met grafieken. In deze paragraaf gaan we kijken naar de zogenaamde (x,t)-diagrammen.
Een (x,t)-diagram is een diagram met op de horizontale as de tijd (t) en op de verticale as de positie (x). Hieronder zijn een aantal bewegingen beschreven met behulp van dit type diagram. Links zien we een grafiek die horizontaal loopt. De positie x verandert hier niet in de tijd. Het voorwerp staat hier dus stil. In de tweede afbeelding zien we een voorwerp dat zich geleidelijk verplaatst. Elke seconde wordt er evenveel meter afgelegd. We spreken hier van een constante snelheid of van een eenparige beweging.
HIER IMAGES BOOK !!!
In de onderstaande linker afbeelding zien we een grafiek die steeds steiler gaat lopen. We zien dat in de eerste drie seconden slechts 0,5 meter wordt afgelegd en dat in de laatste drie seconden wel 4,5 m wordt afgelegd. Er geldt dus:
- Hoe steiler de lijn loopt, hoe sneller het voorwerp verplaatst.
We hebben hier dus te maken met een versnelling. Rechts zien we een grafiek die steeds minder steil gaat lopen. Hier hebben we dus te maken met een vertraging.
HIER IMAGES BOOK !!!
 Voorbeeld
Voorbeeld
|
|
Opdracht:
In het onderstaande (x,t)-diagram is de beweging van een fietser weergegeven. Beschrijf deze beweging in detail.
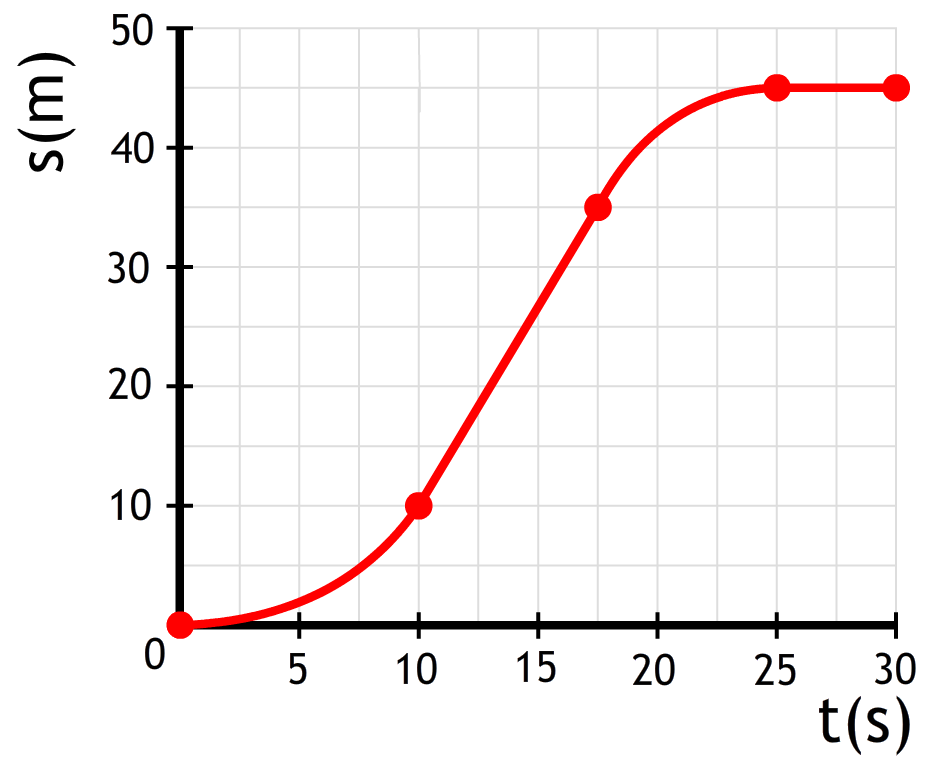
Antwoord:
In de eerste 10 seconden loopt de grafiek steeds steiler. De fietser ondergaat hier dus een versnelling. In de 7,5 seconden daarna blijft de grafiek even steillopen. We hebben hier dus te maken met een constante snelheid. In de 7,5 seconden daarna loopt de grafiek steeds minder steil. Hier hebben we dus te maken met een vertraging. In de laatste 5 seconden loopt de grafiek horizontaal. Hier hebben we dus te maken met stilstand.
|
 Voorbeeld
Voorbeeld
|
|
Opdracht:
In het onderstaande (x,t)-diagram is de beweging van een stuiterbal weergegeven. Beschrijf deze beweging in detail.
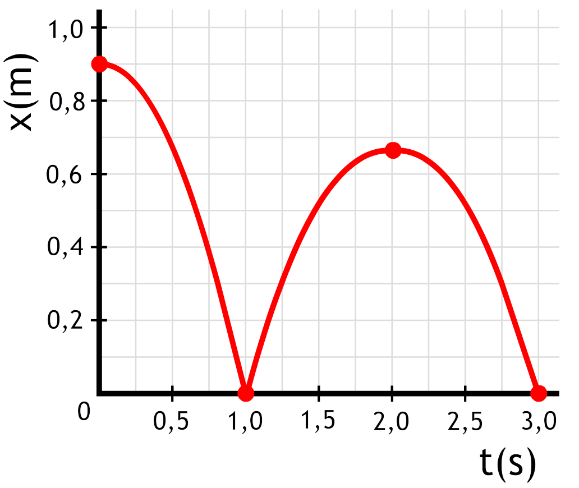
Antwoord:
In de eerste seconde loopt de grafiek steeds steiler. We hebben hier dus te maken met een versnelling. De stuiterbal gaat hier naar beneden. Op tijdstip t = 1,0 s komt de bal tegen de grond aan en gaat daarna omhoog. In de tweede seconde loopt de grafiek steeds minder steil. Hier hebben we dus te maken met een vertraging. De stuiterbal gaat hier omhoog. Op tijdstip t = 2,0 s loopt de grafiek even horizontaal. Hier staat de stuiterbal dus een moment stil op het hoogste punt van de beweging. In de derde seconde hebben we net als in de eerste seconde te maken met een versnelling naar beneden.
|
Met behulp van een (x,t)-diagram kunnen we ook de snelheid uitrekenen. In het onderstaande diagram is de verplaatsing Δx gelijk aan 4,0 meter. De tijdsduur Δt van de beweging is 6,0 seconden. De snelheid is dus gelijk aan:
$$ v = \frac{\Delta x}{\Delta t} $$
$$ v = \frac{4,0}{6,0} = 0,67 \text{ m/s}$$
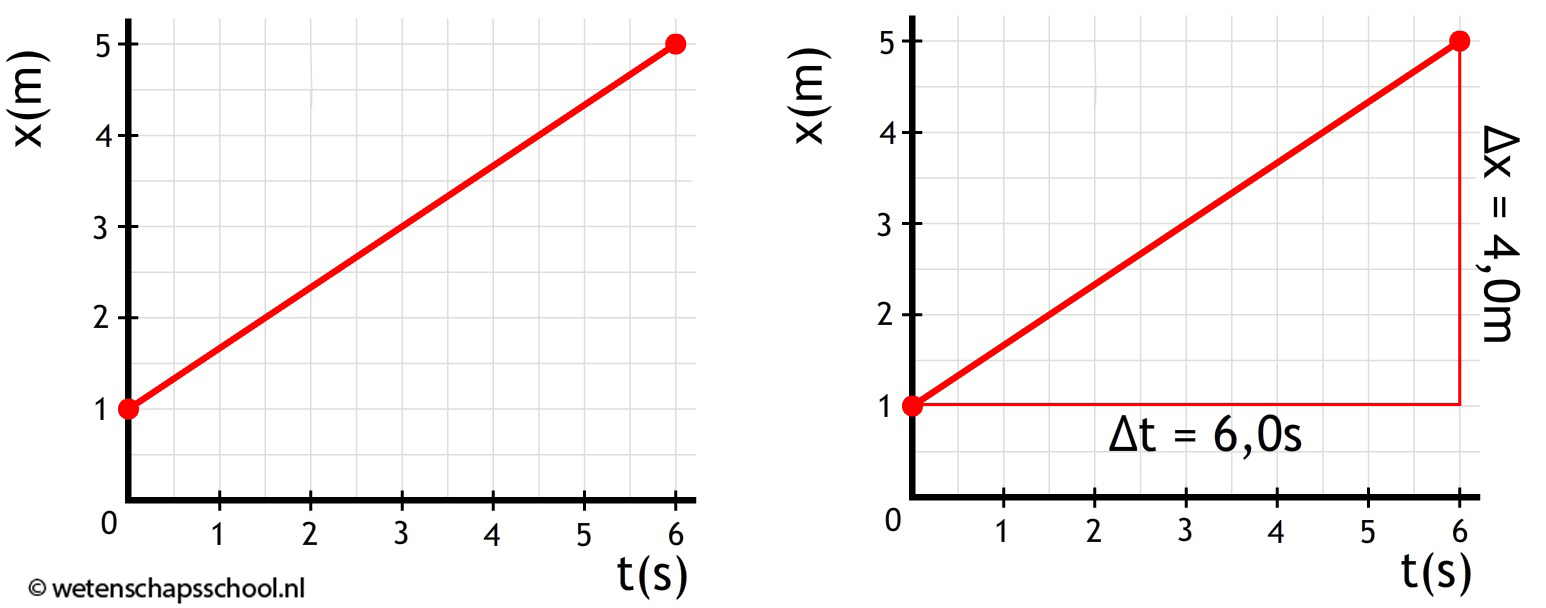
 INSTRUCTIE:
(x,t)-diagram
INSTRUCTIE:
(x,t)-diagram
 Leerdoelen:
Leerdoelen:
|
- Zorg dat je stilstand, constante snelheid, versnelling en vertraging kan weergeven in een (x,t)-diagram, zowel bij vooruit als achteruit bewegen. Er geldt: hoe steiler de grafiek, hoe groter de snelheid.
- Zorg dat je de gemiddelde snelheid kan bepalen met behulp van een (x,t)-diagram.
|
 Opdrachten
Opdrachten
|
-
Ga naar deze opdracht op de website en speel het programma uit.
- (3p) Noteer waar je op moet letten bij het aflezen van een (x,t)-diagram. Hoe herken je stilstand, constante snelheid, versnelling en vertraging?
- (7p) Beschrijf de beweging van de voorwerpen in de volgende (x,t)-diagrammen:
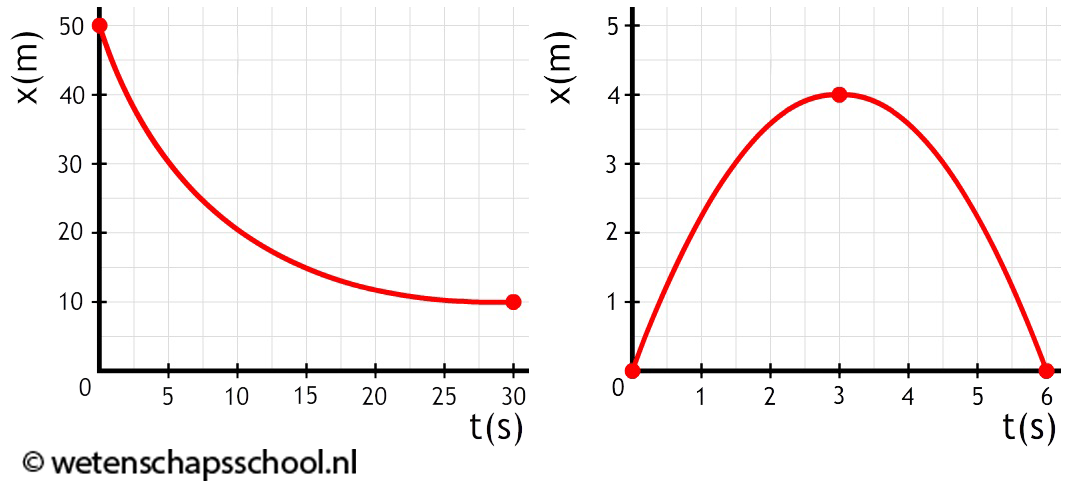
- Schets de volgende (x,t)-diagrammen:
- (2p) Mario rent een tijdje met constante snelheid vooruit. Daarna gaat hij versnellen.
- (2p) Mario staat eerst stil, maar dan gaat hij steeds sneller rennen. Als hij zijn gewenste snelheid bereikt heeft, rent hij met constante snelheid verder.
- (4p) Mario rent even met constante snelheid. Dan gaat hij steeds langzamer rennen tot hij stil staat. Hij rust dan even uit, maar daarna gaat hij weer versnellen.
- (6p) Bereken de snelheid van de voorwerpen die in de volgende (x,t)-diagrammen beschreven zijn.
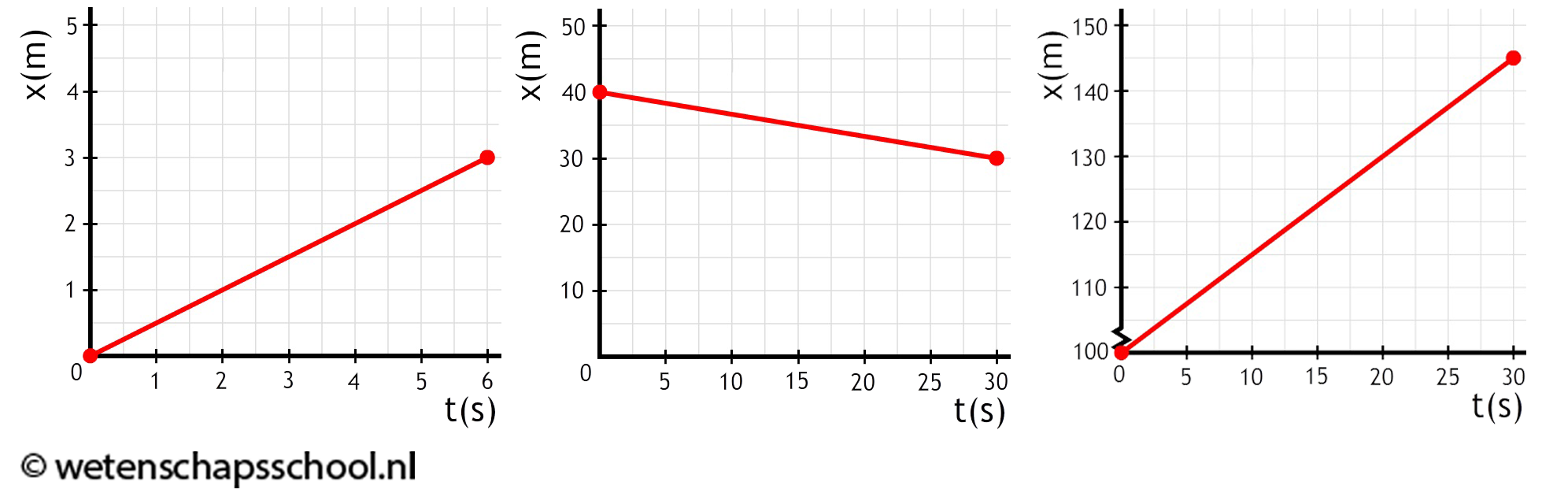
-
Hieronder zien we een (x,t)-diagram waarmee de beweging van een parachutespringer wordt beschreven. De x staat hier voor de hoogte van de springer.
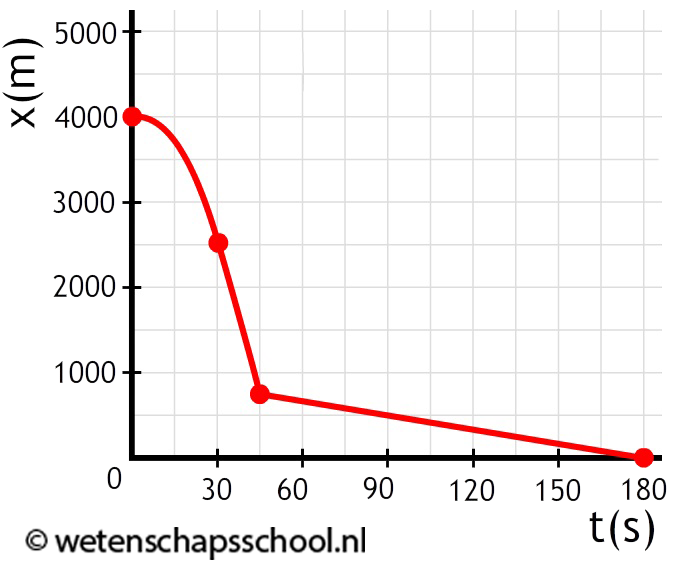
- (1p) Bepaal op welke hoogte de parachute werd geopend. Leg uit hoe je op dit antwoord bent gekomen.
- (1p) Bepaal de beginsnelheid van de springer. Leg uit hoe je op dit antwoord bent gekomen.
- (3p) Bepaal de maximale snelheid die de springer bereikt. Leg uit hoe je op dit antwoord bent gekomen.
-
(3p) Hieronder is een foto gemaakt van een stuiterende pingpongbal met behulp van een stroboscoop. Een stroboscoop is een lamp die met een vaste frequentie lichtflitsen produceert. Als gevolg zie je de bal telkens een stukje verplaatst op de foto. Dit is een goede manier om beweging te bestuderen. Beschrijf de beweging die hier is afgebeeld.

-
In een populaire attractie in een pretpark worden passagiers eerst omhooggetild, waarna ze naar beneden vallen. Aan het eind van de val worden de passagiers afgeremd totdat ze tot stilstand komen. Hieronder zie je een tabel met gegevens van de valbeweging.
| t(s) | x (m) |
| 0,0 | 0 |
| 1,0 | 5 |
| 2,0 | 20 |
| 3,0 | 45 |
| 4,0 | 65 |
| 4,5 | 67 |
| 5,0 | 67 |
- (3p) Zet in het onderstaande diagram alle gegevens uit en teken de grafiek.
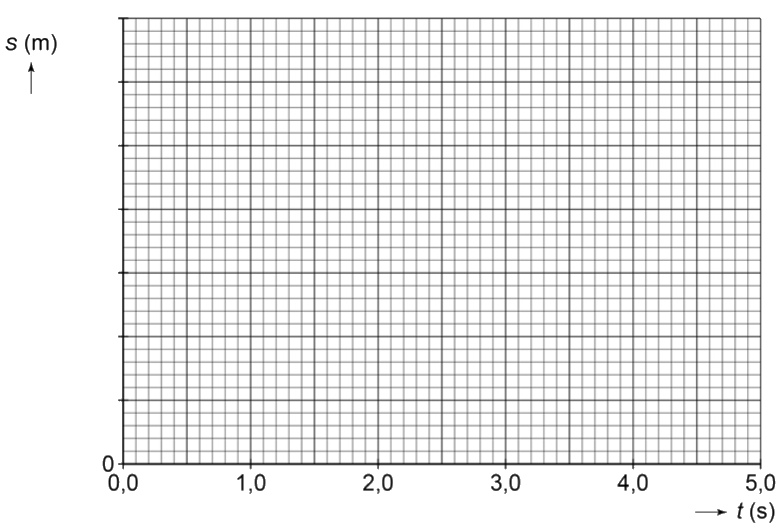
- (1p) Hebben we de eerste drie seconden te maken met stilstand, een constante snelheid, een versnelling of een vertraging?
- (1p) Hebben we in de laatste twee seconden te maken met stilstand, een constante snelheid, een versnelling of een vertraging?
(Bron: Examen VMBO-T, 2022-2)
-
Hieronder zien we een stroboscopische foto van een vallende tennisbal. Een stroboscoop is een lamp die met een vaste frequentie lichtflitsen produceert. Als gevolg zie je de bal telkens een stukje verplaatsten op de foto. Dit is een goede manier om beweging te bestuderen. De stroboscoop maakt 10 flitsen per seconde.
- (1p) Leg aan de hand van de afbeelding uit of een vallende bal versnelt, vertraagt of met een constante snelheid beweegt.
- (1p) Bereken hoeveel tijd er tussen twee lichtflitsen zit.
- (2p) Bepaal hoelang de gehele beweging in de foto geduurd heeft.
- (4p) Maak een (x,t)-diagram van de beweging. Gebruik hiervoor telkens de positie van de onderkant van de tennisbal.

|
§5 Het (v,t)-diagram
In deze paragraaf bespreken we de zogenaamde (v,t)-diagrammen. Ook hiermee kunnen we beweging beschrijven.
Een (v,t)-diagram is een diagram met op de horizontale as de tijd (t) en op de verticale as de snelheid (v). Hieronder zijn een aantal voorbeelden afgebeeld. Links zien we een grafiek waarbij de snelheid van een voorwerp de gehele beweging gelijk is aan 0 m/s. Het voorwerp staat in dit geval dus stil. In de tweede afbeelding zien we een voorwerp waarbij de snelheid de gehele tijd 2,0 m/s blijft. Hier hebben we dus te maken met een constante snelheid.
HIER IMAGES BOOK !!!
Linksonder zien we een diagram waarbij de snelheid van een voorwerp toeneemt. Er is hier dus sprake van een versnelling. Rechts neemt de snelheid juist af. Hier hebben we dus te maken met een vertraging. Let erop dat een vertraging niet betekent dat het voorwerp achteruit gaat. In dit geval gaat het voorwerp vooruit, maar steeds langzamer!
HIER IMAGES BOOK !!!
In al deze (v,t)-diagrammen geldt:
- Hoe hoger de grafiek, hoe groter de snelheid.
Zoals je gemerkt hebt, lees je (x,t)- en (v,t)-diagrammen op een heel andere manier af. In de onderstaande afbeelding is dit nog een keer samengevat:
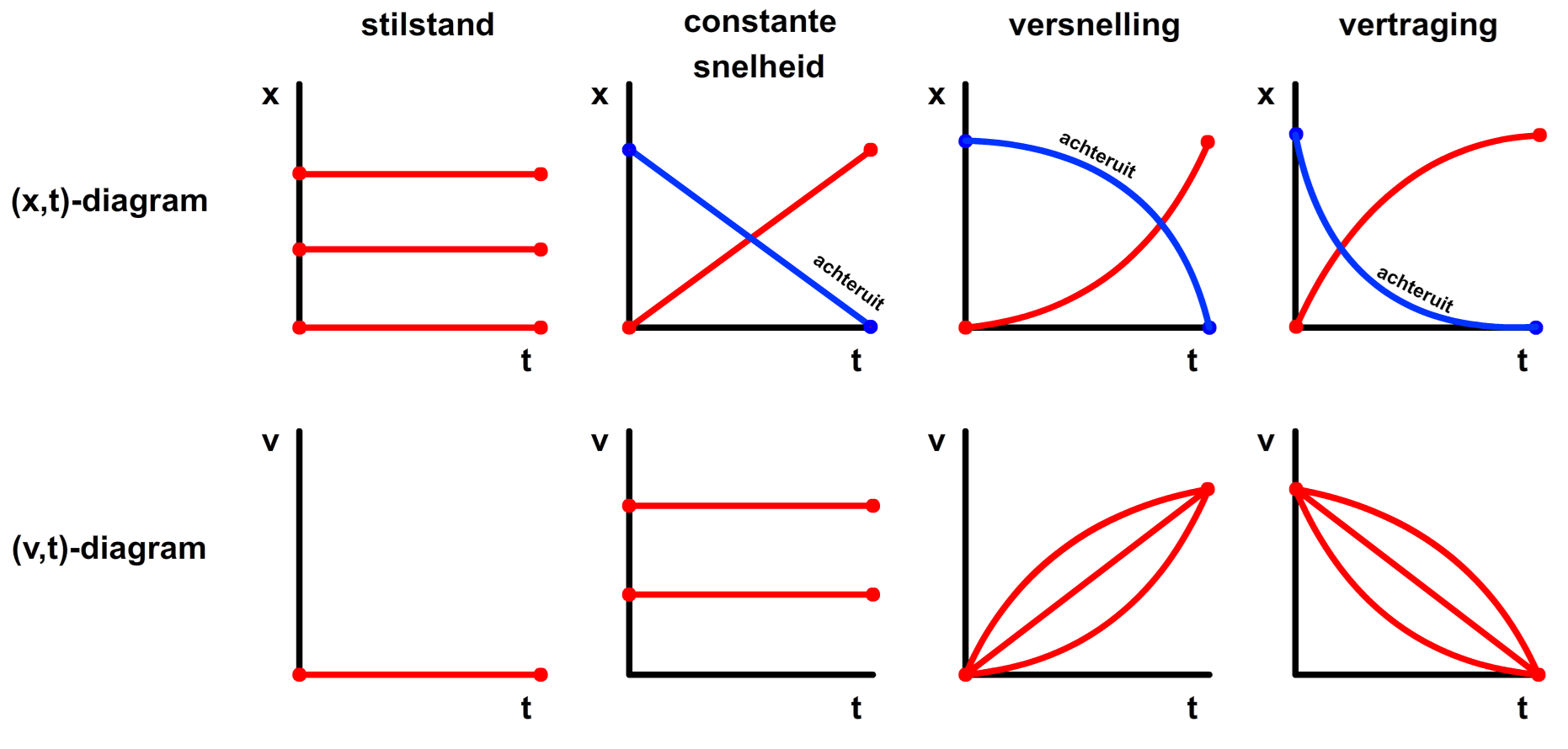
 INSTRUCTIE:
(v,t)-diagram
INSTRUCTIE:
(v,t)-diagram
 Leerdoelen:
Leerdoelen:
|
- Zorg dat je stilstand, constante snelheid, versnelling en vertraging kan weergeven in een (v,t)-diagram. Er geldt: hoe hoger de grafiek, hoe hoger de snelheid.
- Zorg dat je weet dat een dalende (v,t)-grafiek niet wil zeggen dat het voorwerp achteruit gaat. Het voorwerp vertraagt dan vooruit.
|
 Opdrachten
Opdrachten
|
-
Ga naar deze opdracht op de website en speel het programma uit.
Behaal ook hier 15 punten. Let op! Nu zitten (x,t)- en (v,t)-diagrammen door elkaar!
- (3p) Noteer waar je op moet letten bij het aflezen van een (v,t)-diagram. Hoe herken je stilstand, constante snelheid, versnelling en vertraging.
-
(2p) Beschrijf de beweging in de volgende diagrammen. Geef telkens aan of het voorwerp versnelt of vertraagt.
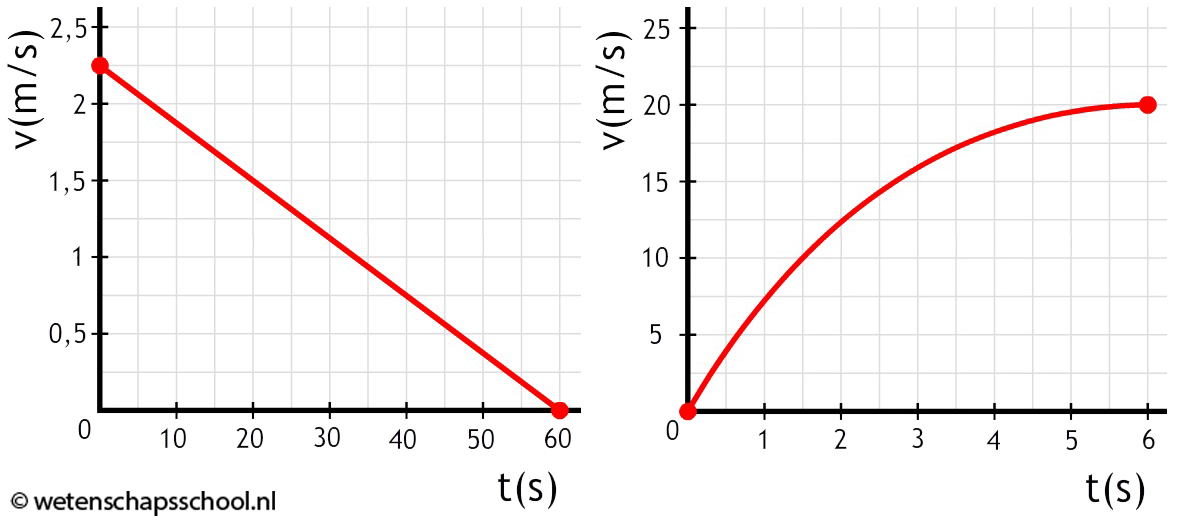
-
Schets de volgende v,t-diagrammen:
- (2p) Mario gaat eerst met constante snelheid vooruit. Dan staat hij stil.
- (2p) Mario begint langzaam te rennen met een constante snelheid. Na een tijdje versnelt hij.
- (2p) Mario begint te rennen met een hoge snelheid, maar zijn snelheid neemt telkens een beetje af. Op een gegeven moment heeft hij een snelheid bereikt waarbij hij goed kan blijven rennen. Vanaf dat moment blijft hij met een constante snelheid rennen.
|
 Stappenplan: Rekenen met snelheid
Stappenplan: Rekenen met snelheid
 Stappenplan: Rekenen met snelheid
Stappenplan: Rekenen met snelheid
 Leerdoelen:
Leerdoelen:
 Opdrachten
Opdrachten
 Voorbeeld
Voorbeeld
 Leerdoelen:
Leerdoelen:
 Opdrachten
Opdrachten

 Leerdoelen:
Leerdoelen:
 Opdrachten
Opdrachten
 Voorbeeld
Voorbeeld
 Voorbeeld
Voorbeeld

 Leerdoelen:
Leerdoelen:
 Opdrachten
Opdrachten

 Leerdoelen:
Leerdoelen:
 Opdrachten
Opdrachten

















