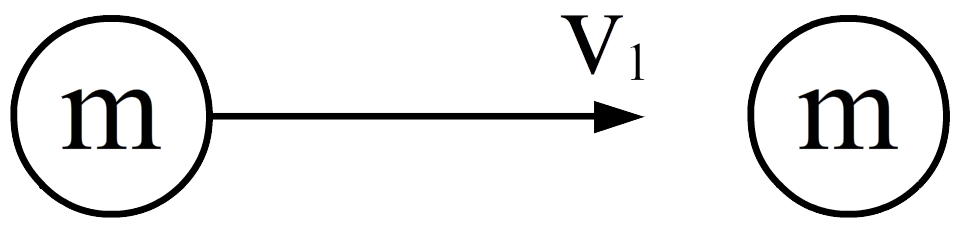Hoofdstuk 7
Deeltjesfysica (keuzemodule VWO)
§1 Impulsbehoud §2 Relativistische impuls en energie §3 Deeltjesfysica
§1 Impulsbehoud
In dit hoofdstuk gaan we het hebben over elementaire deeltjes—de fundamentele bouwstenen van ons universum. Onderzoek naar deze deeltjes vindt met name plaats door ze met snelheden in de buurt van de lichtsnelheid tegen elkaar aan te schieten. Als gevolg hebben we de relativiteitstheorie nodig om deze botsingen goed te beschrijven. In deze paragraaf doen we onderzoek naar botsingen in de klassieke natuurkunde met behulp van het begrip impuls. In de volgende paragraaf gaan we de relativistische versie van de impuls bestuderen en ook de relativistische versie van de energie. We eindigen dit hoofdstuk met een overzicht van de elementaire deeltjes die we tot nu toe hebben gevonden.
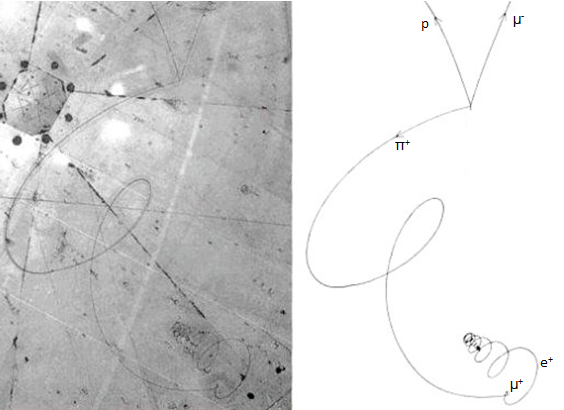
Op verschillende plaatsen op aarde zijn grote deeltjesversnellers gebouwd. Dit zijn lange buizen, waarin kleine deeltjes met behulp van magnetische en elektrische velden versneld worden tot bijna de lichtsnelheid. De bekendste van deze deeltjesversnellers is CERN, te vinden in Zwitserlands (zie de linker onderstaande afbeelding). Dit is een cirkelvormige versneller met een omtrek van wel 27 km! De versnelde deeltjes worden tegen elkaar aangeschoten. Bij deze botsing ontstaan vaak vele deeltjes, die daarna met detectoren waargenomen kunnen worden (zie de rechter afbeelding). Ook bij de detectie worden vaak magneetvelden gebruikt. In het hoofdstuk "Magnetisme" in klas 6 gaan we leren hoe dit werkt.

Als we het botsen van elementaire relativistische deeltjes willen begrijpen, dan is het handig eerst het botsen van alledaagse voorwerpen te bestuderen. Hierbij kunnen we immers gewoon de klassieke natuurkunde gebruiken. In de 17de eeuw kreeg de Franse filosoof René Descartes door dat bij botsingen de zogenaamde impuls (p) behouden blijft. Wat dit betekent gaan we hieronder zien. Laten we beginnen met de definitie van de impuls. Er geldt:
$$p=mv$$
|
In een paar stappen kunnen we afleiden dat bij elke botsing de impuls behouden blijft. We beginnen door de tweede wet van Newton (Fres = ma) in termen van de impuls te schrijven:
$$F_{res} = ma = m \frac{\Delta v}{\Delta t} = \frac{\Delta (mv)}{\Delta t} = \frac{\Delta p}{\Delta t}$$De resulterende kracht is dus gelijk aan de verandering van de impuls in de tijd. Dit is trouwens ook hoe Newton zelf de resulterende kracht beschreef. Nu gaan we deze formule toepassen op de derde wet van Newton. Volgens de derde wet geldt dat als deeltje A een kracht uitoefent op deeltje B, dat dan deeltje B altijd een even grote kracht uitoefent op deeltje A, maar in tegengestelde richting. In formuletaal schrijven we dit als volgt op:
$$ F_{A\rightarrow B} = -F_{B\rightarrow A} $$Als we de nieuwe definitie van de tweede wet hierin invullen, dan vinden we:
$$\frac{\Delta p_{A\rightarrow B}}{\Delta t} = -\frac{\Delta p_{B\rightarrow A}}{\Delta t}$$Als we beide kanten met Δt vermenigvuldigen, dan vinden we:
$$\Delta p_{A\rightarrow B} = -\Delta p_{B\rightarrow A}$$Met Δp = peind - pbegin vinden we:
$$p_{A\rightarrow B,e} - p_{A\rightarrow B,b} = - p_{B\rightarrow A,e} + p_{B\rightarrow A,b}$$Als we de begintermen naar links halen en de eindtermen naar rechts, dan vinden we:
$$p_{A\rightarrow B,b} + p_{B\rightarrow A,b} = p_{A\rightarrow B,e} + p_{B\rightarrow A,e}$$Aan de linkerzijde zien we nu de totale impuls van beide deeltjes aan het begin en aan de rechterzijde zien we de totale impuls van beide deeltjes aan het eind. We kunnen dit dus schrijven als:
$$ p_{tot,b} = p_{tot,e} $$We zien hier dat de totale impuls behouden is in de tijd. We noemen dit de wet van behoud van impuls.
Hieronder gaan we een paar voorbeelden bespreken waarbij we rekenen aan botsingen met behulp van de wet van behoud van impuls. Hierbij is het noodzakelijk onderscheid te maken tussen twee type botsingen. Bij een inelastische botsing blijven de deeltjes na de botsing aan elkaar vastzitten en bewegen ze als één geheel verder. Een voorbeeld is een mug die tegen de voorruit van een auto botst en daarna geplet op het raam met de auto meebeweegt. De andere type botsing is de elastische botsing. Hierbij bewegen de deeltjes na de botsing afzonderlijk van elkaar verder. Denk bijvoorbeeld aan twee biljartballen.
 Voorbeeld
Voorbeeld
|
|
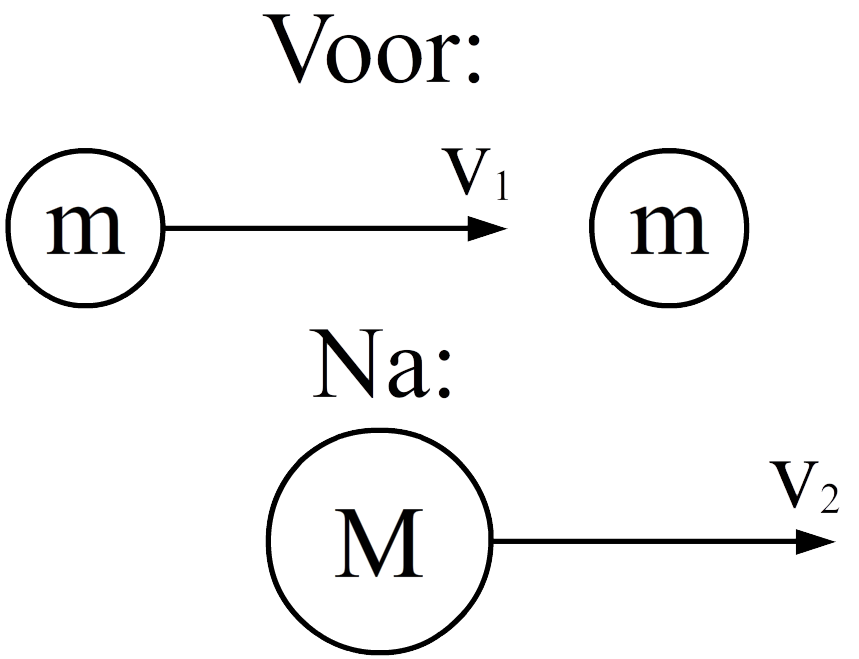
Opdracht: Hieronder zien we twee deeltjes met dezelfde massa die inelastische botsen. Voor de botsing heeft het linker deeltje snelheid v1 en het rechter deeltje staat stil. Na de botsing heeft het gezamelijke deeltje snelheid v2. Vind de relatie tussen snelheid v1 en snelheid v2.
Met impulsbehoud vinden we: $$ p_{links,b} + p_{rechts,b} = p_{e} $$Als we dit uitschrijven met de formule p = mv en uitschrijven dat de massa van het deeltje aan het eind gelijk is aan 2m, dan vinden we: $$mv_1 + m \times 0= Mv_2$$ $$mv_1 = 2mv_2$$Als we aan beide kanten de massa wegstrepen, dan vinden we: $$v_1 = 2v_2$$De snelheid v1 is dus twee keer zo groot als de snelheid v2.
|
 Voorbeeld
Voorbeeld
|
|
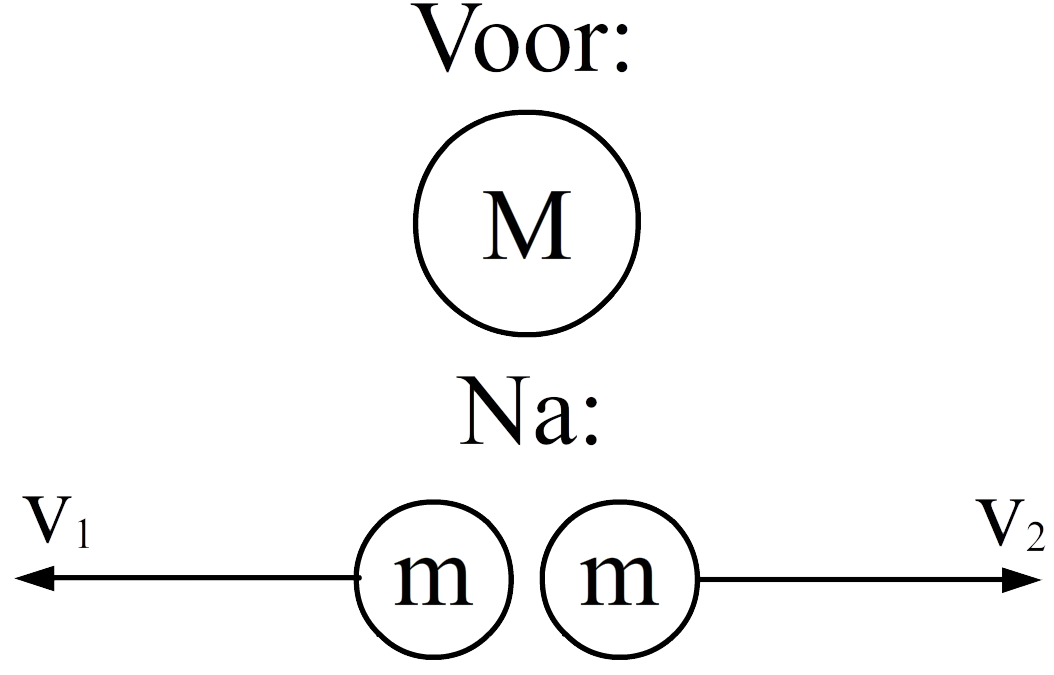
Opdracht: Een deeltje ligt eerst stil en explodeert daarna in twee gelijke delen. Het linker deel beweegt met snelheid v1 en het rechter deel met snelheid v2. Vindt de relatie tussen snelheid v1 en snelheid v2.
Met impulsbehoud vinden we: $$ p_{b} = p_{links,e} + p_{rechts,e} $$De impuls aan het begin is nul, omdat het deeltje eerst stil staat. Met p = mv vinden we: $$ m \times 0 = mv_1 + mv_2$$ $$ 0 = mv_1 + mv_2$$Als we beide zijden delen door de massa, dan vinden we: $$ 0 = v_1 + v_2 $$Dit kunnen we herschrijven tot: $$ v_1 = -v_2$$Aan deze formule kunnen we zien dat beide delen met dezelfde snelheid wegschieten, maar in tegengestelde richting.
|
 Rekenen met impulsbehoud
Rekenen met impulsbehoud
|
|
§2 Relativistische impuls en energie
In deze paragraaf introduceren we de relativistische impuls en de relativistische energie. We gaan de energie daarna gebruiken bij het beschrijven van kernreacties.
Op de website leiden we af dat de relativistische impuls wordt gegeven door:
De wet van behoud van impuls bestaat ook in de relativiteitstheorie, maar de formule voor de impuls is dankzij tijddilatatie en lengtecontractie net iets anders. Er geldt:
$$p = \gamma mv$$
|
De afleiding van deze formule is vrij pittig, maar is voor de liefhebber aan het einde van het hoofdstuk gegeven.
Merkwaardig genoeg volgt uit deze formule dat massa niet behouden is. We tonen dit als volgt aan. Twee deeltjes met gelijke massa botsen inelastisch met een even grote snelheid (v) tegen elkaar aan. De horizontale snelheidscomponent (vx) van de deeltjes komt in de buurt van de lichtsnelheid en de verticale snelheidscomponent (vy) niet (zie de onderstaande afbeelding).
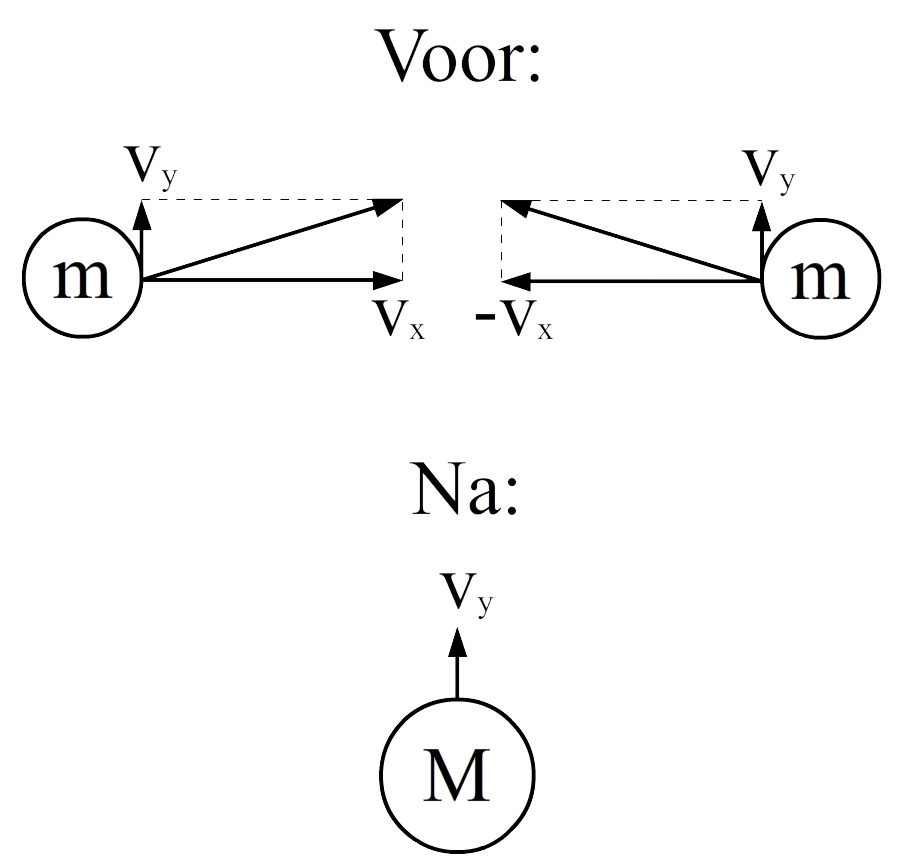
Behoud van impuls in de verticale richting geeft:
$$ \gamma mv_y + \gamma mv_y = Mv_y $$Merk op dat er geen gamma staat aan de rechter zijde van de vergelijking. Dit komt omdat het deeltje na de botsing een erg kleine (niet-relativistische) snelheid heeft. De gamma wordt in dat geval zo goed als 1. We kunnen de formule nog verder versimpelen tot:
$$ 2\gamma mv_y = Mv_y $$ $$ \gamma (2m) = M $$Omdat 2m gelijk is aan de totale beginmassa, kunnen we deze formule ook schrijven als:
$$ \gamma M_{begin} = M_{eind} $$De totale massa is na de botsing dus groter dan voor de botsing! Massa is dus niet behouden! Er is tijdens de botsing massa bijgekomen! Maar hoe is dit mogelijk en waar komt deze massa vandaan? Hiervoor moeten we de relativistische energie bestuderen.
Eerder dit jaar hebben we gezien dat we de formule voor de kinetische energie konden afleiden met behulp van de arbeid (W = Fress). Eerder in dit hoofdstuk hebben we gezien dat we de resulterende kracht kunnen schrijven als Fres = Δp/Δt. Er geldt dus:
$$ W = F_{res}s = \frac{\Delta p}{\Delta t}s $$Eerder in deze paragraaf hebben we gezien dat in de relativiteitstheorie geldt dat p = γmv. De formule voor de arbeid wordt dan:
$$ W = F_{res}s = \frac{\Delta \gamma mv}{\Delta t}s $$Op de website laten we zien dat je deze formule kan uitwerken tot:
In de extra stof aan het eind van het hoofdstuk laten we zien dat de totale energie van een deeltje waar geen krachten op werken in de relativiteitstheorie wordt gegeven door:
$$E = \gamma mc^2$$
|
Als we de gamma uitschrijven, dan vinden we:
$$E = \frac{mc^2}{\sqrt{1-\frac{v^2}{c^2}}}$$Met een wiskundige techniek genaamd de taylorbenadering (die we hier verder niet gaan bespreken), kunnen we deze formule herschrijven tot:
$$E = mc^2 + \frac{1}{2}mv^2 + \frac{3}{8}m\frac{v^4}{c^2} +... $$De tweede term komt als het goed is bekend voor. Dit is de formule voor de kinetische energie, die we ook in de klassieke natuurkunde vinden. De derde term is een relativistische correctie op de kinetische energie. Deze term is bij lage snelheden heel klein, omdat er wordt gedeeld door c2. Totaal nieuw is de eerste term. We noemen dit de rustenergie (E0), omdat deze term zelfs aanwezig is als een voorwerp stilstaat. Voor een voorwerp dat stilstaat versimpelt de bovenstaande formule dus tot:
$$E = E_0 = mc^2 \;\;\;\;\; (v = 0)$$
|
Met de formule voor de rustenergie kunnen we begrijpen wat er gebeurt in situaties waarbij massa niet behouden is. Eerder in deze paragraaf hadden we gevonden dat als twee deeltjes inelastisch botsen, dat dan geldt:
$$ \gamma M_{begin} = M_{eind} $$Als we beide zijden met c2 vermenigvuldigen, dan vinden we:
$$ \gamma M_{begin}c^2 = M_{eind}c^2 $$Met de Taylorbenadering kunnen we de rechter zijde wederom uitschrijven tot:
$$ M_{begin}c^2 + \frac{1}{2}M_{begin}v^2 = M_{eind}c^2 $$ $$ E_{0,b} + E_{kin} = E_{0,e} $$We zien hier dat de kinetische energie aan het begin is verdwenen en dat de rustenergie juist is toegenomen. Omdat de rustenergie afhankelijk is van de massa, moet het dus zijn dat de massa is toegenomen. De kinetische energie is dus "omgezet" in de extra hoeveelheid massa.
Bij nader onderzoek is gebleken dat dit niet betekent dat de individuele protonen, neutronen en elektronen in het voorwerp zwaarder zijn geworden. De kinetische energie is omgezet in warmte en warmte ontstaat doordat de deeltjes van het materiaal harder trillen. Het is deze extra energie die ervoor zorgt dat het voorwerp na de botsing op een weegschaal een hogere waarde aangeeft.
En dit effect treedt niet alleen op bij botsingen. Elke keer als we energie toevoegen aan een object, neemt de massa toe. Een veer wordt bijvoorbeeld (een heel klein beetje) zwaarder als we hem indrukken en een basketbal wordt (een heel klein beetje) zwaarder als we hem roteren. In het dagelijks leven zijn deze effecten echter te klein om te meten. Dit is niet het geval bij radioactief verval. Neem bijvoorbeeld alfaverval. Als we de massa van een atoomkern meten voor het verval en na het verval en we wegen ook het vrijgekomen alfadeeltje mee, dan vinden we dat er een klein beetje massa (en dus wat rustenergie) is verdwenen. Dankzij energiebehoud moet deze energie op een andere manier verschijnen. Dit kan zijn in de vorm van kinetische energie of in de vorm van een foton. In beide gevallen noemen we dit kernenergie.
Neem bijvoorbeeld de volgende vervalreactie:
$$^{32}_{15}P \;\;\;\rightarrow \;\;\; ^{0}_{-1}e \;+\; ^{32}_{16}S$$In tabel 25 van BINAS kunnen we de massa's vinden van verschillende isotopen. Deze massa's geven echter de massa's van de volledige atomen, terwijl we bij kernreacties alleen geïnteresseerd zijn in de atoomkern. Het is daarom nodig om de massa's van de elektronen hier nog van af te halen. De massa van het elektron kunnen we in tabel 7 vinden. We vinden in dit geval de volgende massa's:
$$m_{P-32} = 31,97362\text{ u} - 15 \times 0,00054858\text{ u} = 31,96539\text{ u}$$ $$m_{e} = 0,00054858\text{ u} $$ $$m_{S-32} = 31,97207\text{ u} - 16 \times 0,00054858\text{ u} = 31,96329\text{ u}$$Als we nu de totale massa voor de reactie vergelijken met de totale massa na de reactie, dan vinden we:
$$\Delta m = m_{eind} - m_{begin} $$ $$ \Delta m = m_e + m_{S-32} - m_{P-32} $$ $$ \Delta m = 0,00054858 + 31,96327 - 31,96566 = -0,00155 \text{ u}$$ $$ \Delta m = -0,00155 \times 1,6605389 \times 10^{-27} = -2,57 \times 10^{-30} \text{ kg}$$We kunnen hieruit concluderen dat er inderdaad massa verdwenen is tijdens de kernvervalreactie. We noemen de verdwenen massa het massadefect.
De rustenergie die hierbij hoort is gelijk aan:
$$E_0 = mc^2 $$ $$E_0 = 2,57 \times 10^{-30} \times (2,997925 \times 10^8)^2 = 2,31 \times 10^{-13} \text{ J}$$
 Rekenen met p = γmv en E=γmc2
Rekenen met p = γmv en E=γmc2
| ||
|  Rekenen met massadefect
Rekenen met massadefect
| |
§3 Deeltjesfysica
In deze paragraaf geven we een kort overzicht van de elementaire deeltjes die in deeltjesversnellers gevonden zijn. Tevens gaan we kijken naar de vier fundamentele krachten waaraan deze deeltjes onderhevig zijn
Het universum bestaat uit drie groepen deeltjes, genaamd de quarks, de leptonen en de bosonen. De theorie die de interactie tussen deze deeltjes beschrijft, noemen we het standaardmodel.
Laten we beginnen met de quarks. Door elektronen op protonen en neutronen te schieten, hebben we gevonden dat protonen en neutronen uit kleinere deeltjes bestaan die we quarks noemen. We weten dit doordat elektronen meestal dwars door een proton of een neutron heen vliegen en slechts af en toe worden afgebogen door interactie met een quark (zie de onderstaande afbeelding). Uit onderzoek is gebleken dat zowel het proton als het neutron uit drie quarks bestaan.
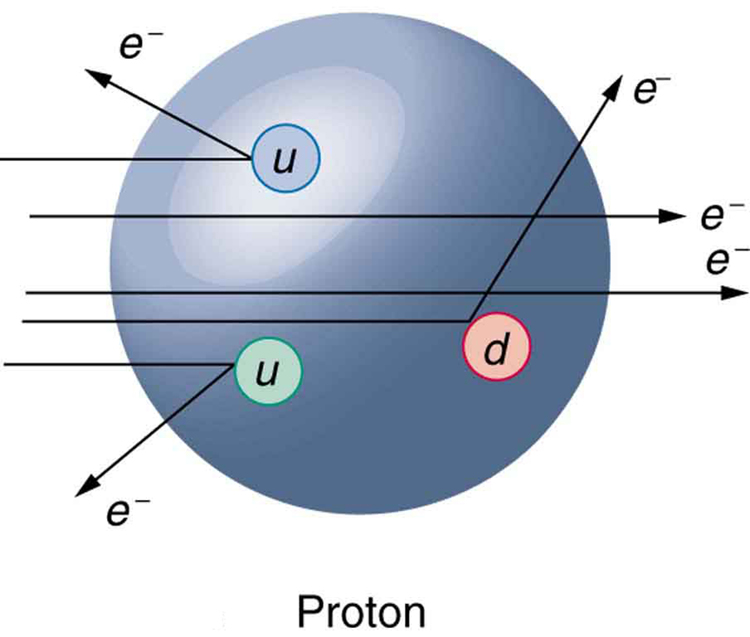
Er bestaan verschillende soorten quarks. De up-quarks (u) hebben een lading van +2/3 e en de down-quarks (d) hebben een lading van -1/3 e. Een proton bestaat uit twee up-quarks en een down-quark (uud) en een neutron uit een up- en twee down-quarks (udd). Als we de ladingen van de quarks bij elkaar optellen, dan vinden we dat het proton zoals gebruikelijk lading +1 heeft en het neutron lading 0.

Ook is ontdekt dat elk deeltje zijn antideeltje heeft. Dit is een deeltje met gelijke massa, maar met een omgekeerde lading. Een voorbeeld dat we al kennen is het positron. Dit is het antideeltje van het elektron. Ook quarks hebben hun antideeltjes. We geven deze deeltjes weer met een horizontale streep boven de letter. Er bestaat dus ook een anti-up-quark (ū) en een anti-down-quark (đ). Een combinatie tussen een quark en een anti-quark noemen we een meson. Hieronder zien we bijvoorbeeld een meson bestaande uit een up-quark (+2/3) en een anti-down-quark (+1/3). De totale lading hiervan is 2/3 + 1/3 = 1.

Om een nog onbekende reden komen quarks alleen in combinaties voor waarbij de totale lading een heel aantal keer de elektronlading (e) is. Dit betekent dat quarks dus niet los voor kunnen komen, want dan zouden ze een lading hebben van +2/3 of -1/3. Als we quarks toch van elkaar los proberen te trekken, dan voegen we via E = mc2 zoveel energie toe dat er weer nieuwe quarks ontstaan. Hieronder kan je bijvoorbeeld zien wat er gebeurt als we een meson uit elkaar trekken.
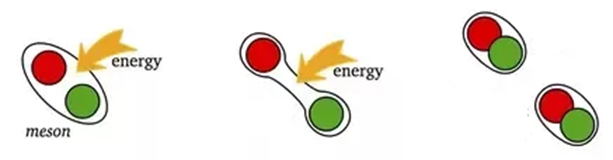
Naast antideeltjes hebben alle quarks ook nog twee zwaardere broertjes die dezelfde lading hebben, maar een grotere massa. Het up-quark heeft als zwaardere broertjes het charm-quark (c) en het top-quark (t). De down-quark heeft als zwaardere broertjes het strange-quark (s) en het bottom-quark (b).
De tweede groep deeltjes waaruit de wereld bestaat, zijn de leptonen. In deze groep behoort het elektron en zijn zwaardere broertjes het muon (μ) en het tauon (τ). Ook de zogenaamde neutrino's (ν) behoren tot deze groep. Neutrino's zijn deeltjes zonder lading en met zo goed als geen massa. Ze zijn dan ook zeer moeilijk te detecteren.
Het neutrino was ontdekt tijdens een studie naar het verval van het neutron in een proton en een elektron. Anders dan we in het hoofdstuk "Radioactiviteit" geleerd hebben, komt er bij deze reactie ook een antineutrino vrij:
$$n \rightarrow p + e^{-} + \bar{\nu}$$Het bestaan van het neutrino werd voorspeld door Pauli. Pauli merkte op dat zowel de energie als de impuls niet behouden leek te zijn bij het verval van het neutron. Hij loste dit op door te postuleren dat er nog een derde deeltje vrij moest komen met de verdwenen impuls en energie. Met erg nauwkeurige detectoren zijn deze deeltjes uiteindelijk inderdaad gevonden.
Dat bij de reactie een antineutrino ontstaat en niet een normaal neutrino, kunnen we afleiden met behulp van het zogenaamde behoud van leptongetal. Alle leptonen hebben een leptongetal gelijk aan 1 en antileptonen hebben een leptopgetal gelijk aan -1. De rest van de deeltjes hebben een leptopgetal van 0. Met een antineutrino aan de rechterzijde van de vergelijking hebben we links een leptongetal van 0 en rechts ook een leptongetal van 1 - 1 = 0.
De laatste groep deeltjes die we gaan bespreken zijn de bosonen. Deze deeltjes zijn verantwoordelijk voor de krachten die op de deeltjes werken. Er bestaan in het universum vier fundamentele krachten. Een van deze fundamentele krachten is de zwaartekracht. Deze kracht wordt beschreven door de algemene relativiteitstheorie. Sommige wetenschappers denken dat de zwaartekracht wordt overgedragen met behulp van deeltjes genaamd gravitonen, maar deze deeltjes zijn nog niet waargenomen. Een tweede fundamentele kracht is de elektromagnetische kracht. Deze kracht wordt veroorzaakt door fotonen. Het foton zorgt voor zowel de afstotende als de aantrekkende krachten die werken tussen geladen deeltjes en ook voor magnetische effecten. Hieronder is bijvoorbeeld schematisch de afstoting van twee elektronen afgebeeld. We noemen een dergelijke afbeelding een Feynmandiagram (vernoemd naar de natuurkundige Richard Feynman, die de heftige natuurkunde achter deze diagrammen heeft beschreven). We lezen dit soort diagrammen van links naar rechts. In dit geval zien we dat twee elektronen naar elkaar toe bewegen, daarna wisselen ze een foton uit en hierdoor bewegen ze weer uit elkaar.
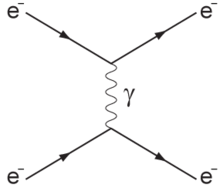
Een ander boson is het gluon. Dit deeltje is verantwoordelijk voor de sterke kernkracht. Dit is de kracht die protonen en neutronen bij elkaar houdt in de kern van atomen. Zonder de kracht zouden protonen direct uit de atoomkern schieten, omdat ze elkaar elektrisch afstoten. Pas als protonen erg dicht op elkaar zitten is de sterke kernkracht groter dan de afstotende elektrische kracht.
Een derde boson is het W-boson. Dit deeltje is verantwoordelijk voor de zwakke kernkracht. Als een down-quark een W--boson uitzendt, dan verandert het in een up-quark. Als een up-quark een W+-boson uitzendt, dan verandert het in een down-quark. Met het W--boson kunnen we iets nauwkeuriger begrijpen wat er gebeurt als een neutron vervalt. Een down-quark zendt een W--boson uit en verandert in een up-quark, waardoor het neutron een proton wordt. Het W--boson valt dan na korte afstand uiteen in een elektron en een neutrino (zie de onderstaande afbeelding. We lezen deze afbeelding van beneden naar boven).
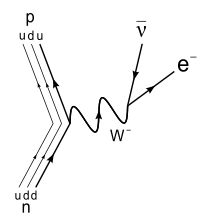
Naast de twee W-bosonen bestaat ook het Z-boson. Dit is een neutraal deeltje dat door verschillende deeltjes uitgezonden kan worden. Een deeltje verandert niet onder uitzending van een Z-boson. Hieronder zien we bijvoorbeeld de vervalvergelijking van een elektron dat een Z-boson uitzendt:
$$ e^- \rightarrow e^- + Z^0 $$Uit sommige experimenten leek te volgen dat W- en Z-bosonen massa moesten hebben, terwijl theoretisch was voorspeld dat dit niet mogelijk was. Dit probleem is opgelost door aan te nemen dat W-bosonen interacteren met het zogenaamde Higgs-boson. Dit deeltjes komt in grote hoeveelheden in het universum voor en remt W-bosonen af, hetgeen het deeltje de illusie van massa geeft. Het bestaan van het Higgs-boson was al decennia lang voorspeld door natuurkundigen, maar werd pas in 2012 gedetecteerd in CERN.
Hieronder is een overzicht te zien van alle deeltjes uit het standaard model die in deze paragraaf besproken zijn. In BINAS tabel 26 is ook een overzicht te vinden. Hier zijn ook de massa's en de ladingen van de deeltjes te vinden. Van elk van de deeltjes in de onderstaande afbeelding bestaat ook nog een anti-deeltje.
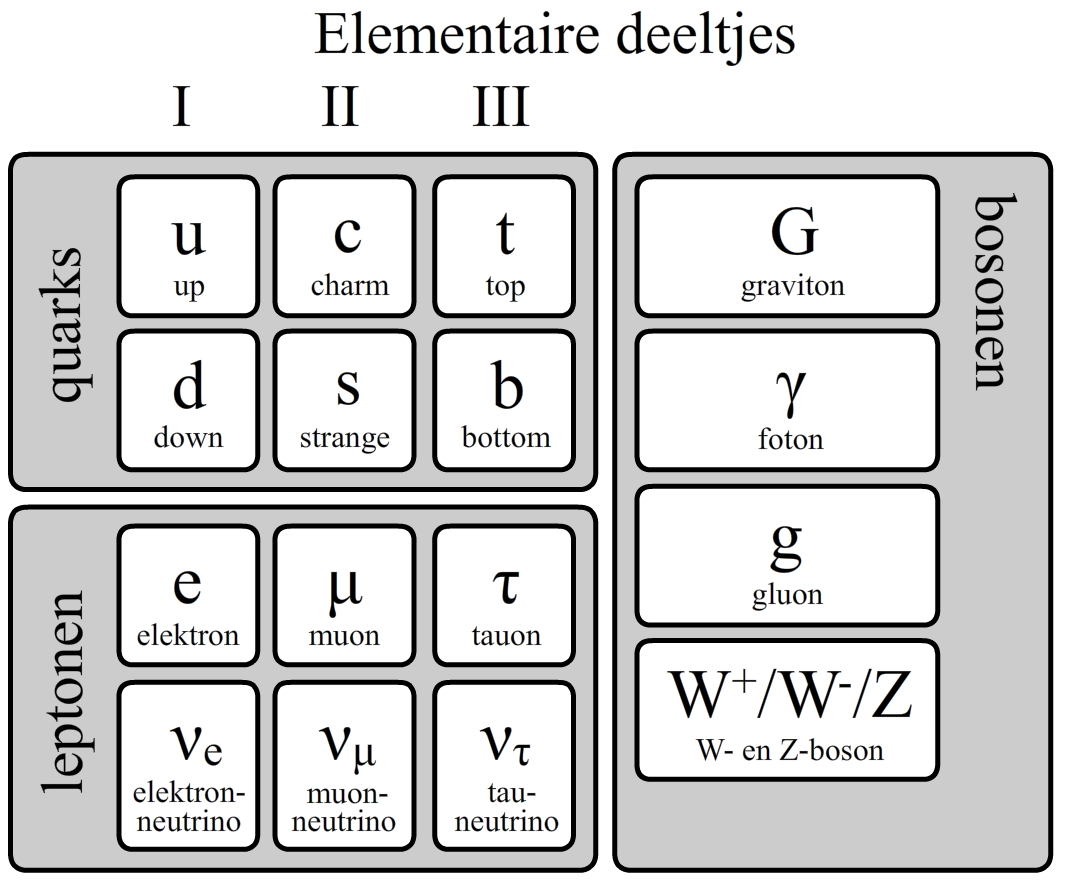
 Redeneren met leptonbehoud en de ladingen van elementaire deeltjes
Redeneren met leptonbehoud en de ladingen van elementaire deeltjes
|
|
 Extra
Extra
|
|
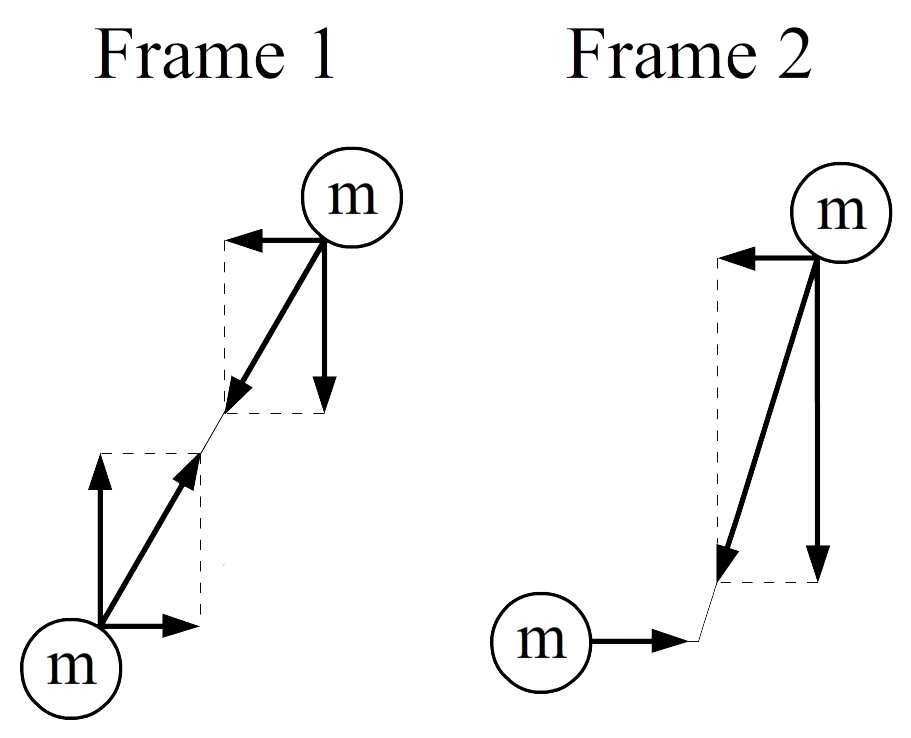
In de onderstaande linker afbeelding zijn twee deeltjes afgebeeld die met dezelfde snelheid tegen elkaar aanbotsen. De snelheid in horizontale richting is voor beide deeltjes erg klein en dus niet relativistisch. De snelheid in de verticale richting is wel relativistisch. Bij een inelastische botsing verwachten we door de gelijke snelheid dat het deeltje na de botsing stil komt te liggen. In de rechter afbeelding bekijken we dezelfde botsing vanuit een stelsel dat verticaal meebeweegt met het linker deeltje. Het linker deeltje lijkt nu alleen naar rechts te bewegen. Omdat we in beide gevallen dezelfde botsing bestuderen, weten we dat het deeltje na de botsing niet zal bewegen in de horizontale richting.
In het rechter voorbeeld, beweegt het linker deeltje niet-relativistisch en het rechter deeltje wel. Voor het rechter deeltje treedt dus tijddilatatie op. Het deeltje zal dus langer doen over de beweging tot aan de botsing (omdat de deeltjes tegelijk botsen, betekent dit dat het rechter deeltje in dit stelsel eerder is vertrokken). Omdat beide deeltjes dezelfde horizontale afstand afleggen en het linker deeltjes meer tijd nodig heeft dankzij de tijddilatatie, vinden we dus dat de horizontale snelheid van het deeltje kleiner moet zijn dan dat van het linker deeltje. Omdat de tijd met een factor γ groter wordt, wordt de horizontale snelheid dus met een factor γ kleiner. Er geldt dus: $$ v_{x,B} = \frac{v_{x,A}}{\gamma} $$In de Newtoniaanse mechanica kunnen we op deze botsing de wet van behoud van impuls toepassen, waarbij we de impuls definiëren als: $$ p = mv $$Voor de rechter afbeelding levert impulsbehoud in de x-richting: $$ mv_{A,x} - mv_{B,x} = 0 $$ $$ mv_{A,x} = mv_{B,x} $$ $$ v_{A,x} = v_{B,x} $$Met vB = vA/γ vinden we echter: $$ v_{A,x} \neq \frac{v_{A,x}}{\gamma} $$De newtoniaanse definitie van de impuls is dus niet behouden in de relativiteitstheorie. De volgende definitie wel werkt wel: $$ p = \gamma mv $$Met impulsbehoud vinden we nu: $$ \gamma mv_{A,x} - \gamma mv_{B,x} = 0 $$De linker γ wordt 1, omdat deeltje A niet relativistisch beweegt. Met vB = vA/γ vinden we hier: $$ mv_{A,x} - \gamma m \frac{v_{A,x}}{\gamma} = 0 $$ $$ v_{A,x} - v_{A,x} = 0 $$ $$ v_{A,x} = v_{A,x} $$De vergelijking klopt nu wel.
|
 Extra
Extra
|
|
De algemene formule voor de arbeid is: $$ W = \int F dx $$Dit kunnen we uitschrijven tot: $$ W = \int \frac{dp}{dt} dx $$ $$ W = \int \frac{d(\gamma mv)}{dt} dx $$ $$ W = \int md(\gamma v) \frac{dx}{dt} $$ $$ W = \int mvd(\gamma v) $$Met de productregel vinden we: $$ W = \int mv(\gamma dv + vd\gamma ) $$Dit kunnen we uitschrijven tot: $$ W = \int m(v\gamma dv + v^2d\gamma ) $$Ook geldt dat: $$ \frac{d\gamma}{dv} = \frac{v}{c^2}\gamma^3 $$Dit kunnen we omschrijven tot $$ dv = \frac{c^2}{v\gamma^3}d\gamma $$Als we dit invullen in de formule voor de arbeid, dan vinden we: $$ W = \int m\left(v\gamma\frac{c^2}{v\gamma^3}d\gamma + v^2d\gamma \right) $$ $$ W = \int m\left(\frac{c^2}{\gamma^2} + v^2\right) d\gamma $$Als we de term tussen haakjes uitwerken, dan versimpelt deze formule tot: $$ W = mc^2 \int d\gamma = \gamma_{e} mc^2 - \gamma_{b} mc^2 $$Dit is het arbeid-energie-theorema in de relativiteitstheorie. We zien hier dat arbeid zorgt voor een toenamen in de energie, waarbij de energie gegeven is door: $$ E = \gamma mc^2 $$
|
| BINAS: | |
| 7 | Massa van proton, neutron en elektron |
| 7 | Atomaire massa-eenheid (u) |
| 25 | Isotopen (atoommassa, type straling en en stralingsenergie per deeltje) |
| 26 | Bouw en structuur van de materie |