Hoofdstuk 4
Zonnestelsel (HAVO)
§1 Het zonnestelsel §2 De planckkromme §3 Spectraalanalyse
§1 Het zonnestelsel
In dit hoofdstuk bestuderen we het zonnestelsel. In deze eerste paragraaf bespreken we de bewijzen die zijn gevonden voor het heliocentrische model (waarbij de aarde om de zon draait). Ook gaan we de maanfasen, de zons- en maansverduistering en de seizoenen begrijpen.
Vroeger werd geloofd dat de aarde zich in het centrum van het heelal bevindt en dat alle hemellichamen om dit centrum heen draaien. Dit wordt het geocentrische wereldbeeld genoemd. In de 16de eeuw vond Copernicus voor het eerst bewijs dat de aarde om de zon heen draait. Dit wordt het heliocentrische wereldbeeld genoemd. Hij bewees dit als volgt. Al eeuwen was bekend dat de planeten vanaf de aarde gezien niet in nette cirkels bewegen. Om de zoveel tijd lijken de planeten voor een korte tijd even achteruit te bewegen (zie de onderstaande afbeelding). Dit fenomeen wordt retrograde beweging genoemd.

In de onderstaande animatie zien we links het heliocentrische model en rechts het veel complexere geocentrische model:
Copernicus liet zien dat deze beweging verklaard kon worden doordat wij de planeten bekijken vanaf een aarde die zelf ook beweegt. Als we de beweging van deze planeet vanaf de zon zouden bekijken, dan zouden we zien dat de planeten simpele cirkelbewegingen maken. In de onderstaande animateIn de animatie op de website is goed te zien hoe het vanaf de aarde gezien kan lijken dat een planeet soms even terugbeweegt. Het blauwe rondje is hier de aarde en het oranje rondje een andere planeet.
Galileo vond nog meer bewijs. Een van zijn belangrijkste ontdekkingen waren de vier manen die om Jupiter draaien (zie de onderstaande afbeelding). Met deze ontdekking bewees hij nogmaals dat niet alles om de aarde draait, zoals in het geocentrische model werd beweerd.

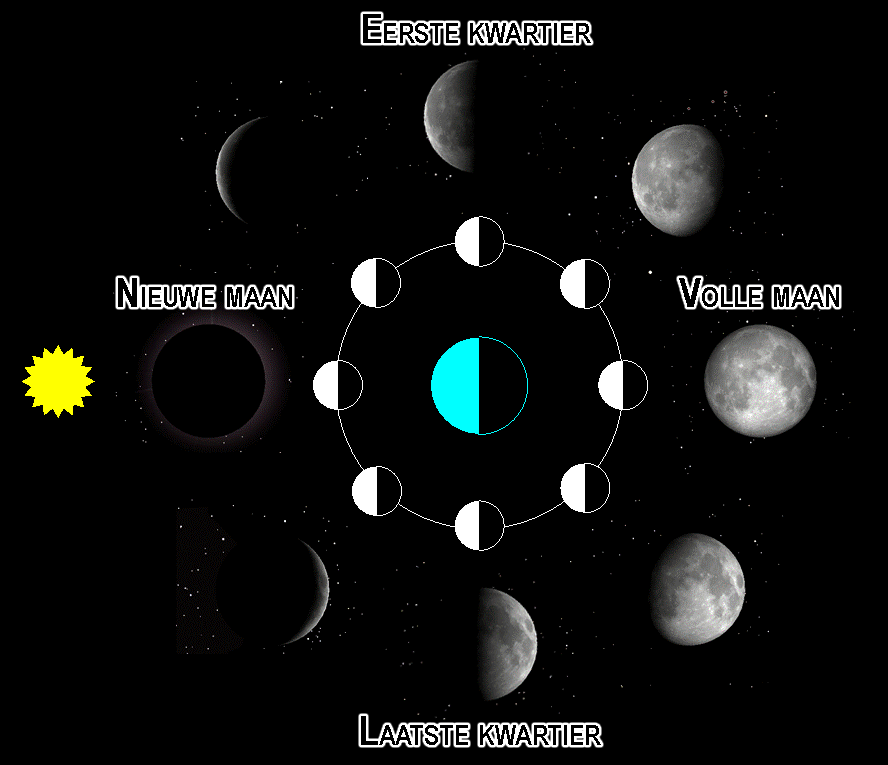
De fasen van de maan kunnen ook goed met het heliocentrische model verklaard worden. In de onderstaande afbeelding zien we de maan in zijn baan om de aarde. Ook zien we de zon die zowel de aarde als de maan verlicht. Aan de donkere kant van de aarde is het nacht en aan de lichte kant is het dag. Doordat de aarde om zijn eigen as draait, wisselen dag en nacht elkaar elke 24 uur af. De maan wordt in zijn baan om de aarde telkens vanaf dezelfde kant verlicht, maar vanaf de aarde gezien is telkens een wisselende hoeveelheid van de donkere en lichte kant te zien.
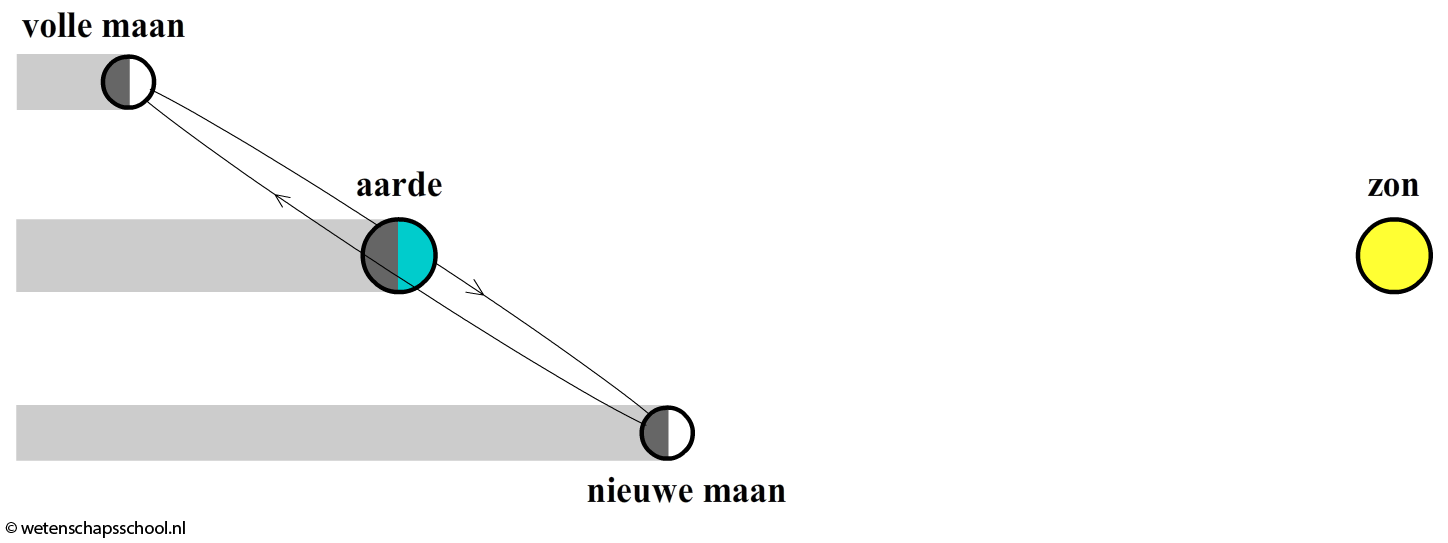
Wellicht dat je je afvraagt hoe we ooit een volle maan zien. Het lijkt in de bovenstaande afbeelding immers dat bij volle maan het licht van de zon geblokkeerd zal worden door de aarde en de maan dus helemaal niet zou bereiken. Dat dit niet het geval is, kunnen we goed zien door de bovenstaande afbeelding eens van de zijkant te bekijken (zie de onderstaande afbeelding). We zien hier dat de baan de maan onder een hoek staat. Als gevolg kan de volle maan het zonlicht toch bereiken.
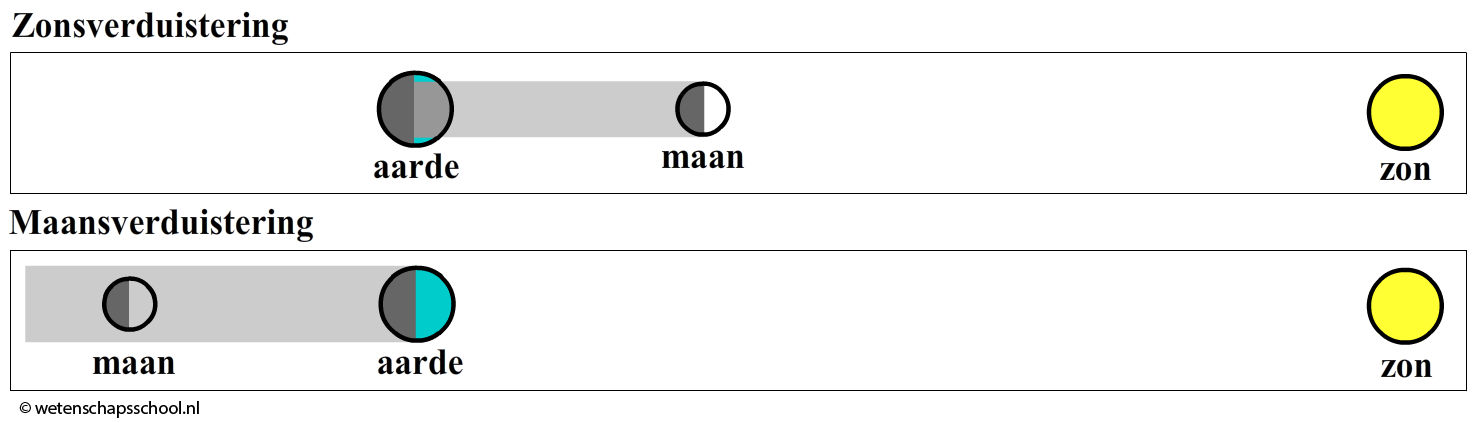
Af en toe staat de maan echter wel precies achter de aarde of tussen de zon en de aarde. Als de maan zich precies tussen de zon en de aarde bevindt, dan vindt een zogenaamde zonsverduistering plaats. Het licht van de zon wordt hier geblokkeerd door de maan. De maan kan ook door de schaduw van de aarde trekken. In dat geval spreken we van een maansverduistering.
In de onderstaande foto zien we een maansverduistering.

In de onderstaande foto's zien we links een zonsverduistering en rechts zien we de schaduw die de maan door de zonsverduistering op de aarde werpt.

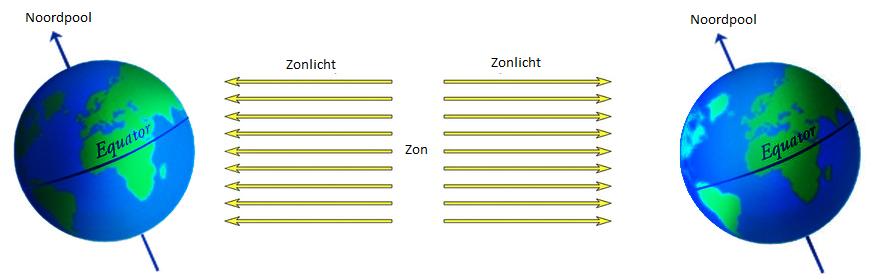
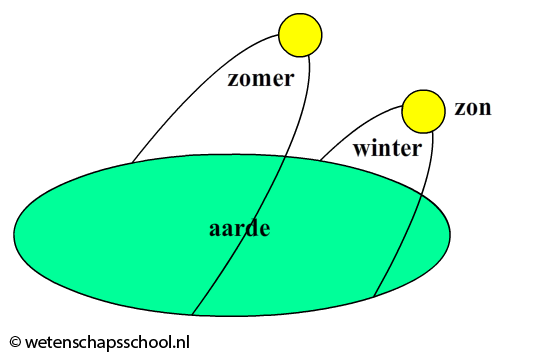
Ook de seizoenen zijn goed te begrijpen in het heliocentrische model. De seizoenen ontstaan doordat de as van de aarde onder een hoek staat. Dit is goed te zien in de onderstaande linker afbeelding. Als de aarde in deze afbeelding links van de zon staat, dan wordt de onderkant van de aarde iets beter verlicht dan de bovenkant. Het is nu in het zuidelijk halfrond zomer en in het noordelijk halfrond winter. Als de aarde rechts van de zon staat, dan wordt de bovenkant iets beter verlicht dan de onderkant. Nu is het juist in het noordelijk halfrond zomer. Vanaf de aarde zien we ditzelfde effect doordat de baan van de zon in de zomer hoger boven de horizon staat. In de rechter afbeelding is dit te zien.
Ons zonnestelsel is zelf ook weer onderdeel van een groter geheel. Onze zon is slechts één ster in een gigantisch melkwegstelsel bestaande uit miljarden sterren. Hieronder is links een foto van zo'n melkwegstelsel te zien. Veel van deze sterren hebben zelf ook weer planeten. We noemen planeten buiten ons eigen zonnestelsel exoplaneten.

In de onderstaande afbeelding zien we een enorme hoeveelheid melkwegstelsels, elk bestaande uit miljarden sterren. Melkwegstelsels die ver van elkaar af staan, bewegen langzaam uit elkaar. Hieruit blijkt dat het heelal steeds groter aan het worden is. We noemen dit ook wel het uitdijen van het heelal. Omdat het heelal steeds groter aan het worden is, moet het dus in het verleden kleiner geweest zijn. Door de snelheid van het uitzetten te achterhalen, is het wetenschappers gelukt om uit te rekenen wanneer het hele heelal zich in één punt bevond. Uit dit punt is het hele heelal ontstaan. We noemen dit de oerknal.

In de opdrachten bij deze paragraaf zal je een aantal eenheden voor afstanden tegenkomen die je in BINAS kan vinden. Afstanden in het zonnestelsel worden vaak gemeten in astronomische eenheden (AE). 1 AE is gelijk aan de afstand van de aarde tot de zon, oftewel 1,49598 × 1011 m. Afstanden tussen sterren worden vaak gemeten in lichtjaar. Dit is de afstand die licht in een jaar aflegt. Deze afstand is gelijk aan 9,461 × 1015 m. Ook deze waarde is te vinden in BINAS.
 Redeneren met het heliocentrische model, met seizoenen en zon- en maansverduisteringen
Redeneren met het heliocentrische model, met seizoenen en zon- en maansverduisteringen
|
|
§2 De planckkromme
Als atomen in een voorwerp trillen, dan zenden ze een heel spectrum aan straling uit. We noemen dit het planckspectrum. In deze paragraaf gaan we leren hoe we met behulp van dit spectrum de temperatuur van de zon en van andere sterren kunnen bepalen.
In het hoofdstuk "Warmte" hebben we geleerd dat atomen in een materiaal met een temperatuur boven de 0 kelvin continu aan het trillen zijn. In dat hoofdstuk hebben we echter niet besproken dat trillende atomen straling uitzenden. Omdat zo goed als elk materiaal een temperatuur heeft boven de 0 K, kunnen we dus stellen dat zo goed als elk materiaal in het universum straling uitzendt. Meestal zit deze straling echter buiten het zichtbare spectrum en kunnen we dit dus niet zien. De aarde en ook wijzelf zenden bijvoorbeeld voornamelijk infraroodstraling uit.
Als de temperatuur van een voorwerp hoog genoeg wordt, dan komt er een moment dat de straling wel zichtbaar wordt. Dit zien we bijvoorbeeld in de onderstaande afbeelding. Een stuk metaal is hier sterk verwarmd en begint hierdoor te gloeien in het rode deel van het spectrum.

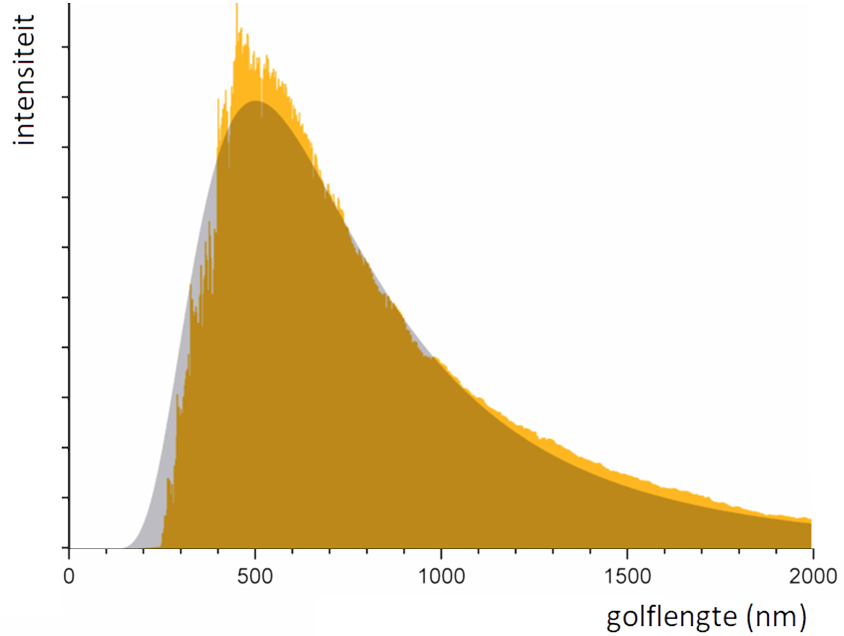
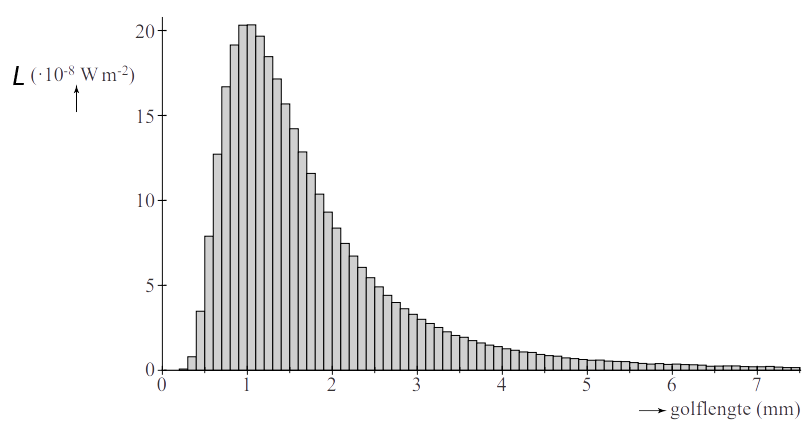
Het licht dat op deze manier ontstaat heeft een karakteristiek stralingsspectrum, genaamd de planckkromme of het planckspectrum. Hieronder is dit spectrum voor een aantal temperaturen weergegeven (op de website wordt dit duidelijker weergegeven met behulp van een animatie). Op de horizontale as staat de golflengte van de straling en op de verticale as de intensiteit van deze straling. De regenboog in het diagram stelt het zichtbare deel van het spectrum voor.
Bij een lage temperatuur zit de straling bijna volledig in het infrarode deel van het spectrum. Als gevolg kunnen we deze straling niet waarnemen met onze ogen. Als de temperatuur hoger wordt, dan komt er een moment dat er genoeg rood licht wordt geproduceerd, zodat we dit met onze ogen kunnen zien. Als we de temperatuur nog meer verhogen, dan komt er een moment dat er in het hele zichtbare spectrum veel licht wordt uitgezonden. Als we alle kleuren licht tegelijk in onze ogen krijgen, dan zien we dit als wit licht. Als de temperatuur nog hoger wordt, dan gaat op een gegeven moment het blauwe licht domineren.
De golflengte van de piek van de planckkromme hangt af van de temperatuur volgens de zogenaamde wet van Wien:
$$\lambda_{max} = \frac{k_w}{T}$$
|
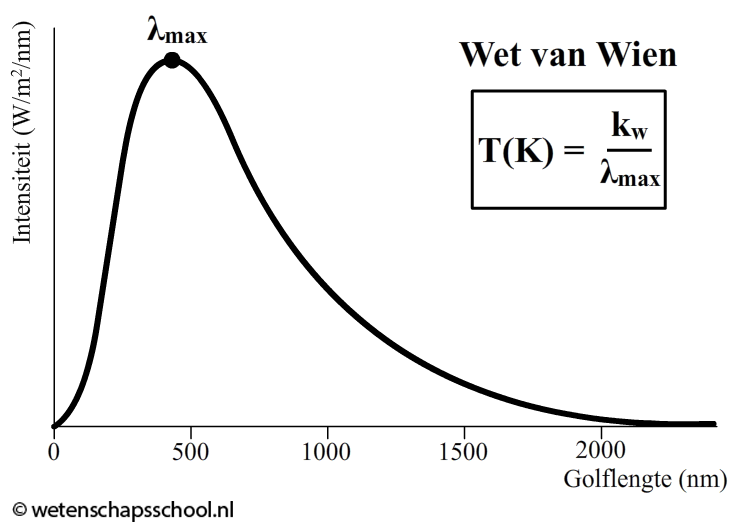
We zien aan deze formule dat hoe meer de piek naar links verplaatst, hoe hoger de temperatuur van het gloeiende voorwerp is. Een blauwe ster heeft dus een hogere temperatuur dan een witte ster en een witter ster heeft een hogere temperatuur dan een rode ster.
De temperatuur moet bij gebruik van de wet van Wien altijd worden gegeven in kelvin. Er geldt:
| $$T(K) = T(^\circ C) + 273$$ |
Met deze formule kunnen we bijvoorbeeld de oppervlaktetemperatuur van de zon berekenen. De piek van het stralingsspectrum van onze zon ligt bij de 500 nm. De oppervlaktetemperatuur is dus:
$$T = \frac{k_w}{\lambda_{max}}$$ $$T = \frac{2,8977721 \times 10^{-3}}{500 \times 10^{-9}} = 5,80 \times 10^3 \text{ K}$$
 Rekenen met de wet van Wien
Rekenen met de wet van Wien
|
|
§3 Spectraalanalyse
In deze paragraaf bestuderen we het licht van de zon en van andere sterren. We kunnen hiermee o.a. achterhalen uit welke stoffen de zon bestaat.
Als we licht van een gloeilamp door een prisma schijnen, dan krijgen we een volledige 'regenboog' aan kleuren te zien. We noemen dit een continu spectrum (zie de onderstaande afbeelding).
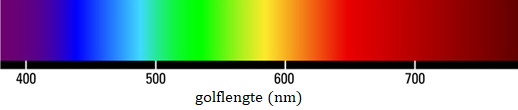
Naast het zichtbare deel van het spectrum, is er ook straling die we met onze ogen niet kunnen zien. Links van het paarse deel van het spectrum bevindt zich bijvoorbeeld ultravioletstraling, röntgenstraling en gammastraling. Rechts van het rode deel van het spectrum hebben we infrarode straling, microgolfstraling en radiostraling. Zoals je in de onderstaande afbeelding kan zien is het zichtbare deel van het spectrum maar een klein deel van het gehele spectrum.
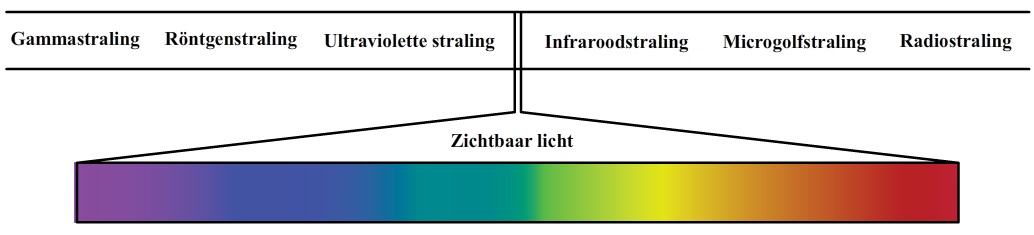
Licht bestaat uit kleine deeltjes die we fotonen noemen. Het verschil tussen verschillende kleuren licht zit hem in de frequentie (f) van de fotonen. Elk foton met een bepaalde frequentie heeft ook zijn eigen fotonenergie (Ef). Deze energie kan als volgt berekend worden:
$$ E_f = hf $$
|
In het hoofdstuk 'trillingen' hebben we gezien dat f = v/λ. Deze formule kunnen we ook toepassen op het foton. Als we voor de snelheid de lichtsnelheid (c) invullen, dan vinden we:
$$E_f = h\frac{c}{\lambda}$$
|
Als we licht van een gloeilamp op waterstof laten schijnen, dan zal het meeste licht hier dwars doorheen schijnen. Alleen licht met specifieke frequenties zal worden geabsorbeerd. Als gevolg worden er in het spectrum van het licht een aantal zwarte lijnen zichtbaar (zie de onderstaande afbeelding). We noemen dit absorptielijnen en het bijbehorende spectrum noemen we een absorptiespectrum.

Het geabsorbeerd licht wordt later in willekeurige richting weer worden uitgezonden door het waterstofgas. Het spectrum van dit licht is hieronder afgebeeld. We noemen dit een emissiespectrum en de lijnen worden spectraallijnen genoemd. Zoals verwacht vinden we in dit spectrum alleen de frequenties die eerder geabsorbeerd waren.

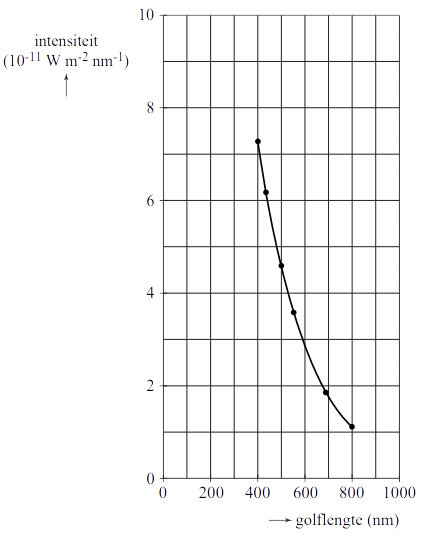
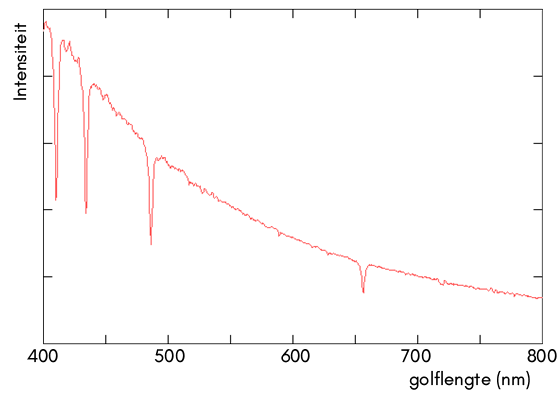
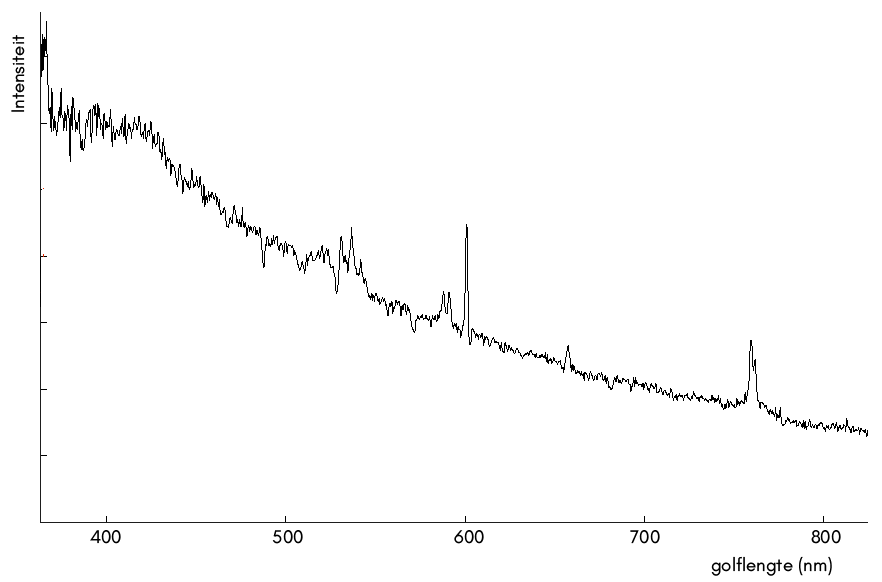
Elke stof heeft zijn eigen unieke spectrum van spectraallijnen. Als gevolg kunnen we aan de hand van het spectrum achterhalen met welke stoffen we te maken hebben. Deze techniek wordt bijvoorbeeld gebruikt om te achterhalen uit welke stof de zon of de sterren bestaan. In de kern van de zon wordt met behulp van kernfusie een continu spectrum aan licht geproduceerd. Als dit licht zich echter door de zon naar buiten werkt, worden een aantal frequenties geabsorbeerd. Hierdoor ontstaan spectraallijnen in het zonnespectrum. We noemen deze lijnen de Fraunhoferlijnen. Hieronder zien we de meest prominente absorptielijnen in het visuele gedeelte van het spectrum van de zon.
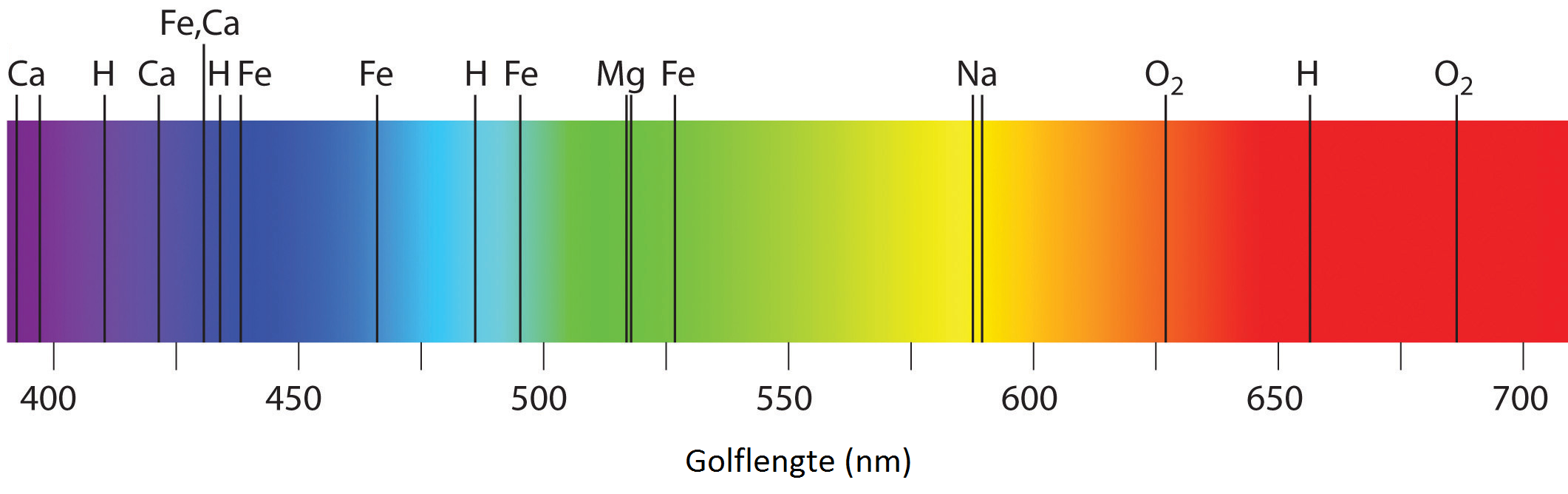
 Zorg dat je kan redeneren over spectra
Zorg dat je kan redeneren over spectra
|
|
| BINAS: | |
| 7 | Constante van Planck, constante van Wien, constante van Stefan-Boltzmann en lichtsnelheid |
| 19A | Het zichtbare spectrum in kleur |
| 19B | Het volledige spectrum |
| 21 | Energieniveaus waterstof (V) |
| 23 | Planck-krommen |
| 31 | Gegevens planeten |
| 32B | Gegevens sterren |
| 32C | Gegevens zon (inclusief astronomische eenheid (AE), vermogen en zonneconstante) |
| 33 | Hertzsprung-Russeldiagram (V) |