Hoofdstuk 6
Relativiteitstheorie (keuzemodule VWO)
§1 Tijddilatatie §2 Lengtecontractie §3 Minkowski-diagrammen
§1 Tijddilatatie
In dit hoofdstuk gaan we het hebben over de speciale relativiteitstheorie van Einstein. In 1905 ontdekte Einstein dat de ruimte en de tijd anders werken dan eerder gedacht werd. In deze paragraaf gaan we leren dat de tijd trager loopt voor voorwerpen die snel voortbewegen. We noemen dit effect tijddilatatie.
In 1905 ontdekte Albert Einstein dat de ruimte en de tijd onlosmakelijk met elkaar verbonden zijn. Voor deze ontdekking dacht men vrij simplistisch over de ruimte en de tijd. Newton zag de ruimte als een gigantische 3-dimensionale diagram waarin objecten geplaatst kunnen worden en de tijd als een universeel tikkende "klok". De waarheid is echter niet zo simpel.
De moderne visie op tijd en ruimte wordt beschreven door de zogenaamde speciale relativiteitstheorie. Deze theorie is gebaseerd op twee aannames. De eerste aanname is het relativiteitsprincipe dat al door Galileo opgesteld is. Galileo had ontdekt dat de natuurwetten in een stilstaande ruimte gelijk waren aan de natuurwetten in een ruimte die rechtlijnig en met een constante snelheid beweegt (we noemen dit ook wel een eenparige beweging). Dit idee is later opgenomen in de eerste wet van Newton. Neem als voorbeeld het vliegtuig. In een eenparig bewegend vliegtuig met gesloten ramen (en zonder turbulentie), is het onmogelijk om te detecteren dat je beweegt. Er is geen enkel experiment dat je binnen dit vliegtuig kan doen waarmee je kan aantonen dat je beweegt. Eenparige beweging en stilstand zijn dus relatieve begrippen.
Einstein voegde aan het relativiteitsprincipe van Galileo nog een tweede aanname toe. In de 19de eeuw ontdekte wetenschappers dat de snelheid van licht voor alle waarnemers dezelfde waarde heeft. De snelheid van het licht is dus een constante en wordt altijd gegeven door:
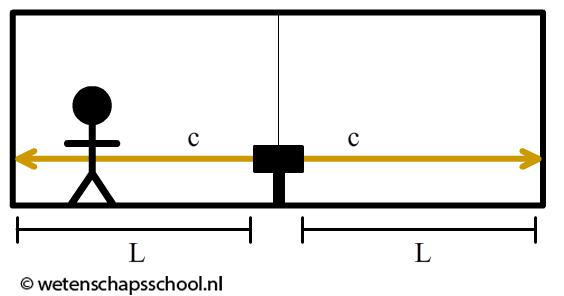
$$ c = 3,0 \times 10^8 \text{ m/s}$$Dit ogenschijnlijk simpele feit heeft grote gevolgen. Laten we een voorbeeld bespreken. In de onderstaande afbeelding zien we een persoon in een ruimteschip. De persoon beweegt mee met het ruimteschip en we zeggen daarom ook wel dat de persoon zich in het referentiestelsel van het ruimteschip bevindt. In het midden van het schip bevindt zich een laser die een lichtdeeltje (een foton) afschiet naar de voor- en achterkant van het schip. Omdat de laser precies in het midden van het schip staat, ziet de persoon in het schip dat de fotonen tegelijk aankomen bij de wanden van het schip.
Nu bekijken we dezelfde situatie door de ogen van een waarnemer die op aarde staat. Terwijl het rechter foton door het ruimteschip beweegt, beweegt het ruimteschip een stukje Δx naar rechts (zie de onderstaande afbeelding). Als gevolg moet het licht een iets langere weg afleggen om de rechter wand te bereiken. In de Newtoniaanse natuurkunde wordt hiervoor gecorrigeerd, doordat een persoon op aarde meet dat het foton met de snelheid van het licht plus de snelheid van het ruimteschip naar rechts beweegt. Het foton legt dus een iets langere afstand af volgens de persoon op aarde, maar doet dit met een iets grotere snelheid, waardoor beide waarnemers het foton op hetzelfde tijdstip tegen de wand zien komen. Eenzelfde soort argument geldt voor het linker foton.
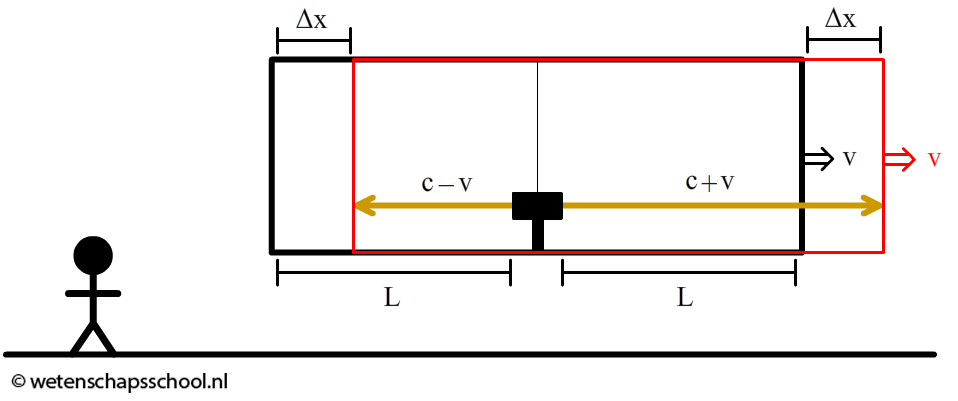
Einstein was het hier niet mee eens, omdat de lichtsnelheid constant is voor alle waarnemers. Ook de persoon op aarde ziet de fotonen dus gewoon met snelheid c voortbewegen (zie de onderstaande afbeelding). Maar als het rechter foton een grotere afstand moet afleggen met dezelfde snelheid, dan duurt het dus langer voordat het foton is aangekomen! Andersom geldt ook dat het linker foton juist eerder aankomt! De persoon in het schip meet dus dat de fotonen tegelijk aankomen, terwijl de persoon op aarde het linker foton eerst ziet aankomen en dan pas het rechter foton. Einstein noemde dit de relativiteit van gelijktijdigheid.
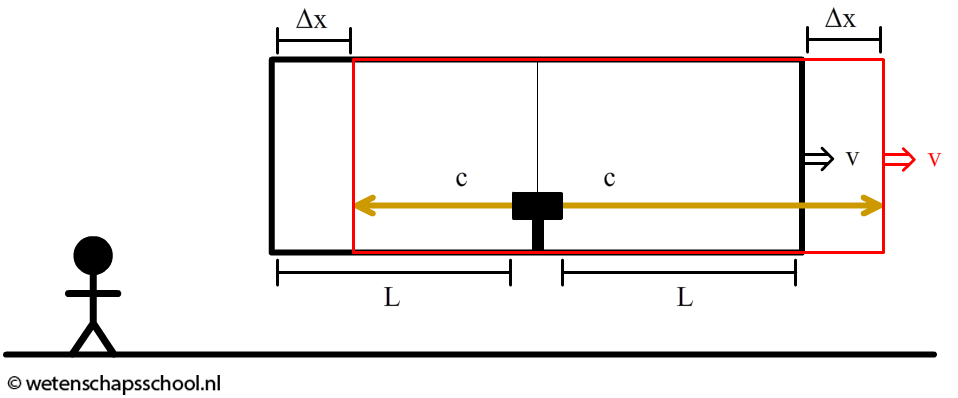
Veel mensen die dit voor het eerst horen, denken dat dit komt doordat de persoon op aarde het schip moeilijker kan meten omdat het in beweging is. Dit is niet wat hier bedoeld wordt. Zelfs met perfecte meetinstrumenten blijft het bovenstaande argument gelden en geldt dus de relativiteit van gelijktijdigheid.
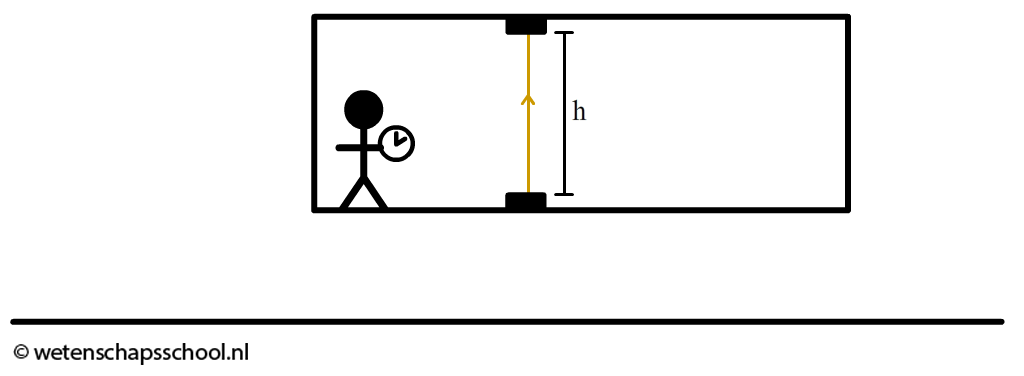
Laten we nog een voorbeeld bestuderen. Een persoon in een ruimteschip kijkt naar een laser die een foton omhoog schiet (zie de onderstaande afbeelding). Het foton komt uiteindelijk terecht in een detector. De afstand tussen de laser en de detector noemen we h. Met de algemene formule Δx = vΔt, vinden we dat voor het foton geldt dat:
$$h = c\Delta t_{eigen}$$Omdat verschillende waarnemers de tijd verschillend meten, moeten we goed bijhouden welke persoon welke gebeurtenis meet. In dit geval bevinden de persoon die de meting verricht en de gebeurtenis die gemeten wordt allebei in hetzelfde stelsel. De gebeurtenis vindt dus plaats in het eigen stelsel van de waarnemer. We spreken bij deze meting daarom van de eigentijd (teigen).
Een tweede persoon bekijkt hetzelfde foton vanaf de aarde. Hij ziet het foton meebewegen met het ruimteschip (zie de volgende afbeelding). Als we de afstand die het licht aflegt Δl noemen, dan vinden we met de stelling van Pythagoras:
$$\Delta l^2 = \Delta x^2 + h^2$$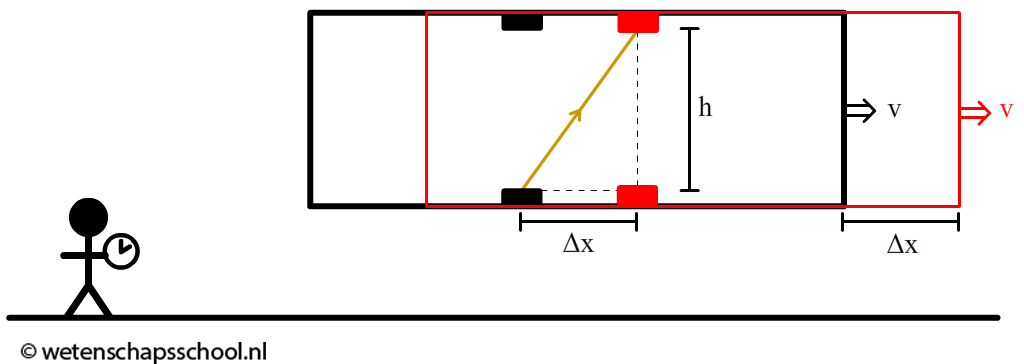
Met de algemene formule Δx = vΔt vinden we dat voor het foton geldt dat Δl = cΔt. Als we dit invullen in de voorgaande formule, dan vinden we:
$$c^2\Delta t^2 = \Delta x^2 + h^2$$Het ruimteschip is tijdens het bewegen van het foton Δx = vΔt verplaatst. Als we dit in de bovenstaande formule substitueren, dan vinden we dat:
$$c^2\Delta t^2 = v^2\Delta t^2 + h^2$$Merk op dat we het hier hebben over de tijd (t) en niet over de eigentijd (teigen). In dit geval meet de waarnemer namelijk de tijd van een fenomeen dat zich in een ander stelsel bevindt. De persoon op aarde meet namelijk de tijd van de bewegende lichtstraal in het ruimteschip.
Eerder hadden we gevonden dat cΔteigen = h. Als we dit in de vorige formule substitueren, dan vinden we:
$$c^2\Delta t^2 = v^2\Delta t^2 + c^2\Delta t_{eigen} ^2$$We kunnen deze vergelijking herschrijven tot:
$$\Delta t^2 (c^2 - v^2) = c^2\Delta t_{eigen} ^2$$Als we delen door c2, dan vinden we:
$$\Delta t^2 \left( 1 - \frac{v^2}{c^2} \right) = \Delta t_{eigen}^2$$Het eindresultaat wordt:
$$\Delta t = \frac{\Delta t_{eigen} }{\sqrt{1-\frac{v^2}{c^2}}}$$
|
Deze formule korten we als volgt af:
| $$\Delta t = \gamma \Delta t_{eigen}$$ $$\gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$$ |
Omdat γ geen eenheid heeft, is het niet nodig de tijdsduren in seconden te meten. De formule geeft ook de juiste antwoorden als je bijvoorbeeld werkt in uren of jaren.
De γ in de formule heeft altijd een waarde groter of gelijk aan 1 en als gevolg vinden we dat Δteigen altijd kleiner is dan Δt. Voor de persoon in het ruimteschip is er dus minder tijd voorbij gegaan tijdens de beweging van het foton. De tijd in het ruimteschip loopt dus slomer. We noemen dit tijddilatatie. Ook tijd is dus relatief!
In het dagelijks leven merken we weinig van tijdsdilatatie. Dit komt omdat de snelheden van voorwerpen in het dagelijks leven veel kleiner zijn dan de lichtsnelheid (v << c). In dat geval ligt v2/c2 erg dicht bij 0 en vinden we:
$$\gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} \approx 1 \;\;\;\;\;\; \text{(v << c)}$$De formule voor de tijddilatatie wordt dan simpelweg Δt = Δteigen. De tijd wordt nu dus door beide waarnemers gelijk gemeten. In deze situatie kunnen we daarom gewoon de traditionele niet-relativistische natuurkunde gebruiken om de wereld te beschrijven. Bij grote snelheden wordt de toevoeging van Einstein echter belangrijk.
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§2 Lengtecontractie
In deze paragraaf gaan we zien dat ook de lengte van voorwerpen verschillend is voor verschillende waarnemers. Dit effect wordt lengtecontractie genoemd.
Tijd is dus relatief. Maar hoe zit het met de ruimte? Om dit te begrijpen, bestuderen we een bekend voorbeeld. Als protonen van de zon op de atmosfeer van de aarde botsen, dan ontstaan deeltjes die we muonen noemen. Deze muonen bewegen dan met een gigantische snelheid naar het aardoppervlak (v = 0,999c), waar we ze kunnen meten. We kunnen deze muonen ook zelf maken in het lab. Als we op aarde een stilstaand muon meten, dan blijkt dit deeltje een gemiddelde levensduur van 2,2 μs te hebben. Na deze periode vervalt het muon in andere deeltjes. Als we met de oude natuurkunde zouden uitrekenen hoe ver het bewegende muon door de atmosfeer zou kunnen reizen, dan vinden we met vΔt = Δx:
$$\Delta x = v\Delta t = 0,999c \times 2,2 \times 10^{-6} = 0,66 \text{ km}$$Het muon kan dus slechts 0,66 km bewegen, maar de atmosfeer is ongeveer 15 km dik! Volgens deze berekening zou het muon dus nooit het aardoppervlak kunnen bereiken! Maar hoe kan het dan dat we de muonen toch kunnen meten? Dit komt omdat we geen rekening hebben gehouden met tijddilatatie. De 2,2 μs vervaltijd geldt voor een muon dat stilstaat in het lab. Dit is dus de eigentijdsduur Δteigen van het muon. Voor het bewegende muon hebben we echter Δt nodig:
$$\Delta t = \frac{\Delta t_{eigen} }{\sqrt{1-\frac{v^2}{c^2}}}$$ $$\Delta t = \frac{2,2 \times 10^{-6}}{\sqrt{1-0,999^2}} = 49 \text{ }\mu\text{s}$$In 49 μs kan het muon de volgende afstand afleggen:
$$0,999c \times 49 \times 10^{-6} = 15 \text{ km}$$Dit is genoeg om het aardoppervlak te bereiken!
Nu bekijken we dezelfde gebeurtenis meereizend met het muon. Als we meereizen met het muon, dan zitten we in hetzelfde stelsel als het muon. Er geldt in dat geval gewoon Δteigen = 2,2 μs! We hadden al berekend dat het muon met deze vervaltijd slechts 0,66 km kan afleggen! Toch weten we dat het muon het aardoppervlak kan bereiken. Hoe is dit mogelijk? Einstein zag maar één uitweg. Voor het muon is de atmosfeer veel dunner. Meereizend met het muon is de atmosfeer van 15 km gekrompen tot slechts 0,66 km! We noemen dit lengtecontractie.
De persoon op aarde meet dus dat het muon de aarde kan bereiken dankzij tijddilatatie. De persoon meereizend met het muon denkt dat het muon de aarde kan bereiken dankzij lengtecontractie. Wat de een ziet als het verslomen van de tijd, ziet de ander als het krimpen van de ruimte. Ruimte en tijd zijn dus onlosmakelijk met elkaar verweven.
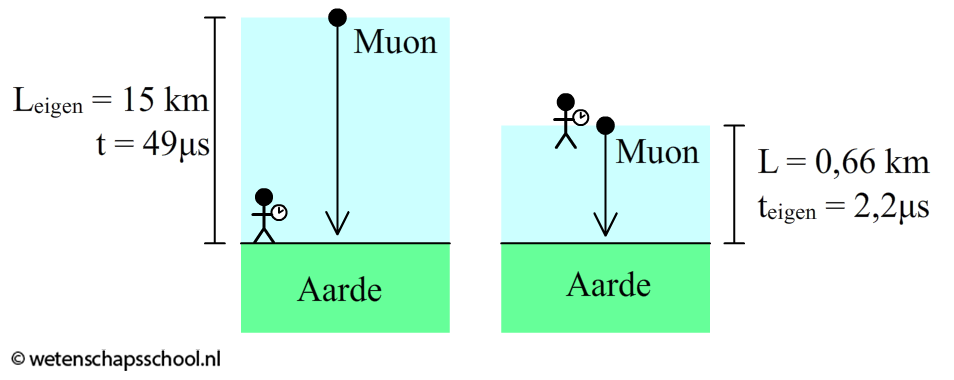
Ook voor de lengtecontractie kunnen we een formule afleiden. Ook hier moeten we verschil maken tussen de lengte (L) en de eigenlengte (Leigen). In dit geval is de relevante lengte de atmosfeer en deze staat in het stelsel van de persoon op aarde. Voor de persoon op aarde heeft de atmosfeer dus lengte Leigen. Voor de persoon meereizend met het muon heeft de atmosfeer lengte L. Er geldt dus:
$$\Delta t = L_{eigen} / v \;\;\;\;\;\; \text{meting vanaf aarde}$$ $$\Delta t_{eigen} = L / v \;\;\;\;\;\; \text{meting vanaf muon}$$Als we beide formules in de tijddilatatieformule (Δt = γΔteigen ) substitueren, dan vinden we:
$$L_{eigen} = \gamma L$$
|
Omdat γ altijd groter of gelijk is aan 1, vinden we dat bewegende voorwerpen kleiner zijn.
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§3 Minkowski-diagrammen
In deze paragraaf gaan we tijddilatatie en lengtecontractie ook met behulp van diagrammen weergegeven. We noemen deze diagrammen Minkowski-diagrammen
In de speciale relativiteitstheorie geven we gebeurtenissen grafisch weer met behulp van ruimtetijd-diagrammen. Dit worden ook wel Minkowski-diagrammen genoemd. Deze diagrammen hebben op de horizontale as de afstand (x) staan en op de verticale as de tijd vermenigvuldigd met de lichtsnelheid (ct). Het voordeel van dit type diagram is dat voorwerpen die met de lichtsnelheid gaan nu altijd een hoek van 45 graden maken met de x-as. Dit kunnen we goed zien als we de formule v = Δx/Δt omschrijven door de teller en de noemer met c te vermenigvuldigen:
$$v = \frac{c\Delta x}{c\Delta t} $$Dan tillen we de c in de teller naar de rechterkant:
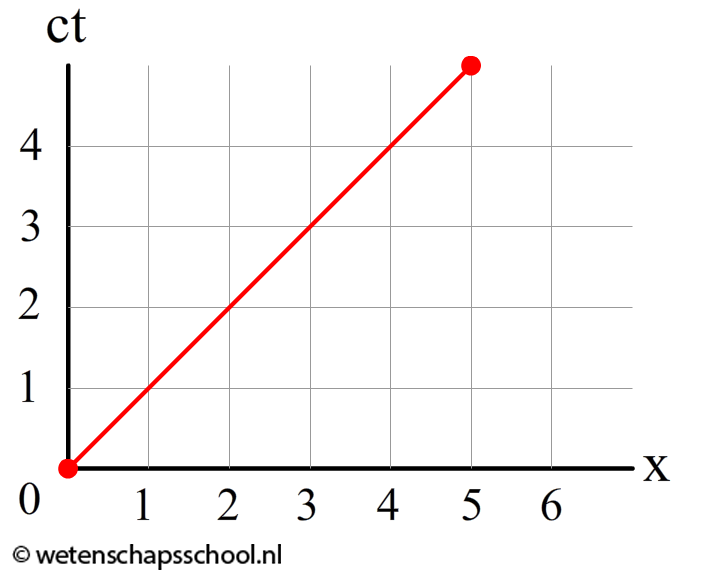
$$v = \frac{\Delta x}{c\Delta t} c$$Neem nu de onderstaande grafiek. Er wordt Δx = 5 meter afgelegd in cΔt = 5 meter. Als we dit invullen in de bovenstaande formule, dan vinden we:
$$v = \frac{5}{5}c = c$$Een grafiek onder een hoek van 45 graden geeft dus inderdaad de lichtsnelheid.
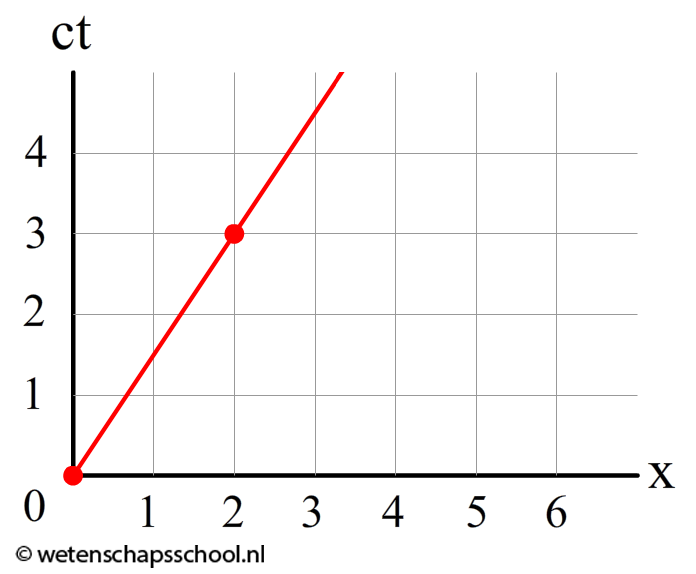
Hieronder zien we een grafiek behorende bij een voorwerp dat niet met de lichtsnelheid beweegt. Ook nu kunnen we de snelheid met dezelfde formule uitrekenen:
$$v = \frac{\Delta x}{c\Delta t} c = \frac{2}{3}c = 0,67 c$$Dit voorwerp beweegt dus met 67% van de lichtsnelheid.
Nu wordt het tijd om weer verschillende stelsels met elkaar te vergelijken. Wederom beginnen we met de oude natuurkunde. In de linker onderstaande diagram zien we een waarnemer A die stil staat. We zien dat deze waarnemer stil staat omdat zijn positie hetzelfde blijft als de tijd voorbij gaat. In het diagram zien we ook een waarnemer B die met een constante snelheid naar rechts beweegt in een ruimteschip met 0,67c.
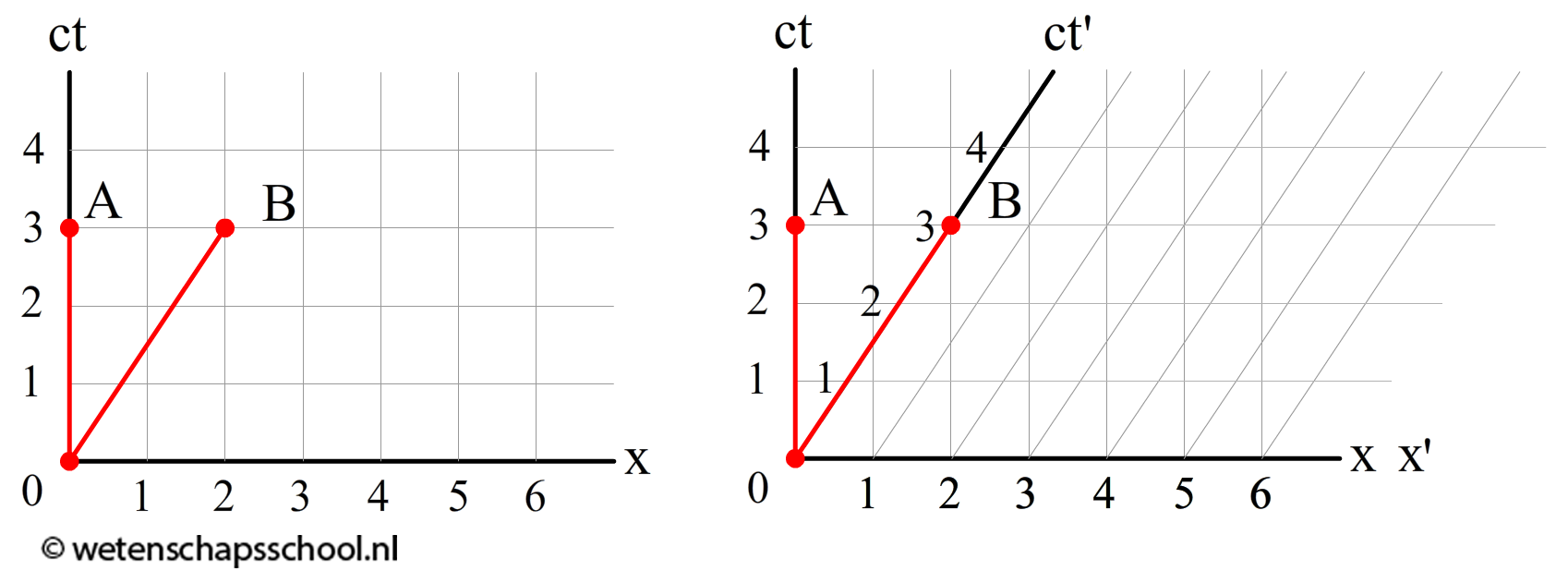
Dankzij het relativiteitsprincipe hadden we echter net zo goed aan kunnen nemen dat juist persoon B stilstaat en persoon A aan het bewegen is. In de rechter afbeelding hebben we het diagram toegevoegd waarin persoon B stilstaat. Om onderscheid te maken tussen het stelsel van A en B, hebben we bij de assen van stelsel B een accent (') gezet. Merk op dat de ct'-as in dit geval schuin loopt. In dit stelsel zien we inderdaad dat de positie x' van persoon B nul blijft als de tijd t' voorbij gaat.
Nu passen we de correctie van Einsteins speciale relativiteitstheorie toe. Een persoon op aarde ziet de tijd in het schip langzamer voorbij gaan dankzij tijddilatatie. We vinden in dit geval de volgende γ-factor:
$$\gamma = \frac{1}{\sqrt{1-\frac{(2/3c)^2}{c^2}}} = \frac{1}{\sqrt{1-(2/3)^2}} = 1,34$$Als er één seconde in het schip voorbij is gegaan, dan is er dus 1,34 seconde voorbij gegaan op aarde. In het onderstaande diagram is dit toegevoegd:
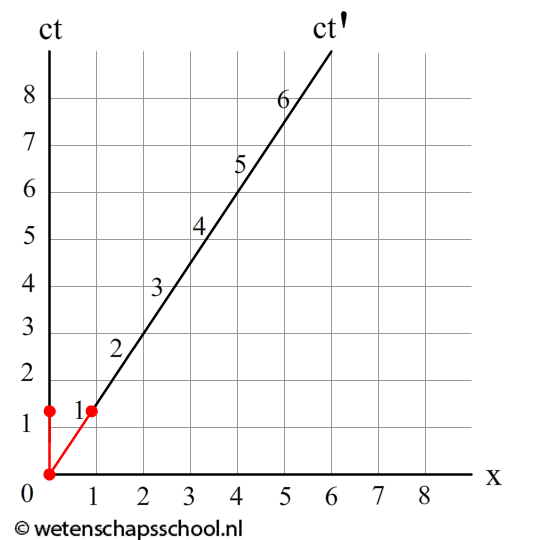
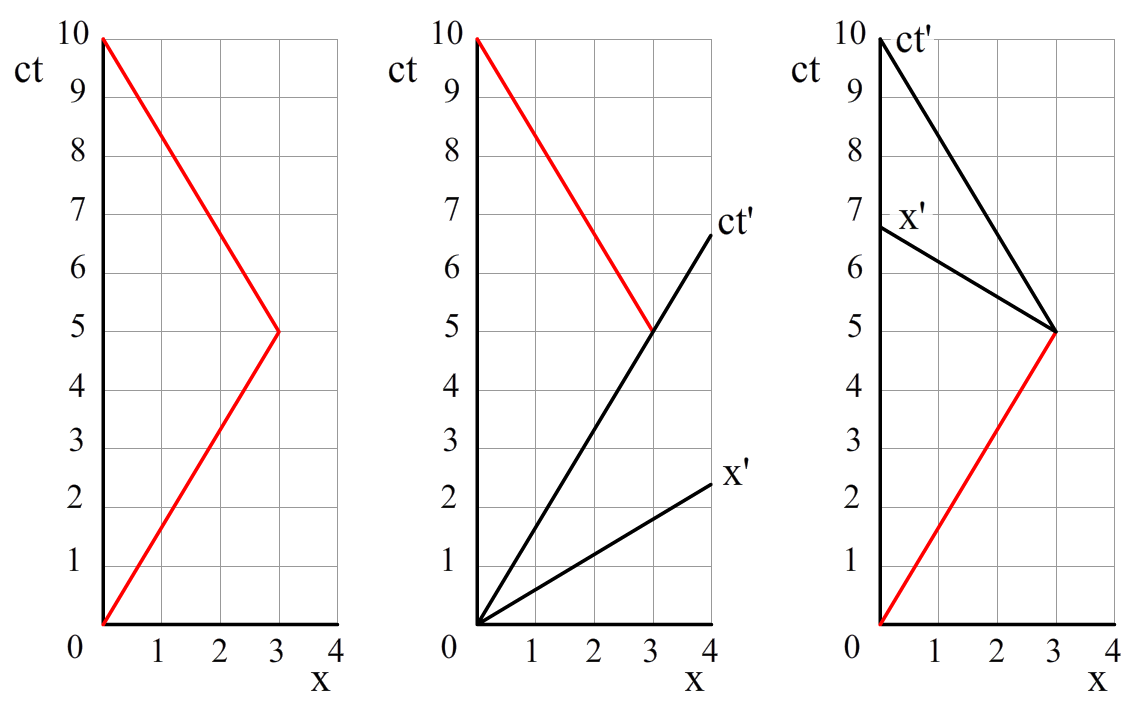
We zijn hiermee echter nog niet klaar. Om het diagram compleet te maken, voeren we het volgende gedachtenexperiment uit. Een persoon in het schip schiet op tijdstip ct' = -3 m, -2 m en -1 m een lichtstraal af naar rechts (zie het linker onderstaande diagram). Wederom worden de lichtstralen gekenmerkt door de hoek van 45 graden met de x-as. Op tijdstip ct' = 0 m reflecteert de persoon de lichtstralen met een spiegel, waarna ze weer terug naar links gaan. Zoals je ziet vindt de persoon in het schip dat de lichtstralen zijn gereflecteerd op dat x'-as op afstand 1, 2 en 3 meter.
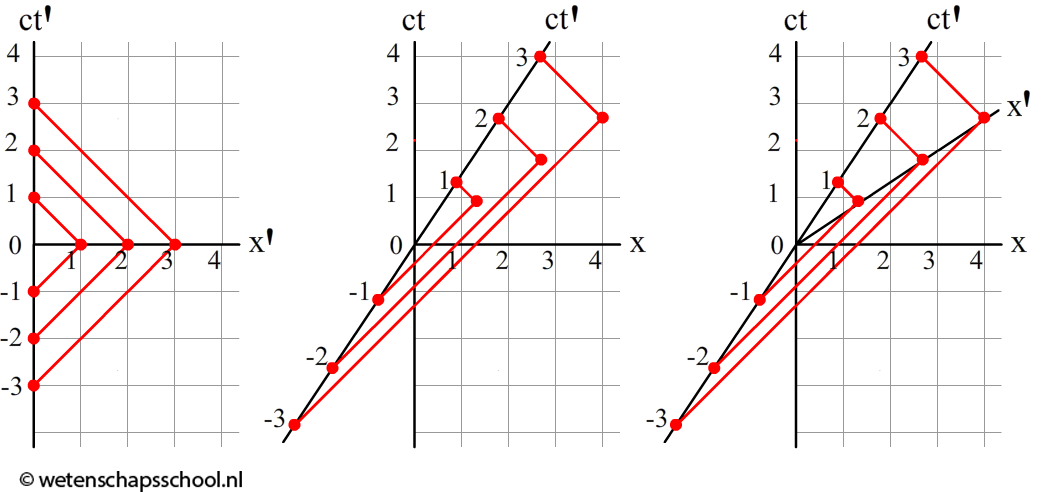
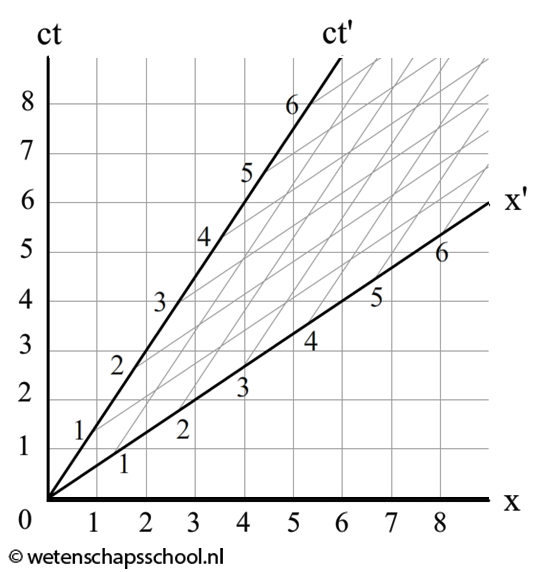
In het middelste diagram zien we dezelfde situatie gezien vanaf de aarde. Wederom starten de lichtstralen op ct' = -3 m, -2 m en -1 m en komen de lichtstralen terug op tijdstip ct' = 1 m, 2 m en 3 m (zie de middelste afbeelding). Omdat we wederom de lichtstralen onder een hoek van 45 graden moeten tekenen, zien we dat de lichtstralen nu op onverwachte plekken reflecteren. In het linker voorbeeld hadden we al geconcludeerd dat deze punten op de x'-as lagen. Vanaf de aarde gezien staat de x'-as dus ook onder een hoek (zie de rechter afbeelding). In de onderstaande afbeelding zien we het uiteindelijke ruimtetijd-diagram. We noemen dit ook wel een Minkowski-diagram. Merk op dat de hoek tussen de ct- en de ct'-as even groot is als de hoek tussen de x- en de x'-as. Ook zijn de stapjes op de x' en de ct' even groot.
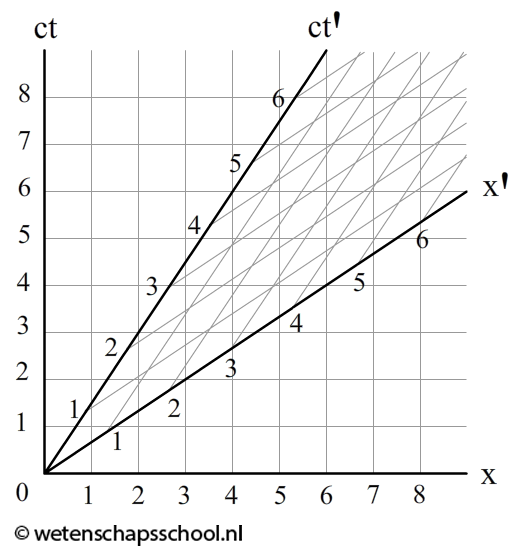
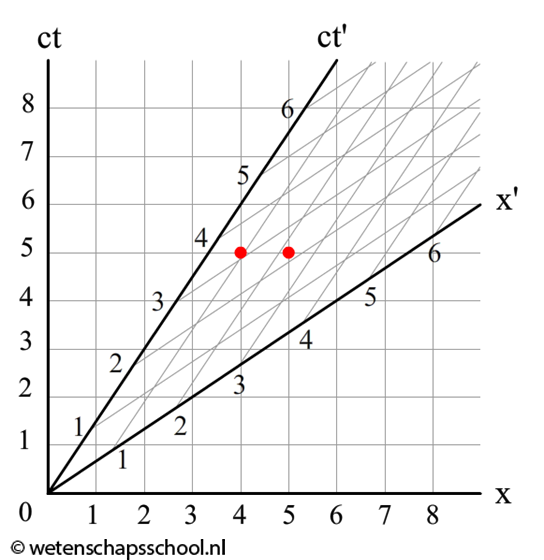
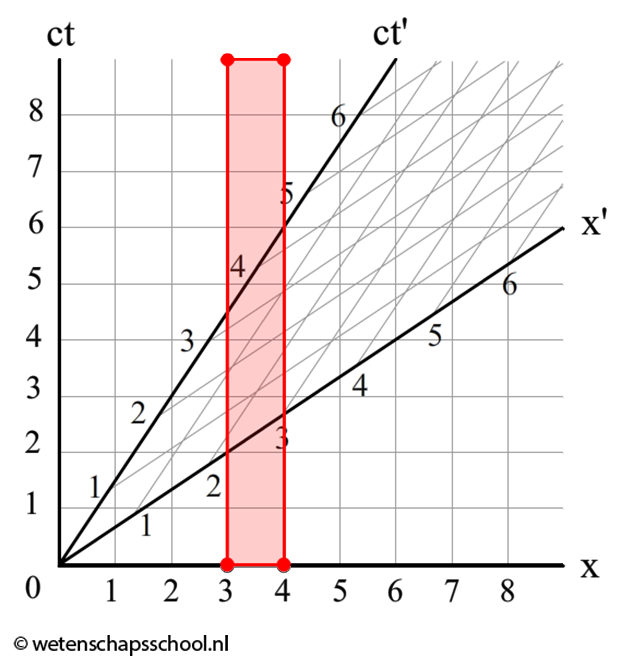
Laten we nu oefenen moet het aflezen van Minkowski-diagrammen. In de onderstaande linker afbeelding zien we een zevental gebeurtenissen die zijn aangegeven met rode punten. Volgens de persoon op aarde (x,ct) vinden deze gebeurtenissen na elkaar plaats. Het meest linkse punt gebeurt het eerst en het meest rechtse punt het laatst. In het bewegende systeem gebeuren al deze gebeurtenissen echter tegelijk! Al deze gebeurtenissen gebeuren namelijk op tijdstip ct' = 0. Dit is wederom de relativiteit van gelijktijdigheid.
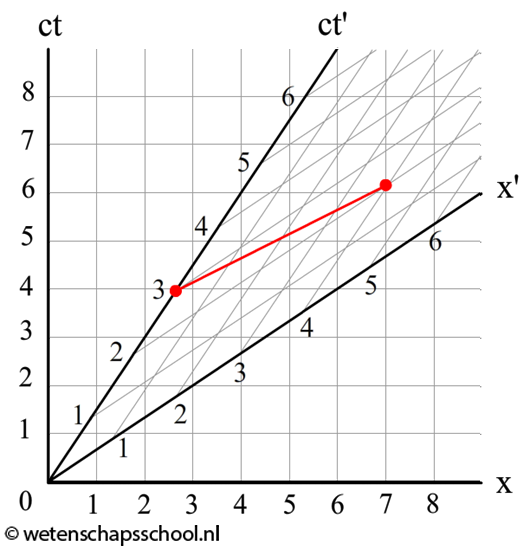
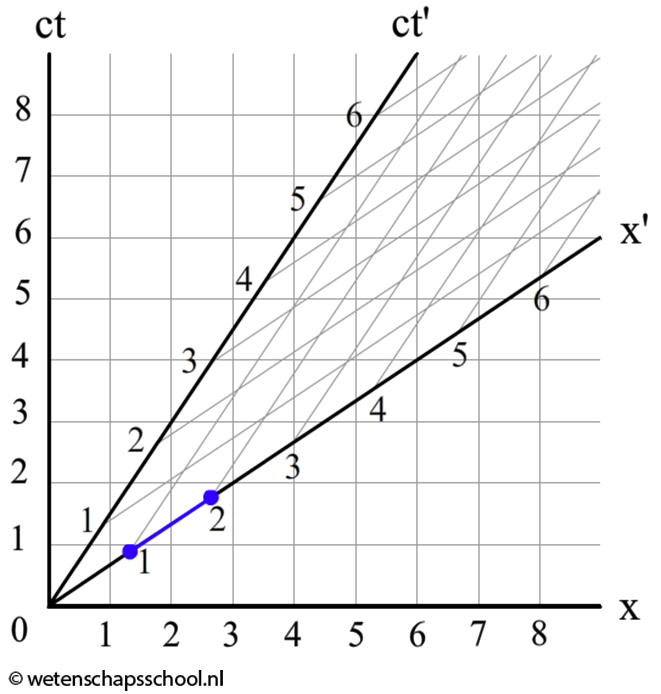
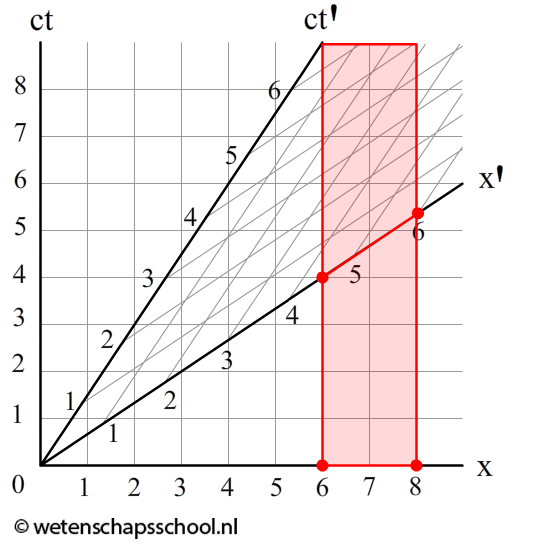
Ook lengtecontractie kunnen we uit het Minkowski-diagram aflezen. In het rechter diagram beschrijven we een voorwerp van 2,0 m dat stil ligt op aarde. Als we de lengte meten in het (x,ct)-stelsel, dan zien we dat de stok inderdaad 2,0 m is. In het bewegende stelsel is de afstand echter gelijk aan 1,5 m! Precies wat we volgens de formule van de lengtecontractie zouden verwachten:
$$L = \frac{L_{eigen}}{\gamma}$$ $$L = \frac{2}{1,34} = 1,5 \text{ m}$$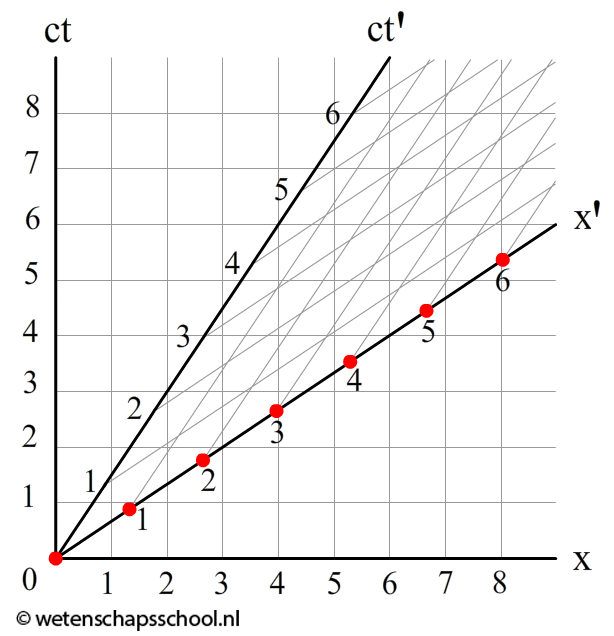
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|