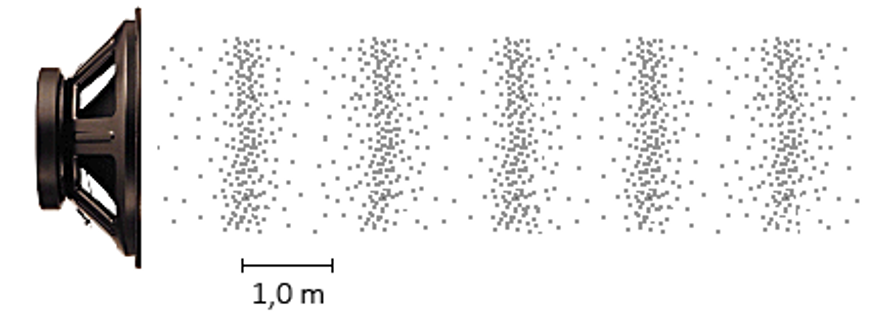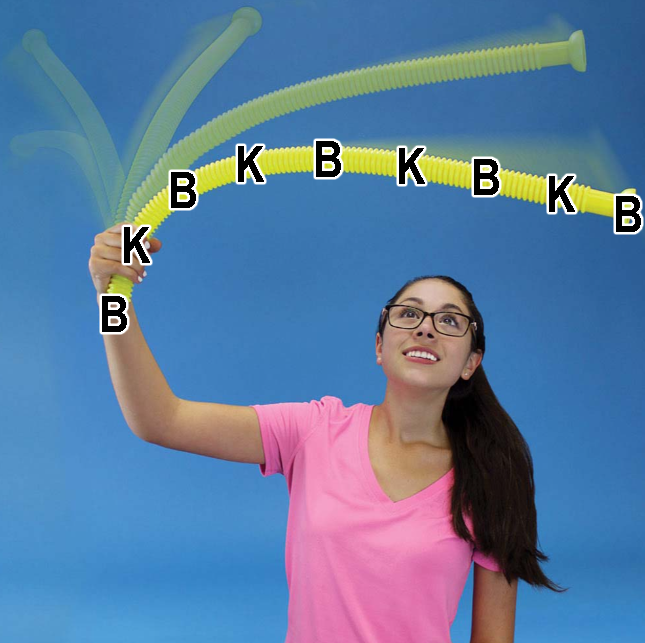ENERGIE

TRILLINGEN

RADIOACTIVITEIT

OPTICA (HAVO)

antwoorden

antwoorden

antwoorden

antwoorden

videolessen

videolessen

videolessen

videolessen

oefentoets

oefentoets

oefentoets

oefentoets

RELATIVITEIT (VWO)

DEELTJESFYSICA (VWO)

...

...

antwoorden

antwoorden

antwoorden

antwoorden

videolessen

videolessen

videolessen

videolessen

Hoofdstuk 2
Trillingen

§1 Trillingen
§2 De harmonische trilling
§3 Resonantie
§4 Golven
§5 Faseverschil (VWO)
§6 Interferentie (VWO)
§7 Staande golven

§1     Trillingen

In dit hoofdstuk gaan we trillingen en golven bestuderen. Hiermee kunnen we o.a. de werking van muziekinstrumenten begrijpen. In deze paragraaf gaan we rekenen met de trillingstijd en de frequentie.

Een trilling is het simpel heen en weer bewegen van een voorwerp. Een simpel voorbeeld van een trilling wordt uitgevoerd door het zogenaamde massa-veersysteem. Dit systeem bestaat uit een blokje dat met behulp van een veer heen en weer beweegt over een wrijvingsloos horizontaal oppervlak (zie de onderstaande animatie)(zie de onderstaande afbeelding).

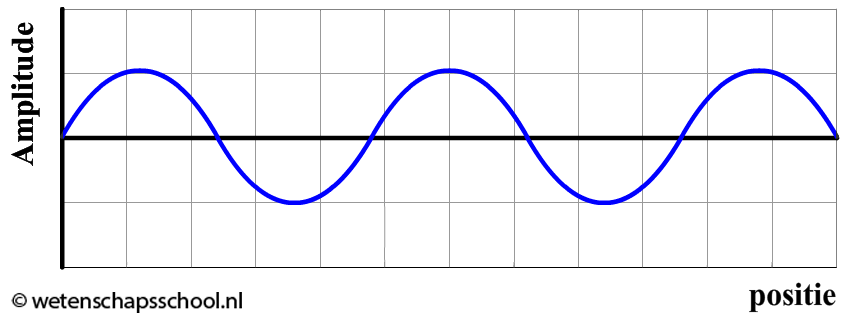
Zoals je kunt zien, beweegt het blokje heen en weer om het punt u = 0 m. We noemen deze positie de evenwichtsstand. Als het blokje zich hier bevindt, dan bevindt de veer zich in zijn neutrale positie. Rechts van dit punt is de veer uitgerekt. Links van dit punt is de veer ingedrukt. De afstand van het midden van het blokje tot deze evenwichtstand noemen we de uitwijking (u). De maximale uitwijking van het blokje tijdens de trilling noemen we de amplitude (A).

Ook geluid wordt veroorzaakt door trillingen. In dit geval gaat het om het trillen van luchtdeeltjes. We kunnen deze trillingen zichtbaar maken met een oscilloscoop (zie de onderstaande afbeelding). Het oscilloscoopbeeld kan worden opgevat als een diagram met op de horizontale as de tijd (t) en op de verticale as de uitwijking (u). We spreken hier daarom ook wel van een (u,t)-diagram.

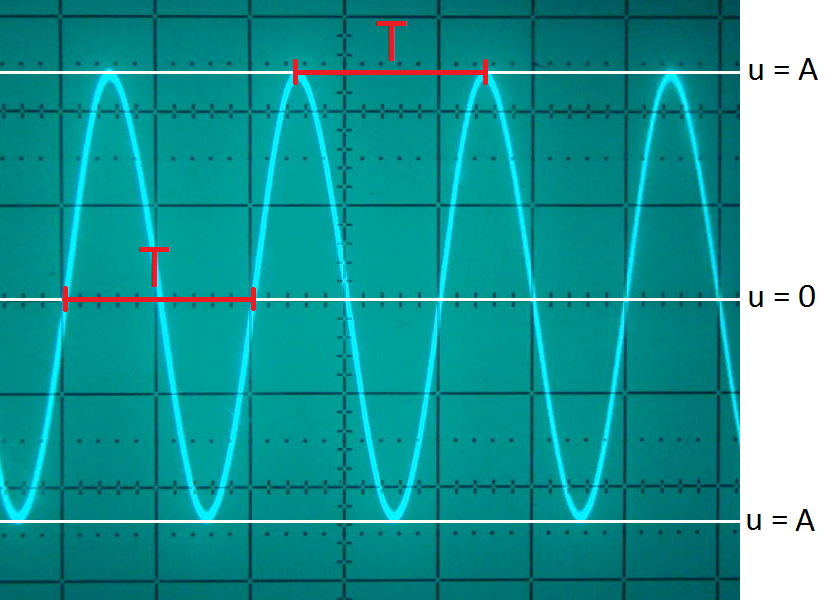
De bovenstaande trilling herhaalt zich in de tijd. We noemen een dergelijke beweging een periodieke beweging. De trillingstijd (T) (ook wel de periode genoemd) geeft aan hoe lang het duurt voordat de beweging zich herhaalt. In de bovenstaande afbeelding zien we twee manieren om de trillingstijd te meten.

De grootte van elk hokje op de horizontale as van het oscilloscoopbeeld wordt gemeten in ms/div. "div" staat hier voor "division", hetgeen we in het Nederlands "hokje" zouden noemen. Een waarde van 10 ms/div betekent bijvoorbeeld dat elk hokje op de horizontale as overeenkomt met 10 milliseconden.

Met de trillingstijd kunnen we o.a. de frequentie (f) bepalen. We meten de frequentie in hertz (Hz) en dit komt overeen met het aantal trillingen per seconde. Er geldt:

$$f = \frac{1}{T} $$ Trillingstijd (T) seconde (s) Frequentie (f) hertz (Hz)

Let erop dat je de trillingstijd in deze formule altijd in seconden invult.

Laten we eens het oscilloscoopbeeld van een aantal tonen vergelijken. Hieronder zien we aan de linkerzijde een oscilloscoopbeeld van een zachte en een harde toon. Zoals je kunt zien heeft een zachte toon een kleine amplitude en heeft de harde toon een grote amplitude. De "hardheid" van het geluid noemen we in de natuurkunde de geluidsterkte. We meten de geluidsterkte in decibel (dB). Aan de rechterkant zien we een oscilloscoopbeeld van een lage en een hoge toon. Zoals je kunt zien heeft een lage toon een lage frequentie (en een grote trillingstijd) en heeft een hoge toon een hoge frequentie (en een lage trillingstijd). De frequentie van een toon bepaald dus de toonhoogte van het geluid.

Voorbeeld

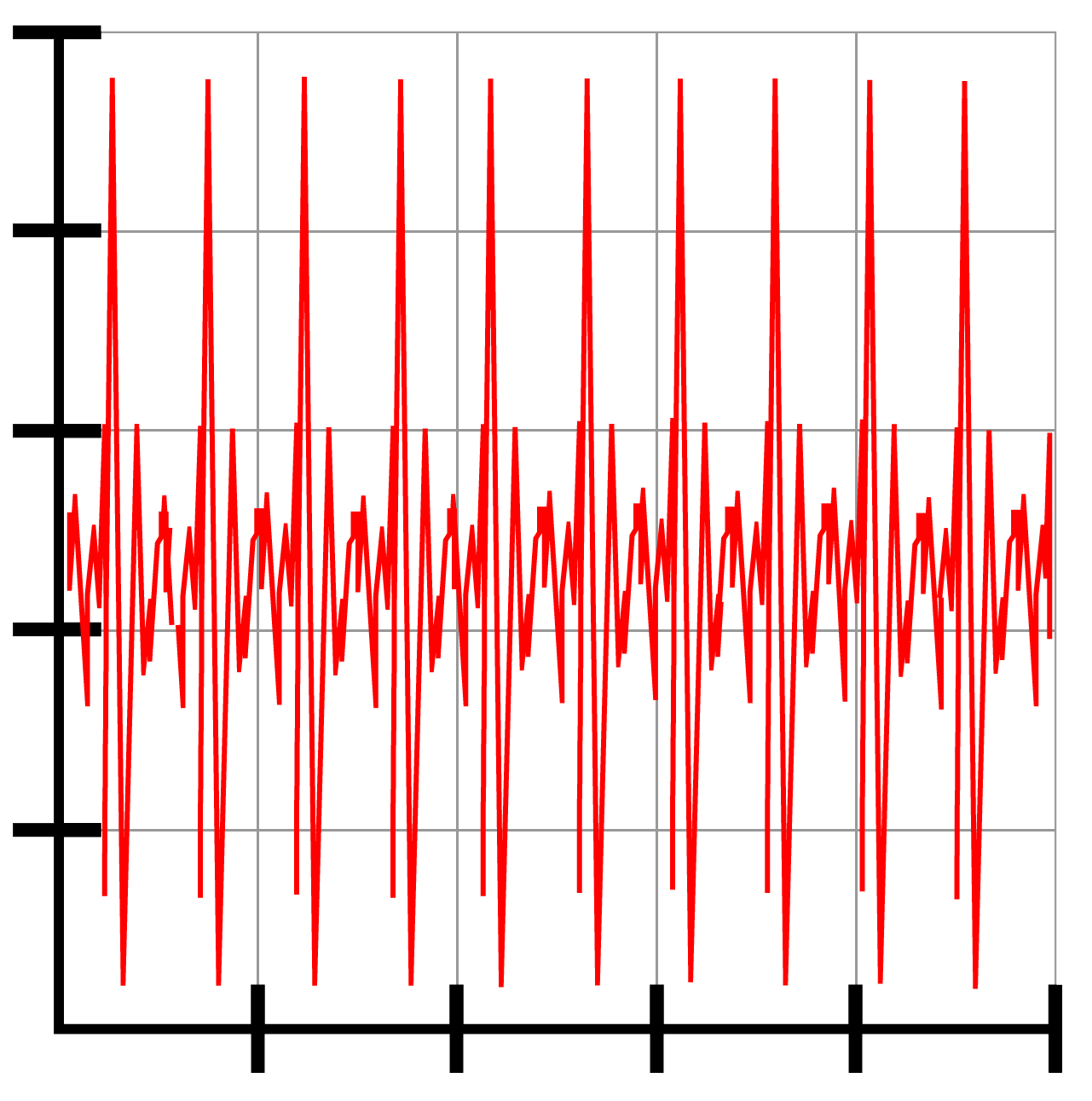
Vraag: Bepaal de frequentie van het onderstaande oscilloscoopbeeld van een saxofoon. De oscilloscoop is ingesteld op 5 ms/div. Antwoord: De tijdsduur behorende bij één trilling is in dit geval lastig nauwkeurig af te lezen. Het is hier daarom noodzakelijk om de trillingstijd van zoveel mogelijk trillingen tezamen te meten. Als we netjes meten, dan vinden we bijvoorbeeld dat 10 trillingen overeenkomen met 4,75 hokjes (ga dit zelf na). Eén trilling komt dan overeen met: $$ \frac{4,75}{10} = 0,475 \text{ hokjes} $$ Omdat de oscilloscoop is ingesteld op 5 milliseconde per hokje, vinden we: $$ 0,475 \times 5 = 2,375 \text{ ms} $$ In seconden wordt dit: $$ T = \frac{2,375}{1000} = 0,002375 \text{ s} $$ Met de formule voor de frequentie vinden we dan: $$ f = \frac{1}{T} \;\;\;\;\;\;\;\; f = \frac{1}{0,002375} = 421 \text{ Hz} $$

Bij muziekinstrumenten wordt de toonhoogte meestal niet gegeven in hertz, maar gebruiken we letters. De toon a1 komt bijvoorbeeld overeen met een frequentie van 440 Hz. In BINAS kan je vinden welke tonen overeenkomen met welke frequenties.

Leerdoelen:

Zorg dat je een trilling kan beschrijven met behulp van de uitwijking, de amplitude en de trillingstijd. Zorg dat je de trillingstijd kan bepalen met het (u,t)-diagram op een oscilloscoopbeeld en de bijbehorende stapgrootte in ms/div. Lees voor een nauwkeurig antwoord de tijd van zo veel mogelijk trillingen af. Deel deze tijd daarna door het aantal trillingen. Zorg dat je kan rekenen met "f = 1/T" en zorg dat je weet dat een grotere trillingstijd zorgt voor een kleinere frequentie en andersom. Zorg dat je weet dat een hardere toon (een grotere geluidsterkte) op een oscilloscoop een grotere amplitude heeft en dat een hogere toon een grotere frequentie (en dus een kleinere trillingstijd) heeft.

Opdrachten

(3p) Een luidspreker produceert een toon van 2035 Hz. Bereken de trillingstijd van deze toon in milliseconden. (3p) Een boom waait 5x heen en weer in 10 seconden. Bereken de trillingstijd en de frequentie. Een kolibrie beweegt tijdens het vliegen zijn vleugels erg snel op en neer. Hierdoor is een zoemend geluid te horen met een frequentie van 55 Hz. (2p) Bereken hoelang één trilling van de vleugels duurt. (3p) De beweging wordt vastgelegd met een camera die 1100 beelden per seconde kan maken. Bereken hoeveel frames nodig zijn om één trilling van de vleugel van de kolibrie vast te leggen. (1p) Een saxofonist speelt twee tonen. De tweede toon heeft een grotere frequentie. Leg uit of de trillingstijd groter of kleiner is geworden? (2p) Gezoem van een mug heeft een hogere toonhoogte dan het gezoem van bijvoorbeeld een hommel. Welk insect beweegt zijn vleugels vaker op en neer in een bepaalde tijd? Een pianotoets wordt eerst hard en dan zacht aangeslagen. (1p) Leg uit of de frequentie verschilt. (1p) Leg uit of de trillingstijd verschilt. (1p) Leg uit of de amplitude verschilt. (4p) Een saxofonist speelt twee tonen. De eerste toon is laag en heel hard. De tweede toon is juist hoog en zacht. Teken hoe de twee tonen eruit zien op de oscilloscoop. Een stemvork wordt aangeslagen. Na verloop van tijd wordt de toon steeds zachter hoorbaar. (1p) Leg uit of de frequentie verandert tijdens het zachter worden van het geluid. (1p) Leg uit of de amplitude verandert tijdens het zachter worden van het geluid. (4p) Teken het (u,t)-diagram van een trillend voorwerp met een frequentie van 3,5 Hz en een amplitude van 2,5 cm. (2p) Bij het aflezen van een oscilloscoopbeeld is het gebruikelijk om de tijdsduur van meerdere trillingen tegelijk op te meten. Vertel waarom dit zo is. Hieronder zien we het oscilloscoopbeeld van een zuivere toon. De tijdsbasis is 5,0 ms/div. 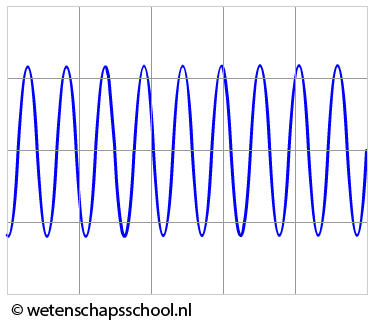(5p) Bereken de frequentie van deze toon. (1p) Dezelfde toon een octaaf lager heeft een twee keer zo kleine frequentie. Teken het oscilloscoopbeeld van deze toon met dezelfde tijdsbasis. Hieronder zien we het oscilloscoopbeeld van een zuivere toon. De tijdsbasis is 0,20 ms/div. 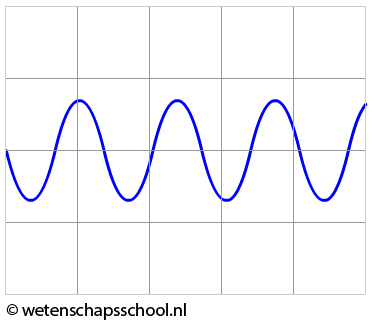(4p) Bereken de frequentie van deze toon. (1p) Teken dezelfde toon als we de tijdsbasis op 0,40 ms/div zouden zetten. 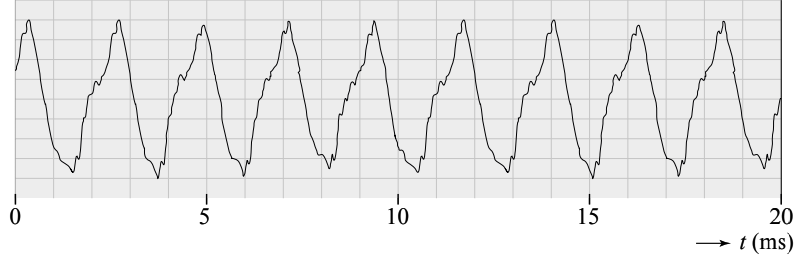(4p) Bepaal met behulp van BINAS de toon die hieronder is weergegeven: (bron: examen VWO 2009-1) (3p) Een elektrocardiogram (ECG), ook wel een "hartfilmpje" genoemd, meet de spanning waarmee de hartspier bloed rondpompt. Hieronder zien we een ECG die is ingesteld op 0,20 s/div. Bepaal de hartslag in "beats per minute" (bpm).

 

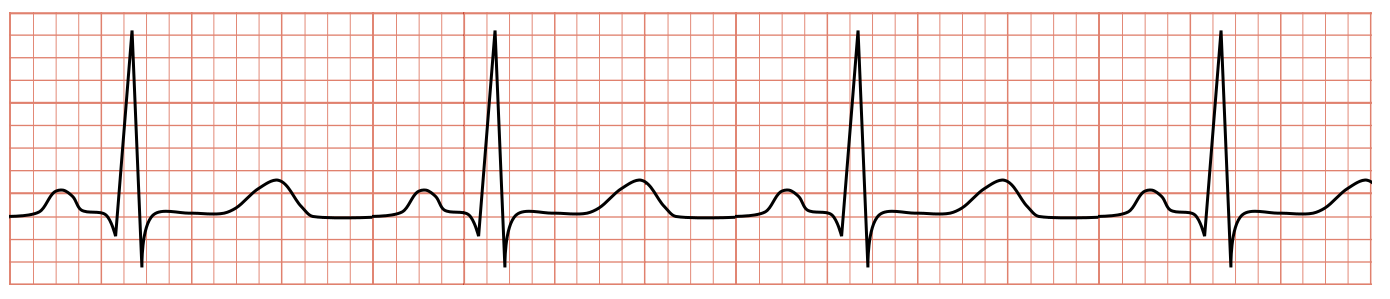
§2     De harmonische trilling

In deze paragraaf gaan we de zogenaamde harmonische trilling bestuderen.

De trilling die een massa-veersysteem uitvoert, noemen we een harmonische trilling. Deze trilling ziet er in een (u,t)-diagram als volgt uit:

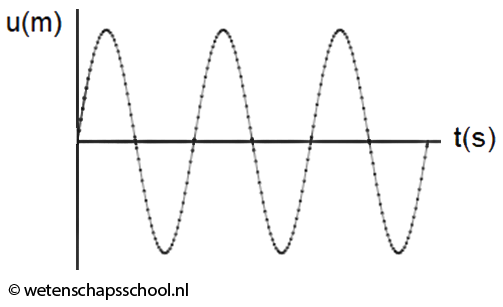
Met behulp van de tweede wet van Newton is af te leiden dat voor elke harmonische trilling geldt dat:

$$T = 2\pi \sqrt{\frac{m}{C}}$$ Trillingstijd (T) seconde (s) Massa (m) kilogram (kg) Veerconstante (C) newton per meter (N/m)

VWO

Voor elke harmonische trilling geldt ook dat: $$F_{res} = -Cu$$ Resulterende kracht (Fres) newton (N) Constante (C) newton per meter (N/m) Uitwijking (u) meter (m)   Bij het massa-veersysteem is de resulterende kracht in deze formule gelijk aan de veerkracht. De "min" in de formule zorgt ervoor dat de kracht automatisch in de juiste richting wijst. Dit is goed de zien in de onderstaande animatie.Dit is goed te zien in de animatie op de website. Als het blokje zich links van de evenwichtstand bevindt (u < 0), dan werkt de veerkracht naar rechts (F > 0). Als het blokje zich rechts van de evenwichtstand bevindt (u > 0), dan werkt de veerkracht naar links (F < 0). Als we met deze formule een model maken, dan vinden we de volgende trilling: AFBEELDING De volgende formule hoort bij de grafiek die bij dit model ontstaat: $$u = A \sin{\left(2\pi \frac{t}{T}\right)} \;\;\;\; \textbf{(radialen)}$$ Uitwijking (u) meter (m) Amplitude (A) meter (m) Tijd (t) seconde (s) Trillingstijd (T) seconde (s)   Let erop dat je bij gebruik van deze formule de rekenmachine op radialen zet. Als laatste kijken we naar de energieomzetting bij een harmonische trilling. Tijdens de beweging zet het blokje telkens veerenergie (1/2Cu2) en kinetische energie (1/2mv2) in elkaar om. Aan de uiteinden van de beweging is de snelheid nul. De kinetische energie is hier dus ook nul. Er is hier echter wel een veerenergie. Omdat de uitwijking hier gelijk is aan de amplitude, vinden we dat de totale energie aan de uiteinden gelijk is aan: $$E_{tot} = \frac{1}{2}CA^2 \;\;\;\;\;\;\; \text{(uiteinden)}$$ In de evenwichtstand is de uitwijking nul. Er is hier dus geen veerenergie. De snelheid is hier maximaal en als gevolg hebben we hier wel een kinetische energie. In de evenwichtsstand is de totale energie dus gelijk aan: $$E_{tot} = \frac{1}{2}mv_{max}^2 \;\;\;\;\;\;\; \text{(evenwicht)}$$ In een filmpje op we website laten we zien dat je hiermee de volgende formule kan afleiden:  $$ v_{max} = \frac{2\pi A}{T}$$ Maximale snelheid (vmax)  meter per seconde (m/s) Amplitude (A) meter (m) Trillingstijd (T) seconde (s)

Leerdoelen:

Zorg dat je weet dat o.a. een trillend blokje aan een veer zonder wrijvingskracht een harmonische trilling uitvoert. Voor een harmonische trilling geldt "T = 2π√(m/C)". Zorg dat je deze formule kan omschrijven. (VWO) Zorg dat je weet dat voor een harmonische trilling ook geldt dat "Fres = -Cu". De "min" zorgt ervoor dat de kracht altijd richting de evenwichtsstand werkt. (VWO) Ook geldt voor harmonische trillingen dat "u = Asin(2πt/T)", waarbij de rekenmachine op radialen ingesteld moet worden. Ook geldt bij de harmonische trilling de formule "vmax = 2πA/T".

Opdrachten

Een ouder heeft een wieg gekocht. De wieg hangt aan een veer en kan zachtjes op en neer trillen. De veerconstante is 1,3 kN/m en de massa van de wieg is 12,2 kg. (3p) Bereken hoe ver de veer is uitgerekt als de wieg stil aan de veer hangt. (4p) De ouder legt haar baby van 3,2 kg in de wieg. Door de wieg een beetje uit zijn evenwichtsstand te duwen, begint de wieg een trilling uit te voeren. Bereken de frequentie van deze trilling. (2p) De ouder heeft gelezen dat baby's gemakkelijker in slaap vallen als de frequentie van het trillen kleiner is. Noem twee aanpassingen aan de wieg waarmee de frequentie van de wieg kleiner kan worden gemaakt. Licht je antwoord toe. (bron: examen HAVO 2016-2) (3p) In de onderstaande afbeelding is een speeldoosje weergegeven. Via een hendel en een tandwielconstructie kan een rol in beweging worden gebracht. Op deze rol zijn puntjes aangebracht, waarmee de uiteinden van metalen strips worden opgetild en daarna losgelaten. Leg uit of de toonhoogte van de melodie lager wordt, gelijk blijft of hoger wordt, als de hendel sneller wordt rondgedraaid. (bron: examen VWO 2017-2) In het molecuul waterstofjodide (HI) is een waterstofatoom gebonden aan een veel zwaarder jodiumatoom. De evenwichtsafstand tussen de twee atomen is 1,609 × 10-10 m. Als deze afstand groter of kleiner wordt, zorgt de binding voor een terugdrijvende kracht die in eerste benadering zorgt voor een harmonische trilling. (5p) De trillingsfrequentie van dit massa-veersysteem is 6,92 × 1013 Hz. Bereken hiermee de veerconstante van deze trilling. (VWO, 3p) Bij een bepaalde temperatuur bedraagt de trillingsenergie van het waterstofatoom 6,0 × 10-20 J. Bereken hiermee de maximum snelheid van het waterstofatoom. (VWO, 3p) Bereken de maximale afstand tussen de atomen tijdens het trillen. (VWO, 1p) Het waterstofatoom bevindt zich langere tijd rond de maximale uitwijkingen van de beweging dan rond de evenwichtsstand. Leg uit hoe dit komt.

 

§3     Resonantie

In sommige omstandigheden neemt de amplitude van een trilling extreem sterk toe. We spreken in deze gevallen van resonantie. In deze paragraaf gaan we begrijpen hoe resonantie werkt.

In de vorige paragraaf zagen we dat voor een harmonische trilling geldt dat:

$$T = 2\pi \sqrt{\frac{m}{C}}$$

We zien hier dat deze harmonische trilling alleen afhankelijk is van twee constanten: de massa en de veerconstante. Elk harmonisch trillend systeem heeft dus zijn eigen vaste trillingstijd (T_eigen). Omdat geldt dat f = 1/T, heeft elk harmonisch trillend systeem ook een eigen vaste frequentie. We noemen dit de eigenfrequentie (f_eigen).

Bij een harmonische trilling wordt een voorwerp uit zijn evenwichtsstand gehaald, maar daarna laat men het voorwerp vrij heen en weer bewegen. We noemen dit ook wel een ongedwongen trilling. We kunnen een trilling ook continu aandrijven. We spreken in dat geval van een gedwongen trilling. Denk bijvoorbeeld aan een schommel die we elke keer weer een duw blijven geven.

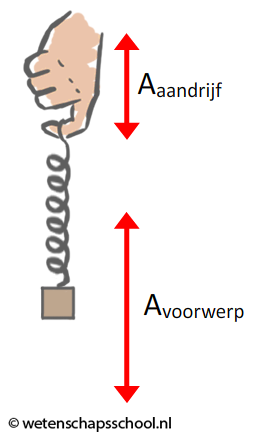
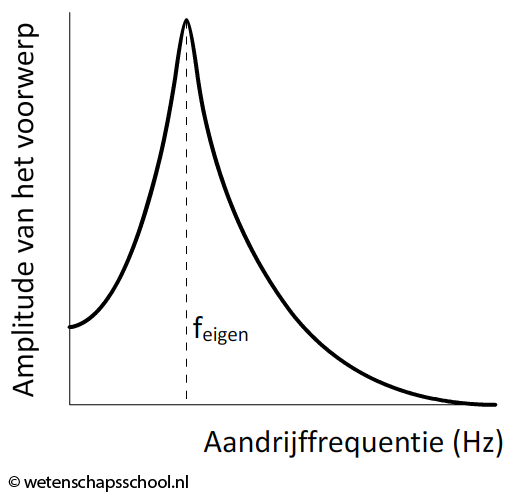
Hierboven zien we aan de linkerzijde nog een voorbeeld van een gedwongen trilling. Een blokje wordt hier aangedreven door het op en neer bewegen van een hand. Bij de meeste aandrijffrequenties zal het blokje niet erg reageren op de beweging van de hand. Er is echter één aandrijffrequentie waarbij de amplitude van het blokje gigantisch toeneemt (zie de bovenstaande grafiek). De amplitude van de beweging van het blokje kan hier zelfs vele malen groter worden dan de amplitude van de hand. Deze bijzondere aandrijffrequentie blijkt precies gelijk te zijn aan de eigenfrequentie van het systeem. We noemen dit effect resonantie:

• Resonantie is de dramatische toename van de amplitude van een systeem door dit systeem aan te drijven met zijn eigenfrequentie.

Een bekend voorbeeld van resonantie is de schommel. We weten allemaal uit ervaring dat we de schommel het beste een zetje kunnen geven als de schommel zich op zijn achterste punt bevindt. Als we telkens op dit moment duwen, dan duwen we precies met de eigenfrequentie van de schommel. Duw je te laat of te vroeg, dan is het effect minder of rem je de schommel juist af.

Nog een voorbeeld. Als we een stemvork aanslaan, dan is een zacht geluid te horen. Als we deze stemvork echter op een speciaal ontworpen klankkast plaatsen, dan horen we een hard geluid. De klankkast is namelijk zo ontworpen dat de eigenfrequentie van de lucht in de klankkast gelijk is aan de eigenfrequentie van de stemvork. De luchtdeeltjes in de klankkast gaan daarom resoneren en dit zorgt ervoor dat we het geluid beter kunnen horen. Hetzelfde effect zien we bij de klankkast van een gitaar.

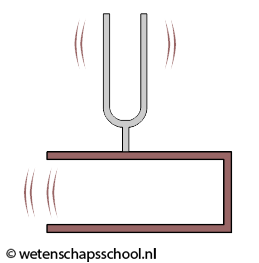
Hieronder zien we twee dezelfde stemvorken die tegenover elkaar staan. Als je de ene stemvork aanslaat, dan gaat de andere automatisch meetrillen omdat de eigenfrequenties van beide stemvorken gelijk zijn. Ook dit is dus resonantie. Doen we hetzelfde experiment met twee verschillende stemvorken, dan werkt dit niet. De tweede stemvork trilt nu niet mee.

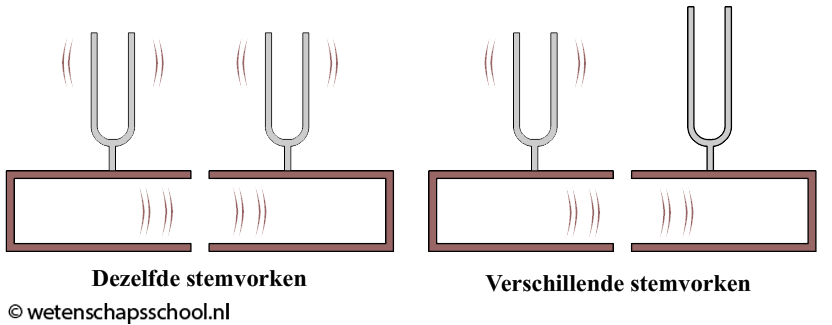
Demonstratievideo

In het rechter filmpje wordt dit fenomeen gedemonsteerd: DEMO-VIDEO: Resonantie stemvorken

Demonstratievideo

In het rechter filmpje zien we drie blokken met verschillende massa's en dus ook verschillende eigenfrequenties. Met een toongenerator zoeken we deze eigenfrequenties op, waardoor de blokken gaan resoneren: DEMO-VIDEO: Resonantie veren

Demonstratievideo

In het rechter filmpje wordt met geluid de eigenfrequentie van een wijnglas gevonden. Hierdoor breekt het glas. Bij een hogere of een lagere frequentie vindt geen resonantie plaats en blijft het glas heel. DEMO-VIDEO: Resonantie wijnglas

Demonstratievideo

Hiernaast zien we een filmpje van een brug die in 1940 instortte doordat de wind een periodieke kracht uitoefende met een frequentie die precies gelijk was aan de eigenfrequentie van de brug. DEMO-VIDEO: Resonantie brug

Demonstratievideo

Hiernaast zien we resonantie optreden bij een aantal slingers. De eigenfrequentie van een slinger hangt af van de lengte. Een van de slingers wordt in beweging gebracht en alleen de slinger met dezelfde lengte gaat hierdoor resoneren: DEMO-VIDEO: Resonantie slingers

Leerdoelen:

Zorg dat je weet dat voorwerpen een eigenfrequentie (of eigenfrequenties) hebben. Dit is de frequentie waarbij het voorwerp ongedwongen trilt. Zorg dat je weet dat als je een voorwerp gedrongen in trilling brengt in zijn eigenfrequentie, dat dan resonantie optreedt. Dit is de dramatische toename van de amplitude van het voorwerp. Bij andere frequenties is de amplitude klein. Zorg dat je begrijpt dat o.a. de lengte van een klankkast van een stemvork zo gekozen is dat de lucht in de klankkast resoneert met de stemvork en zo het geluid versterkt.

Opdrachten

(1p) Leg uit wat resonantie is. (2p) Als je een stemvork goed wilt horen, dan wordt deze bevestigd op een klankkast met een specifieke lengte. Leg uit waarom de lengte van de klankkast van belang is. In de onderstaande afbeelding zien we links twee dezelfde stemvorken. Als je de ene stemvork aanslaat, dan gaat de ander meetrillen. (1p) Leg uit waarom dit gebeurt. (1p) In de rechter afbeelding zijn de stemvorken niet gelijk. Leg uit waarom in dit geval de stemvork niet gaat meetrillen. (1p) Als je over de opening van een fles blaast, dan hoor je een harde toon. Leg uit hoe dit komt. Gebruik hierbij het woord resonantie. Als je met een bepaalde snelheid over een hobbelige weg fietst, dan kan je fiets opeens behoorlijk gaan trillen. (1p) Leg uit of het helpt om langzamer te gaan rijden. (1p) Leg uit of het helpt om sneller te gaan rijden. (3p) Een persoon houdt de bovenkant van een veer vast en bevestigd aan de onderkant een blokje. Het blokje heeft een massa van 20 gram en de veerconstante van de veer is 50 N/m. Bereken met welke frequentie je de veer op en neer moet bewegen om resonantie te krijgen. Een auto met een eigenfrequentie van 1,3 Hz rijdt op een weg met hobbels. De hobbels zijn 12 m van elkaar verwijderd. (3p) Bereken de snelheid die de auto moet hebben om de vering in de auto in resonantie te laten komen. (2p) De auto heeft een massa van 1,0 × 103 kg. Bereken de veerconstante van de vering van de auto. (3p) Stel dat we de massa van de auto groter maken, treedt deze resonantie dan op bij een grotere of een kleinere snelheid. Licht je antwoord toe. Een chauffeur van een vrachtwagen kan last krijgen van trillingen die veroorzaakt worden door de motor van de vrachtwagen. Deze trillingen worden via de chauffeursstoel aan de chauffeur doorgegeven. Deze trillingen kunnen, naast ongemak, ook schade aan de rug veroorzaken. In een bepaalde vrachtauto trilt de stoel met een frequentie van 2,8 Hz. Om dit op te lossen wordt de stoel op een veersysteem geplaatst. Hieronder zien we hoe de amplitude van de stoel met dit veersysteem ten opzichte van de amplitude van de vrachtwagen (vw) verandert als functie van de frequentie van de motor. 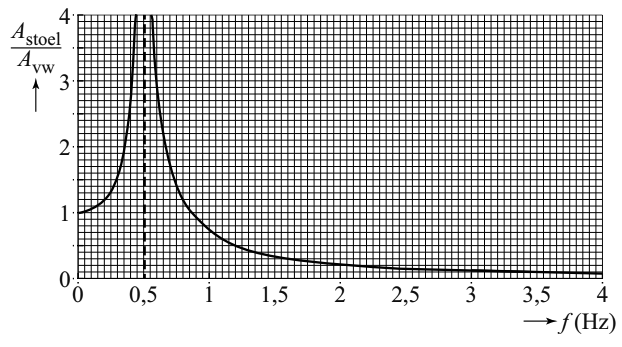(2p) Bij 0,5 Hz is in de grafiek een hoge piek te zien. Hoe is deze piek ontstaan en hoe wordt dit fenomeen genoemd? (3p) Leg uit bij welke frequenties dit veersysteem het trillen van de stoel vergroot en bij welke frequenties het trillen juist wordt verkleind. (1p) Leg uit dat het veersysteem ervoor zorgt dat de stoel minder gaat trillen. (4p) De chauffeur heeft een massa van 90 kg en de veerconstante van de veer in de stoel is C = 1,3 × 103 N/m. Bereken de massa van de stoel. (bron: examen HAVO 2016-1)

 

§4     Golven

In deze paragraaf beginnen we met het bestuderen van golven. We zullen leren de golfsnelheid te berekenen en we zullen leren golven weer te geven in zogenaamde (u,x)-diagrammen.

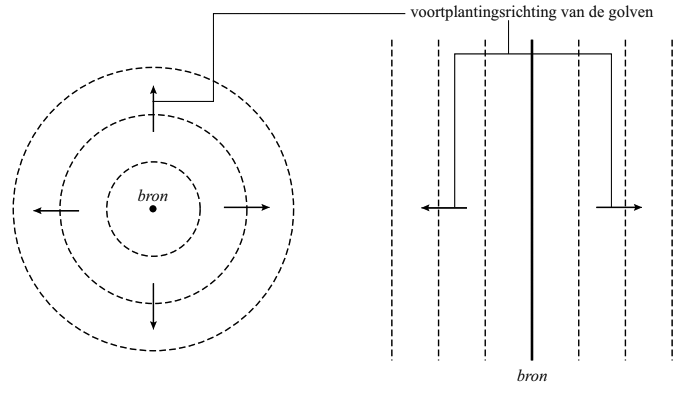
Hieronder is een animatie van een golf te zien. Hieronder zien we een afbeelding van een golf. Op de website kan je een animatie zien van het ontstaan van deze golf. Door het touw aan de linkerkant op en neer te bewegen, komt het hele touw in beweging. Elk stukje van het touw brengt het volgende stukje in beweging. We noemen de resulterende beweging een golf. Omdat de golf zich naar rechts verplaatst door het touw spreken we van een lopende golf.

Hoewel de golf zelf naar rechts beweegt, doen de deeltjes waaruit het touw bestaat dit niet. In de animatie kan je goed zien dat de deeltjes alleen op en neer bewegen. Elk deeltje voert dus een trilling uit die loodrecht staat op de beweging van de golf. Dit type golf wordt een transversale golf genoemd.

Ook in de lucht kunnen golven ontstaan. Dit worden geluidsgolven genoemd. Deze golven ontstaan als we een voorwerp in de lucht in trilling brengen. Dit gebeurt bijvoorbeeld bij het trillen van de conus van een speaker, het trillen van een gitaarsnaar of het trillen van stembanden.

In de onderstaande animatie zien we hoe geluidsgolven ontstaan. Op de website kan je ook een animatie van geluidsgolven zien. Het trillende voorwerp (links) botst tegen de omliggende luchtdeeltjes en deze luchtdeeltjes botsen weer tegen de volgende deeltjes etc. De beweging van de luchtdeeltjes zorgt ervoor dat er gebieden ontstaan met een hoge dichtheid (veel deeltjes) en met een lage dichtheid (weinig deeltjes). Deze gebieden van hoge en lage dichtheid vormen een golf die naar rechts beweegt. Het trommelvlies in ons oor kan in trilling worden gebracht door deze golf en zo nemen we geluid waar.

Als je de deeltjes in de animatie volgt, dan zie je dat alle deeltjes naar links en naar rechts bewegen om een evenwichtsstand. Elk deeltje voert dus een trilling uit. De beweging van al deze deeltjes samen zorgt voor een lopende golf die naar rechts beweegt. De deeltjes bewegen in dit geval evenwijdig aan de richting van de golf. We noemen dit longitudinale golven.

Geluidsgolven komen niet alleen in lucht voor. In elk materiaal kunnen geluidsgolven ontstaan. In metalen, bijvoorbeeld, kunnen geluidsgolven zelfs nog sneller voortplanten dan in de lucht. De stof waarin de geluidsgolven zich verplaatsen noemen we het medium. Als een ruimte geen medium bevat, dan spreken we van een vacuüm. In een vacuümruimte kan geluid niet voortplanten.

Demonstratievideo

In het rechter filmpje is te zien dat geluid inderdaad niet kan voortplanten in een vacuüm: DEMO-VIDEO: Geluid in vacuüm

De lengte van een golf noemen we de golflengte (λ). Hieronder is de golflengte aangegeven bij zowel een golf in een touw als een geluidsgolf. Bij geluidsgolven is de golflengte gelijk aan de afstand tussen twee opeenvolgende plekken met een maximale of een minimale dichtheid (zie de rechter afbeelding).

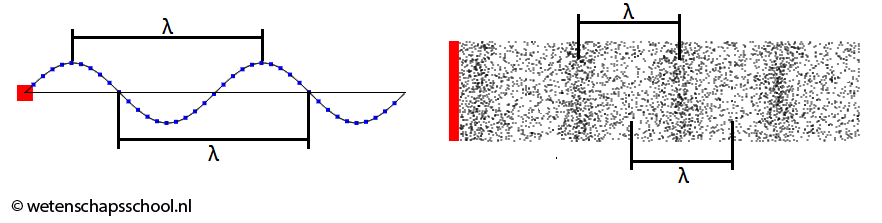
De snelheid van een golf meten we net als elke andere snelheid. Er geldt:

$$v_{golf} = \frac{\Delta x}{\Delta t}$$

We kunnen deze formule ook nog herschrijven in twee andere vormen. In de animatie van het ontstaan van een lopende golf aan het begin van de paragraaf zien we dat bij elke trilling van het linker blokje een extra golf in het touw ontstaat. Na elke trillingstijd is de golf dus een golflengte opgeschoven. We kunnen de formule voor de snelheid dus ook herschrijven tot:

$$v_{golf} = \frac{\lambda}{T}$$ Golfsnelheid (vgolf) meter per seconde (m/s) Golflengte (λ) meter (m) Trillingstijd (T) seconde (s)

Omdat f = 1/T, kunnen we deze formule ook schrijven als:

$$v_{golf} = \lambda f$$ Golfsnelheid (vgolf) meter per seconde (m/s) Golflengte (λ) meter (m) Frequentie (f) hertz (Hz)

In BINAS kan je voor een aantal stoffen de geluidsnelheid opzoeken. Deze geluidsnelheid is afhankelijk van de temperatuur. Let erop dat de temperaturen gegeven zijn in kelvin (K). Je kan als volgt graden Celsius omschrijven naar kelvin:

$$T(K) = T(^\circ C) + 273$$

T(K) staat voor de temperatuur in kelvin. T(^oC) staat voor de temperatuur in graden Celsius. Stel dat we lezen dat de temperatuur van lucht 20 ^oC is. Dit is gelijk aan 20 + 273 = 293 K. Volgens BINAS hoort bij deze temperatuur een geluidsnelheid van 0,343 × 10³ m/s. Dit is gelijk aan 343 m/s. Als in de vraag een temperatuur genoemd wordt, is dit dus vaak een aanwijzing dat de geluidsnelheid opgezocht moet worden.

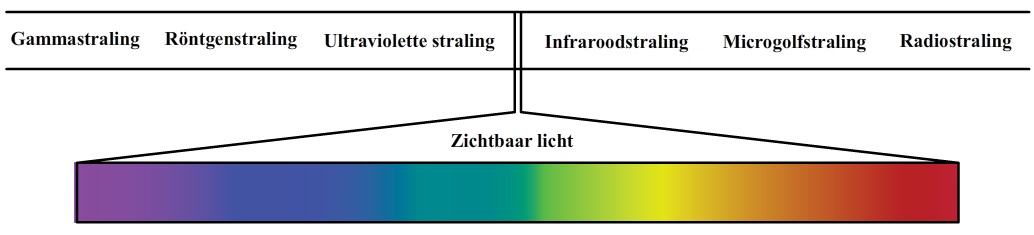
Ook licht bestaat uit golven en als gevolg zijn de bovenstaande formules voor de golfsnelheid ook voor licht van toepassing. Hieronder zien we het volledige spectrum van licht. Links van het paarse deel van het spectrum bevindt zich ultravioletstraling, röntgenstraling en gammastraling. Rechts van het rode deel van het spectrum hebben we infrarode straling, microgolfstraling en radiostraling. Zoals je in de onderstaande afbeelding kan zien is het zichtbare deel van het spectrum maar een klein deel van het gehele spectrum.

Al deze soorten licht (ook wel "straling" genoemd) bewegen met dezelfde snelheid "c". Er geldt:

$$v = c = 2,99792458 \times 10^8 \text{ m/s} $$

In een eerdere paragraaf hebben we gezien dat we trillingen beschrijven met een (u,t)-diagram. In het geval van golven gebruiken we het zogenaamde (u,x)-diagram. Een (u,x)-diagram is een "snapshot" van de golf op één bepaald moment. In de onderstaande twee (u,x)-diagrammen zien we bijvoorbeeld de beweging van een golfje door een touw op twee momenten afgebeeld. We zien dat het golfje in de tussentijd een stukje naar rechts opgeschoven is.

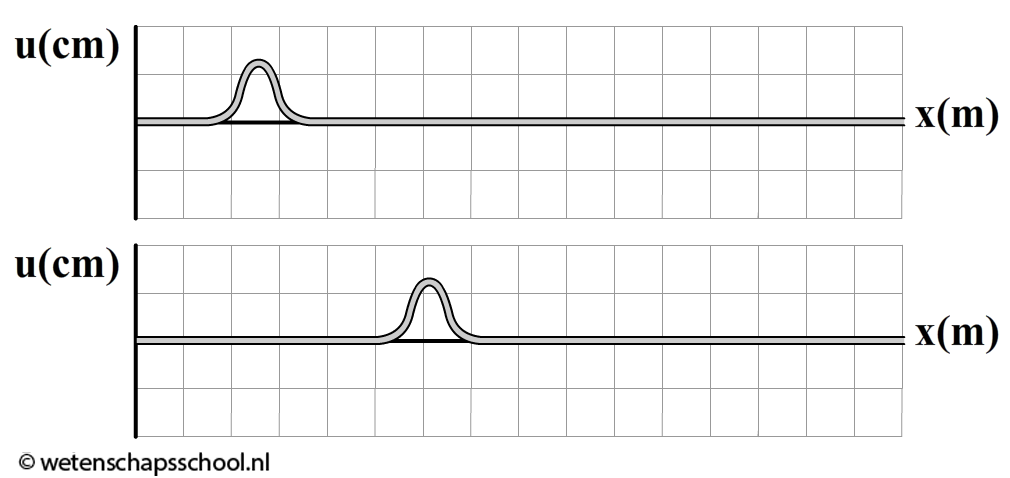
Met een (u,t)-diagram kunnen we de trillingstijd en de frequentie bepalen. Met een (u,x)-diagram kunnen we de golflengte bepalen.

In de onderstaande afbeelding zien we een golf ontstaan in een touw. Van elk punt van het touw kunnen we een (u,t)-diagram maken. In de rechter drie (u,t)-diagrammen is dit gedaan voor punt A, punt B en punt C. Zoals je links kunt zien beweegt punt A eerst omhoog, dan helemaal naar beneden en dan weer terug naar de evenwichtstand. Deze beweging is rechtsboven in het (u,t)-diagram weergegeven.

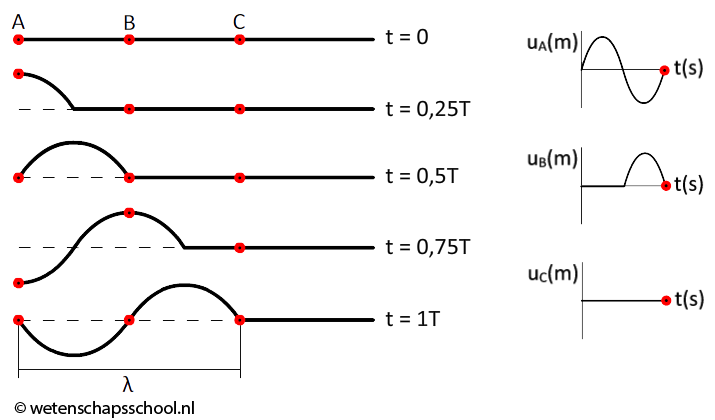
Van punt B is ook een (u,t)-diagram gemaakt. Het duurt eerst een halve trillingstijd voordat de golf punt B bereikt heeft. Gedurende deze tijd is de uitwijking dus nog nul. Dan beweegt punt B omhoog en weer naar beneden. Ook dit zien we terug in het (u,t)-diagram. Punt C wordt gedurende de hele beweging niet bereikt door de golf. De uitwijking is hier dus de gehele tijd gelijk aan nul.

Leerdoelen:

Zorg dat je het verschil tussen een trilling en een golf kan beschrijven. Zorg dat je weet dat bij een transversale golf de golfrichting loodrecht op de trillingsrichting staat en dat bij een longitudinale golf de golfrichting evenwijdig aan de trillingsrichting staat. Zorg dat je weet dat geluid een tussenstof of medium nodig heeft en dat in een vacuüm dus geen geluid mogelijk is Zorg dat je kan rekenen met de formule "vgolf = Δx/Δt" en "vgolf = λf" voor zowel geluid als licht, waarbij "λ" de golflengte is Zorg dat je de geluidsnelheid in verschillende stoffen in BINAS kan opzoeken aan de hand van de temperatuur in kelvin en zorg dat je de temperatuur van kelvin kan omrekenen naar graden Celsius en andersom. Zorg dat je de verschillende soorten elektromagnetische straling kent en in BINAS de bijbehorende golflengtes en frequenties kan opzoeken. Zorg dat je weet dat alle soorten elektromagnetische straling met de lichtsnelheid (c) voortplanten en zorg dat je hiermee kan rekenen met behulp van de formule "c = Δx/Δt". Houd er rekening mee dat geluid bij een echo twee keer dezelfde afstand aflegt Zorg dat je (u,x)- naar (u,t)-diagrammen kan omschrijven. Een (u,t)-diagram beschrijft de trilling van één punt in het (u,x)-diagram. Zorg dat je weet dat als een golf naar rechts beweegt, dat het meest rechtse deel van de golf als eerst geproduceerd is. In een (u,t)-diagram zal dit deel van de golf dus voor de eerste trilling zorgen.

Opdrachten

(2p) Leg uit wat het verschil is tussen een trilling en een golf. (1p) Waarom heeft geluid een medium nodig? (1p) Een bel wordt aangezet in een ruimte die langzaam vacuüm wordt gepompt. Leg uit wat er met het geluid gebeurt? (1p) Is een wave in een voetbalstadium een longitudinale of een transversale golf? (1p) Zoek de geluidsnelheid op in BINAS bij een temperatuur van 20 graden Celsius. (3p) Je ziet tijdens een hevige storm een bliksemflits. 8 seconden later hoor je de bijbehorende knal. Bereken hoe ver de bliksem van je vandaan was. De buitentemperatuur is 20 graden Celsius. (3p) Ook door gesteenten kunnen golven voortbewegen. De snelheid van deze golven is 5000 m/s. Het zijn deze golven die voor aardbevingen zorgen. Stel dat het epicentrum van een aardbeving 450 km van je vandaan ligt. Bereken hoelang het duurt voordat de aardbeving je bereikt. (4p) Met behulp van echo kan men bepalen hoe diep de zeebodem is. Men stuurt aan de onderkant van een schip een geluidspuls naar beneden en wacht hoelang het duurt voordat de puls tegen de bodem reflecteert en terug komt bij het schip. Stel dat de echo er 0,59 s over doet. Hoe diep is in dat geval de zeebodem. (4p) Bereken hoeveel minuten het duurt voordat zonlicht de aarde bereikt. (4p) Bij een ruimtereis naar de maan is een reflector geplaatst op het maanoppervlak. Door een laser vanaf de aarde naar deze reflector te schieten, kan de afstand tot de maan gemeten worden. Het laserlicht doet er 2560 ms over totdat het terug is op aarde. Bereken hiermee de afstand tot de maan. (1p) Draadloze telefonie en wifi werkt met behulp van radiosignalen. Wat is de snelheid van deze radiosignalen. 12. Sommige schepen hebben een radarinstallatie om de afstand tot andere schepen of voorwerpen in de omgeving te meten. Een radarinstallatie zendt hiervoor elektromagnetische signalen uit die weerkaatst worden door een voorwerp. Door de tijd tussen het uitzenden en het ontvangen van een signaal te meten, kan de afstand tot het voorwerp bepaald worden, ook als dat voorwerp zich op grote afstand van het schip bevindt. Een veelgebruikt type radar is de pulsradar. Dit type radar zendt een kort elektromagnetisch signaal uit en ontvangt even later de echo van dit signaal. Op een bepaald moment wordt er 0,26 ms gemeten tussen het uitzenden en het ontvangen van een signaal. (3p) Bereken de afstand tot het voorwerp. (3p) Het signaal is een puls die bestaat uit een aantal opeenvolgende elektromagnetische golven. Deze golven worden gemaakt met een vaste frequentie van 9,38 GHz. Eén puls duurt 0,100 μs. Bereken uit hoeveel golven één puls bestaat. (3p) Details met afmetingen van 10% van de golflengte zijn door de pulsradar net waar te nemen. Bereken de minimale afmeting van een voorwerp dat met deze pulsradar waar te nemen is. (bron: examen HAVO 2018-1) (3p) Aardbevingen worden gemeten met een seismograaf. Een seismograaf bestaat uit een dunne naald die door bevingen heen en weer gaat trillen over een stuk papier. Hieronder is zo’n trilling weergegeven. Zoals je ziet bestaat een beving uit drie delen. De zogenaamde P-golven zijn longitudinale golven en de S-golven zijn transversale golven. Omdat de longitudinale golven een iets grotere golfsnelheid hebben, komen ze iets eerder aan. Na de P- en S-golven volgen nog oppervlaktegolven. De horizontale as is ingesteld op 1,0 minuut/div. 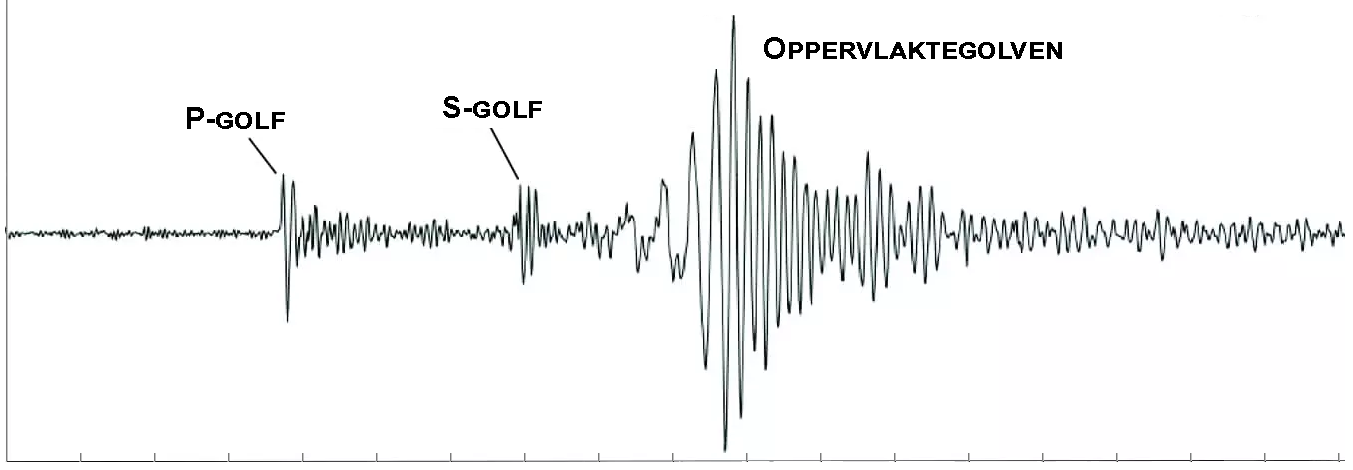Neem aan dat de longitudinale golven een snelheid hebben van vP = 4,9 km/s en de transversale golven een snelheid van vS = 3,4 km/s. Bereken met het tijdsverschil tussen de P- en S-golf op welke afstand het epicentrum van de aardbeving plaatsvond. Leid hiervoor eerst af dat: $$ \Delta t = \frac{\Delta x}{v_S} - \frac{\Delta x}{v_P} $$ Δt staat hier voor het tijdsverschil tussen de aankomst van de twee golven en Δx staat voor de afstand van de seismograaf tot het epicentrum van de aardbeving. (4p) Hieronder zie je een golf die is ontstaan in een touw. De persoon die de golf maakt beweegt het touw op en neer met een frequentie van 0,40 Hz. Bepaal de golfsnelheid van de golf in het touw zo nauwkeurig mogelijk. (5p) Hieronder zie je een geluidsgolf in een onbekend gas. De luidspreker produceert een toon van 150 Hz. Bepaal de geluidsnelheid in dit gas zo nauwkeurig mogelijk. 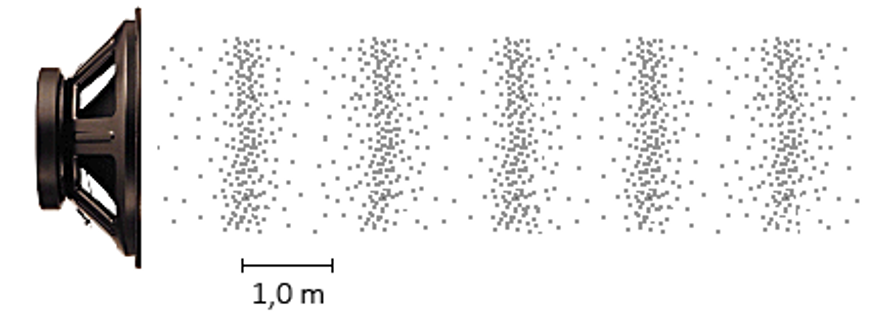(5p) In de onderstaande afbeelding zijn trillingen in een touw weergegeven. Deze trillingen zijn veroorzaakt doordat een persoon het touw aan de linker zijde in trilling heeft gebracht met een frequentie van 2,0 Hz. De horizontale as is ingesteld op 30 cm/div. Teken in de figuur de stand van het touw na 0,10 s. Schrijf ook de bijbehorende berekening op. De onderstaande afbeelding laat vereenvoudigd zien hoe een gedeelte van de zeebodem door een aardverschuiving plotseling omhoog komt. Hierdoor wordt zeewater omhoog geduwd waardoor er een "waterberg" aan het oppervlak ontstaat. Deze waterberg is meestal niet hoog, maar kan in de lengte en de breedte grote afmetingen hebben. Zo’n tsunami-golf verliest weinig aan hoogte als hij een grote afstand aflegt. Dit in tegenstelling tot een golf vanuit een puntvormige bron zoals bijvoorbeeld veroorzaakt door een steen die in een vijver valt. Hieronder worden beide situaties vergeleken. (2p) Leg uit waarom de amplitude van een golf in de linker afbeelding wel snel afneemt en in de rechter afbeelding (bijna) niet. (3p) In de onderstaande afbeelding zien we hoe de golf zich richting de kust verplaatst. De snelheid waarmee dit gebeurt, wordt gegeven door: $$ v = \sqrt{gd} $$ Hier is g de valversnelling en d de diepte van de zee. 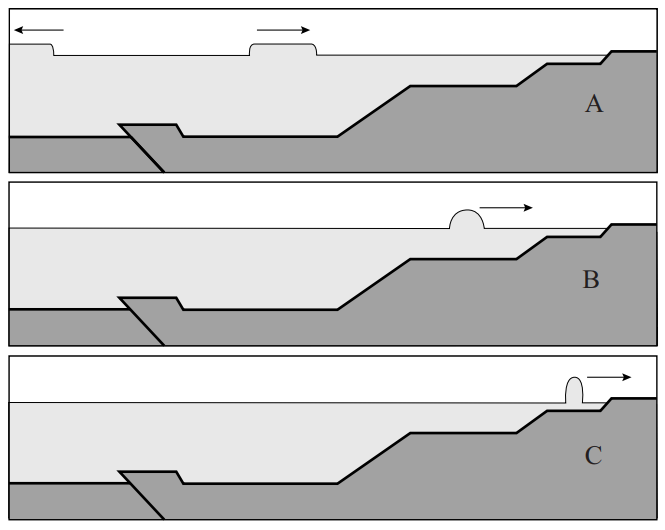In de bovenstaande afbeelding is te zien dat de golf smaller en hoger wordt als het de kust nadert. Verklaar dit effect met behulp van de formule. (bron: examen VWO 2014-1) Hieronder is het (u,x)-diagram van een touw afgebeeld. Een leerling heeft een golf in dit touw laten ontstaan door aan de linkerzijde het touw harmonisch op en neer te bewegen met een frequentie van 0,20 Hz. 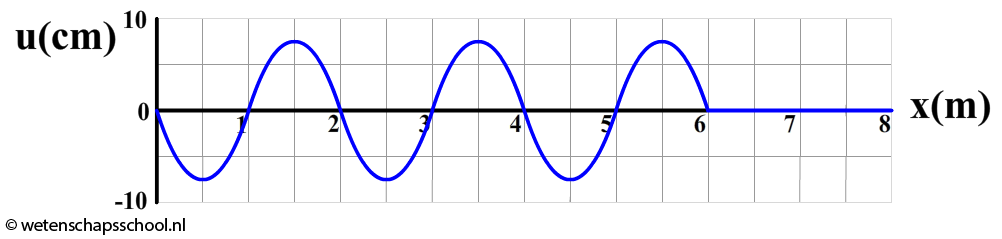(1p) Is de persoon begonnen het touw omhoog of omlaag te bewegen? Licht je antwoord toe. (1p) Leg uit in welke richting het touw op punt x = 3,0 m zal bewegen na het moment weergegeven in het bovenstaande (u,x)-diagram. (1p) Hoeveel trillingen heeft punt x = 5,0 m uitgevoerd? (1p) Leg uit dat punt x = 5,5 meter dezelfde amplitude heeft als punt x = 5,7 m. (3p) Teken het (u,t)-diagram behorende bij punt x = 4,0 m. Geef in het diagram duidelijk aan op welk tijdstip de grafiek stopt. Hieronder zien we het (u,x)-diagram van een touw. Een leerling heeft een golf in dit touw laten ontstaan met een frequentie van 0,50 Hz door aan de linkerzijde het touw op en neer te bewegen. 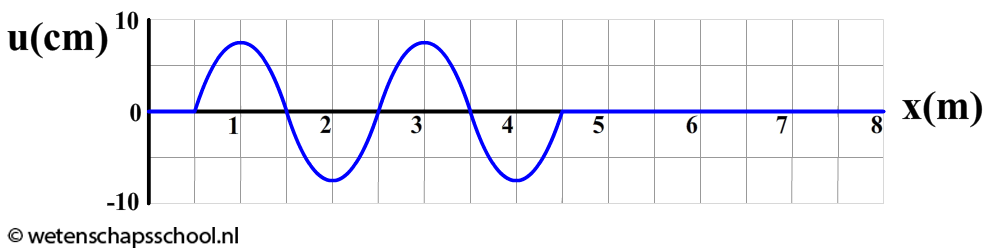(3p) Teken het (u,t)-diagram behorende bij punt x = 0 m tot aan het moment weergegeven in het bovenstaande (u,x)-diagram. Geef in het diagram duidelijk aan op welk tijdstip de grafiek stopt. (3p) Doe hetzelfde voor punt x = 2,0 m.

 

§5     Faseverschil (VWO)

In deze paragraaf introduceren we het begrip faseverschil. We kunnen hiermee o.a. achterhalen of twee golven of trillingen synchroon lopen of niet. In de volgende paragraaf zullen we nog meer toepassingen zien van dit begrip.

In de onderstaande afbeelding zien we een speaker die een toon met een vaste frequentie voortbrengt en twee microfoons A en B met de bijbehorende oscilloscoopbeelden. In de linker afbeelding bevinden de microfoons zich op dezelfde afstand van de geluidsbron en als gevolg lopen de trillingen op het oscilloscoopbeeld gelijk. We zeggen in zo'n geval dat de trillingen in fase lopen en we zeggen dan dat het faseverschil (Δφ) tussen de trillingen nul is. Wiskundig schrijven we dit als:

$$\Delta \phi = 0$$

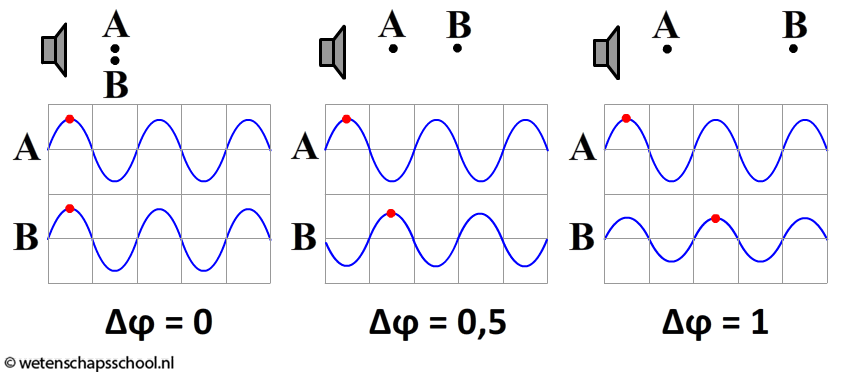
In de middelste afbeelding is microfoon B een stuk naar rechts verschoven. De geluidsgolf komt hier nu later aan. De grafiek behorende bij B is daarom ook een stuk naar rechts verschoven. We zien aan het oscilloscoopbeeld van B dat op deze afstand de trilling een halve trillingstijd achterloopt. Als gevolg is het faseverschil nu gelijk aan:

$$\Delta \phi = 0,5$$

De trillingen lopen nu precies tegengesteld aan elkaar. Als de ene grafiek omhoog gaat, dan gaat de ander naar beneden. We zeggen dat deze trillingen in tegenfase lopen.

In de laatste afbeelding hebben we microfoon B zover doorgeschoven dat de trillingen weer in fase lopen (het faseverschil is hier Δφ = 1). Het enige verschil tussen de oscilloscoopbeelden is nu dat de amplitude bij B iets kleiner is geworden, omdat B zich iets verder van de bron bevindt. Microfoon B loopt nu precies één trillingstijd achter op microfoon A en als gevolg weten we dat er dus een hele golf tussen A en B past. Door de afstand tussen A en B te meten, weten we dus direct wat de golflengte van het geluid is!

Demonstratievideo

In het rechter filmpje wordt dit experiment gedemonsteerd. We gaan hier met het faseverschil niet alleen de golflengte van geluid bepalen, maar ook de geluidssnelheid: DEMO-VIDEO: Faseverschil

Als we de tweede microfoon B nog verder zouden schuiven, dan zouden de twee trillingen op een gegeven moment weer in tegenfase zijn en dan weer in fase etc. Over het algemeen geldt:

$$\Delta \phi = n \;\;\;\; \text{(in fase)} $$ $$\Delta \phi = n+\frac{1}{2} \;\;\;\; \text{(in tegenfase)} $$ $$\text{n = 0, 1, 2, 3, 4 ...} $$

We kunnen het faseverschil in dit experiment ook uitrekenen met een formule:

$$\frac{\Delta t}{T} = \Delta \phi $$ Tijdverschil (Δt) seconde (s) Trillingstijd (T) seconde (s) Faseverschil (Δφ) -

Δt is hier het tijdsverschil tussen de aankomst van de golf bij de twee microfoons.

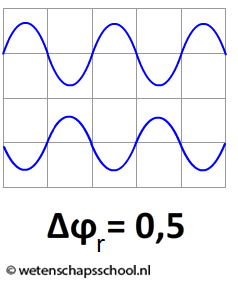
Het vergelijken van twee oscilloscoopbeelden is in principe niet genoeg om het faseverschil te vinden. Kijk bijvoorbeeld naar de volgende afbeelding. Het is hier niet duidelijk of het faseverschil 0,5 is of 1,5 of 2,5 etc. We weten alleen dat het faseverschil eindigt op ",5". We zeggen daarom dat het gereduceerde faseverschil (Δφ_r) hier gelijk is aan 0,5. Het gereduceerde faseverschil is dus het faseverschil waar alle hele getallen vanaf zijn getrokken. Als het faseverschil bijvoorbeeld 8,25 is, dan is het gereduceerde faseverschil 0,25. Als het faseverschil 3,3 is, dan is het gereduceerde faseverschil 0,3.

Leerdoelen:

Zorg dat je weet dat het faseverschil (Δx) vertelt hoeveel twee trillingen of golven uit fase lopen. Als twee trillingen of twee golven synchroon lopen, dan zijn deze trillingen of golven in fase. Als ze precies tegengesteld bewegen, dan zijn ze in tegenfase. Zorg dat je weet dat twee trillingen of golven in fase lopen als "Δφ = n" en in tegenfase lopen als "Δφ = n + 1/2", waarbij n = 0,1,2,3,... Zorg dat je kan rekenen met het faseverschil met behulp van de formule "Δt/T = Δφ". Zorg dat je weet dat het gereduceerde faseverschil (Δφr) gelijk is aan het faseverschil, maar alleen dan met een "0" voor de komma.

Opdrachten

(2p) Een leerling sluit twee microfoons aan op een oscilloscoop en zet een speaker aan die een toon met een vaste frequentie produceert. De oscilloscoopbeelden laten twee grafieken zien die in tegenfase lopen. Leg uit waarom je niet genoeg informatie hebt om het faseverschil tussen de microfoons te bepalen, maar wel het gereduceerde faseverschil. (4p) Een leerling wil de geluidsnelheid bepalen met de volgende opstelling. Twee microfoons worden op dezelfde afstand van een geluidsbron geplaatst. Een van de microfoons wordt dan 113 cm verder van de speaker geplaatst. Op deze plek lopen de trillingen voor het eerst in tegenfase. De speaker produceert een geluid met een frequentie van 150 Hz. Bereken de geluidsnelheid. Hieronder is schematisch een bron weergegeven die geluidsgolven uitzendt. De ruimte waarin deze golven zich verplaatsen is gevuld met koolstofdioxide. 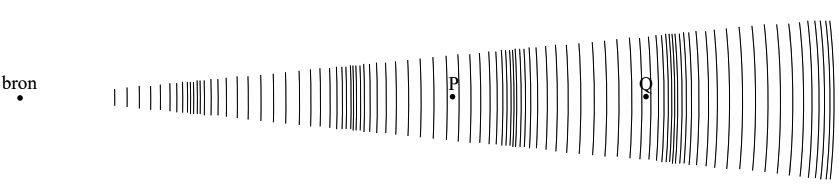In de punten P en Q wordt het geluid waargenomen met behulp van twee microfoons die aangesloten zijn op een oscilloscoop. 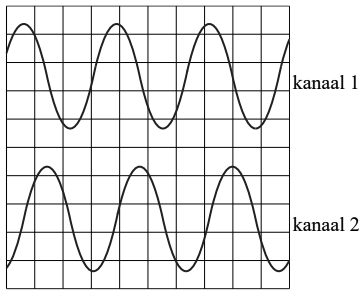Dit levert het volgende beeld op: De tijdbasis van de oscilloscoop is ingesteld op 0,50 ms/hokje. (4p) Bepaal de frequentie van het waargenomen geluid. (2p) De amplitude van het geluid in P is verschillend van de amplitude van het geluid in Q. Toch zijn de amplitudes op het oscilloscoopbeeld gelijk. Dat komt omdat de gevoeligheid in mV/hokje van de twee kanalen anders is ingesteld. Leg uit of de gevoeligheid van het kanaal van de microfoon in P groter of kleiner is dan de gevoeligheid van het kanaal van de microfoon in Q. (2p) De twee signalen in het oscilloscoopbeeld vertonen een faseverschil. Leg op grond daarvan uit of de microfoon in P aangesloten is op kanaal 1 of op kanaal 2. 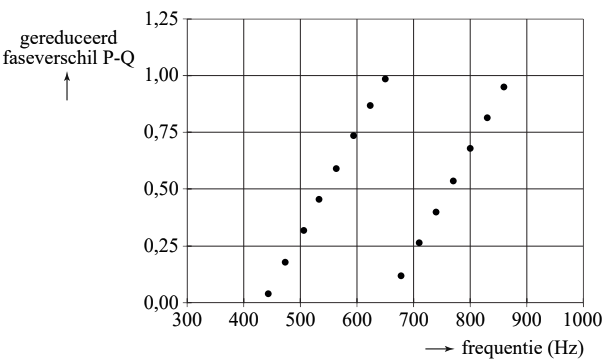(4p) Voor het bepalen van de geluidssnelheid in koolstofdioxide worden de microfoons verplaatst. De afstand tussen P en Q is nu 1,19 m. De frequentie van de geluidsbron is regelbaar. Bij verschillende frequenties wordt het gereduceerde faseverschil tussen P en Q bepaald. Bepaal met dit figuur de geluidsnelheid in koolstofdioxide. (bron: examen VWO 2011-pilot)

 

§6     Interferentie (VWO)

In deze paragraaf gaan we ontdekken wat er gebeurt als meerdere golven door elkaar heen gaan lopen. Op sommige punten zullen de golven elkaar versterken en op andere zullen ze elkaar uitdoven. We spreken hier van interferentie. Om uit te vinden wanneer dit gebeurt hebben we het begrip faseverschil nodig uit de vorige paragraaf.

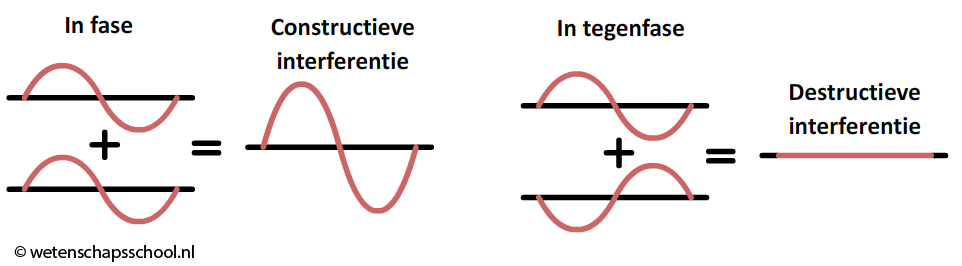
Als twee geluidsgolven door elkaar heen gaan lopen, dan worden de uitwijkingen van de golven bij elkaar opgeteld. Deze "optelling van golven" wordt superpositie genoemd. Op sommige punten zullen de golven elkaar versterken en op andere zullen de golven elkaar uitdoven. We noemen deze effecten interferentie.

Als twee geluidsgolven op een bepaald punt in fase lopen, dan zullen de golven elkaar maximaal versterken en is het geluid maximaal hoorbaar. We spreken hier van constructieve interferentie en we noemen een punt waar dit plaatsvindt ook wel een maximum. Als de geluidsgolven op een bepaald punt in tegenfase lopen, dan zullen ze elkaar opheffen en als gevolg is er geen geluid hoorbaar. We spreken hier van destructieve interferentie en we noemen een punt waar dit plaatsvindt ook wel een minimum.

Demonstratievideo

In het rechter filmpje is dit effect gedemonsteerd met twee speakers. Op sommige plekken is door interfentie veel minder geluid te horen dan op andere plekken. Helemaal stil wordt het in dit experiment nergens, omdat geluid ook nog via de muren en objecten in de ruimte kan reflecteren. DEMO-VIDEO: Interferentie

In de onderstaande afbeelding worden twee geluidsgolven linksom en rechtsom door buizen gestuurd. In de linker afbeelding is het linker en het rechter pad even groot. De geluidsgolven komen daarom in fase aan de bovenkant van het apparaat aan. Als gevolg zullen de golven elkaar hier versterken. Er vindt hier dus constructieve interferentie plaats en het geluid is nu maximaal hoorbaar.

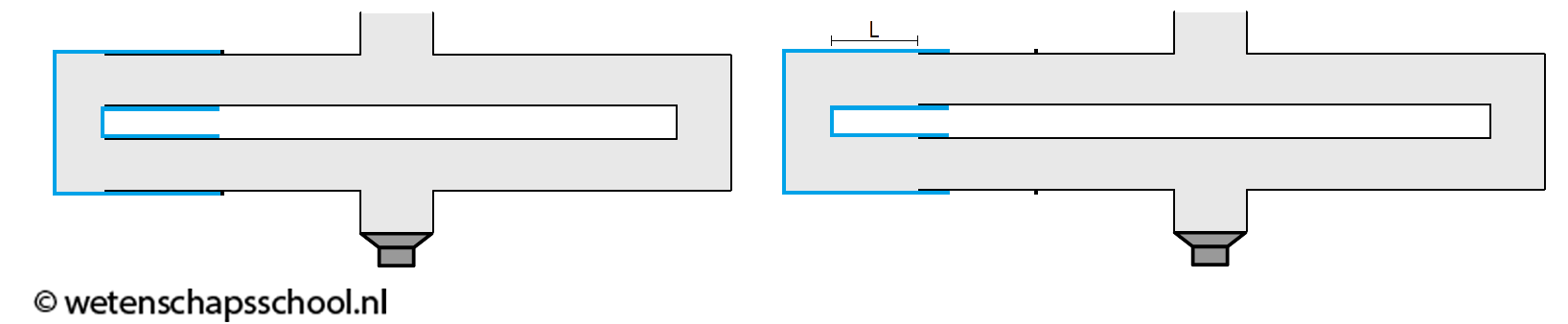
Als we het linker pad geleidelijk verlengen (zie de rechter afbeelding), dan komt er een moment waarop de golven in tegenfase aankomen (Δφ = 0,5). Het linker pad is nu een halve golflengte langer dan het rechter pad. Als gevolg treedt nu destructieve interferentie op en is er geen geluid hoorbaar bij de uitgang (in de praktijk is nog wel een beetje geluid hoorbaar, o.a. doordat het geluid ook door de buizen naar buiten trilt).

Als het linker pad nog verder verlengt wordt, dan komt er een moment dat de golven weer in fase aankomen (Δφ = 1). Het linker pad is nu één golflengte langer dan het rechter pad. Als gevolg treedt nu weer constructieve interferentie op en is het geluid weer maximaal hoorbaar bij de uitgang.

Het verschil in lengte tussen de twee paden noemen we het weglengteverschil (Δx). In formuletaal geldt:

$$\frac{\Delta x}{\lambda } = \Delta \phi$$ Weglengteverschil (Δx) meter (m) Golflengte (λ) meter (m) Faseverschil (Δφ) -

Als er een heel aantal golven in dit weglengteverschil past, dan geldt Δφ = n en vindt er constructieve interferentie plaats. Als geldt dat Δφ = n + 0,5, dan vindt er destructieve interferentie plaats. Er geldt dus:

$$\Delta \phi = n \;\;\;\; \text{(constructief)} $$ $$\Delta \phi = n+\frac{1}{2} \;\;\;\; \text{(destructief)} $$ $$\text{n = 0, 1, 2, 3, 4 ...} $$

Als je op de onderstaande afbeelding klikt, dan opent een programma waarin je zelf geluidsbronnen kan plaatsen en het interferentiepatroon kan zien ontstaan. Op de website vindt je bij deze paragraaf een programma waarin je zelf geluidsbronnen kan plaatsen en het interferentiepatroon kan zien ontstaan. Hieronder zien we twee screenshots van dit programma. Merk op dat er lijnen ontstaan waar destructieve interferentie optreedt. Dit worden de knooplijnen genoemd. Ook heb je lijnen waar constructieve interferentie optreedt. Dit worden de buiklijnen genoemd.

In de onderstaande animatie zijn twee luidsprekers naast elkaar afgebeeld. Het onderstaande figuur is op de website ook als animatie afgebeeld. In de animatie zijn twee luidsprekers naast elkaar afgebeeld. Beide luidsprekers produceren dezelfde toon. De dikke lijnen geven aan op welke plekken de luchtdichtheid het grootst is. De stippellijnen geven aan op welke plekken de dichtheid het kleinst is.

Bij punt A komen telkens golven met hoge dichtheid samen en dan golven met lage dichtheid. Deze golven versterken elkaar en hier treedt dus constructieve interferentie op. Het is deze maximale verandering van dichtheid die ons oor waarneemt als geluid. Bij punt B komt telkens een hoge dichtheidsgolf en een lage dichtheidsgolf tegelijk samen. De golven heffen elkaar hier op en als gevolg is de dichtheid van de lucht hier constant en gelijk aan de waarde die de dichtheid zou hebben als er helemaal geen geluidsgolven zouden zijn. Er treedt hier dus destructieve interferentie op en er is dus (zo goed als) geen geluid te horen. De uitdoving op punt B is goed merkbaar, maar niet perfect. Dit komt o.a. doordat het geluid van de linker bron een grotere afstand heeft moeten afleggen en dus een kleinere amplitude gekregen heeft en omdat de geluidsgolven vaak ook nog reflecteren tegen objecten in de omgeving, waardoor alsnog geluid bij punt B kan aankomen.

Tijd voor een rekenvoorbeeld. In het onderstaande voorbeeld zien we wederom de twee luidsprekers, maar dit keer zijn de golven niet getekend. Beide luidsprekers zenden golven uit met een golflengte van 1,0 cm.

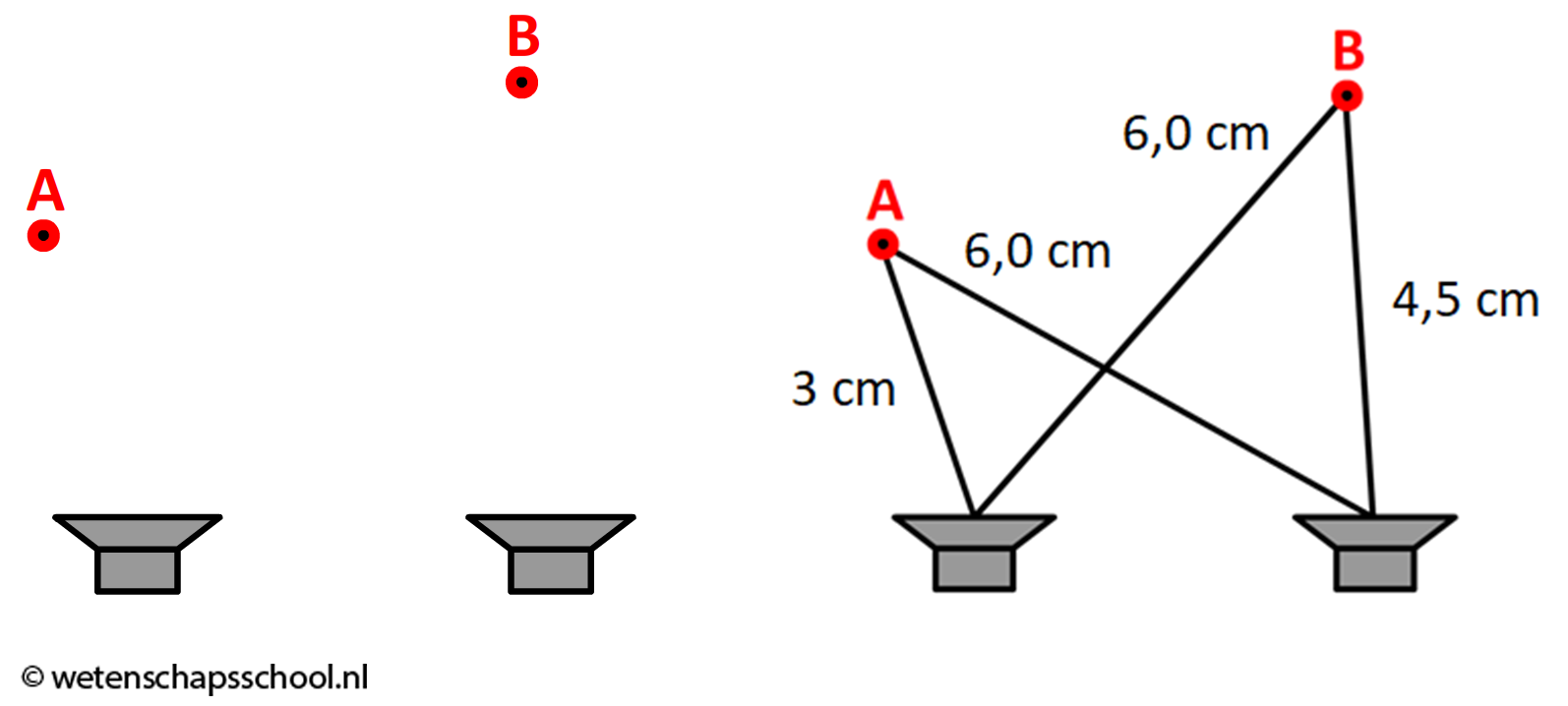
In de rechter afbeelding zijn de afstanden van de geluidsbronnen tot de punten A en B opgemeten. Bij punt A is het weglengteverschil 6,0 - 3,0 = 3,0 cm. Bij punt B is het weglengteverschil 6,0 - 4,5 = 1,5 cm. Met dit weglengteverschil kunnen we het faseverschil uitrekenen:

$$\Delta \phi = \frac{\Delta x}{\lambda}$$ $$\Delta \phi_A = \frac{3,0}{1,0}=3,0 $$ $$\Delta \phi_B = \frac{1,5}{1,0}=1,5 $$

Punt A voldoet aan Δφ = n. Er treedt hier dus constructieve interferentie op. Punt B voldoet aan Δφ = n + 0,5. Hier treedt dus destructieve interferentie op.

Leerdoelen:

Zorg dat je begrijpt dat twee golven in fase elkaar versterken. We noemen dit constructieve interferentie. Twee golven in tegenfase doven elkaar uit. We noemen dit destructieve interferentie. Zorg dat je kan rekenen met "Δx/ λ = Δφ", waarbij "Δx" het weglengteverschil is tussen twee paden die een geluidsgolf genomen heeft. Als in het weglengteverschil een heel aantal golven past (Δφ = n), dan ontstaat constructieve interferentie. Als in het weglengte verschil een heel aantal golven plus een half past (Δφ = n + 1/2), dan ontstaat destructieve interferentie. Als twee cirkelvormige golven met elkaar interfereren, dan ontstaan knooplijnen waar de deeltjes in hun evenwichtsstand blijven (destructieve interferentie, Δφ = n + 1/2) en buiklijnen waar deeltjes maximaal trillen (constructieve interferentie, Δφ = n). Als de twee bronnen een toon uitzenden in tegenfase, dan draait het patroon van constructieve en destructieve interferentie om.

Opdrachten

Een luidspreker wordt bevestigd aan een serie buizen. Aan de linkerkant kan de lengte van de buizen aangepast worden. Als de buis geheel ingeschoven is, dan zijn beide paden even lang. De luidspreker produceert een toon met een frequentie van 440 Hz. (2p) Leg uit of het geluid aan de bovenkant van de buizen versterkt of verzwakt te horen is als de buis geheel ingeschoven is. (5p) Bereken de afstand L dat de buis uitgeschoven moet worden om het eerste minimum te vinden. Ga ervan uit dat de temperatuur van de lucht in de buizen gelijk is aan 20 graden Celsius. In de onderstaande afbeelding zijn twee luidsprekers weergegeven die dezelfde toon in fase produceren. 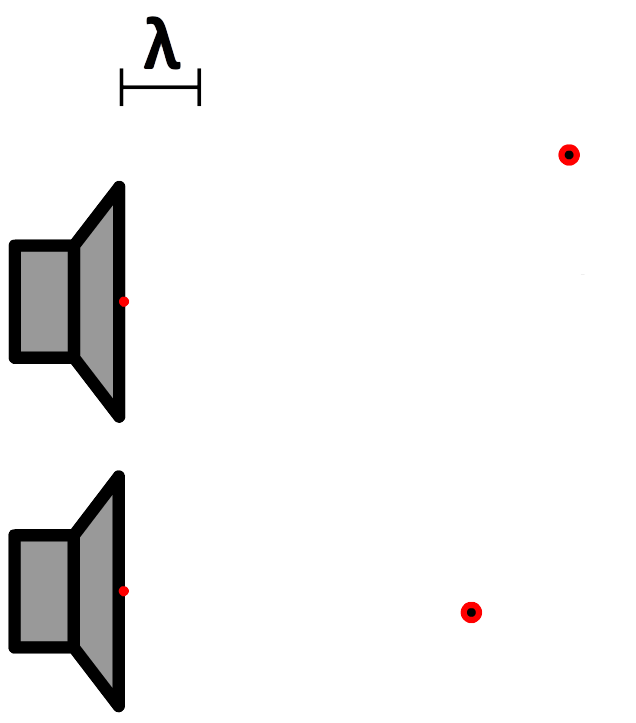(2p) Geef voor elk van de twee rode punten aan of er een minimum of een maximum bevindt. (2p) Als je dit experiment in werkelijkheid uitvoert dan zou je op een minimum toch een beetje geluid horen. Geef hiervoor twee redenen. (1p) Teken de buiklijnen in de tekening. (1p) Teken de knooplijnen in de tekening. In de onderstaande afbeelding zien we een golf in een waterbak die op een muurtje afkomt met daarin twee openingen. De afstand tussen de lijnen in de tekening is gelijk aan een hele golflengte. Bij beide openingen zullen cirkelvormige golven ontstaan. 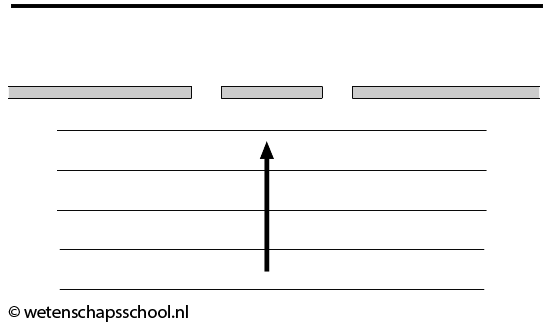De golven komen op den duur aan bij de zwarte horizontale streep aan de bovenkant van de afbeelding. (3p) Geef drie punten aan op deze streep waar de golven elkaar maximaal versterken. (1p) Leg uit of het wateroppervlak zijn laagste punt bereikt bij de minima of de maxima. Leg je antwoord uit. In de onderstaande afbeelding zijn twee luidsprekers weergegeven die dezelfde toon in fase produceren. 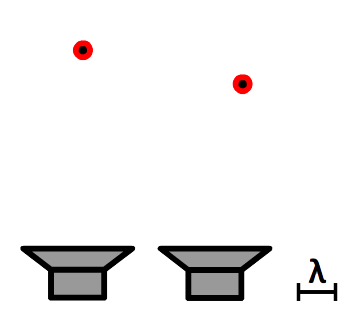(4p) Geef voor beide punten het faseverschil en het gereduceerde faseverschil. (2p) Leg voor elk van de twee aangegeven punten uit of er een minimum of een maximum bevindt. (1p) Beantwoord vraag a en b voor de situatie waarbij de luidsprekers twee tonen in tegenfase produceren. Twee luidsprekers L1 en L2 hebben een onderlinge afstand van 3,00 m (zie de onderstaande afbeelding). De twee luidsprekers zijn in fase aangesloten op een toongenerator die een pure toon produceert. De afbeelding is niet op schaal weergegeven. 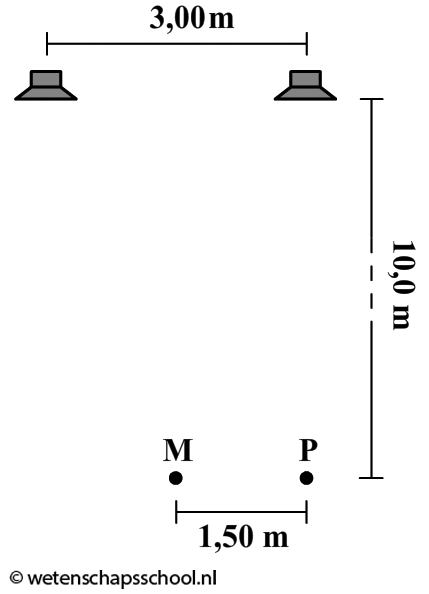(1p) Leg uit dat in punt M de bronnen elkaar versterken. (6p) Een persoon loopt met een microfoon van M naar P. Bij P vindt hij voor de tweede keer een minimum. Bereken met deze informatie de frequentie van het geluid. Ga ervan uit dat de temperatuur van de lucht gelijk is aan 20 graden Celsius. (1p) Leg uit waarom er op punt P geen volledige stilte heerst. Je mag er van uitgaan dat reflectie-effecten verwaarloosbaar zijn. Een leerling wil de golflengte en de frequentie van een bepaald type laserlicht bepalen. Hij gebruikt hiervoor een interferometer (zie de onderstaande afbeelding). In dit apparaat wordt licht met een bepaalde frequentie tegen een halfdoorlaatbare spiegel geschoten. Deze spiegel laat de helft van het licht door en reflecteert de andere helft. Uiteindelijk komen beide lichtstralen weer samen in een detector. 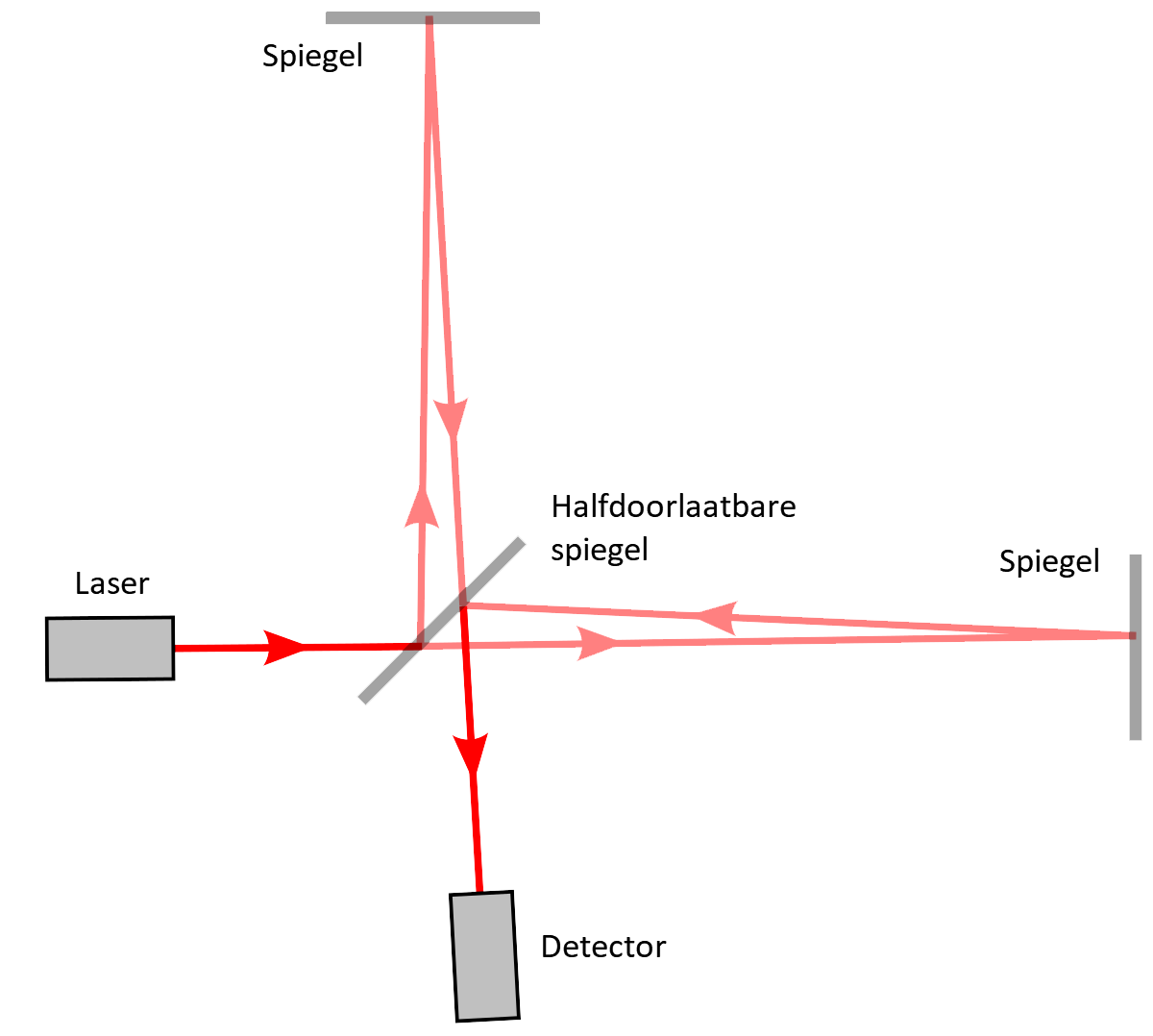(Afbeelding: Krishnavedala; CC BY-SA 4.0) Als de spiegels op gelijke afstand staan, dan leggen beide lichtstralen een gelijke afstand af en versterken ze elkaar bij de detector. (5p) Met een speciaal systeem kan de spiegel met 0,01 μm nauwkeurig verplaatst worden. Het blijkt met dit systeem dat het eerste minimum bereikt wordt als de rechter spiegel 0,16 μm naar rechts wordt geschoven. Bereken met deze informatie de golflengte van dit laserlicht in nm. Zoek daarna met behulp van BINAS op om welke kleur licht het hier gaat. (2p) Stel dat de onderzoekers de spiegel in één keer 1,0 cm naar rechts hadden verplaatst en dat op deze afstand ook een minimum had plaatsgevonden. Leg uit dat je in dat geval niet genoeg informatie hebt om de golflengte van het licht te bepalen. Gebruik in je antwoord in ieder geval het woord faseverschil en gereduceerde faseverschil. (6p) Een wetenschapper bedenkt een methode waarbij vliegtuigen nauwkeurig kunnen landen bij mist en hevige regen. Twee radiozenders worden hiervoor aan het einde van de landingsbaan geplaatst op een onderlinge afstand van 50 m, zoals hieronder van bovenaf is weergegeven (de afbeelding is niet op schaal). 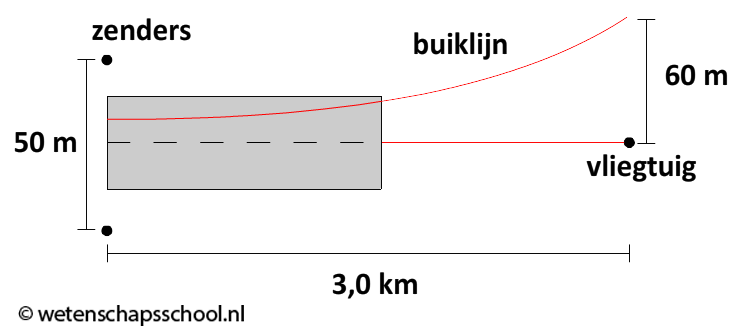De radiozenders zenden in tegenfase twee golven uit met dezelfde frequentie. Op deze manier treedt op de middellijn van de landingsbaan destructieve interferentie op. Als het vliegtuig zich op deze lijn bevindt, zal het dus geen signaal ontvangen. Als het vliegtuig te veel naar links of rechts afwijkt, dan zal het vliegtuig wel een signaal ontvangen en weet de piloot dat hij moet bijsturen. Om genoeg nauwkeurig te zijn moeten de eerste buiklijnen zich op 60 meter aan beide zijde van de middellijn bevinden op een afstand van 3,0 km van de zenders (zie wederom de afbeelding). Bereken op welke frequentie de zenders ingesteld moeten worden.

 

§7     Staande golven

In deze paragraaf gaan we muziekinstrumenten bestuderen. In muziekinstrumenten ontstaan zogenaamde staande golven. In deze paragraaf gaan we deze golven leren beschrijven met tekeningen en formules.

In de onderstaande animatie zijn twee dezelfde golven te zien die in tegengestelde richting bewegen. In de animatie op de website zijn twee dezelfde golven te zien die in tegengestelde richting bewegen. De individuele golven zijn in het rood en het blauw aangegeven. De superpositie van de twee golven is weergegeven in het zwart. De golf die ontstaat beweegt niet naar links en niet naar rechts en is dus geen lopende golf. We noemen dit type golf een staande golf. Zoals je kunt zien staan sommige punten van het touw de gehele tijd stil. Deze punten noemen we knopen. Andere punten in het touw bewegen maximaal omhoog en naar beneden. We noemen dit buiken.

Een staande golf ontstaat bijvoorbeeld op als we een golf heen en weer laten bewegen in een kleine ruimte. De golf reflecteert dan tegen de uiteinden van deze ruimte en komt zichzelf tegen, waardoor een staande golf ontstaat. Hieronder zien we bijvoorbeeld drie staande golven in een snaar die aan beide kanten vast zit. De knopen zijn weergegeven met de letter K en de buiken met de letter B. Zoals je in de afbeelding kunt zien is de afstand tussen een buik en een knoop gelijk aan een kwart golflengte.

Demonstratievideo

Hieronder zien we deze staande golven onstaan in een touw: DEMO-VIDEO: Staande golven I DEMO-VIDEO: Staande golven II

De eerste staande golf noemen we de grondtoon. De andere tonen die zijn afgebeeld noemen we de boventonen. We geven deze verschillende tonen ook aan met een nummer. Voor de grondtoon geldt n = 1. Voor de eerste boventoon schrijven we n = 2. Voor de tweede boventoon geldt n = 3. Etc. Zoals je kunt zien bevat de grondtoon een buik en twee knopen. Elke daaropvolgende toon bevat telkens één extra knoop en één extra buik. In een muziekinstrument is de grondtoon meestal het duidelijkst te horen.

Zoals je kunt zien past er bij de grondtoon een halve golflengte in de snaar. De snaar in de eerste boventoon bevat een hele golflengte. De snaar in de tweede boventoon bevat anderhalve golflengte, etc. We kunnen dit patroon samenvatten met de volgende formule:

$$L=n\frac{1}{2}\lambda \;\;\;\; \textbf{(twee vaste uiteinden)}$$ Lengte trillend voorwerp meter (m) Nummer toon (n) 1, 2, 3, … Golflengte (λ) meter (m)

Als we de frequentie van de grondtoon f₁ weten, dan kunnen we de daaropvolgende frequenties als volgt vinden:

$$f_n = n \times f_1 \;\;\;\; \textbf{(twee vaste uiteinden)}$$

In de volgende afbeelding zien we trillingen in een snaar die aan beide kanten vrij kan bewegen. Bij dit type staande golf hebben we dus aan beide uiteinden een buik.

Ook in dit geval bestaat de grondtoon uit een halve golflengte, de eerste boventoon uit een hele golflengte, etc. Ook hier gelden dus dezelfde formules:

$$L=n\frac{1}{2}\lambda \;\;\;\; \textbf{(twee losse uiteinden)}$$ $$f_n = n \times f_1 \;\;\;\; \textbf{(twee losse uiteinden)}$$

In het derde geval zit de snaar aan één kant vast en aan de andere kant los. In dit geval hebben we dus aan de ene kant altijd een buik en aan de andere kant altijd een knoop.

De grondtoon bevat slechts één buik en één knoop. Er zit nu slechts een kwart golf in het touw. Bij de eerste boventoon zien we twee knopen en twee buiken. In dit geval past er dus driekwart van een golf in het touw. Etc. We kunnen dit patroon samenvatten met de volgende formule:

$$L = (2n-1)\frac{1}{4}\lambda \;\;\;\; \small{\textbf{(een los en een vast uiteinde)}}$$ Lengte trillend voorwerp meter (m) Nummer toon (n) 1, 2, 3, … Golflengte (λ) meter (m)

In dit geval geldt:

$$f_n = (2n-1) \times f_1 \;\;\;\; \small{\textbf{(een los en een vast uiteinde)}}$$

Ook in lucht kunnen we staande golven creëren. Hieronder zien we animaties van staande golven in lucht in een buis met twee open uiteinden en een buis met een open en een gesloten uiteinde.Op de website kan je animaties vinden van staande golven in lucht in een buis met twee open uiteinden en een buis met een open en een gesloten uiteinde. Aan de open uiteinden kan de lucht vrij bewegen. Hier hebben we dus te maken met een buik. Aan een gesloten uiteinde staat de lucht stil. Hier hebben we dus te maken met een knoop. We krijgen hier dezelfde patronen van buiken en knopen als bij staande golven in een touw.

Demonstratievideo

In het rechter filmpje worden staande golven gevormd in een luchtkolom die aan de onderkant gesloten is. Het ontstaan van een staande golf is goed te horen omdat dan de amplitude van het geluid enorm toeneemt (dit is ook een vorm van resonantie). Volgens de formule L = (2n-1) × 1/4 × λ gebeurt dit bij een 1/4 golflengte, 3/4 golflengte, 5/4 golflengte, etc. DEMO-VIDEO: Staande golven in luchtkolom

Voorbeeld

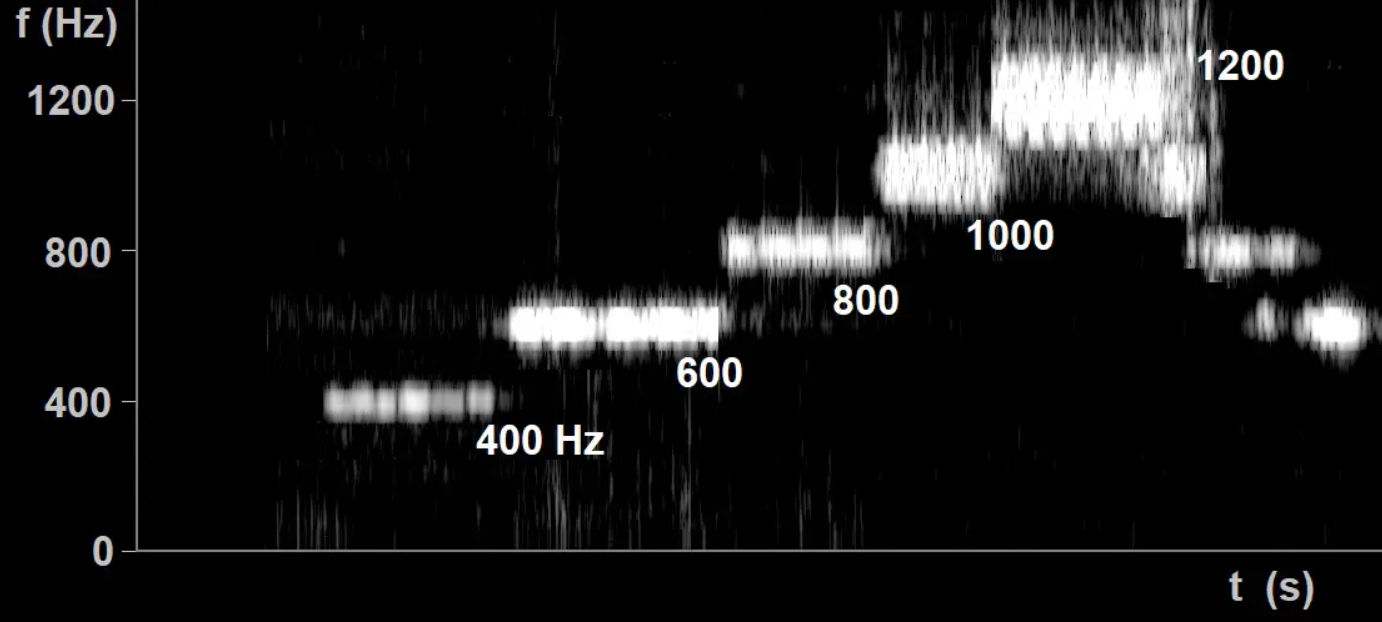
Vraag: In de onderstaande rechter afbeelding zien we een zogenaamde slingerbuis. Als je deze buis rondslingert zijn bij bepaalde snelheden tonen te horen. Deze tonen komen overeen met de boventonen (de grondtoon is in deze buis amper hoorbaar). In de linker afbeelding zien we de frequentie van de tonen die met de buis geproduceerd kunnen worden. Teken in de rechter afbeelding het knopen-en-buikenpatroon dat hoort bij de toon met een frequentie van 800 Hz. Antwoord: De grondtoon is niet zichtbaar. 400 Hz is dus de eerste boventoon, 600 Hz de tweede boventoon en 800 Hz de derde boventoon. Bij een buis die aan beide kanten open is geldt bij de derde boventoon (n = 4) dat er vier knopen tussen de uiteinden van de buis zitten (zie de onderstaande afbeelding).

VWO-STOF

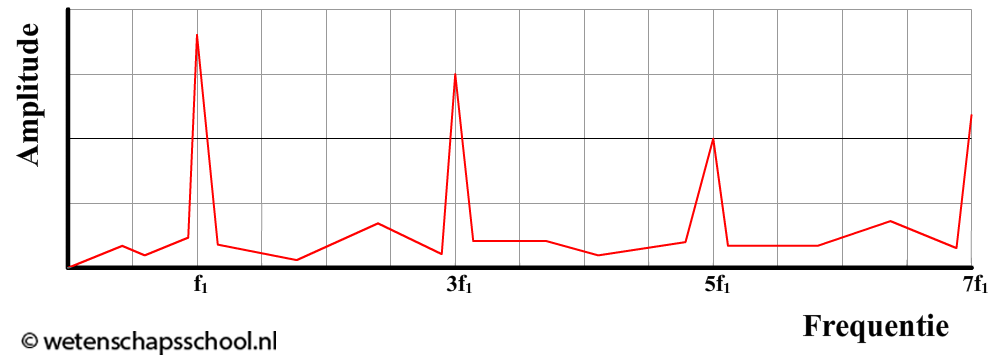
Als we in de praktijk een toon produceren met een muziekinstrument, dan horen we meestal een complexe combinatie van de grondtoon en de boventonen. Hieronder zien we bijvoorbeeld het geluidspectrum van een fluit. De eerste piek die we zien is de grondtoon en de rest van de pieken zijn de boventonen. De positie en de hoogte van deze pieken verklaart het verschil tussen het geluid van bijvoorbeeld een fluit, een trompet of een gitaar. 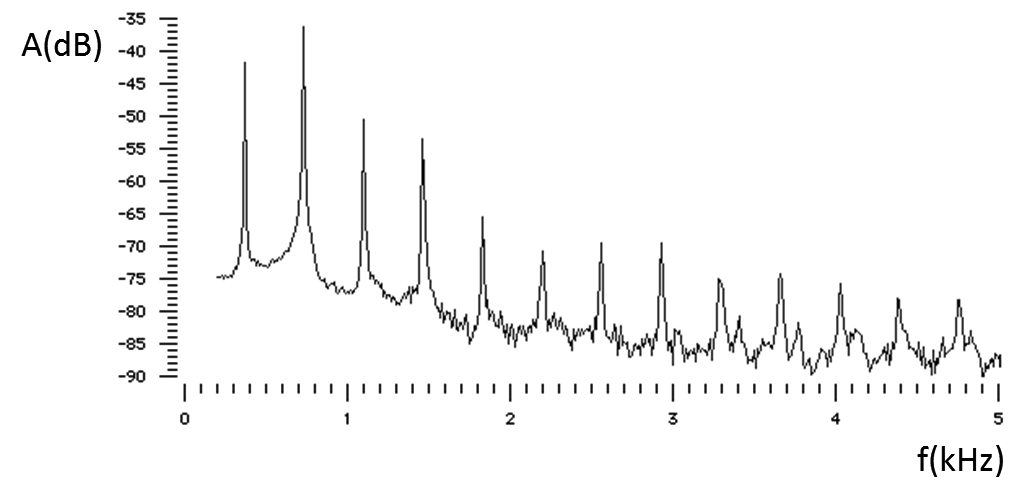In de bovenstaande grafiek zien we dat alleen bij bepaalde frequenties de geluidsterkte dramatisch toeneemt. Waar hebben we dit eerder gezien? Dit is resonantie! De pieken zijn dus resonantiepieken en dit verklaart waarom muziekinstrumenten een goed hoorbare toon kunnen voortbrengen. In de onderstaande animatie kan je zien hoe een golf in een snaar eruit ziet als we de grondtoon en de boventonen combineren.

Leerdoelen:

Zorg dat je weet dat bij staande golven sommige punten stilstaan. Dit noemen we knopen (K). Sommige punten trillen maximaal. Dit noemen we de buiken (B). Zorg dat je weet dat bij staande golven de afstand tussen een buik en een knoop gelijk is aan een kwart golflengte. Zorg dat je de grondtoon (n = 1) en de boventonen van een snaar die aan beide kanten vastzit kan tekenen. Zorg ook dat je hiermee kan rekenen met behulp van de formules "L = 1/2nλ" en "fn = nf1". Zorg dat je de grondtoon (n = 1) en de boventonen van een snaar die aan beide kanten los zit kan tekenen. Zorg ook dat je hiermee kan rekenen met behulp van de formules "L = 1/2nλ" en "fn = nf1". Zorg dat je de grondtoon (n = 1) en de boventonen van een snaar die aan één kant vastzit kan tekenen. Zorg ook dat je hiermee kan rekenen met behulp van de formules "L = (2n-1)1/4λ" en "fn = (2n-1)f1". Zorg ook dat je de patronen van buiken (B) en knopen (K) kan tekenen bij staande geluidsgolven. Zorg dat je weet dat n = 2 de eerste boventoon is, n = 3 de tweede boventoon, etc. (VWO) Zorg dat je weet dat pieken in een geluidsspectrum worden veroorzaakt door resonantie en overeenkomen met de grondtoon en de boventonen.

Opdrachten

(1p) Leg uit hoe groot de afstand is tussen een knoop en een buik bij een staande golf, uitgedrukt in de golflengte. (3p) Teken het patroon van buiken en knopen bij een gitaarsnaar, bij een panfluit met twee open uiteinden en bij een panfluit met één gesloten uiteinde. Doe dit voor de grondtoon en de eerste twee boventonen. Gebruik de letter K om een knoop aan te duiden en de letter B om een buik aan te duiden. Een aantal leerlingen staan op een loopbrug en bewegen ritmisch op en neer met een bepaalde frequentie. Als gevolg komt de hele brug in trilling en ontstaat er een staande golf (zie de onderstaande afbeelding). (3p) De lengte van de brug is 28 m en de leerlingen bewegen op en neer met een frequentie van 0,56 Hz. Bereken de voortplantingssnelheid van de lopende golven in de brug. (3p) De studenten gaan nu met een frequentie van 1,12 Hz op en neer bewegen. Teken de uiterste standen van de staande golf die hierbij ontstaat. Licht je tekening toe met een berekening of een redenering. (bron: examen HAVO 2011-1) Het geluid van een stemvork wordt vaak versterkt door deze op een klankkast te zetten die aan de ene kant gesloten is en aan de andere kant open. Een bepaalde klankkast heeft een lengte van 17,8 cm en de lucht in de klankkast gaat in zijn grondtoon trillen. (5p) Bereken de frequentie behorende bij deze grondtoon. Ga er van uit dat de temperatuur van de lucht in de klankkast 20 graden Celsius is. (2p) De buik die ontstaat aan het open uiteinde van de klankkast bevindt zich eigenlijk iets buiten de opening. Heeft de stemvork in dat geval een grotere of een kleinere frequentie dan berekend bij vraag a. Licht je antwoord toe. In een mondharmonica zit een rij met gaatjes. Onder elk gaatje zit een metalen lipje van verschillende lengte. Een lipje is een dun koperen stripje dat aan één kant is vastgemaakt. Het andere uiteinde kan vrij trillen. Het zijaanzicht van een lipje is hieronder weergegeven. Als een speler lucht door een gaatje blaast, ontstaat in het bijbehorende lipje onder dat gaatje een staande golf. 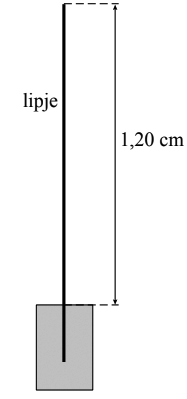(4p) Als het lipje in de grondtoon trilt, ontstaat een toon van 392 Hz. Bereken de voortplantingssnelheid van de golven in het lipje. (3p) Met behulp van een microfoon worden twee geluidsopnames gemaakt waarbij een persoon door twee verschillende gaten blaast. 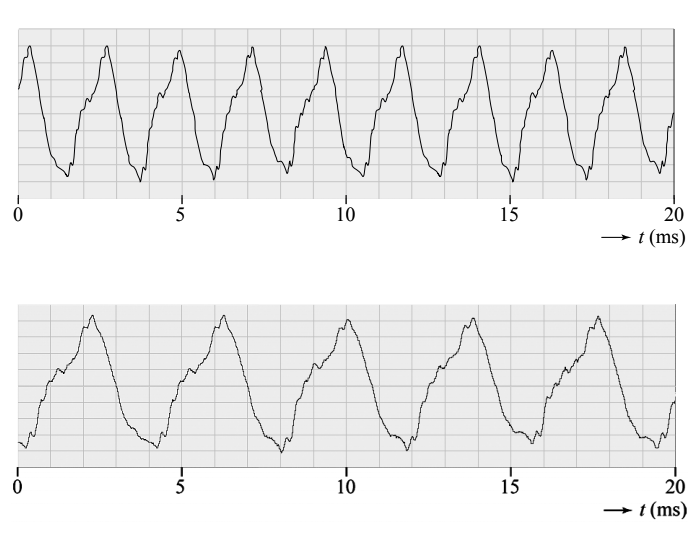Van deze twee opnames zijn de volgende (u,t)-diagrammen gemaakt: Leg uit welke van deze figuren correspondeert met het langste lipje. (1p) Naast de grondtoon gaat het lipje (zeker bij hard blazen) ook trillen in de eerste boventoon. Geef in een tekening weer op welke plaatsen zich buiken en knopen bevinden als het lipje in de eerste boventoon trilt. (bron: examen VWO 2009-1) Een leerling maakt zelf een panfluit bestaande uit buizen van verschillende lengte. Als zij over een buis blaast, gaat de lucht in deze buis trillen en ontstaat er geluid. (3p) Hieronder staan twee zinnen over de geluidsgolven in deze buis. Geef voor elke zin het juiste alternatief: In de buis bevinden zich transversale / longitudinale geluidsgolven met verschillende snelheden / frequenties. Er treedt resonantie op zodra de amplitude / golflengte van een golf in verhouding is met de lengte van de luchtkolom in de buis. (1p) De buizen waar de panfluit uit bestaat zijn aan beide uiteinden open. Teken de knopen (K) en buiken (B) behorende bij de grondtoon. (5p) De buizen worden nu aan de onderkant afgesloten met kurken. De buis heeft een lengte van 18,8 cm. De kurk steekt 1,0 cm in de buis. De temperatuur van de lucht is 20 graden Celsius.  Bereken de frequentie van de grondtoon die de buis dan laat horen. (2p) Bij een meting blijkt de frequentie van de grondtoon hoger dan verwacht. Een leerling denkt dat dit komt omdat de temperatuur van de lucht in de panfluit groter is dan 20 graden Celsius. Kan de hogere temperatuur de oorzaak zijn? (2p) De leerling wil te frequentie verlagen door de kurk dieper of minder diep in de buis te duwen. Leg uit welke kant de kurk op geduwd moet worden. (bron: examen HAVO 2017-2) Als alle gaatjes van een blokfluit dichtgehouden worden, dan produceert de blokfluit een toon met een grondfrequentie van 520 Hz. Je mag ervan uitgaan dat aan beide uiteinden van de blokfluit een buik zit. (4p) Bereken de afstand tussen de twee uiteinden. Ga er van uit dat de temperatuur van de lucht in de blokfluit gelijk is aan 20 graden Celsius. (4p) Het middelste gaatje dat precies halverwege de blokfluit zit, wordt nu geopend. Leg uit welke frequentie de blokfluit nu voortbrengt. (VWO) Een ukelele is een klein formaat gitaar met vier snaren (zie de onderstaande afbeelding). Elke snaar heeft een lengte van 35,0 cm. Alle snaren zijn gemaakt van nylon. Een ukelele kan op verschillende manieren gestemd worden. Een manier van stemmen is hieronder weergegeven: snaar grondtoon f (Hz) 1 G 392 2 C 262 3 E 330 4 A 440 (5p) Laat met behulp van de tabel zien dat de golfsnelheid in de snaren niet gelijk is. (2p) Als snaar 3 en 4 tegelijk worden aangetokkeld, is er een klank te horen die als prettig ervaren wordt. We zeggen ook wel dat deze twee snaren "stemmen". Een verklaring hiervoor is dat deze snaren een of meer gemeenschappelijke boventonen hebben. Bepaal de frequentie van de laagste gemeenschappelijke boventoon van de snaren 3 en 4. (4p) Het verband tussen de spankracht en de golfsnelheid in een snaar kan worden weergegeven met behulp van: $$ v = \sqrt{\frac{F_{span}}{\mu}} \;\;\; \text{met} \; \mu = \frac{m}{l} $$ Hierin is v de golfsnelheid, F de spankracht, m de massa en l de lengte van de snaar. Laat met behulp van deze formule en formules uit BINAS zien dat geldt dat: $$ F_{span} = \frac{\lambda^2f^2\pi d^2 \rho}{4} $$ Hierin is d de dikte van de snaar en ρ de dichtheid van de snaar. (3p) De dikte van snaar 1 bedraagt 0,65 mm. De ukelele is gestemd op de manier zoals weergegeven in de tabel. Bepaal de spankracht in snaar 1. (bron: examen VWO 2015-2) (VWO, 3p) Hieronder zien we het spectrum van een bepaald muziekinstrument met een luchtkolom. Laat met een berekening zien of we hier te maken hebben met een luchtkolom die aan beide kanten open is of dat één kant gesloten is. Een vleugel is een muziekinstrument met toetsen en snaren. Als een toets wordt ingedrukt, slaat een houten hamertje tegen een strak gespannen snaar die vervolgens gaat trillen. De klank die je hoort, bestaat uit de grondtoon en enkele boventonen. (2p) Afhankelijk van de plek waar het hamertje de snaar raakt, zullen de verschillende boventonen wel of niet meeklinken. Stel dat het hamertje neerkomt op 1/8ste deel van de lengte van de snaar. De boventoon die op deze plek een knoop heeft, klinkt dan niet. Noem de laagste boventoon waarbij dit gebeurt. (6p) Niet alle snaren in een vleugel zijn even lang. De snaar die de hoogste toon voortbrengt heeft een lengte van 40 cm. De hoogste toon van de vleugel heeft een grondfrequentie van 4186 Hz. De laagste toon heeft een grondfrequentie van 32,70 Hz. Veronderstel dat alle snaren even strak gespannen zijn, even dik zijn en van hetzelfde materiaal gemaakt zijn. Toon met een berekening aan dat de lengte die de langste snaar dan zou moeten hebben niet in een vleugel past. (7p) De toonhoogte van een snaar hangt, behalve van de lengte, ook af van de spankracht in de snaar. Voor de voortplantingssnelheid v van de golven in de snaar geldt: $$v = \sqrt{\frac{F_{span} l}{m}}$$ Om ervoor te zorgen dat de snaren die de lage tonen moeten voortbrengen toch in de vleugel passen, kun je verschillende maatregelen nemen. Helpt het om de snaar strakker te spannen? En helpt het als we roestvrijstalen snaren vervangen door koperen snaren? Leg je antwoord uit. (bron: examen HAVO 2015-2) Het oor bestaat uit drie gedeeltes: het buitenoor, het middenoor en het binnenoor. Het buitenoor is op te vatten als een buis die aan één kant gesloten is door het trommelvlies. 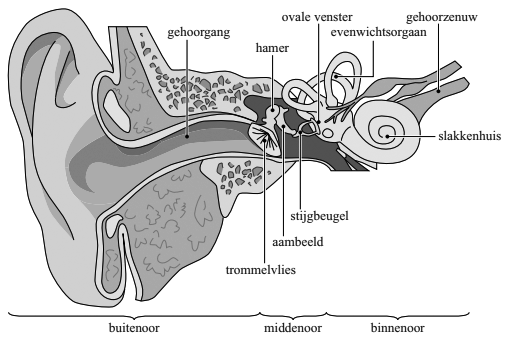(4p) De gehoorgang is bij een volwassen persoon 28 mm lang. Door resonantie wordt geluid met een frequentie van 3 kHz in het buitenoor versterkt. Toon dat aan met behulp van een berekening. (2p) Leg uit of de frequentie waarbij versterking optreedt bij een baby groter of kleiner is dan bij een volwassen persoon. (3p) In het binnenoor zit het slakkenhuis. Hieronder is een tekening gemaakt van het slakkenhuis in uitgerolde toestand. Het is te beschouwen als een met vloeistof gevulde buis met het basilaire membraan als scheidingswand. Op het basilaire membraan zitten kleine massa's, die allemaal een andere eigenfrequentie hebben. 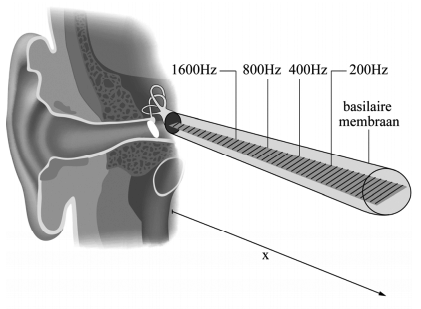Als het ovale venster in trilling gebracht wordt, ontstaat in de vloeistof rondom het basilaire membraan een druktrilling. Leg uit dat bij verschillende tonen, verschillende massa's flink gaan trillen en leg uit hoe het oor op deze manier onderscheid kan maken tussen geluid van verschillende frequenties. (VWO, 4p) De stijfheid van het basilaire membraan is vergelijkbaar met de veerconstante C van een massaveersysteem. De stijfheid van het basilaire membraan verandert met de afstand x tot het ovale venster. 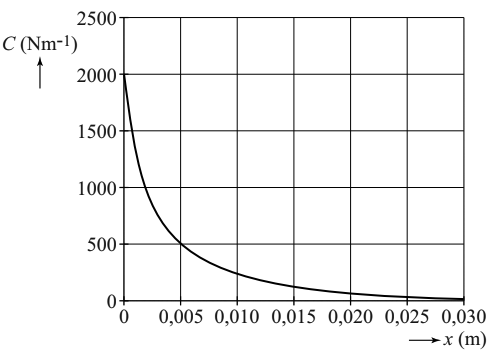Dit is duidelijk te zien in de onderstaande afbeelding: Op een afstand van 5,0 mm van het ovale venster bedraagt de eigenfrequentie 3,0 kHz. Bepaal de massa in het gebruikte model op die plaats van het basilaire membraan. (VWO, 3p) In de afbeelding met het uitgerolde slakkenhuis is te zien dat de frequentie 4 keer kleiner wordt als de afstand (x) verdubbeld. Ga na met welke factor de massa's toenemen bij deze verdubbeling van afstand. (bron: examen VWO 2013-2) (VWO) Een leerling brengt een cirkelvormige metalen lus met een diameter van 24,5 cm in trilling met behulp van een toongenerator (zie de onderstaande linker afbeelding). De plek waar de lus bevestigd is aan het trillingsapparaat kan beschouwd worden als een knoop. Op deze plek ontstaan twee golven die in beide richtingen voortbewegen en uiteindelijk met elkaar interfereren (zie de rechter afbeelding). 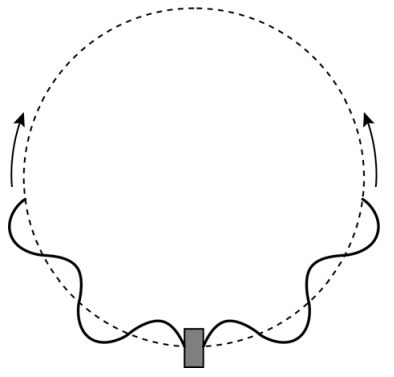(2p) Op basis van deze foto concludeert de leerling dat de golfsnelheid in de lus niet overal gelijk is. Leg uit waarom je deze conclusie kan trekken. (5p) Op het moment dat de foto gemaakt werd, stond de toongenerator ingesteld op 69 Hz. Bepaal de gemiddelde golfsnelheid in de lus bij deze frequentie. (4p) De leerling vindt dat staande golven ontstaan bij de volgende frequenties: Aantal buiken f (Hz) 3 19 5 69 7 1,6 × 102 9 2,6 × 102 11 3,8 × 102 Zoals in de tabel te zien is, is het aantal buiken in de lus telkens oneven. Leg uit hoe dit komt. Beredeneer hiervoor eerst dat aan de bovenkant van de lus altijd een buik te vinden is. (2p) Hieronder is een grafiek te zien van de meetresultaten. 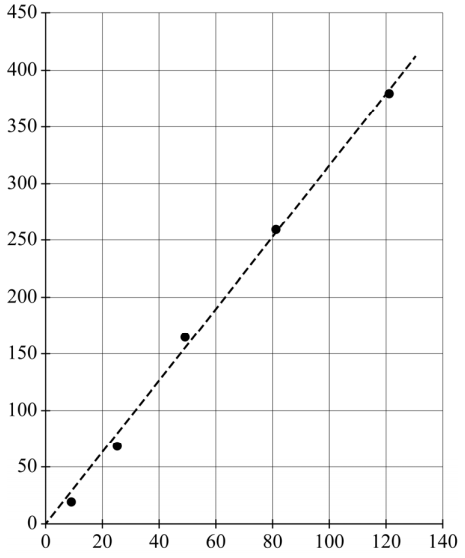Het verband tussen de frequentie (f) en het aantal buiken (n) blijkt te zijn gegeven door: $$ f = cn^2 $$ Schrijf de juiste grootheden en eenheden bij de assen. (3p) Bepaal de grootte van de constante c. Noteer achter je antwoord ook de juiste eenheid. (2p) Geef bij elk van de volgende stellingen aan waarom deze juist of onjuist is: De constante c moet in één significant cijfer gegeven worden (want het aantal buiken is maar in één cijfer gegeven). De constante c mag in drie significante cijfers gegeven worden (desondanks dat de frequentie in de tabel in twee significante cijfers gegeven is). (bron: examen VWO 2021-1) Op sommige plekken op aarde is het verschil tussen eb en vloed zeer groot. De plaats Saint John aan de Fundybaai in Canada is zo'n plaats. 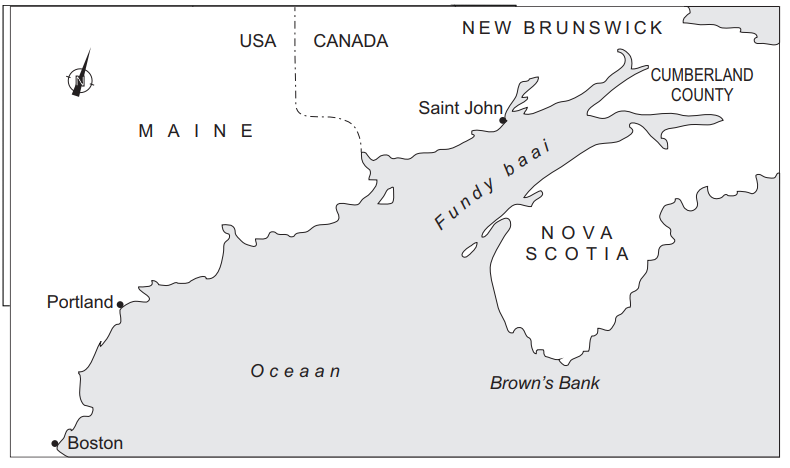De 300 km lange Fundybaai waaraan Saint John ligt, is hieronder weergegeven: Door zijn vorm en afmetingen ontstaat in de Fundybaai een staande golf. Hieronder is het zijaanzicht van deze golf op drie momenten schematisch weergegeven. (5p) Elke 12 uur is het 1x eb en 1x vloed. Bereken op basis van o.a. dit gegeven de golfsnelheid. (3p) Het verschijnsel dat optreedt in de Fundybaai heet getijdenresonantie. Dit verschijnsel treedt op meerdere plaatsen op aarde op. Hieronder zien we de versterkingsfactor van de getijdewerking bij baaien van verschillende lengte L. 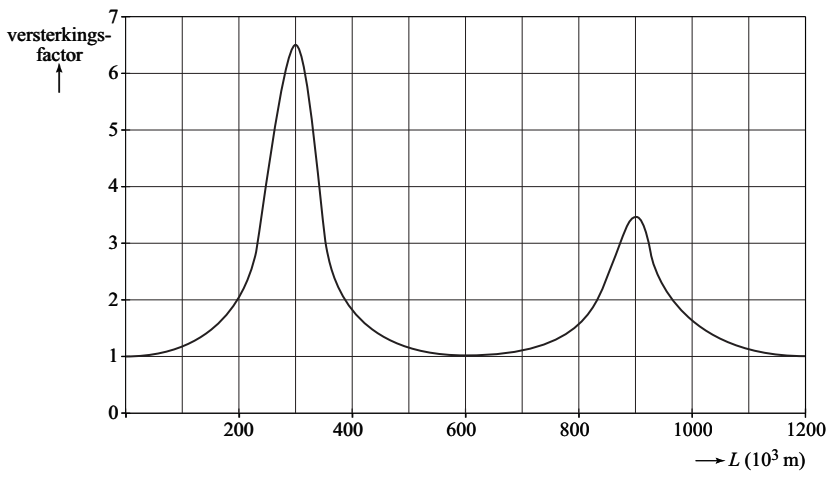Verklaar dat bij een baailengte van 900 km de versterkingsfactor ook hoog is. (bron: examen VWO 2012-1)

BINAS:
15A	Geluidsnelheden
15C	Muzieknoten