Hoofdstuk 4
Optica (keuzemodule HAVO)
§1 Reflectie §2 Breking §3 Het beeld §4 Het virtuele beeld §5 De lenzenformule
§1 Reflectie
In dit hoofdstuk bestuderen we licht. We gaan o.a. bestuderen hoe licht reflecteert en hoe licht van richting verandert als het van de ene naar de andere stof beweegt—dit laatste noemen we breking. Met deze theorie gaan we o.a. de werking van lenzen begrijpen. In de eerste paragraaf beginnen we met reflectie.
Als we een voorwerp zien, dan komt dat doordat licht vanaf dit voorwerp in onze ogen schijnt. Er zijn twee manieren waarop dit kan gebeuren:
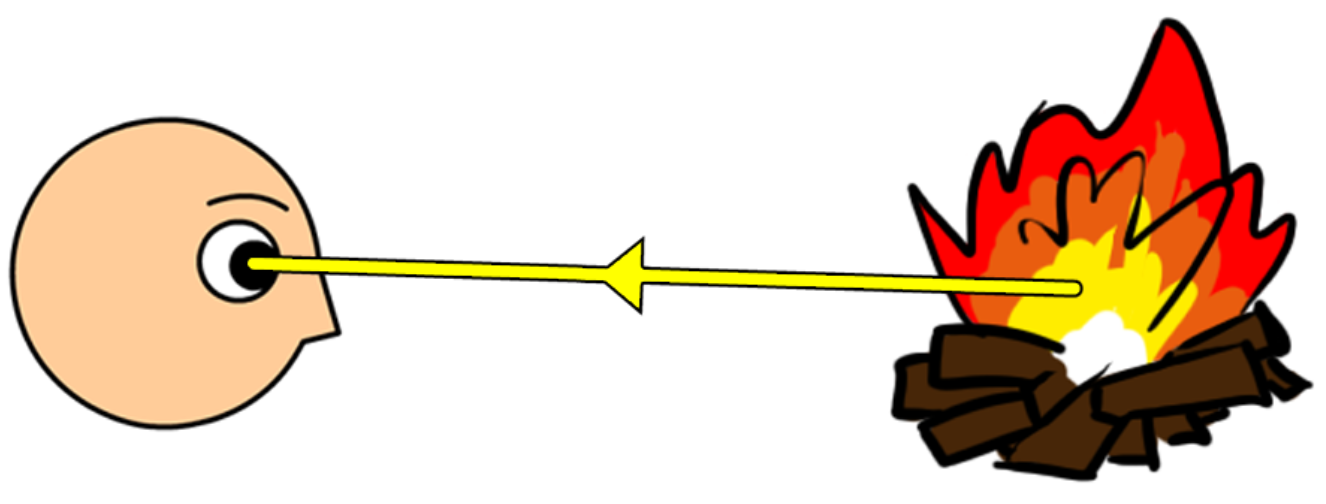
- Een lichtbron is een voorwerp dat licht geeft. Denk bijvoorbeeld aan een lamp, een kampvuur en de zon. We kunnen deze voorwerpen zien als licht vanuit deze lichtbronnen in onze ogen schijnt.
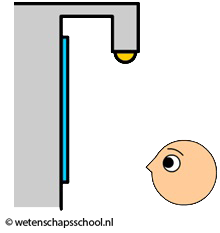
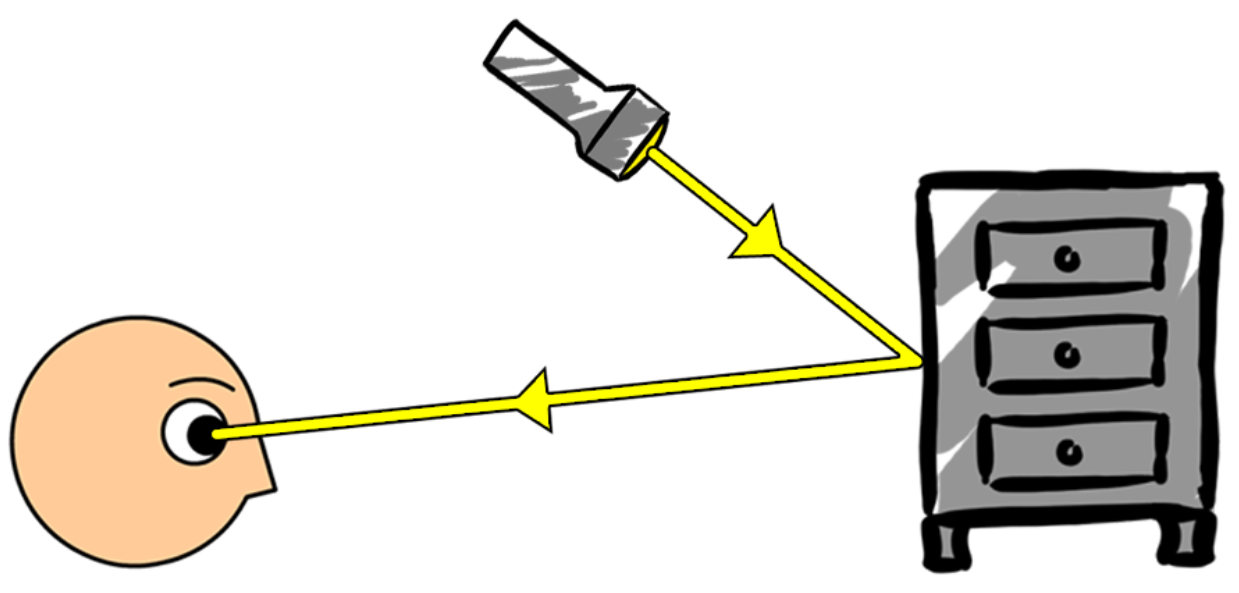
- Er zijn ook voorwerpen die we wel kunnen zien, maar die zelf geen licht geven. Deze voorwerpen kunnen we alleen zien als licht van een lichtbron op deze voorwerpen reflecteert en daarna in onze ogen schijnt. Als je bijvoorbeeld naar een kast kijkt, dan zie je deze kast dankzij reflectie van licht (zie de onderstaande afbeelding). De maan zien we ook op deze manier. De maan geeft zelf geen licht, maar reflecteert het licht van de zon.
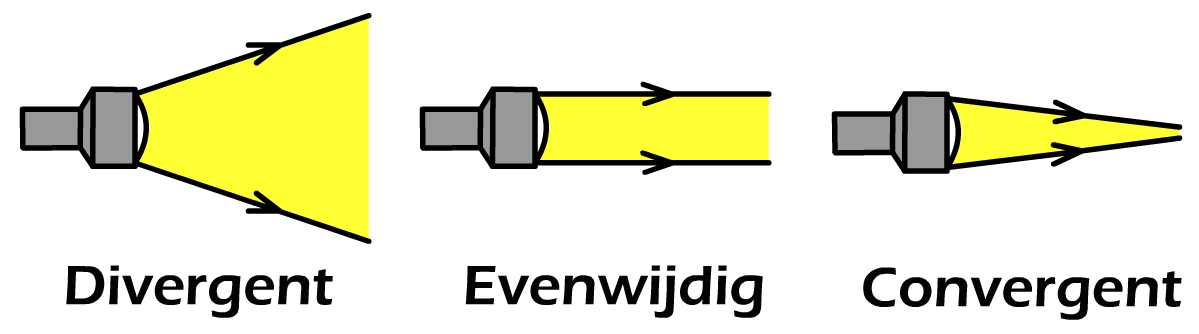
Een collectie van lichtstralen wordt een lichtbundel genoemd. Er zijn drie soorten lichtbundels:
- De evenwijdige lichtbundel is een bundel waarbij alle lichtstralen in dezelfde richting schijnen. Een voorbeeld is de lichtbundel van een laser.
- De divergente lichtbundel is een bundel waarbij de lichtstralen uit elkaar bewegen. Een voorbeeld is de lichtbundel van een zaklamp.
- De convergente lichtbundel is een bundel waarbij de lichtstralen steeds dichter naar elkaar toe gaan. We kunnen dit type lichtbundel bijvoorbeeld produceren met een vergrootglas.
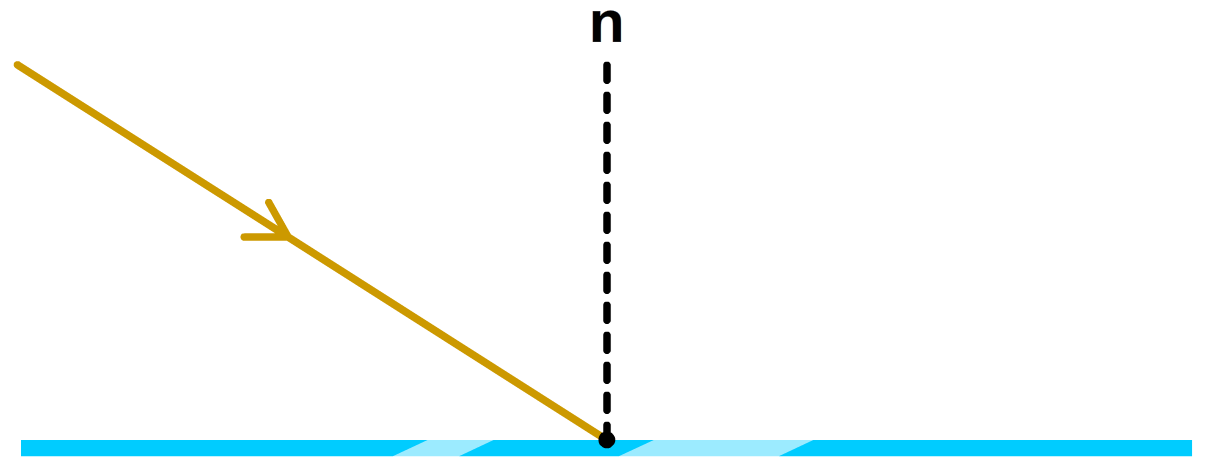
Hieronder zien we een schematische afbeelding van een lichtstraal die op een spiegel valt. Op de plek waar de lichtstraal de spiegel raakt, hebben we een stippellijn getekend. Deze hulplijn wordt de normaal (n) genoemd en staat altijd loodrecht op de spiegel. We kunnen deze hulplijn gebruiken om uit te vinden hoe de lichtstraal zal reflecteren.
In de onderstaande linker afbeelding meten we de hoek tussen de normaal en de invallende lichtstraal. Dit wordt de hoek van inval (i) genoemd. Zorg dat het nulpunt van de geodriehoek precies op het punt ligt waar de lichtstraal invalt en meet dan de hoek. Zorg dat je op de gradenboog van de geodriehoek de hoek afleest die kleiner is dan 90°. In dit voorbeeld lezen we dat de hoek 59 graden is (zie de linker onderstaande afbeelding). Dan draaien we de geodriehoek en tekenen we de gereflecteerde lichtstraal onder dezelfde hoek (weer 59 graden). Dit wordt de hoek van terugkaatsing (t) genoemd (zie de rechter afbeelding).
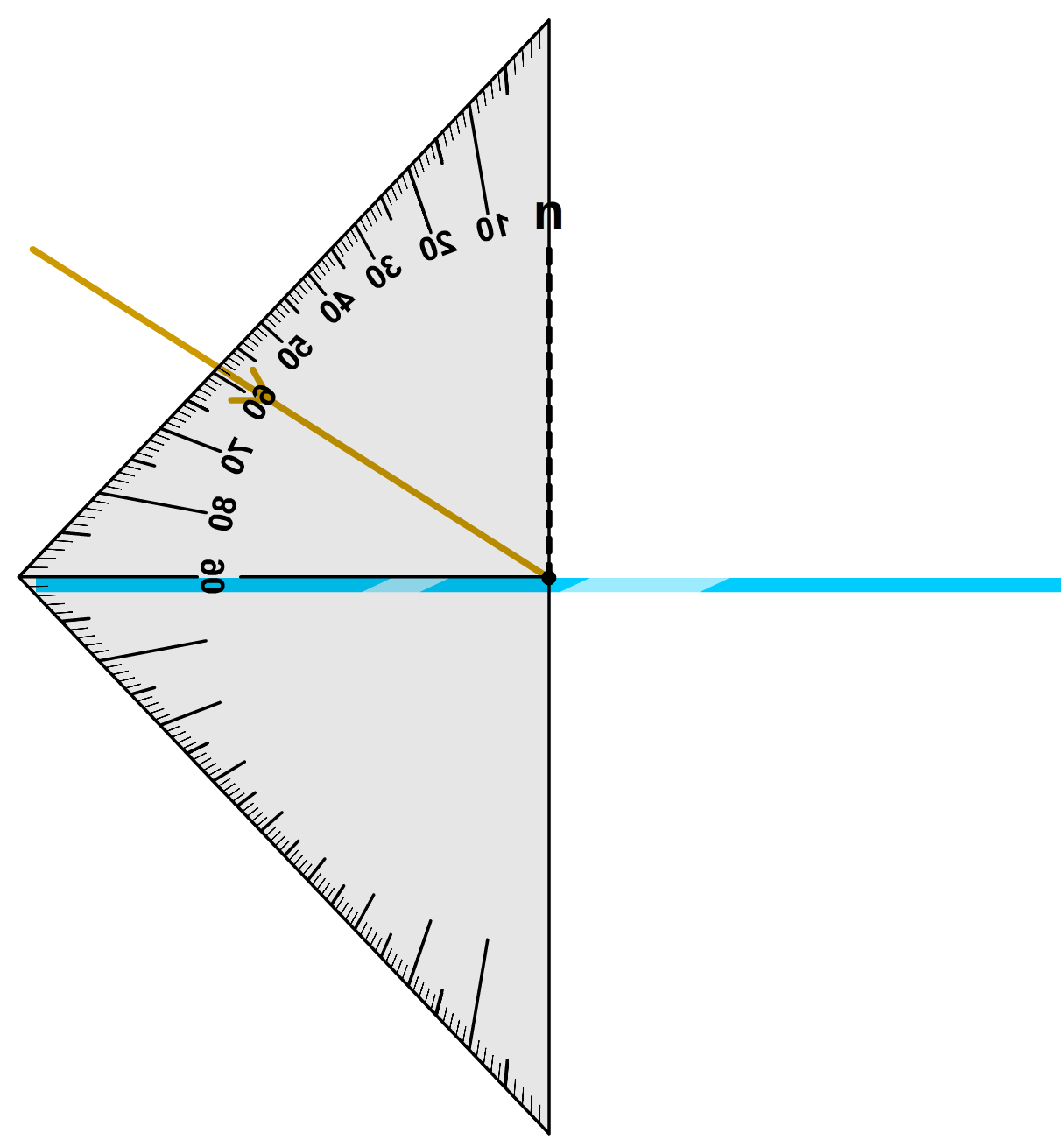
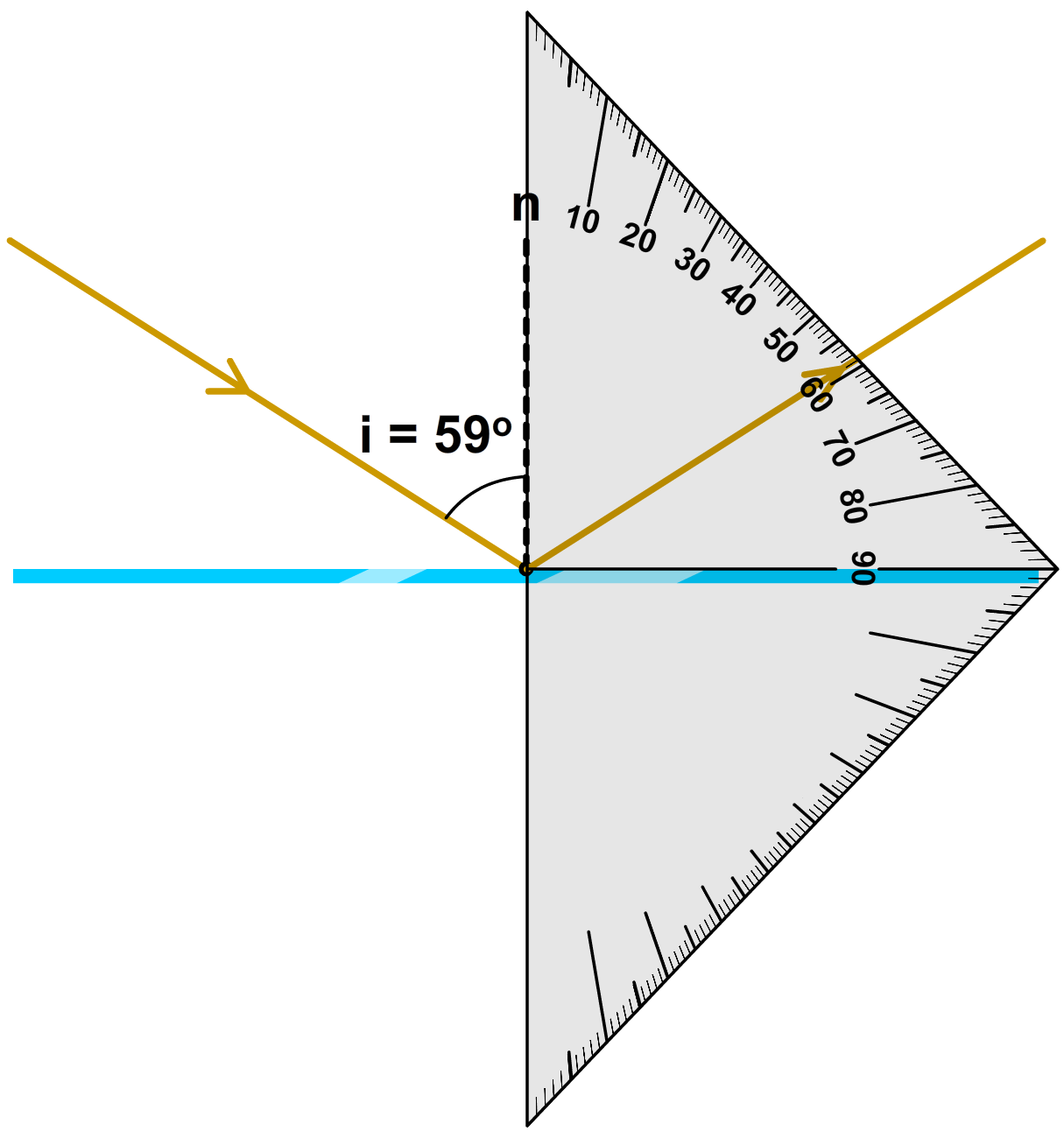
Hieronder zien we het resultaat. Zorg dat je de hoek van inval en de hoek van terugkaatsing netjes in de tekening weergeeft.
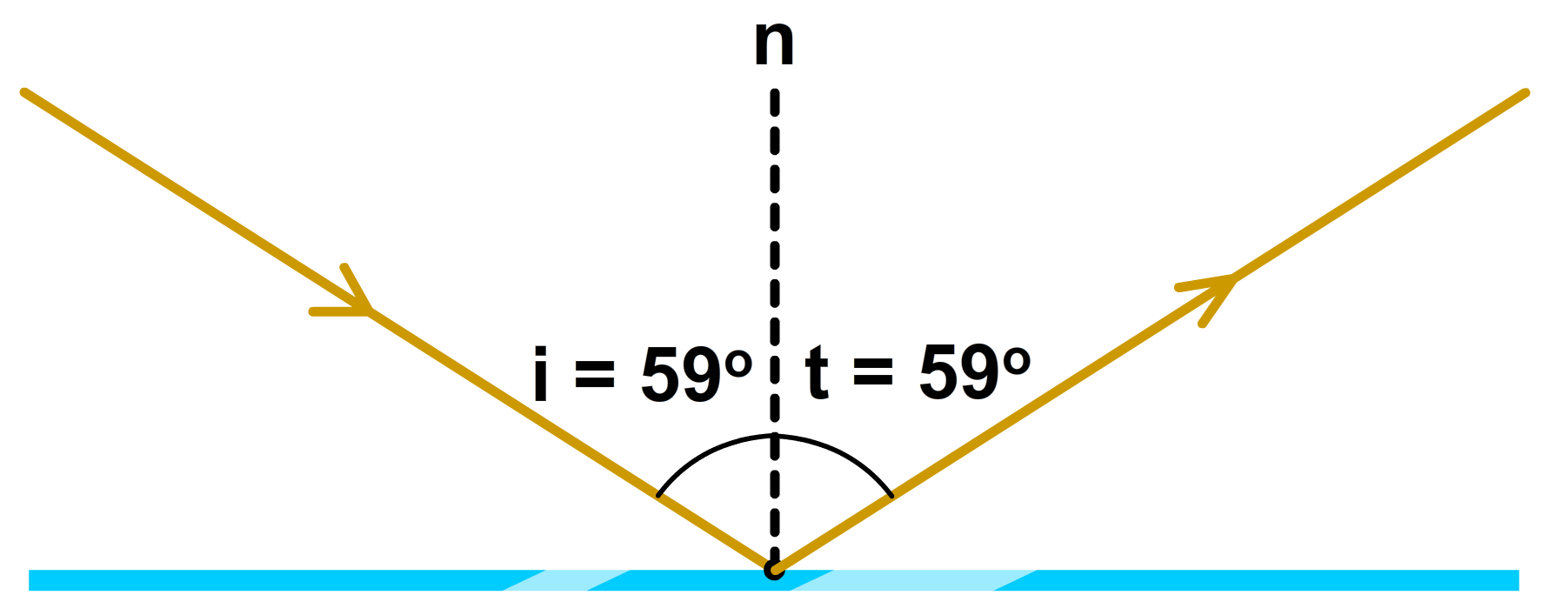
Omdat beide hoeken dus even groot zijn, vatten we de regel voor het tekenen van reflecties als volgt samen:
| $$ \angle i = \angle t $$ |
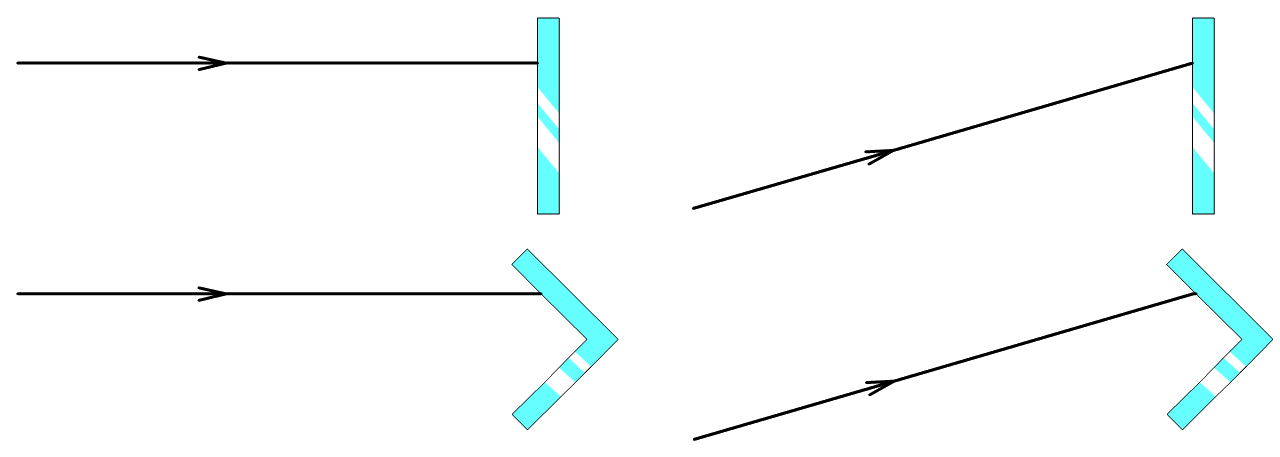
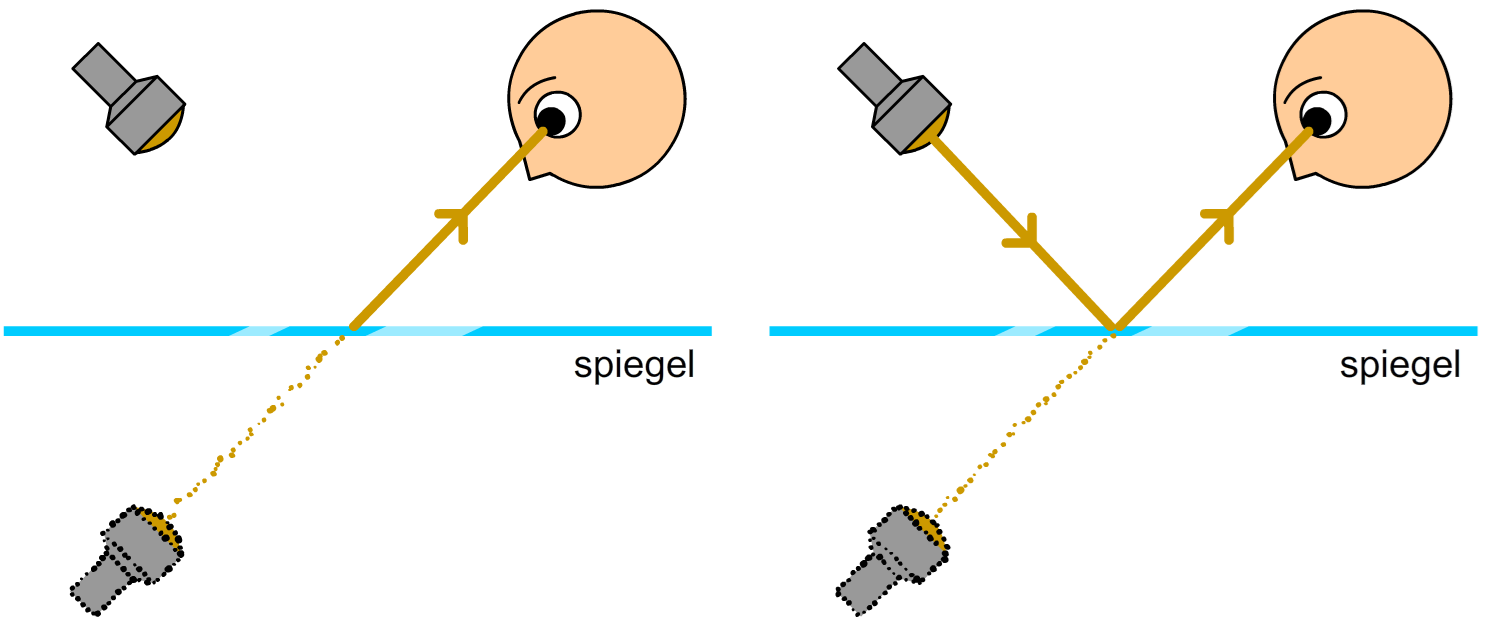
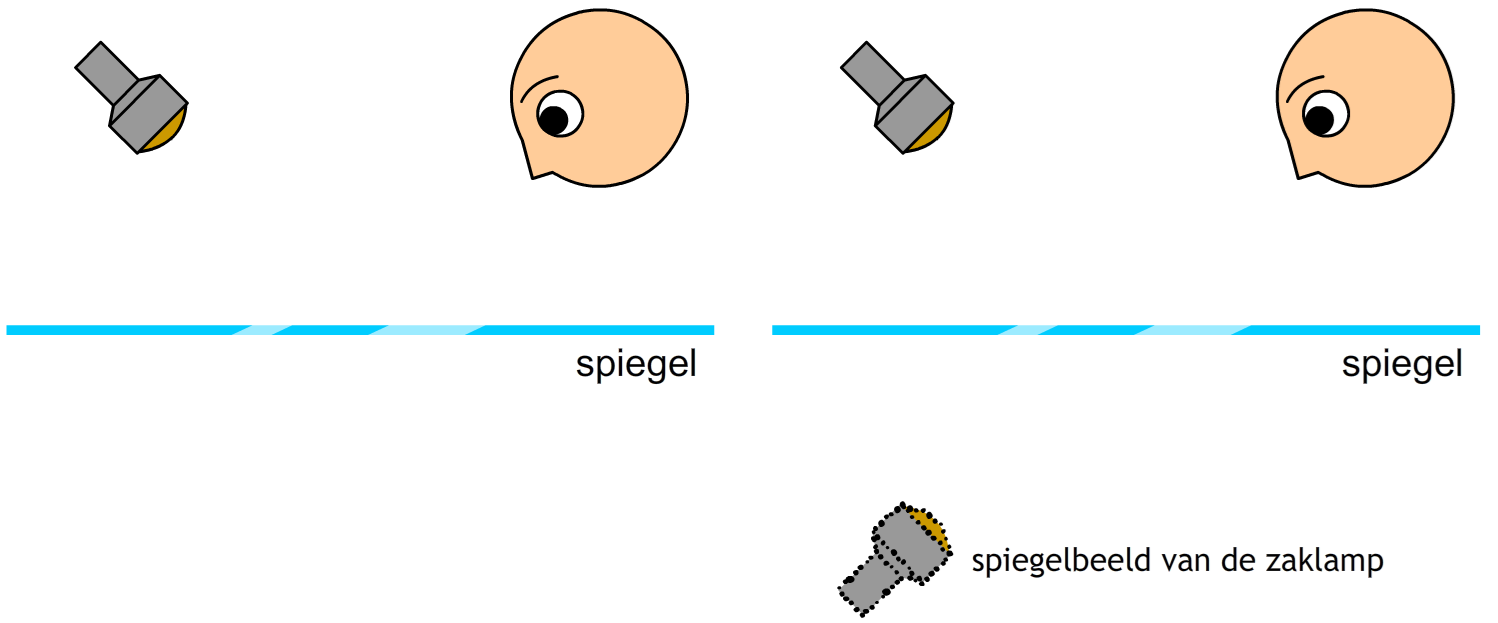
Zoals je weet zorgen spiegels voor een spiegelbeeld. Ook hiermee kunnen we reflecties tekenen. In de linker onderstaande afbeelding zijn we op zoek naar een lichtstraal die vanaf een zaklamp via een spiegel in het oog van de persoon terecht komt. We tekenen hiervoor eerst het spiegelbeeld van de zaklamp aan de andere kant van de spiegel (zie de tweede afbeelding). Voor de persoon lijkt het alsof het licht uit het spiegelbeeld van de zaklamp komt (zie de derde afbeelding). In het echt komt het licht natuurlijk uit de echte zaklamp. Dit hebben we getekend in de laatste afbeelding. We hebben nu de correcte reflectie getekend.
Niet alle voorwerpen reflecteren net zo netjes als een spiegel. Neem bijvoorbeeld een stuk papier. Papier lijkt voor ons oog erg glad, maar als we papier door een microscoop bekijken, dan zien we dat papier helemaal niet zo glad is (zie de onderstaande foto).
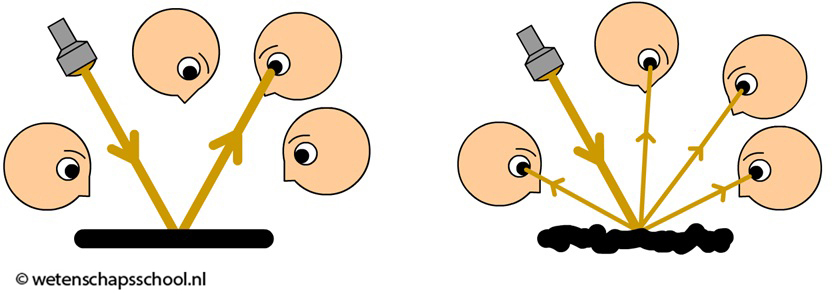
Door het ruwe oppervlak reflecteren lichtstralen alle richtingen op. We noemen dit diffuse reflectie. In de onderstaande afbeelding zien we links reflectie op een spiegel. In dit geval wordt de lichtstraal maar één kant op gereflecteerd. Alleen de persoon die deze lichtstraal in zijn ogen krijgt, kan het licht zien. De rest niet. Rechts zien we diffuse reflectie. Doordat het licht nu alle kanten op gaat, kunnen nu alle omstanders het licht zien, maar het licht is nu wel minder fel.
Leerdoelen:
|
|
|
Opdrachten
|
|
§2 Breking
Als licht van de ene naar de andere stof beweegt, dan verandert het van richting. We noemen dit breking. In deze paragraaf gaan we leren gebroken lichtstralen te tekenen.
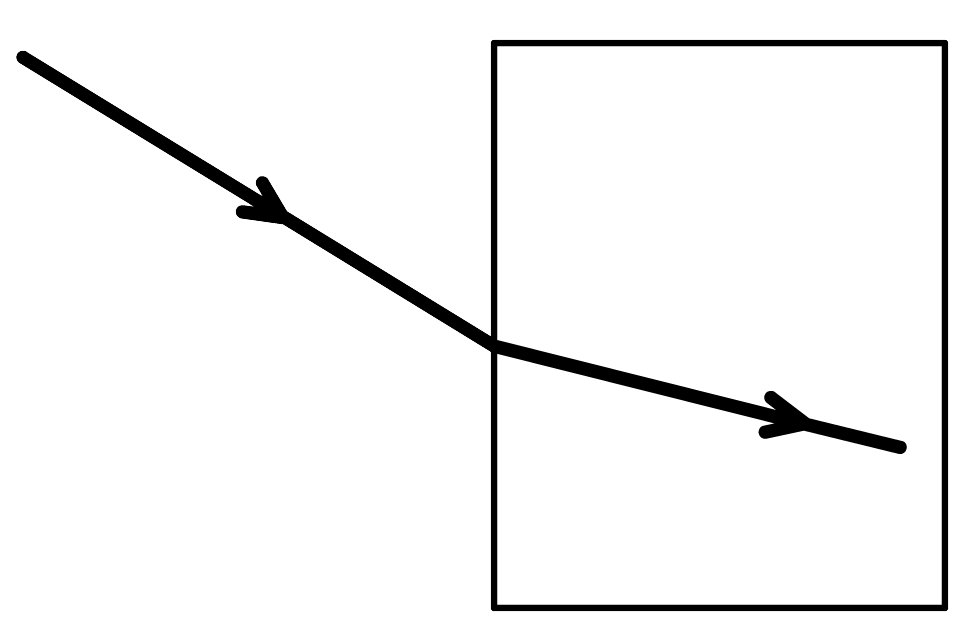
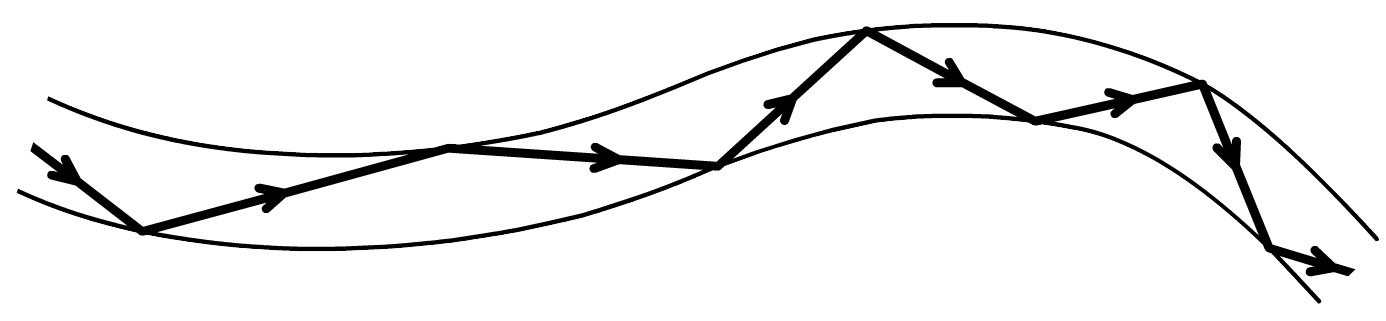
Als licht van de ene naar de andere stof beweegt, dan blijft het licht niet gewoon in een rechte lijn doorbewegen. Op het punt dat het licht overgaat naar een ander materiaal, verandert het van richting. We noemen dit effect breking. In de onderstaande foto is dit effect te zien. Een lichtbundel schijnt een stukje plastic in en daarna weer uit. Merk op dat het licht alleen op de overgangen van de ene naar de andere stof van richting verandert. Op de andere plekken beweegt het licht gewoon in een rechte lijn.
(Afbeelding: ajizai; PD)
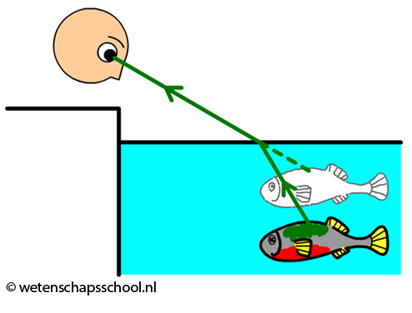
Breking is duidelijk te zien als we naar voorwerpen kijken die zich onder water bevinden. Hieronder is een persoon afgebeeld die naar een vis kijkt. We zien een lichtstraal die vanaf de vis in het oog van een persoon valt. Doordat het licht van richting verandert op het punt dat het licht het water verlaat, lijkt het voor de persoon alsof de vis zich op een andere plek bevindt dan in werkelijkheid het geval is. Zoals je ziet lijkt de vis zich dichter bij het wateroppervlak te bevinden dan in werkelijkheid het geval is.
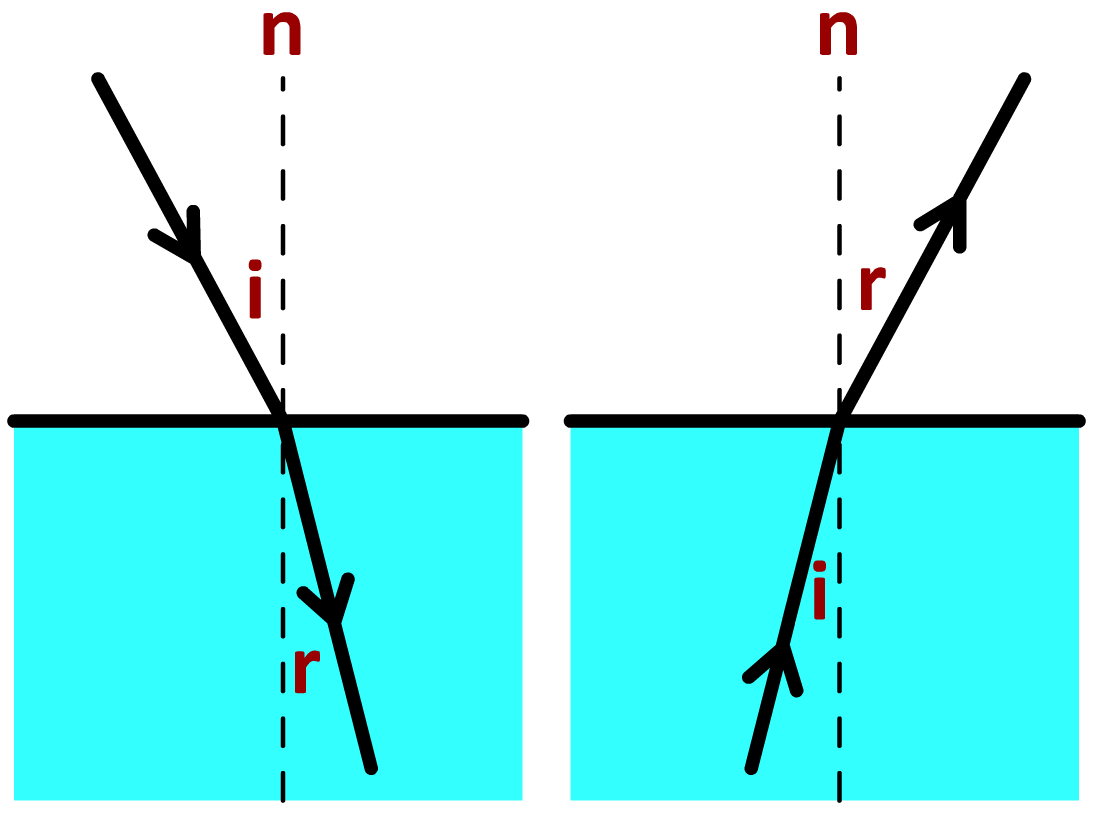
Laten we nu uitrekenen onder welke hoek lichtstralen breken. Zoals je in de onderstaande afbeelding kunt zien, tekenen we de normaal (n) op het punt waar de lichtstraal invalt op het materiaal. De normaal tekenen we in dit geval aan beide kanten van het oppervlak. De hoek tussen de invallende lichtstraal en de normaal noemen we wederom de hoek van inval (i). De hoek tussen de normaal en de gebroken lichtstraal noemen we de brekingshoek (r).
De relatie tussen i en r wordt beschreven met de zogenaamde wet van Snellius:
$$ \frac{\sin{i}}{\sin{r}} = \frac{n_r}{n_i} $$
|
De brekingsindex (n) is een materiaaleigenschap die invloed heeft op de breking. De brekingsindex voor verschillende materialen kan je vinden in BINAS. Voor lucht en het vacuüm geldt een brekingsindex van 1,00. ni staat voor de brekingsindex van het materiaal aan de kant van de invalshoek. nr staat voor de brekingsindex van het materiaal aan de kant van de brekingshoek.
|
Voorbeeld
|
|
Opdracht: Een lichtstraal raakt een wateroppervlak onder een invalshoek van 20°. Bereken de brekingshoek. Antwoord: Volgens BINAS is de brekingsindex van lucht 1,0 en van water 1,3. De formule wordt hiermee: $$ \frac{\sin{20^\circ}}{\sin{r}} = \frac{1,3}{1} $$Dit kunnen we omschrijven tot: $$ \sin{r} = \frac{\sin{20^\circ}}{1,3} $$Met de inverse sinus vinden we dan: $$ r = \sin^{-1}{\left( \frac{\sin{20^\circ}}{1,3} \right) } = 15^\circ $$Zoals je kan zien is de brekingshoek in dit geval kleiner dan de hoek van inval. Dit blijkt altijd het geval te zijn als licht beweegt naar een stof met een hogere brekingsindex.
|
|
Voorbeeld
|
|
Opdracht: Een lichtstraal begint onder water en raakt het wateroppervlak onder een invalshoek van 20°. Bereken de brekingshoek waaronder de lichtstraal de lucht in schijnt. Antwoord: Volgens BINAS is de brekingsindex van lucht 1,0 en van water 1,3. De formule wordt hiermee: $$ \frac{\sin{20^\circ}}{\sin{r}} = \frac{1}{1,3} $$Dit kunnen we omschrijven tot: $$ \sin{r} = \sin{20^\circ} \times 1,3 $$Met de inverse sinus vinden we dan: $$ r = \sin^{-1}{\left( \sin{20^\circ} \times 1,3 \right) } = 26^\circ $$Zoals je kan zien is de brekingshoek in dit geval groter dan de hoek van inval. Dit blijkt altijd het geval te zijn als licht beweegt naar een stof met een lagere brekingsindex.
|
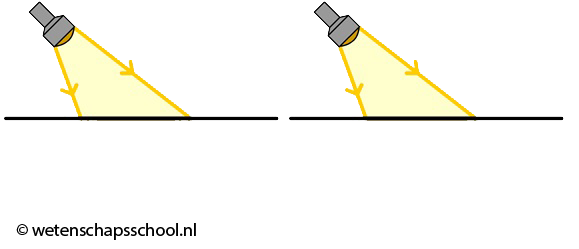
Het resultaat van het bovenstaande voorbeeld levert in sommige gevallen problemen op. Als we de hoek van inval steeds groter maken, dan komt er een moment dat de brekingshoek groter zou moeten worden dan 90° (zie de onderstaande afbeelding). Als je de wet van Snellius in deze gevallen probeert op te lossen, dan geeft de rekenmachine een error. In dat geval vindt er geen breking plaats. Wat er in plaats hiervan gebeurt, is dat de lichtstraal reflecteert. We spreken hier ook wel van totale reflectie (zie de laatste twee zaklampen in de onderstaande afbeelding). Ook bij dit type reflectie geldt ∠i = ∠t.
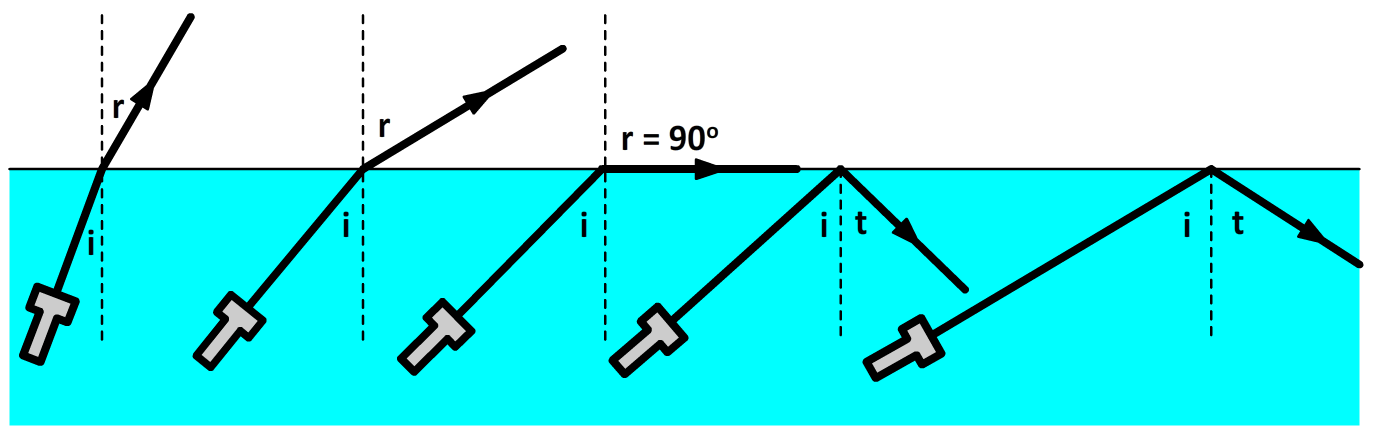
Zoals je in de bovenstaande afbeelding kan zien, vindt er breking plaats tot de brekingshoek 90 graden is. De specifieke hoek van inval waarbij dit gebeurt noemen we de grenshoek (g). Deze hoek kunnen we vinden met de wet van Snellius:
$$ \frac{\sin{i}}{\sin{r}} = \frac{n_r}{n_i} $$Voor de brekingshoek (r) vullen we nu 90 graden in en voor de invalshoek i vullen we de grenshoek (g) in:
$$ \frac{\sin{g}}{\sin{90^\circ}} = \frac{n_r}{n_i} $$Omdat sin(90°) = 1, kunnen we dit herschrijven tot:
$$ \sin{g} = \frac{n_r}{n_i} $$
|
Deze formule kan je gebruiken om de grenshoek te vinden.
In het onderstaande programma is het moment te zien waarop totale reflectie plaatsvindt. Klik met je muis om te lichtstraal te richten. Als je op de knop "gedeeltelijke reflectie" klikt, dan zie je dat ook voordat de grenshoek bereikt is al deels reflectie optreedt. In dit hoofdstuk is het niet nodig hier rekening mee te houden.
|
Leerdoelen:
|
|
|
Opdrachten
|
|
§3 Het beeld
In deze paragraaf gaan we beginnen met het bestuderen van lenzen. Een lens werkt met behulp van breking en hiermee kunnen we een beeld van de werkelijkheid projecteren op een scherm. In deze paragraaf gaan we leren hoe dit werkt.
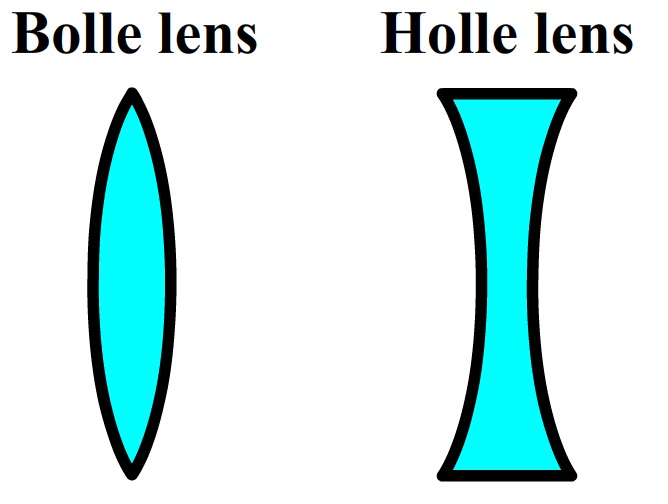
Lenzen komen we in het dagelijks leven veel tegen. Ze zitten in brillen, camera's, microscopen, telescopen en ook het oog zelf bevat een lens. Lenzen werken doordat ze licht op een speciale manier breken. Er bestaan twee typen lenzen. Een bolle lens, ook wel een positieve lens genoemd, is in het midden dikker dan aan de rand. Een holle lens, ook wel een negatieve lens genoemd, is in het midden dunner dan aan de rand (zie de onderstaande rechter afbeelding). Als een evenwijdige bundel op een bolle lens valt, dan convergeert de bundel naar één punt. Dit zien we bijvoorbeeld bij een vergrootglas (zie de onderstaande linker afbeelding). Bij de holle lens convergeren de lichtstralen juist weg van één punt.
(Afbeelding: Landon; CC BY-ND 2.0)
Positieve lenzen tekenen we meestal als een verticale lijn met daarboven een plus. Een negatieve lens tekenen we als een verticale lijn met daarboven een min. Ook tekenen we door het midden van de lens een horizontale lijn. Dit is een hulplijn die we de hoofdas noemen.
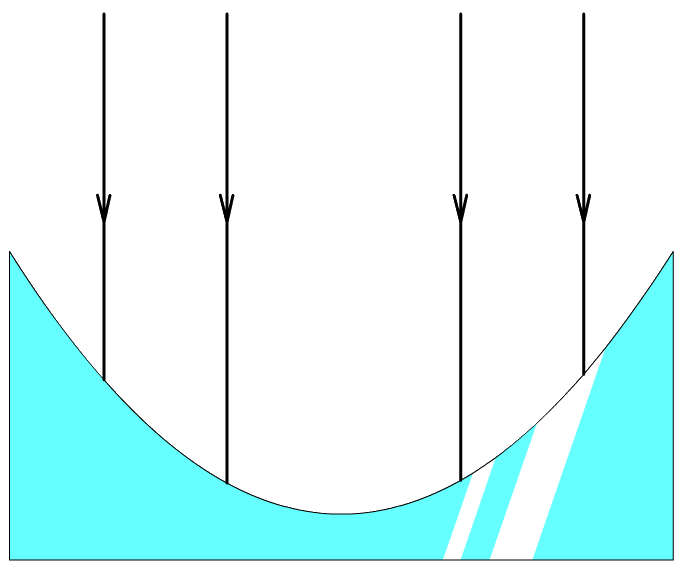
Als lichtstralen evenwijdig aan de hoofdas op een positieve lens vallen, dan kruisen ze elkaar in een punt op de hoofdas dat we het brandpunt noemen (zie de onderstaande linker afbeelding). Het brandpunt duiden we aan met de letter F (van het Engelse woord "focus"). Let op dat alleen deze evenwijdige lichtstralen in het brandpunt terecht komen. Alle andere lichtstralen komen nooit in het brandpunt terecht. Als lichtstralen evenwijdig aan de hoofdas op een negatieve lens vallen, dan bewegen ze juist weg van het brandpunt dat zich aan de andere zijde van de lens bevindt (zie de rechter afbeelding).
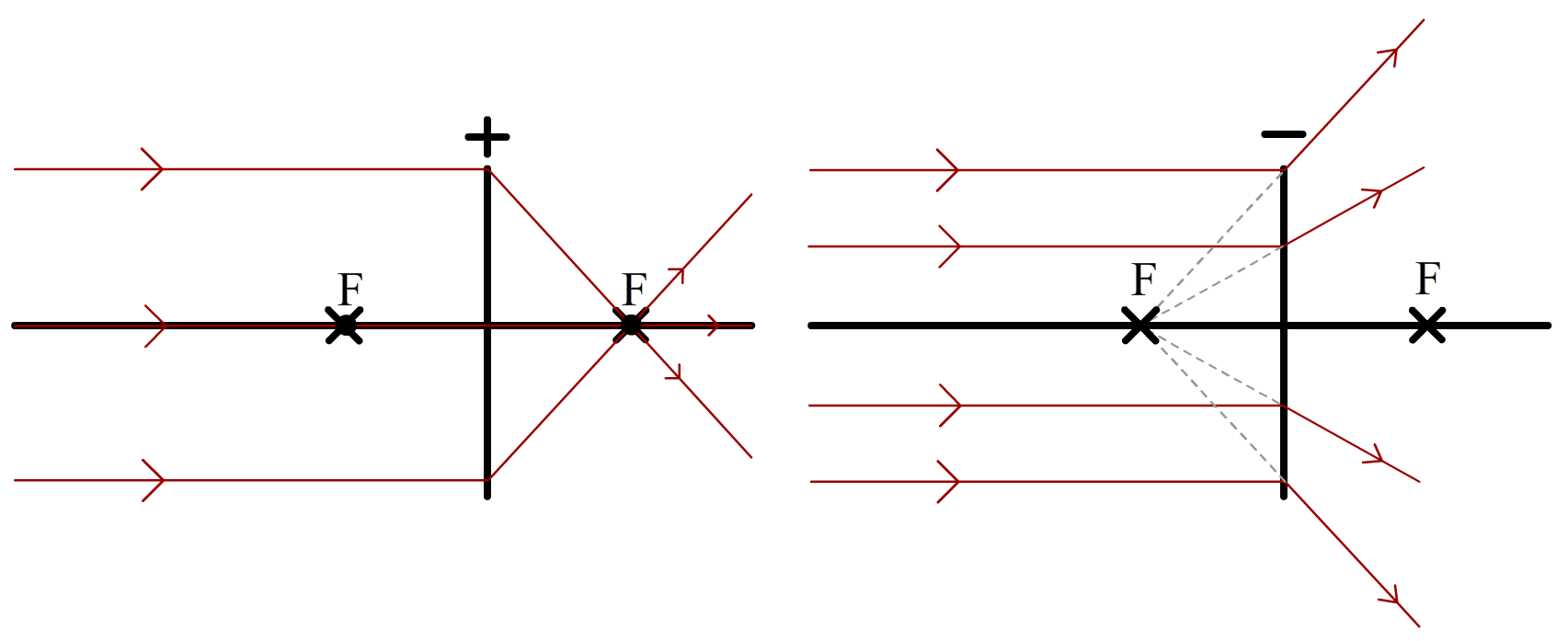
De afstand van het midden van de lens tot het brandpunt wordt de brandpuntsafstand (f) genoemd. Hoe boller (of holler) de lens, hoe kleiner de brandpuntsafstand.
Opticiens gebruiken in plaats van de brandpuntsafstand (f) liever de lenssterkte (S). De lenssterkte wordt gemeten in dioptrie (dpt). In de bovenstaande foto zien we bijvoorbeeld een bril met een lenssterkte van +2,50 dpt. We kunnen de lenssterkte als volgt uitrekenen:
$$ S = \frac{1}{f} $$
|
Let op dat je de brandpuntsafstand in deze formule altijd in meters invult.
In de onderstaande foto zien we dat er met een lens aan de linkerzijde een beeld is gemaakt van een kaarsje. Zoals je kan zien staat dit beeld "op z'n kop". In de rest van deze paragraaf gaan we begrijpen wat er hier gebeurt.
In de onderstaande afbeelding is links een lampje weergegeven. Dit lampje straalt licht uit in alle richtingen. Slechts een deel van deze lichtstralen komt op de lens terecht.
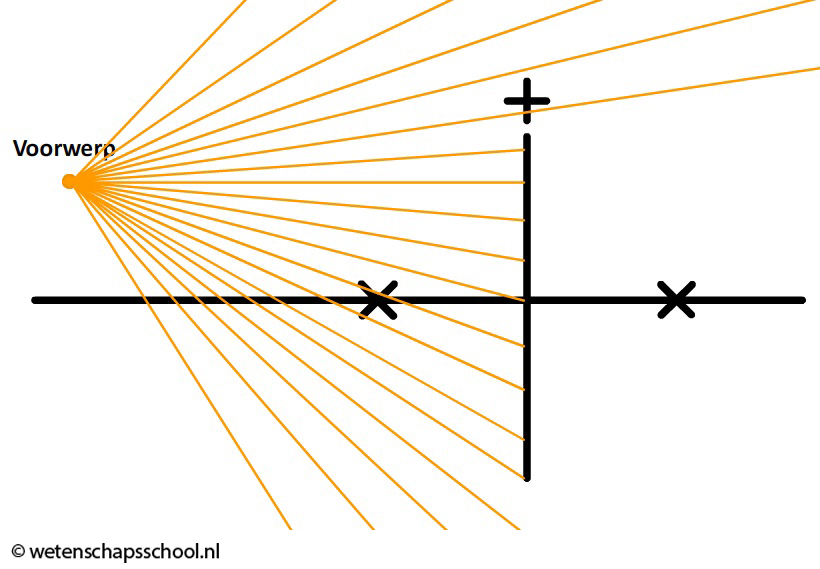
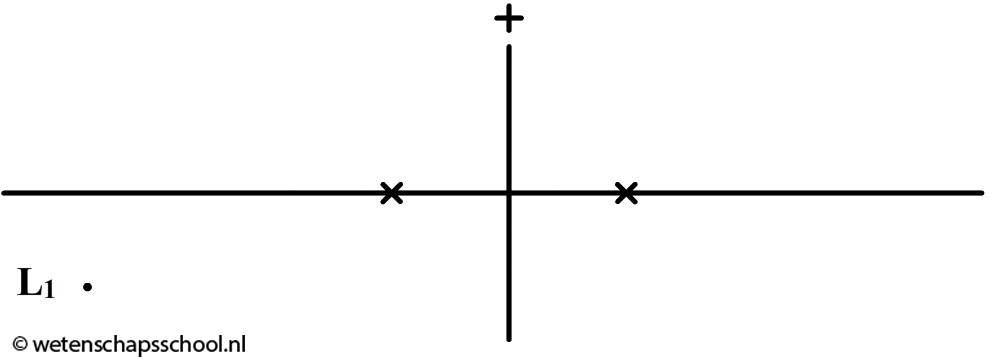
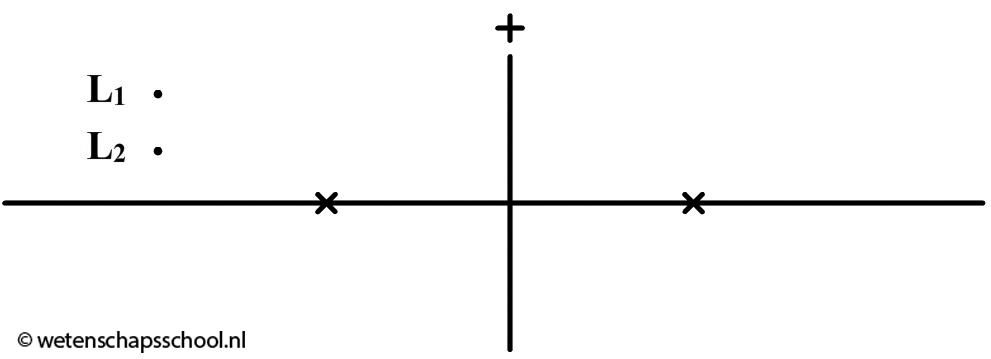
Van al de lichtstralen die op de lens vallen, gaan we er slechts twee bestuderen (zie de onderstaande linker afbeelding). We noemen dit je constructiestralen. De bovenste lichtstraal loopt evenwijdig aan de hoofdas. We weten dus dat deze lichtstraal door het brandpunt gaat. De onderste lichtstraal gaat door het midden van de lens. Lichtstralen door het midden van de lens gaan gewoon rechtdoor.
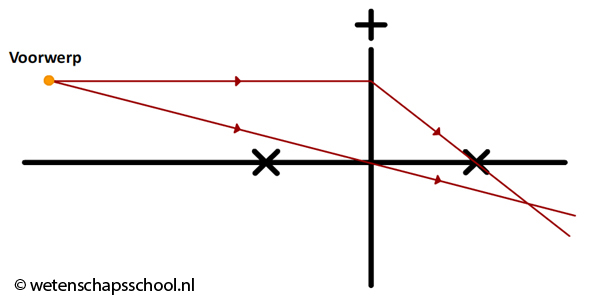
Nu plaatsen we een scherm. Als we het scherm precies op de plek plaatsen deze lichtstralen samenkomen, dan krijgen we een scherp beeld van dit lampje te zien op dit scherm.
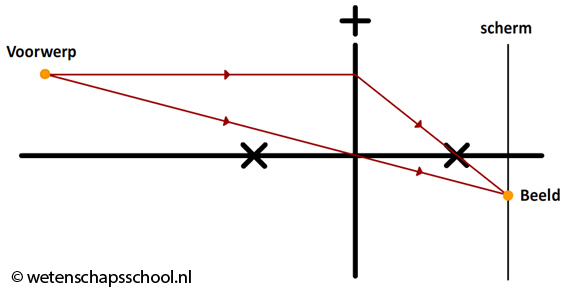
Nu kunnen we ook andere lichtstralen tekenen die op de lens terecht komen. Ook deze lichtstralen komen namelijk samen op hetzelfde punt op het scherm. Merk op dat de plek waar de lichtstralen samenkomen niet het brandpunt is. Dit is logisch, want niet alle lichtstralen lopen evenwijdig aan de hoofdas.
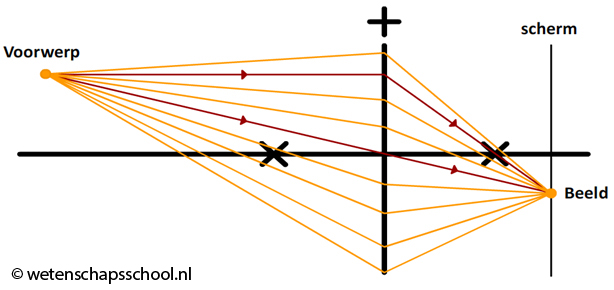
Nu gaan we een beeld maken van een voorwerp, in dit geval van een pijltje. In de onderstaande afbeelding hebben we de twee constructiestralen getekend die uit het puntje van de pijl komen.
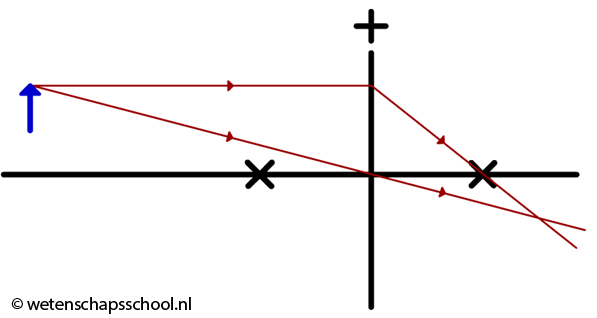
In de onderstaande afbeelding zien we ook de constructiestralen die van de onderkant van de pijl komen. In deze afbeelding is ook een scherm geplaatst op de plekken waar de lichtstralen samenkomen.
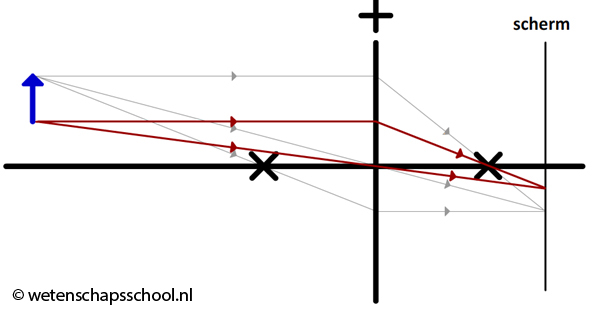
Merk op dat het licht afkomstig van het puntje van de pijl lager op het scherm terecht komt dan het licht van de onderkant van de pijl. Het beeld van de pijl staat dus inderdaad "op z'n kop". In de onderstaande afbeelding hebben we het beeld getekend dat op het scherm zichtbaar zal zijn.
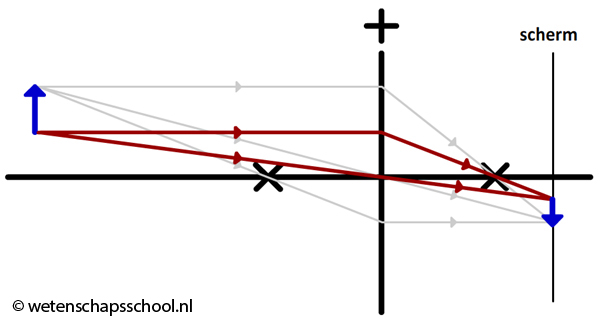
In het onderstaande programma kan je de pijl verplaatsen. Rechts is dan het bijbehorende beeld te zien. Als je het object voorbij het brandpunt trekt gebeurt er wel wat vreemds, maar dat is onderwerp van de volgende paragraaf.
|
Leerdoelen:
|
|
|
Opdrachten
|
|
§4 Het virtuele beeld
Als we een voorwerp dichter bij de lens plaatsen dan het brandpunt, dan ontstaat een zogenaamd virtueel beeld. In deze paragraaf gaan we bestuderen wat dit is.
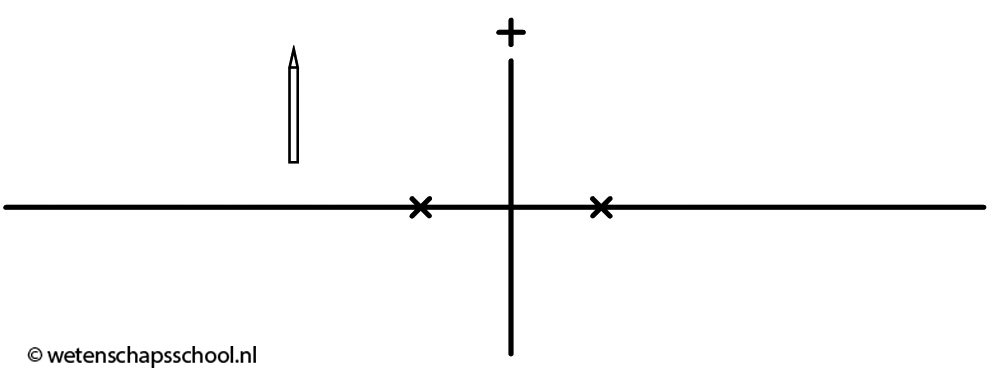
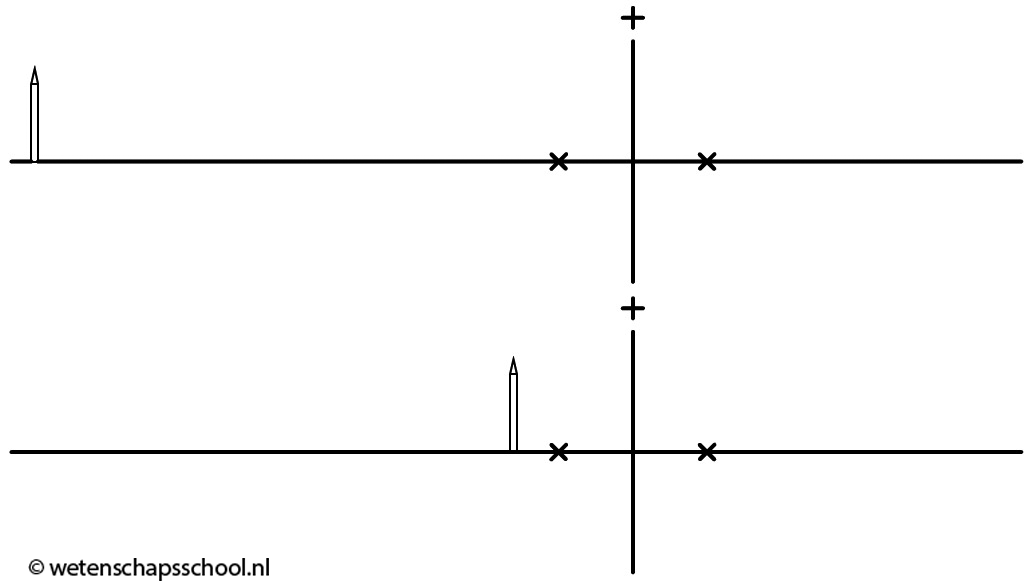
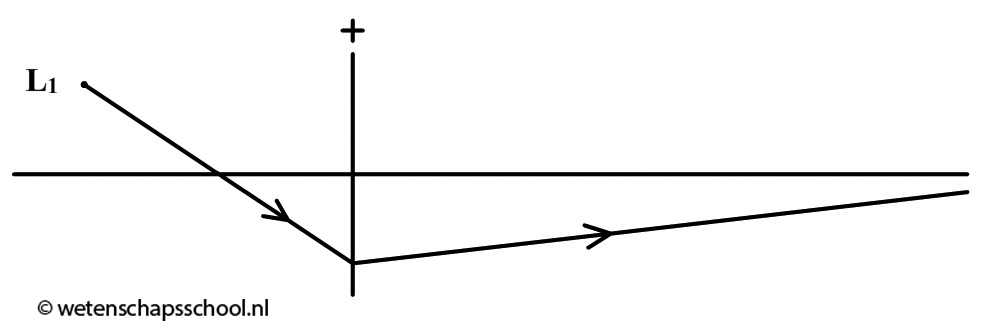
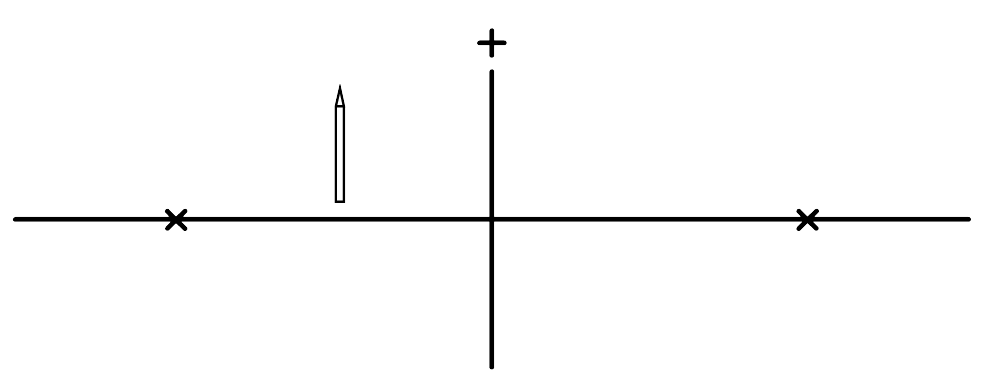
Als we het voorwerp dichter bij de lens plaatsen dan het brandpunt, dan kunnen we op de gebruikelijke manier de constructiestralen tekenen. De lichtstraal door het midden gaat rechtdoor. De lichtstraal evenwijdig aan de hoofdas gaat door het rechter brandpunt. Probleem is echter dat de lichtstralen nu nergens samenkomen (zie de onderstaande afbeelding). We kunnen dus nergens een scherm plaatsen waarop het beeld geprojecteerd wordt. We kunnen wel het volgende doen. Als we de lichtstralen opvangen met bijvoorbeeld ons oog, dan lijkt het of de lichtstralen uit een ander punt komen dan in werkelijkheid het geval is. We spreken hier van een virtueel beeld (in tegenstelling tot een reëel beeld). Dit beeld wordt virtueel genoemd, omdat er niet werkelijk licht op dit beeld samenkomt. Het licht lijkt er alleen vandaan te komen.
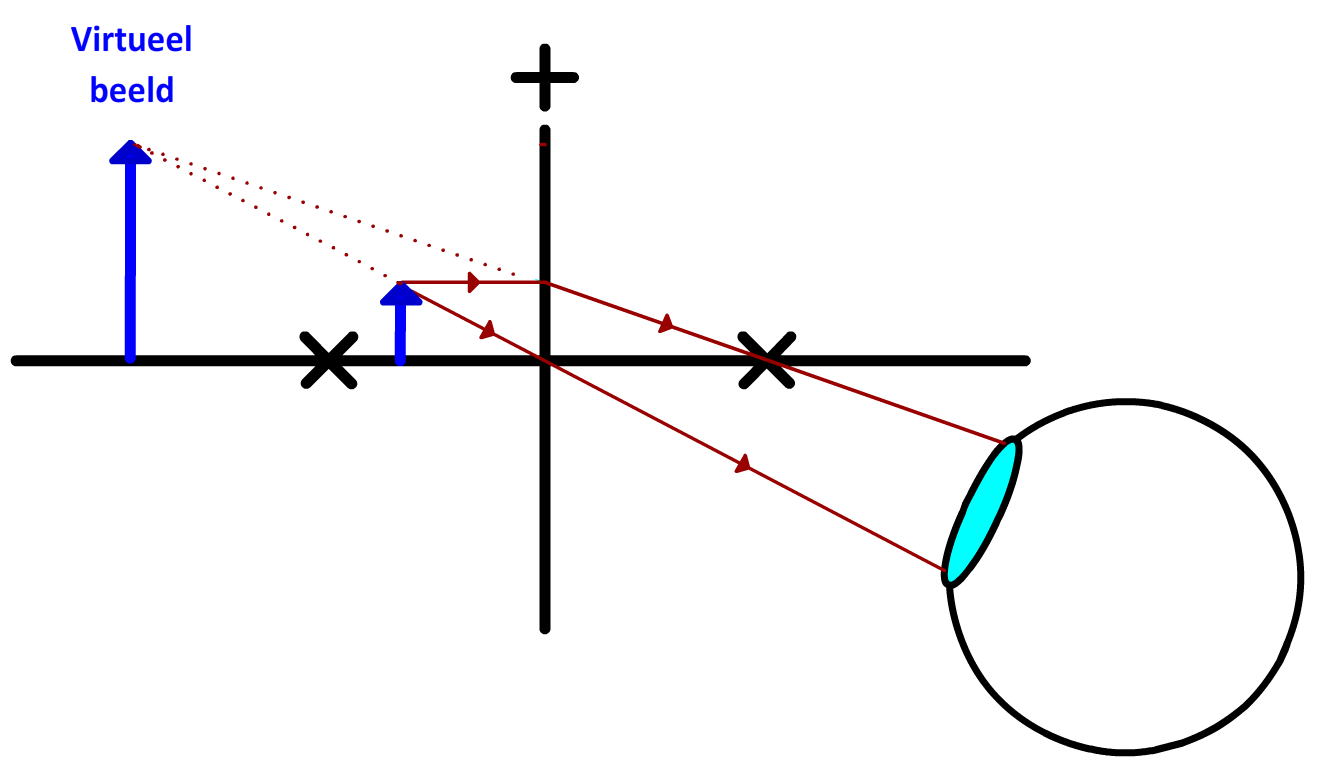
Merk ook op dat het virtuele beeld aan dezelfde kant staat als het voorwerp en dat het virtuele beeld niet "op z'n kop" staat.
Met het onderstaande programma kan je zowel een reëel als een virtueel beeld maken. Sleep hiervoor het object heen en weer.
|
Leerdoelen:
|
|
|
Opdrachten
|
|
§5 De lenzenformule
In deze paragraaf gaan we leren rekenen met de lenzenformule.
In de onderstaande afbeelding is links een voorwerp getekend (een blauwe pijl) en rechts zien we het beeld van dit voorwerp afgebeeld op een scherm. De afstand van de lens tot het voorwerp noemen we de voorwerpafstand (v) en de afstand van de lens tot het beeld noemen we de beeldafstand (b). De hoogte van het voorwerp noemen we V en de hoogte van het beeld noemen we B.
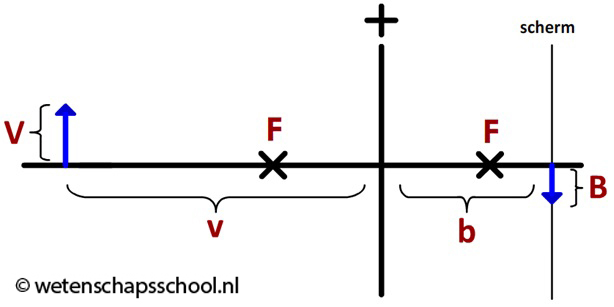
Met deze afstanden kunnen we de vergroting (N) berekenen. Dit kunnen we doen met de volgende twee formules:
$$ N = \frac{B}{V} $$
$$ N = \frac{b}{v} $$
|
Als de vergroting (N) bijvoorbeeld gelijk is aan 2, dan is het beeld twee keer zo groot als het voorwerp. Als N = 0,5 dan is het beeld twee keer zo klein als het voorwerp. De formule werkt ook als de afstanden in andere eenheden gegeven worden, bijvoorbeeld in centimeters.
Met de voorwerpsafstand en de beeldafstand kunnen we ook de brandpuntsafstand (f) berekenen. We doen dit met de zogenaamde lenzenformule:
$$ \frac{1}{f} = \frac{1}{b} + \frac{1}{v} $$
|
|
Voorbeeld
|
|
Opdracht: Een persoon wilt een scherpe foto maken van een potlood. De voorwerpsafstand is 50,0 cm en de beeldafstand is 5,0 cm. Bereken de brandpuntsafstand van de lens die je nodig hebt. Antwoord: Eerst vullen we de formule in en rekenen we de rechter zijde uit: $$ \frac{1}{f} = \frac{1}{5,0} + \frac{1}{50,0} $$ $$ \frac{1}{f} = 0,22 $$Als we deze formule omschrijven, dan vinden we: $$ f = \frac{1}{0,22} = 4,5 \text{ cm} $$De brandpuntsafstand is dus 4,5 cm.
|
|
Voorbeeld
|
|
Opdracht: Met een lens van 30 dpt maken we een beeld van een voorwerp dat zich 8,0 cm van de lens bevindt. Bereken hoe ver je het scherm van de lens moet zetten om een scherp beeld te krijgen. Antwoord: Eerst rekenen we met de lenssterkte de brandpuntsafstand uit: $$ f = \frac{1}{S} $$ $$ f = \frac{1}{30} = 0,03333 \text{ m} $$Let erop dat bij deze formule het antwoord altijd in meter wordt gegeven. Met de brandpuntsafstand kunnen we met de lenzenformule de beeldafstand uitrekenen. Eerst vullen we de formule in: $$ \frac{1}{f} = \frac{1}{b} + \frac{1}{v} $$ $$ \frac{1}{0,03333} = \frac{1}{b} + \frac{1}{0,080} $$ $$ 30 = \frac{1}{b} + 12,5 $$We zien hier dat 1/b gelijk moet zijn aan 30 - 12,5 = 17,5. Er geldt dus: $$ 17,5 = \frac{1}{b} $$Deze formule kunnen we omschrijven en oplossen: $$ b = \frac{1}{17,5} = 0,057 \text{ m} $$De beeldafstand is dus 0,057 m, oftewel 5,7 cm.
|
|
Extra: Rekenen aan een virtueel beeld
|
|
In het geval van een virtueel beeld werkt de lenzenformule ook. Het beeld bevindt zich in dat geval aan de "andere kant" van de lens. Dit zien we terug doordat de beeldafstand in de formule automatisch een negatieve waarde krijgt. Als de afstand van het virtuele beeld tot de lens bijvoorbeeld 10 cm is, dan vullen we in de lenzenformule voor b dus -10 cm in.
|
|
Leerdoelen:
|
|
|
Opdrachten
|
|