Hoofdstuk 3
Radioactiviteit
§1 Kernverval §2 Halveringstijd §3 Activiteit §4 Stralingsgevaar §5 E = mc2 (VWO) §6 Medische beeldvorming
§1 Kernverval
In dit hoofdstuk gaan we begrijpen wat radioactiviteit is. Ook gaan we kijken naar de gevaren en bespreken we hoe radioactiviteit kan worden toegepast als energiebron en hoe het in het ziekenhuis wordt gebruikt om het menselijk lichaam in kaart te brengen. We beginnen in de eerste paragraaf met het bestuderen van kernverval.
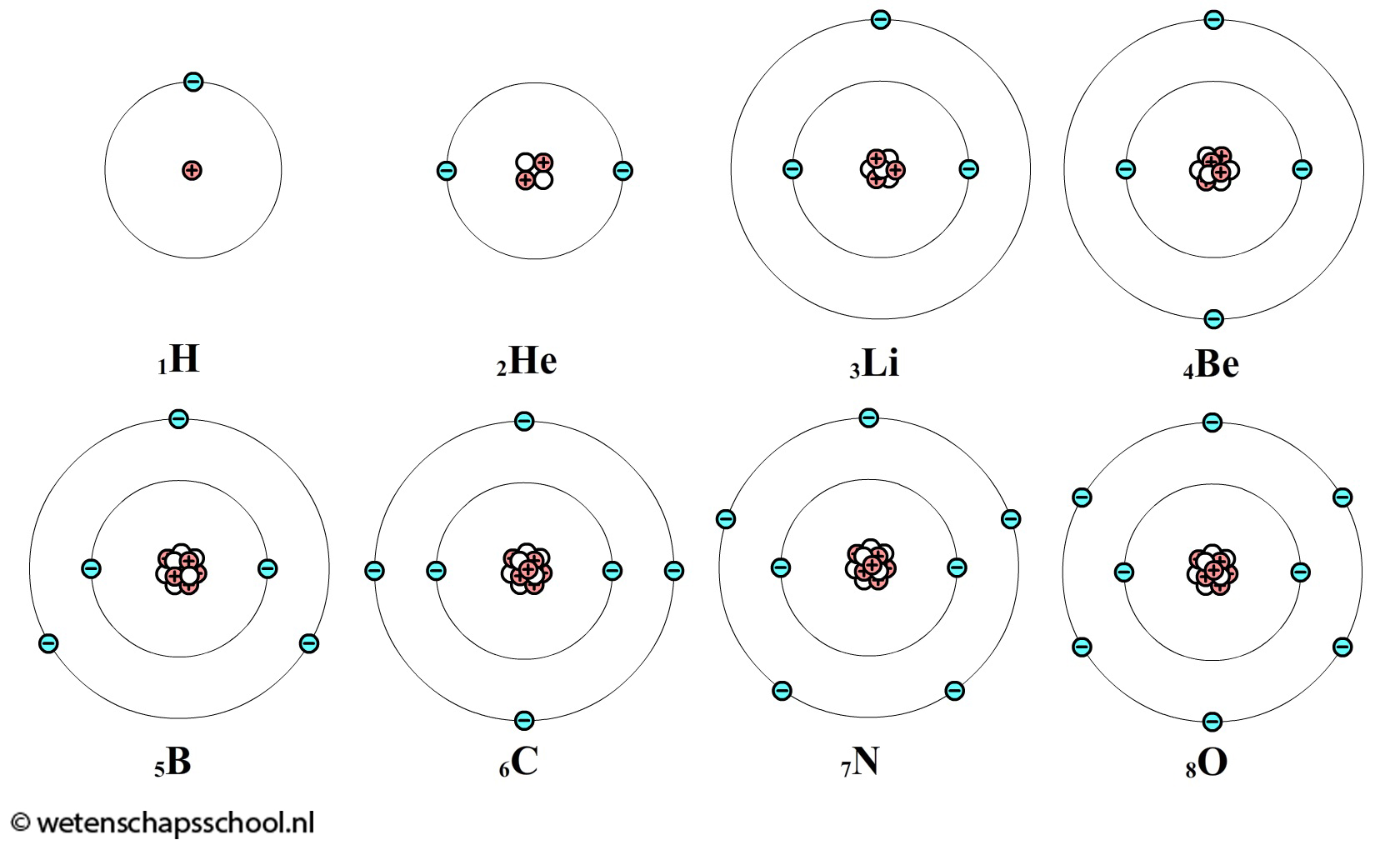
Atomen bestaan uit allerlei kleine deeltjes. Elk atoom heeft in zijn centrum een atoomkern, bestaande uit positief geladen deeltjes die we protonen (p) noemen en neutraal geladen deeltjes die we neutronen (n) noemen. Om de kern heen bevindt zich een wolk van negatieve deeltjes die we elektronen (e) noemen. Een atoom is altijd neutraal en bevat dus evenveel protonen als elektronen. In de onderstaande afbeelding zien we de zes lichtste atomen. Waterstof (H) bestaat uit één proton en dus ook één elektron. Helium (He) bestaat uit twee protonen en dus ook twee elektronen. Lithium (Li) bevat drie protonen en dus ook drie elektronen. Etc. Als het aantal protonen en elektronen niet gelijk is, dan spreken we niet van een atoom, maar van een ion.
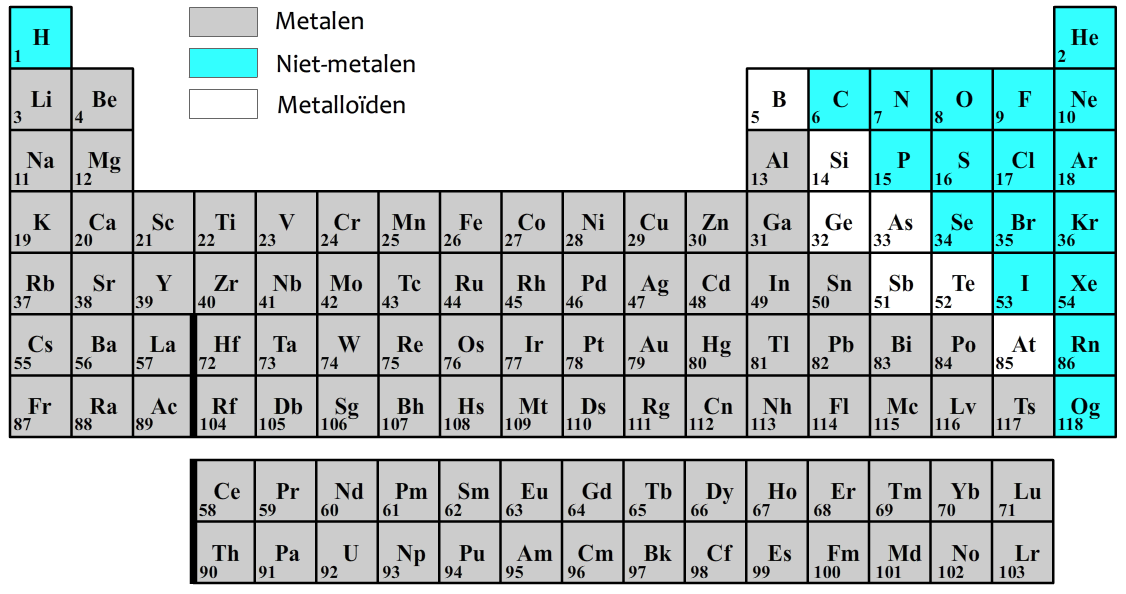
De materie om ons heen bestaat uit 118 soorten atomen. De symbolen behorende bij deze 118 atoomsoorten vinden we in de onderstaande tabel, genaamd het periodiek systeem. Je kan deze tabel ook in BINAS vinden. Linksonder de symbolen kan je voor elk atoom het atoomnummer vinden. Dit komt overeen met het aantal protonen in de kern van het atoom. Het is belangrijk te onthouden dat voor elke atoomsoort het atoomnummer vast staat. IJzer (Fe) heeft bijvoorbeeld altijd atoomnummer 26 (ga dit zelf na!).
Het aantal protonen en neutronen samen noemen we het massagetal. Het massagetal wordt vaak achter de naam van het element genoemd. Fluor-19 heeft dus een massagetal van 19. Omdat fluor volgens het periodiek systeem 9 protonen heeft, moet het dus ook nog 10 neutronen bevatten, zodat het aantal protonen en neutronen samen 9 + 10 = 19 wordt. Waterstof-1 heeft een atoomnummer van 1 en bevat dus slechts 1 proton. Het massagetal van waterstof is ook 1, dus waterstof bevat 0 neutronen (omdat 1 + 0 = 1).
Het massagetal wordt ook geregeld linksboven het symbool van het element genoteerd. Het atoomnummer en massagetal schrijven we dan als volgt op:
$$^{\;\;\;\text{ massagetal}}_{\text{atoomnummer}}\text{Element}$$Het massagetal van een atoomsoort staat niet vast. Zo heb je bijvoorbeeld koolstof-12 en koolstof-14. In het periodiek systeem kunnen we zien dat koolstof altijd 6 protonen in de kern heeft. Om op het juiste massagetal uit te komen moet koolstof-12 nog 6 neutronen in de kern hebben (want 6 + 6 = 12) en moet koolstof-14 nog 8 neutronen in de kern hebben (want 6 + 8 = 14). Atomen met hetzelfde aantal protonen, maar met een verschillend aantal neutronen noemen we isotopen. Koolstof-12 en koolstof-14 zijn dus twee isotopen van koolstof.
$$^{12}_{\;6}C \;\;\;\;\;\; ^{14}_{\;6}C$$Ook het proton, het neutron en het elektron kunnen we in deze notatie opschrijven. Het proton bestaat uit 1 proton en 0 neutronen, dus het atoomnummer is 1 en het massagetal is ook 1. Het neutron bestaat uit 0 protonen en 1 neutron, dus het atoomnummer is 0 en het massagetal is 1. Het elektron vormt een uitzondering op de regel. Een elektron bevat natuurlijk 0 protonen, maar omdat het een lading van -1 heeft, zeggen we dat het atoomnummer -1 heeft. Het massagetal van een elektron is 0.
| $$^1_1p \;\;\;\;\;\;\;\; ^1_0n \;\;\;\;\;\;\;\; ^{\;\;0}_{-1}e$$ |
We spreken van een kernreactie als de atoomkern een verandering ondergaat. Een voorbeeld van een kernreactie is kernverval. Dit is het spontaan uit elkaar vallen van een atoomkern. Stoffen waarbij dit gebeurt noemen we radioactief. Bij kernverval schiet er vaak een deeltje met behoorlijke snelheid uit de atoomkern weg. We noemen dit straling. Als een atoom straling uitgezonden heeft, dan zeggen we dat het atoom vervallen is. De oorspronkelijke radioactieve kern noemen we de moederkern en de kern die na de straling overblijft noemen we de dochterkern. In sommige gevallen zijn de dochterkernen zelf ook weer radioactief. Er bestaan ook atoomkernen die geen straling uitzenden. We noemen deze isotopen stabiel.
Er kunnen bij kernreacties drie soorten straling vrijkomen. Welk type straling wordt uitgezonden door welke isotoop kan je vinden in BINAS.
Alfastraling
De eerste soort straling wordt alfastraling (α-straling) genoemd. Hierbij breekt een helium-4-kern af van de kern van een atoom (zie de onderstaande afbeelding). Een helium-4-kern bevat twee protonen en twee neutronen:
| $$^4_2He \;\;\;\;\;\;\;\; (\alpha)$$ |
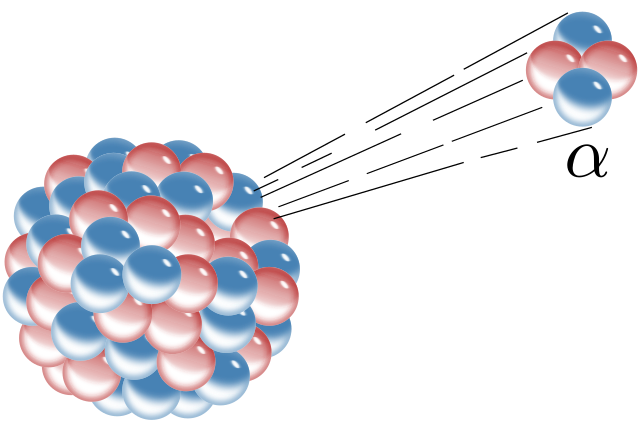
Laten we als voorbeeld het verval van de stof polonium-214 bestuderen. Volgens BINAS is polonium-214 een α-straler. We schrijven het verval van polonium-214 uit met een zogenaamde vervalvergelijking. In deze vergelijking schrijven we voor de pijl de stof die vervalt en achter de pijl de stoffen die na het verval zijn ontstaan. Omdat polonium-214 een alfastraler is, weten we in ieder geval dat er helium-4 is ontstaan:
$$ ^{214}_{84}\text{Po} \rightarrow ... + ^{4}_{2}\text{He} $$Zoals je ziet is de dochterkern die ontstaat nog onbekend. Om hier achter te komen gebruiken we het volgende.
De som van de atoomnummers voor de reactie moet gelijk zijn aan de som van de atoomnummers na de reactie. Hetzelfde geldt voor de massagetallen. Het behoud van atoomnummer is een gevolg van het behoud van lading. Het behoud van massagetal is het gevolg van het behoud van massa. We vinden hiermee:
$$ ^{214}_{84}\text{Po} \rightarrow ^{210}_{82}... + ^{4}_{2}\text{He} $$Zoals je ziet heeft de onbekende dochterkern atoomnummer 82 en massagetal 210. In BINAS kunnen we nu opzoeken welke stof hoort bij het atoomnummer 82. We vinden hier lood (Pb). De vergelijking wordt dus:
$$^{214}_{84}\text{Po} \rightarrow ^{210}_{82}\text{Pb} + ^{4}_{2}\text{He}$$Bètastraling
De tweede soort straling is bètastraling (β-straling), ook wel bèta-min-straling (β—straling) genoemd. In dat geval komt er een elektron uit de kern (zie de onderstaande afbeelding):
| $$^{\;\;0}_{-1}e^- \;\;\;\;\;\;\;\; (\beta^- \; \text{of} \;\; \beta)$$ |

Maar hoe kan er een elektron uit de kern komen? In sommige gevallen kan een neutron vervallen in een proton. Hier komt dan een elektron bij vrij:
$$^{1}_{0}\text{n} \;\rightarrow\; ^{1}_{1}\text{p} \;+\; ^{0}_{-1}\text{e}^-$$Laten we als voorbeeld het verval van kalium bestuderen. Volgens BINAS komt hier β--straling bij vrij:
$$ ^{40}_{19}\text{K} \;\rightarrow\; ... \;+\; ^{0}_{-1}\text{e}^- $$Ook hier moeten de atoomnummers en de massagetallen voor en na de reactie gelijk blijven. Houd er hier rekening mee dat het atoomnummer van het elektron -1 is. We vinden hiermee:
$$ ^{40}_{19}\text{K} \;\rightarrow\; ^{40}_{20}... \;+\; ^{0}_{-1}\text{e}^- $$In BINAS kunnen we nu opzoeken welke stof hoort bij het atoomnummer 20. We vinden hier calcium (Ca):
$$^{40}_{19}\text{K} \;\rightarrow\; ^{40}_{20}\text{Ca} \;+\; ^{0}_{-1}\text{e}^-$$
 Demonstratievideo
Demonstratievideo
| ||
|
 Demonstratievideo
Demonstratievideo
| ||
|
VWO-ers moeten ook weten van het bestaan van β+-straling. In dat geval komt er een positron uit de kern. Een positron heeft dezelfde eigenschappen als het elektron, behalve dat het een positieve lading heeft. We noemen dit het antideeltje van het elektron.
| $$^0_1e^+ \;\;\;\;\;\;\;\;\;\; (\beta^+)$$ |
Het positron ontstaat als een proton vervalt in een neutron:
$$^{1}_{1}\text{p} \; \rightarrow \; ^{1}_{0}\text{n} \;+\; ^{0}_{1}\text{e}^+$$Hieronder zien we een voorbeeld van een vervalvergelijking waar β+-straling bij vrij komt:
$$^{22}_{11}\text{Na} \;\rightarrow\; ^{22}_{10}\text{Ne} \;+\; ^{0}_{1}\text{e}^+$$Gammastraling
De laatste soort straling is gammastraling (γ-straling). Gammastraling bestaat uit lichtdeeltjes, ook wel fotonen genoemd, met een frequentie buiten het zichtbare spectrum. We schrijven:
| $$^0_0\gamma$$ |
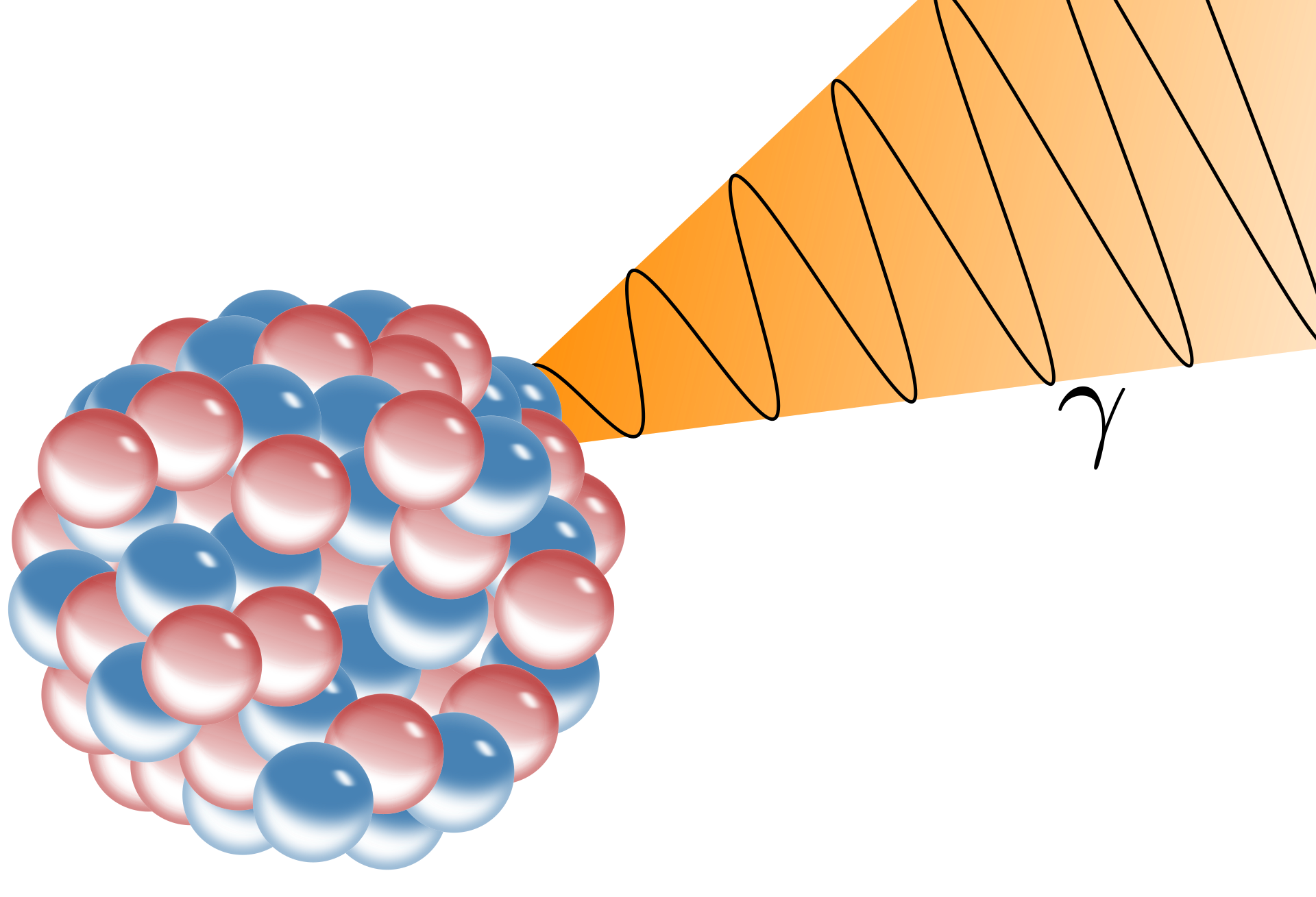
Zoals je ziet heeft een foton geen atoomnummer en ook geen massagetal. Als een atoomkern gammastraling uitzendt, verandert het atoomnummer en het massagetal dus niet. De kern raakt dan alleen wat energie kwijt. Als een kern alleen gammastraling kan uitstralen, dan noteren we naast het massagetal een "m". Dit geldt bijvoorbeeld voor technetium-99m. De kernvervalvergelijking ziet er dan als volgt uit:
$$ ^{99m}_{43}\text{Tc} \;\rightarrow\; ^{99}_{43}\text{Tc} \;+\; ^{0}_{0}\gamma $$Met de frequentie (f) van een foton kan als volgt de bijbehorende fotonenergie (Ef) berekend worden:
$$ E_f = hf $$
|
In het hoofdstuk "Trillingen" zijn we de formule f = v/λ tegengekomen. Deze formule kunnen we ook toepassen op het foton. Als we voor de snelheid de lichtsnelheid (c) invullen, dan kunnen we de bovenstaande formule omschrijven tot:
$$E_f = h\frac{c}{\lambda}$$
|
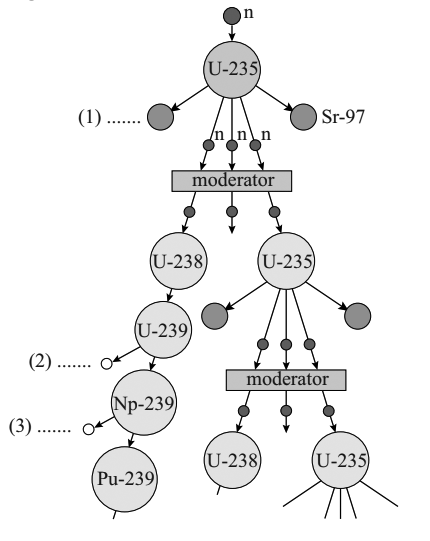
Tot nu toe hebben we het gehad over reacties die spontaan plaatsvinden. We kunnen kernreacties echter ook kunstmatig opwekken. Een voorbeeld is het beschieten van een uraniumatoom met een neutron. Het neutron wordt dan ingevangen door de kern, waarna de kern in een aantal stukken uiteenvalt. We noemen dit ook wel kernsplijting:
$$^{235}_{\;92}\text{U} \;+\; ^1_0\text{n} \;\rightarrow \;^{99}_{42}\text{Mo} \;+\; ^{134}_{\;50}\text{Sn} + 3^1_0\text{n}$$Zoals je kunt zien komen bij deze reacties weer nieuwe neutronen vrij en deze neutronen kunnen weer tegen andere uraniumatomen botsen. Als gevolg kan een kettingreactie op gang gebracht worden waarbij heel veel energie vrijkomt. Een gecontroleerde versie van zo'n kettingreactie vindt plaats in een kernreactor (en een ongecontroleerde versie bij het ontploffen van een kernbom).
De werking van een kernreactor is hieronder aan de linker zijde simpel weergegeven. Het radioactieve materiaal, hier de kernbrandstof genoemd, zorgt ervoor dat een omringend gas wordt opgewarmd (hier in het geel aangegeven). Dit hete gas zorgt er op zijn beurt weer voor dat water aan de kook wordt gebracht. De stoom die hierbij ontstaat wordt gebruikt om een turbine te laten draaien waarmee elektriciteit wordt gegenereerd (dit deel is niet afgebeeld). Door middel van regelstaven, die in en uit de kernbrandstof kunnen worden geschoven, kan de reactie beperkt of juist versterkt worden. De toren die rechts is afgebeeld wordt gebruikt om het systeem te koelen, zodat het niet oververhit raakt. De nevel die aan de bovenzijde opstijgt bestaat uit water.
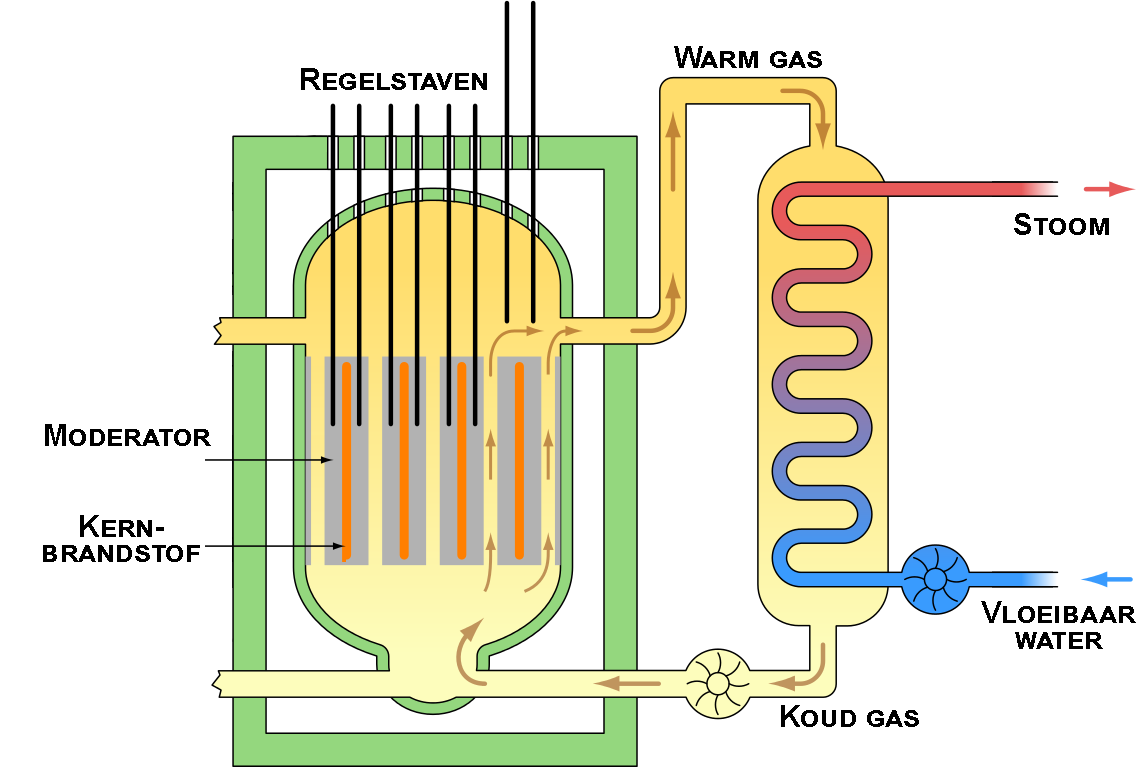
 (Afbeelding: Emoscopes; CC BY-SA 3.0 / Bjoern Schwarz; CC BY 2.0)
(Afbeelding: Emoscopes; CC BY-SA 3.0 / Bjoern Schwarz; CC BY 2.0)
De kans dat een vrijkomend neutron daadwerkelijk een volgende uraniumkern kan doen splijten, hangt van een aantal dingen af. Belangrijk is o.a. de snelheid van de neutronen. Te snelle neutronen zijn maar kort in de buurt van de atoomkernen en hebben daarom een kleinere kans om deze kern te doen splijten. In een kerncentrale wordt dit probleem opgelost met een moderator. Dit is een stof die ervoor zorgt dat neutronen afremmen. De meest voorkomende moderator is water.
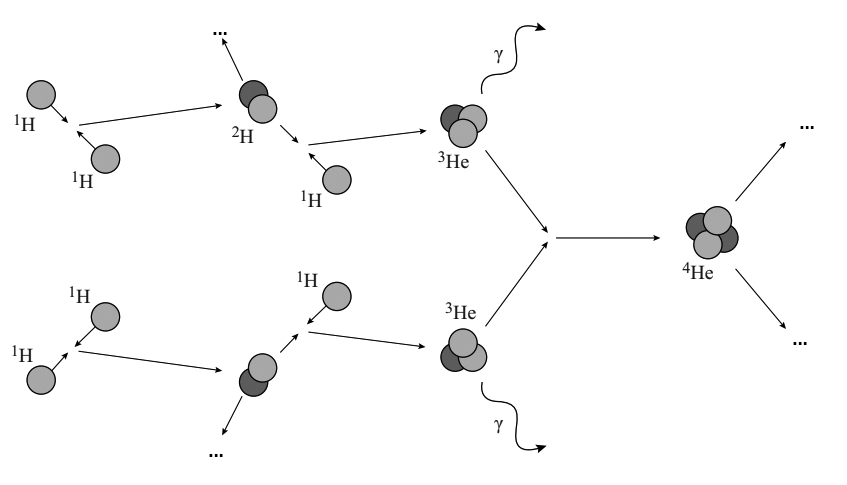
Naast kernverval bestaat ook kernfusie. Hier fuseren atoomkernen samen. Ook bij dit proces kan energie vrijkomen. Dit gebeurt bijvoorbeeld in de zon. Hier wordt waterstof gefuseerd tot helium. De energie die hierbij vrijkomt zorgt voor het licht dat de zon geeft.
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§2 Halveringstijd
In deze paragraaf gaan we bestuderen hoe het aantal radioactieve deeltjes in een bron afneemt in de tijd. We gebruiken hiervoor het begrip halveringstijd.
In de vorige paragraaf hebben we gezien dat radioactieve atoomkernen naar verloop van tijd straling uitzenden. Als dit gebeurt is, dan zeggen we dat het atoom vervallen is. De tijdsduur waarna de helft van de deeltjes in de bron vervallen is, noemen we de halveringstijd of de halfwaardetijd (t1/2).
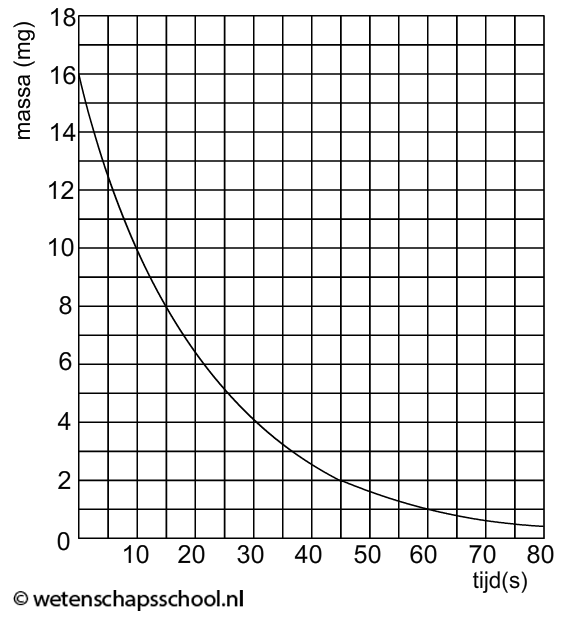
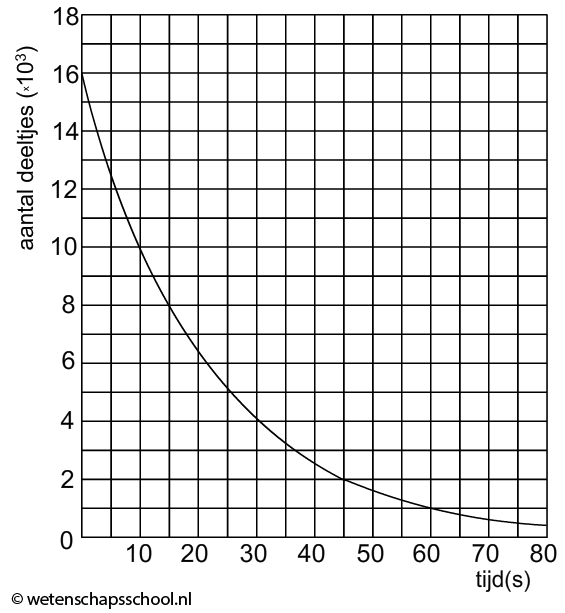
In het onderstaande (N,t)-diagram zien we het aantal radioactieve deeltjes in een bron (N) uitgezet tegen de tijd (t). In dit geval zien we dat het aantal radioactieve kerndeeltjes elke 10 uur halveert. Voor deze bron geldt dus een halveringstijd van 10 uur.
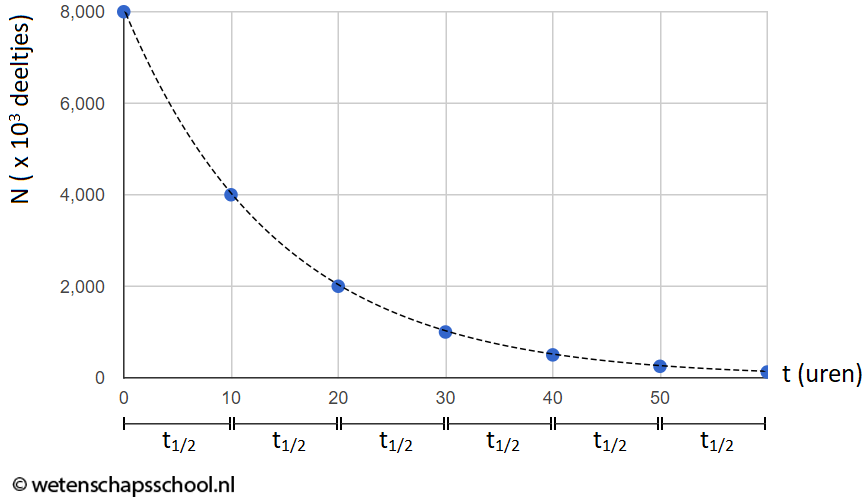
In het onderstaande programma zien we hoe deze grafiek zijn vorm krijgt. Elke keer als je op de knop "+1 halfwaardetijd" klikt, geldt voor elk radioactief deeltje (aangegeven met een zwarte cirkel) dat deze 50% kans heeft om te vervallen (een vervallen deeltje wordt weergegeven als een witte cirkel).
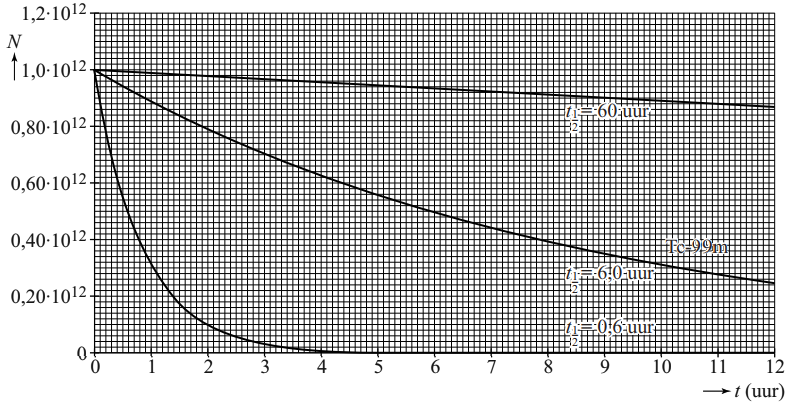
Elke radioactieve isotoop heeft zijn eigen halveringstijd en deze kan variëren van een fractie van een seconde tot miljoenen jaren. Voor een aantal isotopen is de halveringstijd te vinden in BINAS. In deze tabel vinden we bijvoorbeeld dat koolstof-14 een halveringstijd heeft van 5730 jaar. Na 5730 jaar is dus nog maar 50% van de koolstof-14 over. Na 2 × 5730 = 11 460 jaar is 25% over en na 3 × 5730 = 17 190 jaar is nog slechts 12,5%. Etc.
Het aantal radioactieve deeltjes waaruit een bron bestaat op tijdstip t = 0 noemen we N0. Het aantal radioactieve deeltjes dat nog over is een tijdstip t later noemen we Nt. Als een stof in deze tijd bijvoorbeeld 3x gehalveerd is, dan geldt:
$$N_t = N_0 \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}$$Dit korten we af tot:
$$N_t = N_0 \left( \frac{1}{2} \right)^{3}$$Als we het aantal halveringen "n" noemen, dan kunnen we dit algemener opschrijven als:
$$N_t = N_0 \left( \frac{1}{2} \right)^{n}$$
|
 VWO-stof
VWO-stof
|
|
Als we het aantal halveringstijden (n) willen uitrekenen, dan moeten we de formule omschrijven in de onderstaande vorm:
$$\frac{\log{(N_t/N_0)}}{ \log{(1/2) }} = n$$
|
 Extra
Extra
|
|
Als we de tijd of de halveringstijd willen uitrekenen, dan moeten we gebruik maken van het logaritme. Eerst nemen we aan beide kanten de logaritme: $$ \log{\frac{N_t}{N_0}} = \log{\left( \frac{1}{2} \right)^{\frac{t}{t_{1/2}}}} $$De macht kan nu uit de logaritme gehaald worden: $$ \log{\frac{N_t}{N_0}} = \frac{t}{t_{1/2}} \times \log{\left( \frac{1}{2} \right)} $$Als we dit omschrijven, dan vinden we:
$$ \frac{\log{(N_t/N_0)}}{ \log{(1/2) }} = \frac{t}{t_{1/2}} $$
|
De formule wordt ook vaak herschreven tot:
| $$\frac{N_t}{N_0} = \left( \frac{1}{2} \right)^{n}$$ |
De linkerkant van de vergelijking geeft nu de fractie van het aantal deeltjes dat nog over is op tijdstip t. Als we de fractie met 100 vermenigvuldigen, dan vinden we het percentage. Als bijvoorbeeld geldt dat Nt/N0 = 0,09, dan weten we dus dat nog 9% van de kernen over is.
Het aantal halveringen (n) kunnen we ook uitrekenen door de tijd t te delen door de halveringstijd:
$$n = \frac{t}{t_{1/2}}$$
|
Doordat in deze formule twee tijden door elkaar worden gedeeld, ben je niet gebonden aan de seconde. Je kan beide tijden dus ook best in bijvoorbeeld dagen of jaren invullen.
De halveringstijd van stoffen kan o.a. gebruikt worden voor radiometrische datering. Dit is een techniek die gebruikt wordt om uit te vinden hoe oud voorwerpen zijn. Het bekendste voorbeeld hiervan is C14-datering. Koolstof-14 komt in vergelijking met andere koolstofisotopen in elk levend organisme in een vaste verhouding voor. Als een organisme echter sterft, komt er geen nieuwe koolstof-14 binnen, maar neemt de overgebleven koolstof-14 wel af door kernverval. Door te kijken hoeveel koolstof-14 er nog over is, kunnen we met de halveringstijd uitrekenen hoe lang geleden het organisme gestorven is.
 Voorbeeld (HAVO)
Voorbeeld (HAVO)
|
|
Vraag: Opdracht (HAVO): Antwoord: De 6,25% wordt dus behaald na 4 halveringen. Dan zoeken we de halveringstijd van C-14 op in BINAS. Er geldt: t1/2 = 5730 j Hiermee kunnen we uitrekenen hoe oud het beeldje is: $$t = t_{1/2} \times n $$ $$t = 5730 \times 4 = 22,9 \times 10^3 \text{ jaar}$$In dit geval blijkt het deeltje uit de Oude Steentijd te komen!
|
 Voorbeeld (VWO)
Voorbeeld (VWO)
|
|
Opdracht (VWO): Antwoord: Zoals we hierboven gelezen hebben, staat Nt/N0 voor de fractie van het aantal deeltjes dat is overgebleven (in dit geval is dat 6,25% / 100 = 0,0625). Als we dit invullen, dan vinden we: $$\frac{\log{(0,0625)}}{ \log{(1/2) }} = 4 $$Dan zoeken we de halveringstijd van C-14 op in BINAS. Er geldt: t1/2 = 5730 j Hiermee kunnen we uitrekenen hoe oud het beeldje is: $$t = t_{1/2} \times n $$ $$t = 5730 \times 4 = 22,9 \times 10^3 \text{ jaar}$$In dit geval blijkt het deeltje uit de Oude Steentijd te komen!
|
Ten slotte leren we in het onderstaande voorbeeld hoe we met de massa van een radioactieve stof het aantal deeltjes kunnen uitrekenen waaruit de stof bestaat. We gaan dit in dit hoofdstuk nog veelvuldig nodig hebben.
 Voorbeeld
Voorbeeld
|
|
Vraag: Bereken het aantal kernen in 12 μg uranium-238. Antwoord: We zoeken eerst in BINAS de atoommassa van U-238 op: $$m = 238,05 \text{ u}$$De u is hier de zogenaamde atomaire massa-eenheid. In BINAS kan je ook vinden dat geldt: $$1 \text{ u} = 1,6605 \times 10^{-27} \text{ kg}$$Voor één U-238-kern vinden we dan: $$238,05 \times 1,6605 \times 10^{-27} = 3,9528 \times 10^{-25} \text{ kg}$$Als we nu het aantal deeltjes willen weten in 12 μg Uranium-238, dan delen we deze massa door de massa van één kern. We vinden: $$\frac{12 \times 10^{-9}}{3,9528 \times 10^{-25}} = 3,0 \times 10^{16} \text{ kernen}$$We hebben hier gebruikt dat: We hebben hier gebruikt dat 12 μg = 12 × 10-6 g = 12 × 10-9 kg.
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§3 Activiteit
De activiteit is een maat voor de hoeveelheid kernen die per tijdseenheid vervalt. In deze paragraaf gaan we leren hoe we de activiteit van een radioactieve bron kunnen bepalen met behulp van een geigerteller.
Het aantal deeltjes dat per tijdseenheid vervalt noemen we de activiteit (A). De SI-eenheid van de activiteit is de becquerel (Bq). Becquerel staat voor het aantal deeltjes dat per seconde vervalt. We kunnen de activiteit berekenen met de volgende formule:
$$A_t = -\frac{\Delta N}{\Delta t}$$
|
De activiteit op een bepaald tijdstip kunnen we bepalen door een raaklijn te tekenen in een (N,t)-diagram. Dit is hieronder gedaan. Omdat de raaklijn naar beneden loopt vinden we een negatieve waarde. Door de extra min in de formule wordt de activiteit toch positief.
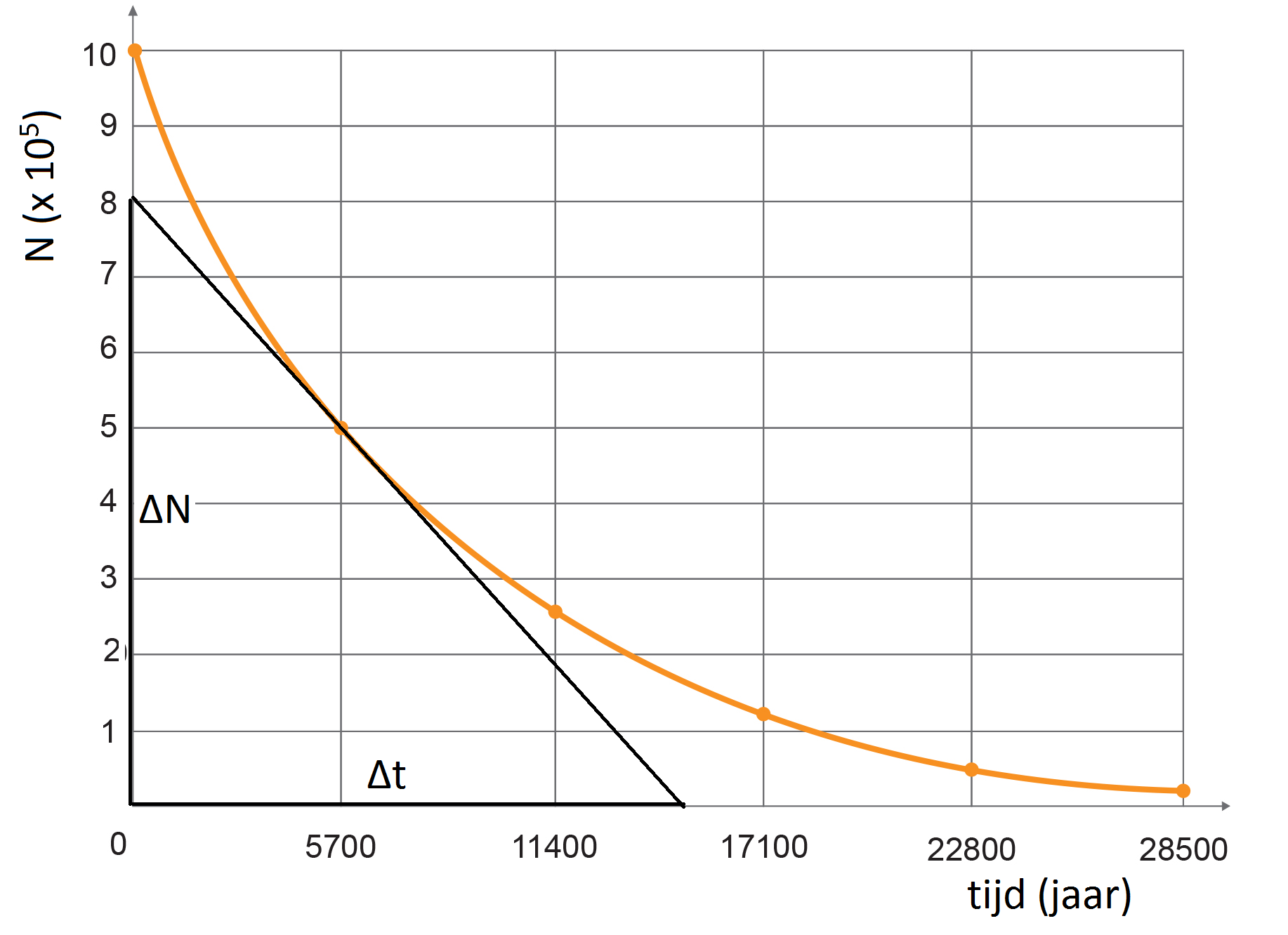
De activiteit neemt gedurende de tijd af volgens de volgende formule:
$$A_t = A_0 \left( \frac{1}{2} \right)^{n}$$
|
Deze formule kan je in dezelfde vormen omschrijven als de formule "Nt = N0(1/2)n" in de vorige formule.
Ook bij deze formule hoort een grafiek (zie de onderstaande afbeelding). Het oppervlak onder een (A,t)-grafiek is gelijk aan het aantal vervallen deeltjes (ΔN).
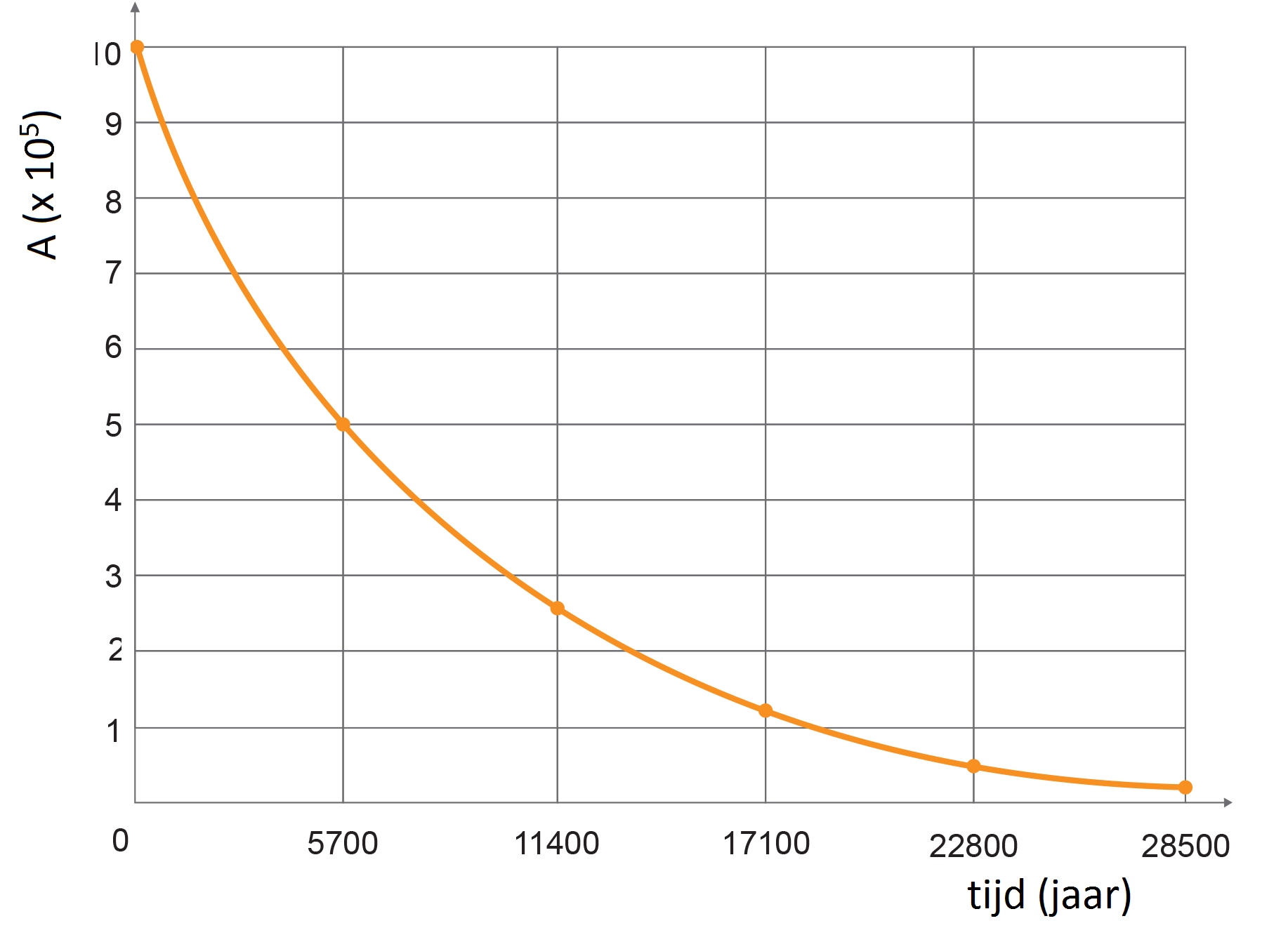
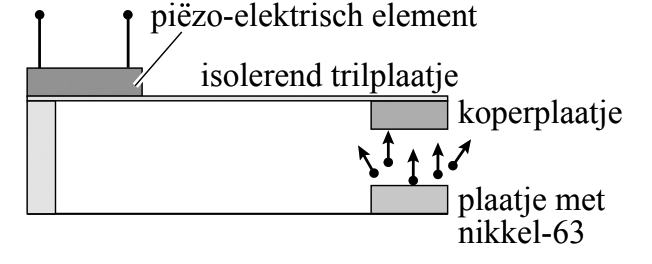
We kunnen we activiteit van een bron bepalen met een geigerteller (zie de onderstaande afbeelding). Dit apparaat bestaat uit een buis met daarin een gas. Als straling het gas binnenkomt, dan worden een aantal atomen van het gas geïoniseerd. Dit betekent dat de straling elektronen uit de atomen van het gas trekt. De vrijgemaakte elektronen zorgen dan voor een kleine stroom en deze stroom zorgt in een luidspreker voor een hoorbaar piepje. Hoe meer piepjes je hoort, hoe meer straling er in de buurt is.
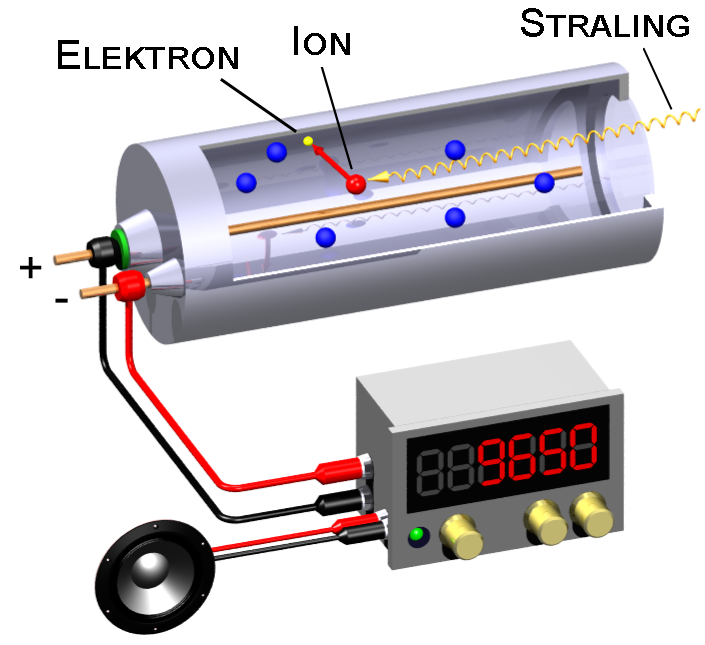 (Afbeelding: ... / Svjo-2; CC BY-SA 2.0)
(Afbeelding: ... / Svjo-2; CC BY-SA 2.0)
 EXPERIMENT
EXPERIMENT
|
| In deze filmpjes wordt de geigerteller gedemonsteerd. In het eerste filmpje zien we dat een type bord dat vroeger gebruikt werd radioactief materiaal bevat. In het tweede filmpje kan je aan het begin de achtergrondstraling horen. Later in het filmpje wordt de geigerteller bij een radioactieve bron gebracht. |
Zelfs als je een geigerteller niet bij een bron houdt, zal je af en toe een piepje horen. Dit komt doordat radioactieve stoffen in kleine hoeveelheden voorkomen in veel voorwerpen om ons heen. We noemen dit de achtergrondstraling. Als we metingen verrichten met een geigerteller, dan is het noodzakelijk eerst de gemiddelde achtergrondstraling te meten. Als je metingen doet aan een bron, dan moet je deze achtergrondstraling van de meting afhalen, zodat je alleen de bron meet.
 Voorbeeld (VWO)
Voorbeeld (VWO)
|
|
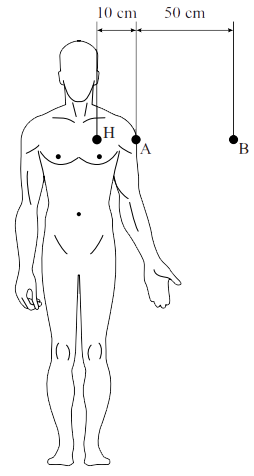
Opdracht: Met een geigerteller kan de activiteit van een radioactieve bron bepaald worden. Nog voordat de bron geplaatst wordt, meet de teller al 15 deeltjes per minuut aan achtergrondstraling. De bron wordt op een afstand van 10 cm van de geigerteller geplaatst in een vacuümruimte. Het meetoppervlak van de teller is cirkelvormig en heeft een straal van 2,0 cm. Met de bron erbij meet de teller 35 deeltjes per minuut. Bereken de activiteit van de bron. Antwoord: Ten eerste halen we de achtergrondstraling af van de straling die in de teller terecht kwam. We houden dan nog 35 – 15 = 20 deeltjes per minuut over. Als we dit delen door 60, dan vinden we het aantal deeltjes dat per seconde aankomt bij de teller: $$ A = \frac{\Delta N}{\Delta t} \;\;\;\;\;\;\;\;\;\;\;\; A = \frac{20}{60} = 0,333 \text{ Bq} $$Dan berekenen we het cirkelvormige meetoppervlak van de geigerteller. De straal is gelijk aan 2 cm = 0,02 m. Hiermee vinden we: $$ O_{geiger} = 4\pi r^2 = 4\pi \times 0,02^2 = 0,005027 \text{ m}^2 $$De bron straalt echter in alle richtingen. Het totale oppervlak dat bestraald wordt op een afstand van 10 cm is: $$ O_{tot} = 4\pi r^2 = 4\pi \times 0,10^2 = 0,12566 \text{ m}^2 $$Dit oppervlak is 0,12566 / 0,005027 = 25 keer zo groot als het meetoppervlak van de geigerteller. De totale activiteit wordt hiermee: $$ A = 25 \times 0,333 = 8,3 \text{ Bq} $$
|
 VWO-stof
VWO-stof
| |||||||
|
We kunnen de activiteit op een tijdstip t ook uitrekenen met het aantal radioactieve deeltjes N op datzelfde tijdstip. Hiervoor gebruiken we de volgende formule:
Belangrijk is dat bij deze formule de tijd altijd in seconde gegeven moet worden.
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§4 Stralingsgevaar
In deze paragraaf bestuderen we de gevaren van straling voor de mens.
Als radioactieve straling met genoeg kinetische energie een atoomkern verlaat, dan kan het andere atomen ioniseren (dit betekent dat er elektronen uit deze atomen getrokken worden). De mate waarin straling in staat is andere atomen te ioniseren noemen we het ioniserend vermogen. Ioniserende straling kan schadelijk zijn voor de gezondheid. Het kan bijvoorbeeld het DNA beschadigen en dit kan het begin zijn van een tumor. Het is dus belangrijk dat we in omgang met radioactieve bronnen goede voorzorgsmaatregelen treffen.
Er zijn twee manieren waarop je schade kan ondervinden van straling. De eerste is bestraling. Bij bestraling bevindt de radioactieve bron zich buiten het lichaam en ondervindt het lichaam schade door de straling die uit deze bron schiet. Als deze deeltjes echter hun impact gemaakt hebben, dan zijn ze verder onschadelijk. Als je dus van de bron wegloopt, dan neemt de schade niet toe. De straling zelf is immers niet radioactief. Bij besmetting komt de radioactieve bron in het lichaam terecht. Het is dus niet mogelijk om van deze bron weg te lopen. Besmetting is daarom over het algemeen gevaarlijker dan bestraling.
De schadelijke gevolgen van straling zijn afhankelijk van de energie van de straling en de massa van het lichaamsdeel dat de straling ontvangt. In formuletaal schrijven we dit als volgt op:
$$D = \frac{E_{straling}}{m}$$
|
De totale stralingsenergie die het lichaamsdeel ontvangt is gelijk aan de energie van één deeltje maal de hoeveelheid vervallen deeltjes:
$$E_{straling} = \Delta N \times E_{deeltje}$$
|
De stralingsenergie per deeltje is voor veel isotopen te vinden in BINAS. Er wordt hier de eenheid elektronvolt (eV) gebruikt. Er geldt:
$$1 \text{ eV} = 1,6 \times 10^{-19} \text{ J}$$Ook wordt vaak mega-elektronvolt (MeV) gebruikt. Hier geldt:
$$1 \text{ MeV} = 10^6 \times 1,6 \times 10^{-19} \text{ J} = 1,6 \times 10^{-13} \text{ J}$$Ook het type straling heeft invloed op het ioniserend vermogen. Door de relatieve grote massa en lading van alfastraling is het grofweg 20x schadelijker dan bèta- of gammastraling. We corrigeren voor dit effect door de stralingsdosis te vermenigvuldigen met de zogenaamde stralingsweegfactor (wR). Deze factor is gelijk aan 1 voor gamma- en bètastraling en gelijk aan 20 voor alfastraling. Het resultaat noemen we de equivalente dosis (H), gemeten in sievert (Sv):
$$H = w_R D$$
|
Voor de veiligheid zijn er stralingsbeschermingsnormen opgesteld. Dit is de maximale effectieve dosis in millisievert per jaar die is toegestaan. Deze normen zijn te vinden in BINAS.
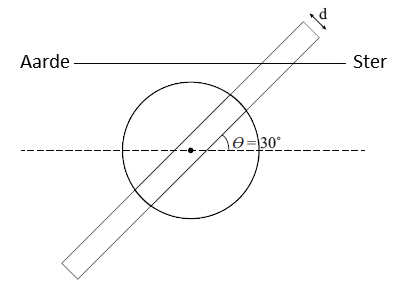
Mensen die werken met radioactieve stoffen dragen vaak een badge. Een badge maakt gebruik van het verschil in doordringend vermogen van de verschillende typen straling. Hoe hoger het doordringend vermogen, hoe gemakkelijker de straling door materialen heendringt. De daadwerkelijke afstand die straling aflegt als het een stof binnendringt, noemen we de dracht. Alfastraling heeft een klein doordringend vermogen en dus ook de kleine dracht. Zelfs door lucht kan alfastraling slechts enkele centimeters voortbewegen. Bètastraling heeft een groter doordringend vermogen en dat van gammastraling is het grootst. Gammastraling wordt door de lucht nauwelijks geabsorbeerd en een deel van gammastraling kan zelfs dwars door het lichaam heen bewegen. In de onderstaande linker afbeelding zien we een doorsnede van de badge. Het linker deel van de badge laat alle soorten straling door. Het middelste deel laat bèta- en gammastraling door en het rechter deel alleen gammastraling. De straling die doorgelaten wordt komt tegen een film aan die verkleurt door deze straling. Door de verkleuring op de drie plekken te vergelijken, kan je voor elk type straling achterhalen aan hoeveel straling de badge (en dus de persoon) heeft blootgestaan.
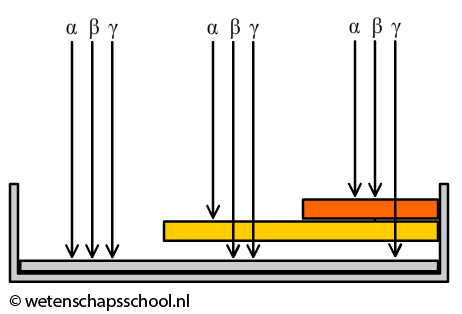
 Demonstratievideo
Demonstratievideo
| ||
|
 Demonstratievideo
Demonstratievideo
| ||
|
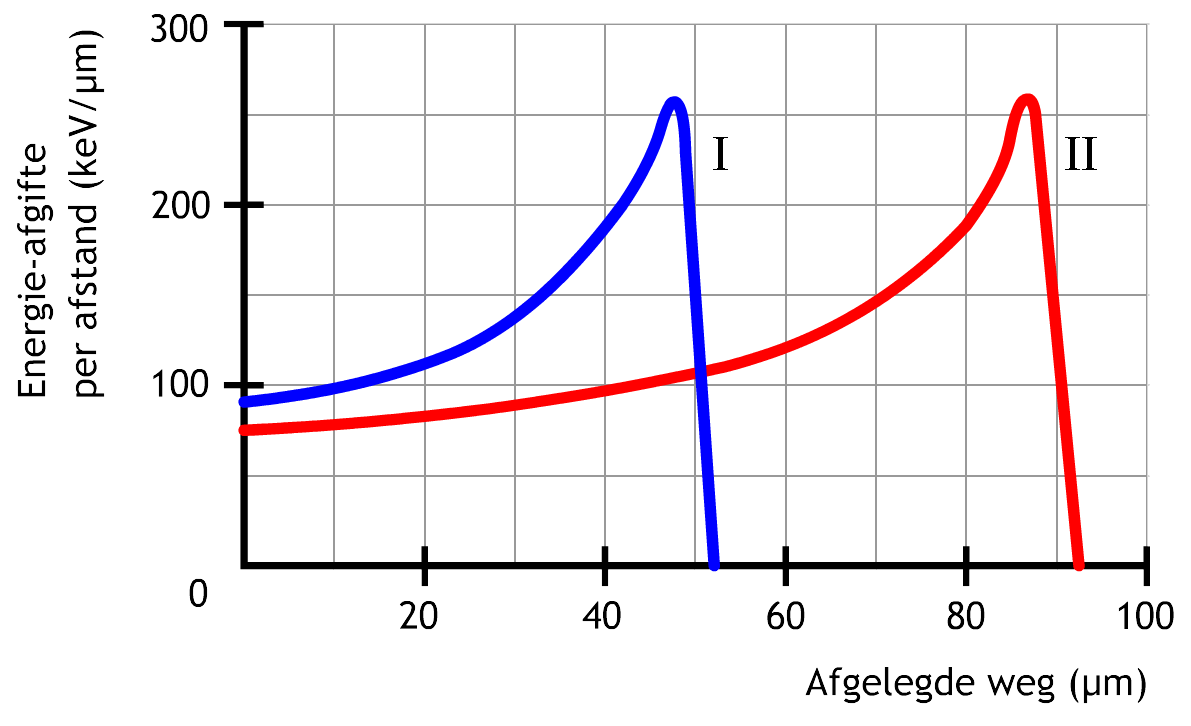
Het doordringend vermogen van alfa- en bèta-straling is ook afhankelijk van de beginsnelheid waarmee deze deeltjes een materiaal inschieten. In het onderstaande diagram is voor alfadeeltjes met twee verschillende beginsnelheden weergegeven hoever ze doordringen in water. Op de horizontale as staat de afgelegde weg van de deeltjes. Op de verticale as staat de hoeveelheid energie die elk deeltje per eenheid van afgelegde weg heeft afgegeven door botsing met de deeltjes in het materiaal. Merk op dat beide deeltjes aan het begin weinig energie afgeven. Aan het begin bewegen de deeltjes namelijk het snelst, waardoor ze maar kort in de buurt blijven van de deeltjes in het materiaal, wat de kans op botsing verlaagd. Deeltje II moet een grotere beginsnelheid hebben gehad. Dit weten we omdat dit deeltje verder doordringt in het water en ook omdat het deeltje aan het begin van de beweging minder energie kwijtraakte (en dus een grotere snelheid gehad moet hebben).
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
| ||||||||||
|
§5 E = mc2
In deze paragraaf gaan we begrijpen hoe radioactieve stoffen als energiebron kunnen dienen. We bestuderen hiervoor de beroemde formule E = mc2.
In deze paragraaf gaan we begrijpen waar de energie vandaan komt die bij vervalreacties ontstaat. We bestuderen hiervoor de volgende kernreactie:
$$ ^{32}_{15}P \;\;\rightarrow \;\; ^{0}_{-1}e \;+\; ^{32}_{16}S $$Als we de massa's van de kerndeeltjes voor en na de reactie vergelijken, dan blijkt er massa verdwenen te zijn. De massa’s van verschillende isotopen zijn te vinden in BINAS. Deze massa’s zijn echter niet de massa’s van de atoomkern, maar van het gehele atoom. Om de massa van de kern te vinden moeten we hier de massa’s van de elektronen nog vanaf halen. Ook de massa van het elektron kunnen we in BINAS vinden (me = 0,00054858 u). In het geval van de bovenstaande vervalvergelijking vinden we de volgende massa's:
$$ m_{P-32} = 31,97391 \text{ u} - 15 \times 0,00054858 \text{ u} = 31,9656813 \text{ u} $$ $$ m_{e} = 0,00054858 \text{ u} $$ $$ m_{S-32} = 31,97207 \text{ u} - 16 \times 0,00054858 \text{ u} = 31,96329 \text{ u} $$Als we nu de totale massa voor de reactie vergelijken met de massa na de reactie, dan vinden we:
$$ \Delta m = m_{eind} - m_{begin}$$Aan het begin hebben we P-32 en aan het eind S-32 en een elektron. Er geldt dus:
$$ \Delta m = m_e + m_{S-32} - m_{P-32} $$ $$ \Delta m = 0,00054858 + 31,96329 - 31,9656813 = -0,00184272 \text{ u} $$Nu rekenen we de massa om naar kilogram (1 u = 1,6605389 × 1027 kg):
$$ \Delta m = 0,00184272 \times 1,6605389 \times 10^{-27} = 3,0599082 \times 10^{-30} \text{ kg} $$We kunnen hieruit concluderen dat er inderdaad massa verdwenen is tijdens de kernvervalreactie. We noemen de verdwenen massa het massadefect. Deze massa is omgezet in energie volgens de bekende formule van Einstein:
$$ E = mc^2 $$
|
Voor het bovenstaande voorbeeld vinden we:
$$ E = 3,0599082 \times 10^{-30} \times (2,997925 \times 10^8)^2 = 2,7501084 \times 10^{-13}\text{ J} $$Als we deze energie omschrijven van joule naar MeV, dan vinden we:
$$ E = \frac{2,7501084 \times 10^{-13}}{10^6 \times 1,602177 \times 10^{-19}} = 1,72 \text{ MeV} $$Dit komt dicht in de buurt van de waarde die we in BINAS vinden bij P-32.
Een andere situatie waarbij massa wordt omgezet in energie is bij de botsing van een elektron en een positron. Beide deeltjes worden dan geheel omgezet in energie. We noemen dit annihilatie. De energie komt in dit geval vrij in de vorm van twee fotonen:
$$ ^0_{-1}e^- \;+\; ^0_{1}e^+ \;\;\;\rightarrow\;\;\; ^0_0\gamma \;+\; ^0_0\gamma $$De frequentie (f) van deze fotonen kan worden berekend met de volgende formule:
$$ E_f = hf $$
|
In het hoofdstuk "Trillingen" zijn we de formule "f = v/λ" tegengekomen. Deze formule kunnen we ook toepassen op het foton. Als we voor de snelheid de lichtsnelheid (c) invullen, dan kunnen we de bovenstaande formule omschrijven tot:
$$E_f = h\frac{c}{\lambda}$$
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§6 Medische beeldvorming
Radioactieve stoffen worden o.a. gebruikt in ziekenhuizen bij het maken van scans van de binnenkant van het menselijk lichaam. Denk bijvoorbeeld aan de PET-scan. In deze paragraaf bespreken we ook een aantal andere typen scans, waaronder de MRI-scan, de röntgenscan en de echo.
Radioactieve stoffen worden veel gebruikt in het ziekenhuis om goede diagnoses te kunnen maken. Een bekende techniek is scintigrafie. Bij deze techniek wordt er een radioactieve stof, genaamd een tracer, in het lichaam gespoten. Deze stof hoopt zich op bepaalde plekken in het lichaam op en zendt hier gammastraling uit. Een deel van deze straling zal door het lichaam worden geabsorbeerd, maar er zal ook een deel zijn dat het lichaam zal verlaten, waarna het in een detector terecht komt. Met behulp van deze straling kan dan een foto van de binnenkant van het lichaam gemaakt worden.
 VWO-STOF
VWO-STOF
|
|
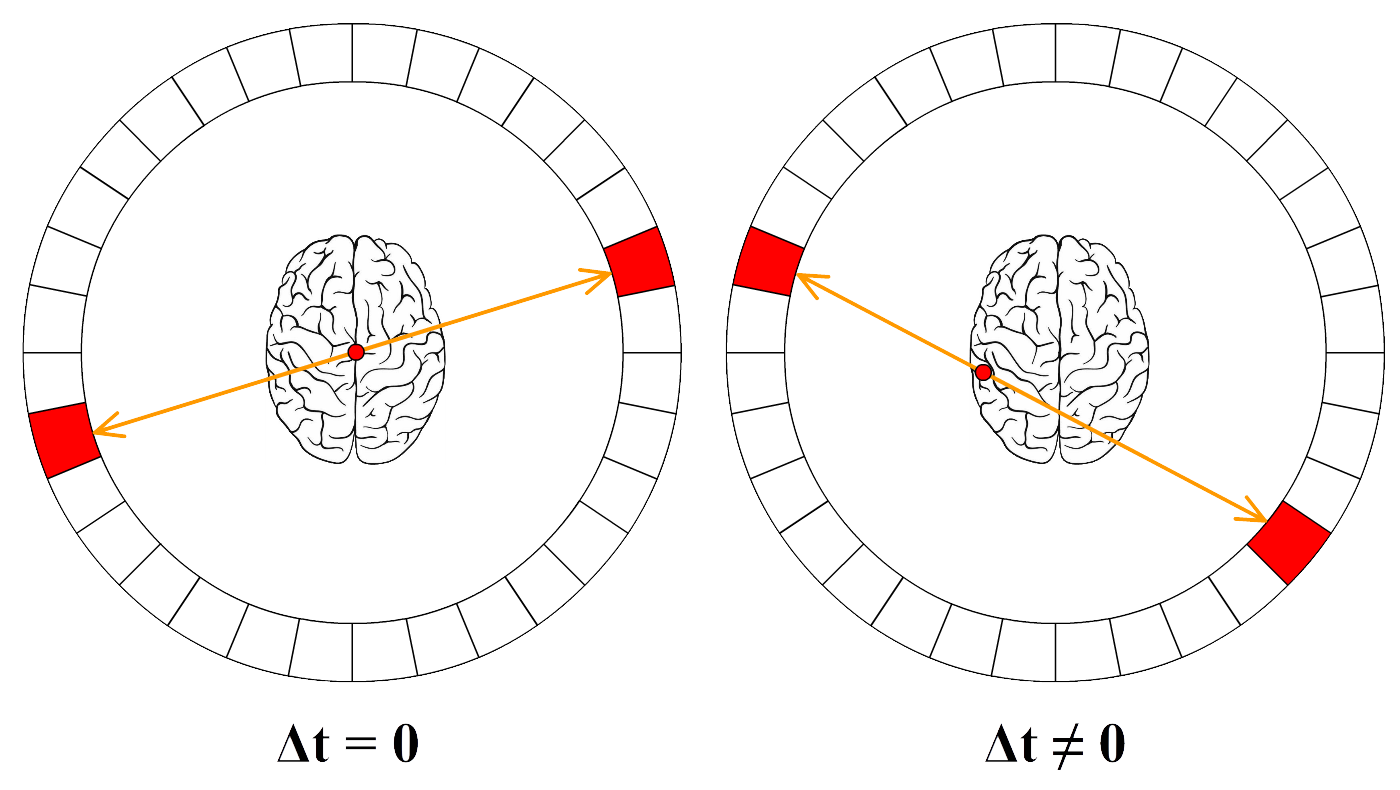
Een bekend voorbeeld hiervan is de PET-scan. De tracer bij een PET-scan zendt positronen uit. Als een positron tegen een elektron in het lichaam botst, dan worden beide deeltjes omgezet in twee fotonen die in tegengestelde richting wegschieten. We noemen deze reactie annihilatie: $$ ^0_{-1}e^- \;+\; ^0_{1}e^+ \;\;\;\rightarrow\;\;\; ^0_0\gamma \;+\; ^0_0\gamma $$Een deel van deze fotonen zal het lichaam verlaten en worden gedetecteerd door een cirkelvormige detector, zoals in de volgende afbeelding is weergegeven. Door het verschil in tijd te meten tussen de aankomst van beide fotonen, kan met de formule Δx = cΔt de positie van de annihilatie bepaald worden.
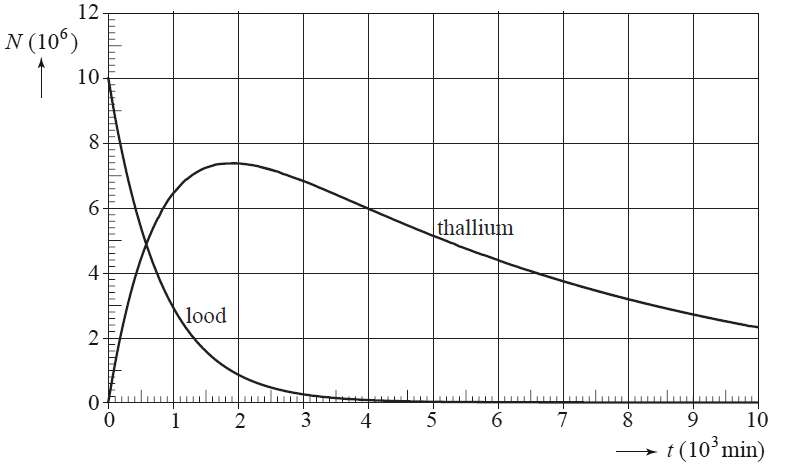
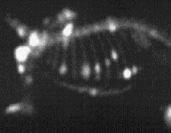
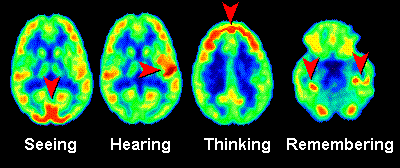
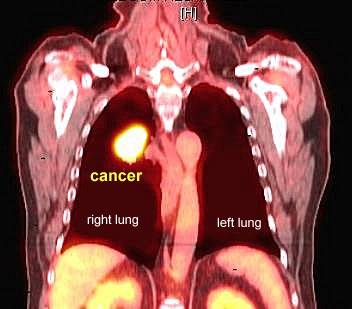
In de onderstaande linker afbeelding zien we PET-scans van de hersenen. Er is in dit geval als tracer radioactief glucose gebruikt. Hersendelen die meer actief zijn nemen meer glucose op en als gevolg lichten deze delen meer op in de PET-scan. Op deze manier kunnen we dus een idee krijgen van hersenactiviteit. Dezelfde methode kan ook gebruikt worden bij het opsporen van tumoren. Tumoren gebruiken namelijk relatief veel glucose en lichten daarom duidelijk op in de scan. In de rechter afbeelding zien we een tumor die oplicht in de longen. Een ander bekend voorbeeld is het gebruik van een jood-tracer voor het onderzoek naar de schildklier. De schildklier neemt relatief veel jood op en dit maakt de schildklier goed zichtbaar met een PET-scan.
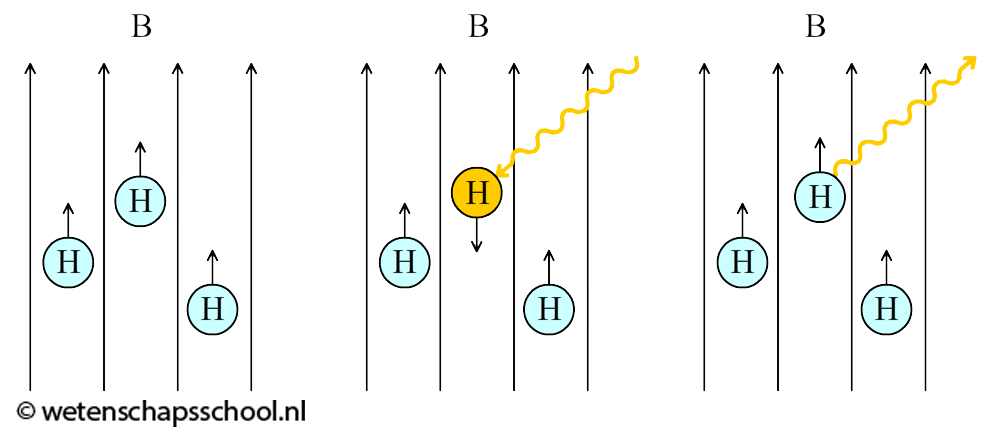
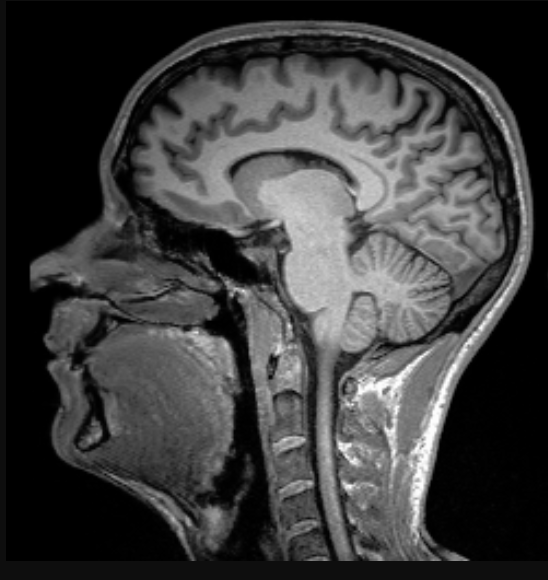
Een ander type scan die vaak gebruikt wordt om het lichaam in kaart te brengen is de MRI-scan. Bij het maken van een MRI-scan wordt een persoon in een magneetveld (B) gelegd. Waterstofatomen in het lichaam reageren op dit magneetveld. Waterstofatomen hebben namelijk een draairichting. Dit wordt ook wel de spin genoemd. De spin zorgt ervoor dat de atomen zich gedragen als kleine magneetjes die net als een kompasnaald in de richting van het magneetveld gaan staan (zie de onderstaande linker afbeelding). Daarna wordt het lichaam bestraald met fotonen. De frequentie van deze fotonen wordt zo gekozen dat ze precies genoeg energie hebben om waterstofatomen in een hogere energietoestand te brengen. De waterstofatomen komen hierbij tegen de richting van het magneetveld in te liggen (zie de tweede en de derde afbeelding). We noemen de frequentie waarbij dit gebeurt de resonantiefrequentie. De grootte van deze frequentie hangt af van de sterkte van het magneetveld. Na een korte tijd (de zogenaamde relaxatietijd) zal het waterstofatoom weer terugvallen naar zijn grondtoestand en hierbij wordt hetzelfde foton weer uitgezonden (zie de vierde afbeelding). Een deel van deze fotonen wordt buiten het lichaam gedetecteerd en hiermee wordt de foto gemaakt.
Waterstof atomen komen o.a. voor in water. Hoe meer water dus in een deel van het lichaam zit, hoe meer fotonen hier dus vandaan zullen komen. Met behulp van verschillen in de waterstofdichtheid kan het lichaam hiermee nauwkeurig in kaart worden gebracht (zie de onderstaande afbeelding).
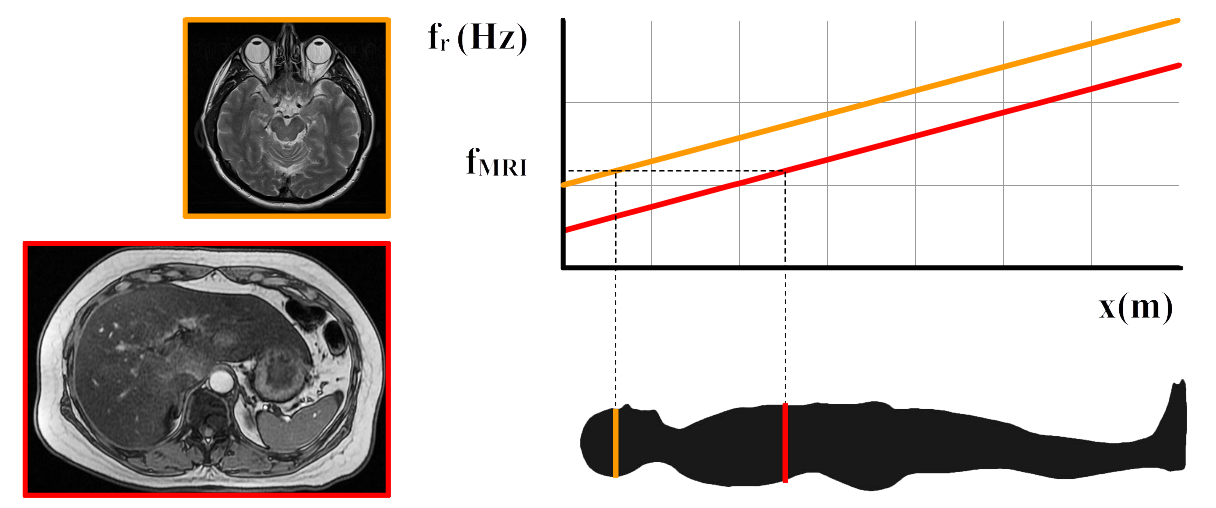
Voor het maken van goede scans kan ook gebruik worden gemaakt van het verschil in relaxatietijd van de waterstofkernen in verschillende soorten weefsel. Hier wordt verwezen naar de tijd die het een waterstofkern kost om terug te vallen naar zijn grondtoestand. Ook dit kan zorgen voor extra contrast, waardoor het menselijk lichaam duidelijker zichtbaar wordt. Om een goede MRI-scan te maken willen we alleen fotonen ontvangen afkomstig van een tweedimensionale “slice” van het menselijk lichaam. Dit wordt gedaan door de sterkte van het magneetveld te variëren langs het menselijk lichaam. Als gevolg krijgt elk deel van het menselijk lichaam ook zijn eigen resonantiefrequentie. Waterstofatomen zullen nu alleen aangeslagen worden op de plek waar de frequentie van de gebruikte fotonen (fMRI) gelijk is aan de resonantiefrequentie van het magneetveld (fr). In het onderstaande diagram zien we een horizontale stippellijn die overeenkomt met fMRI. Bij de rode grafiek is fMRI gelijk aan fr op een positie ter hoogte van de maag van het lichaam. Bij de oranje grafiek is het magneetveld versterkt, waardoor fMRI nu gelijk is aan fr ter hoogte van de ogen. Links zijn de bijbehorende foto’s te zien.
|
Bij echoscopie wordt ook gebruik gemaakt van de echo van geluidsgolven. Hieronder zien we bijvoorbeeld een echo van een foetus. Deze foto is gemaakt door korte ultrasone geluidspulsen de buik van een zwangere vrouw in te sturen. Een deel van deze geluidsgolven reflecteert op het moment dat een golf overgaat naar een materiaal met een andere geluidssnelheid. Doordat de golven vaak door meerdere lagen weefsel trekken, krijg je ook meerdere pulsen terug. Door te meten hoe lang het duurt voordat de verschillende pulsen terugkomen, kan een beeld gemaakt worden van de foetus.
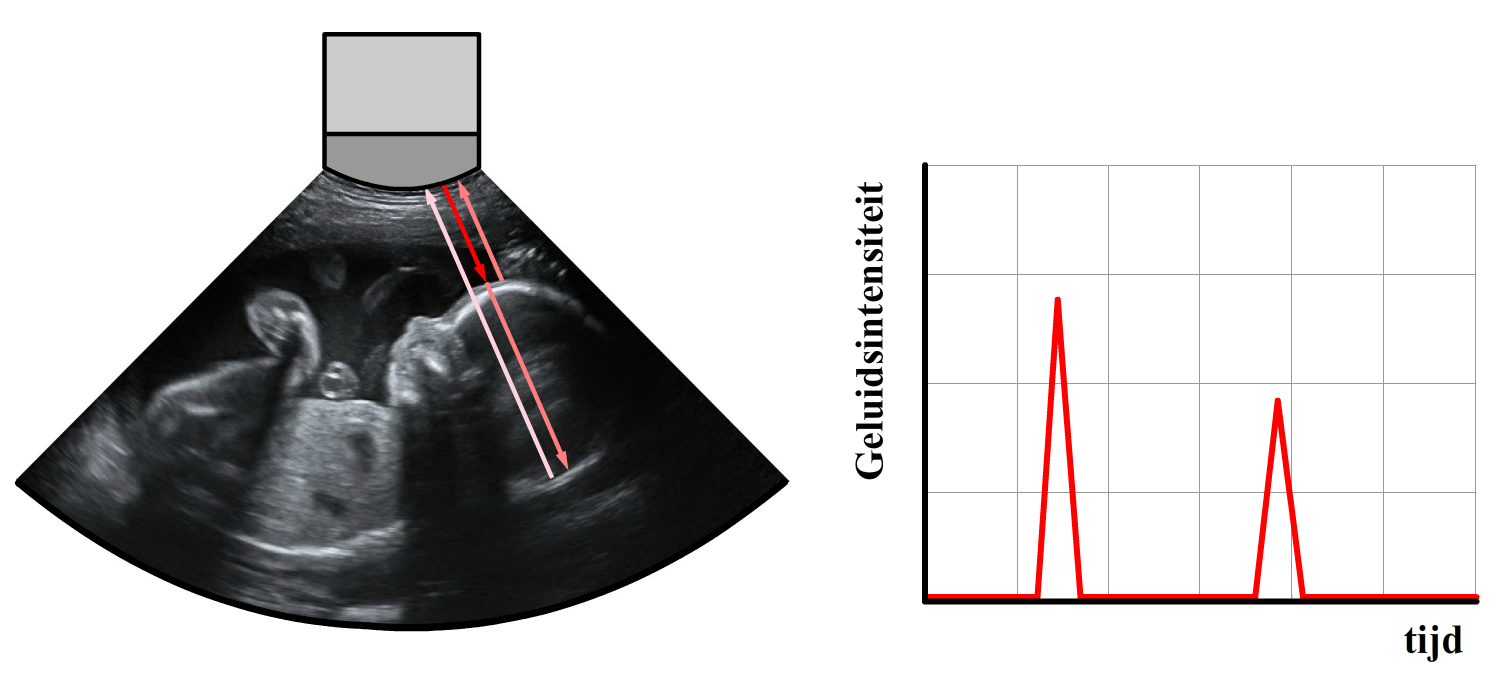
Voor het maken van een echo kan geen geluid gebruikt worden dat met het menselijk oor hoorbaar is. Hoorbaar geluid heeft namelijk een golflengte die veel groter is dan de details die we met een echo willen zien. Als gevolg buigen deze golven om deze details heen en kan er geen scherp beeld gemaakt worden. In plaats daarvan gebruiken we geluid met een frequentie hoger dan we met het oor kunnen waarnemen. We noemen dit ultrasoon geluid. Neem bijvoorbeeld een geluidsgolf van 5,0 MHz. Bij een temperatuur van ongeveer 40 graden Celsius is de geluidsnelheid in water gelijk aan 1529 m/s. De bijbehorende golflengte is dan:
$$\lambda = \frac{v}{f} \;\;\;\;\;\;\;\;\;\;\;\;\; \lambda = \frac{1529}{5,0 \times 10^6} = 0,30 \text{ mm}$$Met deze frequentie kunnen we dus details waarnemen tot ongeveer 0,30 mm groot. Dit levert het "pixel-achtige" beeld op dat in de bovenstaande afbeelding te zien is.
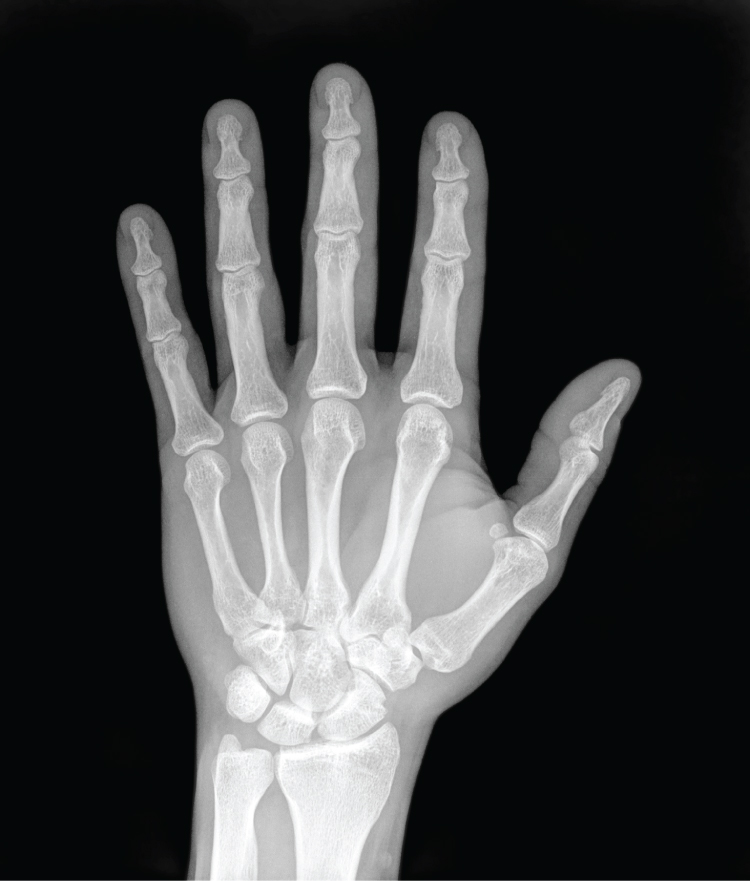
Een andere methode om het menselijk lichaam in kaart te brengen is de röntgenscan (zie de onderstaande linker afbeelding). Hierbij wordt röntgenstraling het lichaam in geschenen. Een deel van deze straling zal worden geabsorbeerd en de rest zal worden doorgelaten. Hoeveel er wordt geabsorbeerd hangt af van het soort stof waar de straling doorheen gaat en van de dikte van deze stof. Door de doorgelaten straling te detecteren, kan een röntgenfoto worden gemaakt. Doordat spierweefsel bijvoorbeeld meer röntgenstraling doorlaat dan bot, kunnen we de botten in het menselijk lichaam hiermee duidelijk in kaart brengen. Naast de tweedimensionale röntgenscans bestaan tegenwoordig ook driedimensionale versies. Dit worden CT-scans genoemd (zie de rechter afbeelding).
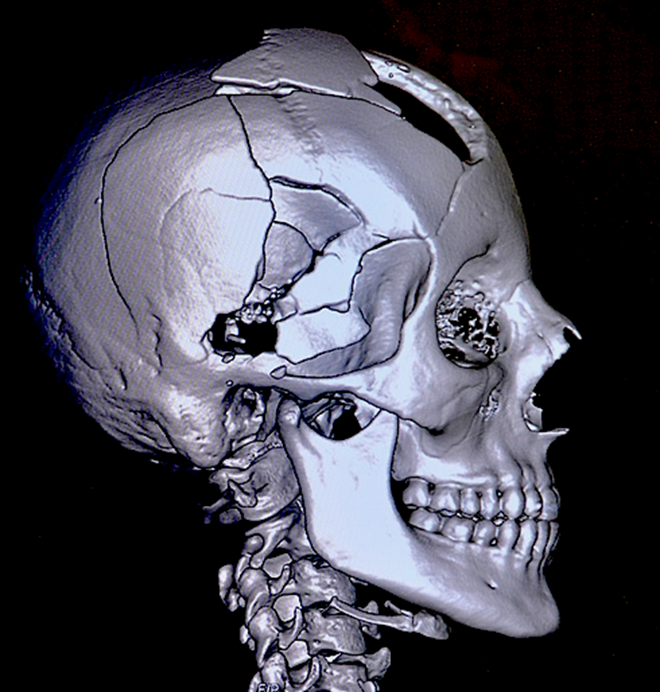 (Afbeelding: OpenStax; CC BY 4.0 / Michael Tsokos; GNU Free Documentation License, version 1.2)
(Afbeelding: OpenStax; CC BY 4.0 / Michael Tsokos; GNU Free Documentation License, version 1.2)
Hoeveel straling er wordt doorgelaten bij het maken van een röntgenfoto hangt af van de halveringsdikte van verschillende materialen. De halveringsdikte staat voor de afstand die straling kan afleggen door een materiaal totdat de helft van de straling geabsorbeerd is. De intensiteit van de straling neemt dus elke halveringsdikte met 50% af. In formuletaal wordt dit:
$$I_d = I_0 \left( \frac{1}{2} \right)^{n} \;\;\;\;\; \text{met:} \;\; n = \frac{d}{d_{1/2}} $$
|
De halveringsdikte hangt niet alleen af van het soort stof, maar ook van de energie van de straling. Een aantal halveringsdiktes zijn te vinden in BINAS voor verschillende hoeveelheden energie. Let erop dat de halveringsdikte hier wordt gemeten in centimeter.
In de formule staat ook de intensiteit. De eenheid van de intensiteit is joule per seconde per vierkante meter. Het vertelt ons hoeveel joule aan stralingsenergie er per seconde op een vierkante meter valt.
 VWO-STOF
VWO-STOF
| |||||||
|
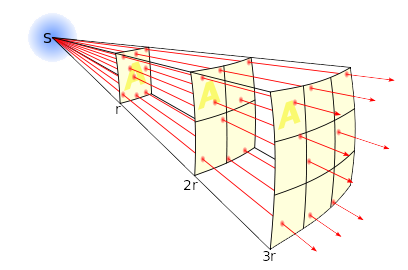
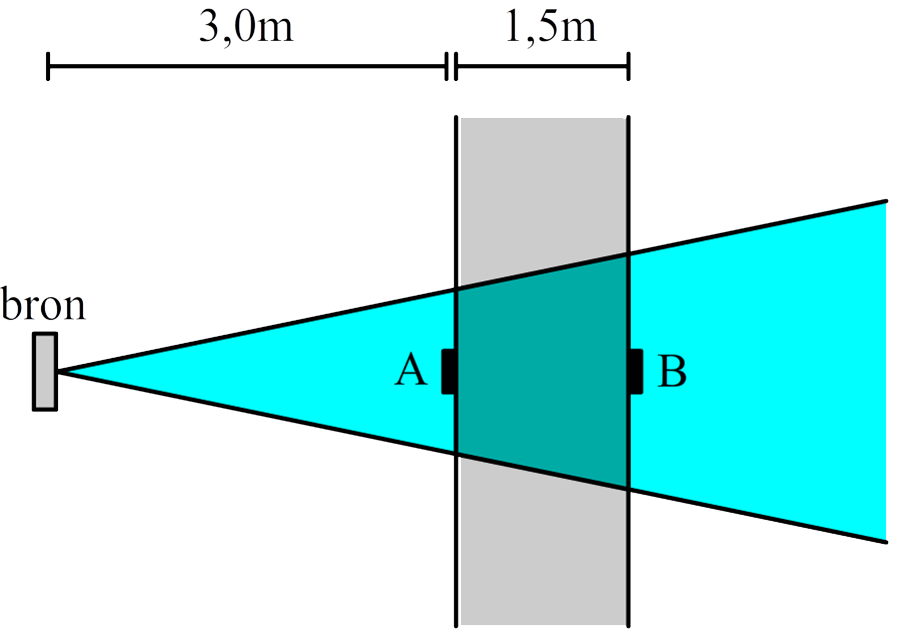
Als een bron straling uitzendt in alle richtingen, dan neemt de intensiteit van deze straling af met de afstand volgende zogenaamde kwadratenwet:
In de onderstaande afbeelding is goed te zien waarom de intensiteit van een divergerende bron afneemt met afstand. Hoe verder de straling komt, over hoe groter oppervlak de straling verdeeld wordt.
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
| BINAS: | |
| 5 | Elektronvolt |
| 7 | Massa van proton, neutron en elektron |
| 7 | Atomaire massa-eenheid (u) |
| 25 | Isotopen (halveringstijd, type straling en stralingsenergie per deeltje) |
| 27D2 | Stralingsnormen |
| 28F | Halveringsdiktes |
| 29 | Beknopte beschrijving methoden medische beeldvorming |