Hoofdstuk 1
Energie

§1 Soorten energie

In dit hoofdstuk gaan we leren de beweging van voorwerpen te beschrijven met behulp van het begrip energie. In de eerste paragraaf introduceren we een aantal soorten energie en de bijbehorende formules en gaan we het hebben over energieomzettingen.

Als we een stukje willen rennen, dan hebben we daar energie voor nodig. Als een vliegtuig opstijgt, dan is daar energie voor nodig. Als een lamp licht geeft, dan verbruikt deze lamp energie. Energie is overal om ons heen. Maar wat is energie eigenlijk? Als we zeggen dat een voorwerp energie heeft, dan kan dit twee dingen betekenen. Als een voorwerp beweegt, dan zeggen we dat het voorwerp kinetische energie (E_kin) heeft. Als het voorwerp de potentie heeft zichzelf of een ander voorwerp in beweging te brengen, dan zeggen we dat het voorwerp potentiële energie (E_pot) heeft.

De hoeveelheid kinetische energie die een bewegend voorwerp heeft, kunnen we berekenen met de volgende formule:

$$ E_{kin} = \frac{1}{2}mv^2 $$

Kinetische energie (E_kin)

joule (J)

Massa (m)

kilogram (kg)

Snelheid (v)

meter per seconde (m/s)

Zorg dat je alle grootheden in deze formule eerst omschrijft naar SI-eenheden. De massa moet dus gegeven worden in kilogram en de snelheid in meter per seconde. De SI-eenheid van de energie is de joule.

Een andere bekende soort energie is de zwaarte-energie. Als we een voorwerp optillen, dan heeft het de potentie om weer naar beneden te vallen. Daarom zeggen we dat elk voorwerp dat zich op een bepaalde hoogte bevindt, een hoeveelheid zwaarte-energie heeft. De hoeveelheid zwaarte-energie berekenen we als volgt:

$$ E_z = mgh $$

Zwaarte-energie (E_z)

joule (J)

Massa (m)

kilogram (kg)

Valversnelling (g)

meter per seconde per seconde (m/s²)

Hoogte (h)

meter (m)

Een andere bekende soort energie is de veerenergie. Dit is de energie die opgeslagen zit in een ingedrukte of uitgerekte veer. De veerenergie berekenen we als volgt:

$$ E_{veer} = \frac{1}{2}Cu^2 $$

Veerenergie (E_veer)

joule (J)

Veerconstante (C)

newton/meter (N/m)

Uitwijking (u)

meter (m)

Een andere energiesoort is de warmte (Q) die ontstaat door wrijving. Dat wrijving voor warmte zorgt kunnen we goed zien in de volgende afbeelding, gemaakt met een infrarood camera. We zien hier de warmte die ontstaat bij het remmen van een fiets.

De warmte die hierbij ontstaat, berekenen we als volgt:

$$ Q = F_w s $$

Warmte (Q)

joule (J)

Wrijvingskracht (F_w)

newton (N)

Afstand (s)

meter (m)

Er zijn nog vele andere soorten energie. Zo hebben we bijvoorbeeld de chemische energie (E_ch). Dit is de energie die is opgeslagen in de bindingen tussen atomen. Een bekend voorbeeld is de energie die in brandstoffen als benzine is opgeslagen. Chemische energie zit ook in bijvoorbeeld voedsel en batterijen. Daarnaast hebben we ook nog bijvoorbeeld elektrische energie (E_elek) en stralingsenergie (E_straling). Met stralingsenergie bedoelen we de energie in lichtdeeltjes. We voelen deze energie bijvoorbeeld als we in de zon lopen.

De verschillende soorten energie kunnen in elkaar worden omgezet. Neem bijvoorbeeld de verbranding van voedsel in het lichaam. Hier wordt de chemische energie uit voedsel omgezet in kinetische energie en warmte. Deze energieomzetting schrijven we als volgt op:

$$ E_{ch} \rightarrow E_{kin} + Q $$

Nog een voorbeeld. Als we een lampje aansluiten op een batterij, dan wordt chemische energie omgezet in elektrische energie en warmte. In de lamp wordt deze elektrische energie op zijn beurt weer omgezet in stralingsenergie en warmte. Deze energieomzettingen schrijven we als volgt op:

$$ E_{ch} \rightarrow E_{elek} + Q $$ $$ E_{elek} \rightarrow E_{straling} + Q $$

We kunnen energie dus omzetten van de ene naar de andere soort, maar de totale hoeveelheid energie blijft altijd gelijk. We noemen dit de wet van behoud van energie. In wiskundige termen kunnen we deze wet opschrijven als:

$$ E_{tot,b} = E_{tot,e} $$

Totale energie aan het begin (E_tot,b)

joule (J)

Totale energie aan het eind (E_tot,e)

joule (J)

Laten we een voorbeeld bespreken waarbij we de wet van behoud van energie toepassen. Een kanonskogel met onbekende massa wordt onder een willekeurige hoek afgeschoten van de top van een kasteel op een hoogte van 30 m. De beginsnelheid van de kogel is 20 m/s. Bereken de snelheid waarmee de kogel tegen de grond komt. We verwaarlozen de wrijvingskracht.

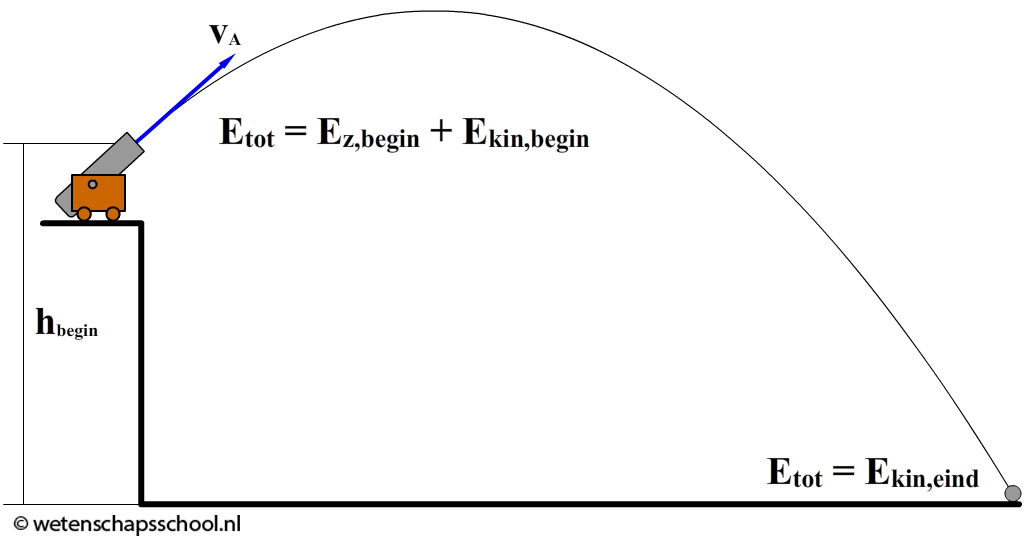
Op het moment dat de kogel wordt afgeschoten heeft de kogel zowel kinetische energie als zwaarte-energie. Als de kogel neerkomt, is er geen zwaarte-energie meer. Er geldt dus:

$$ E_{tot,b} = E_{tot,e} $$ $$ E_{kin,b} + E_{z,b} = E_{kin,e} $$ $$ \frac{1}{2}mv_{b}^2 + mgh = \frac{1}{2}mv_{e}^2 $$

Alle termen bevatten een m, dus kunnen we deze wegdelen:

$$ \frac{1}{2}v_{b}^2 + gh = \frac{1}{2}v_{e}^2 $$ $$ \frac{1}{2}\times 20^2 + 9,81 \times 30 = \frac{1}{2}v_{e}^2 $$ $$ 495 = \frac{1}{2}v_{e}^2 $$ $$ v_{e} = \sqrt{989} = 31 \text{ m/s} $$

Merk op hoe krachtig deze methode is! Met deze formule hebben we de eindsnelheid van de kogel berekend, zonder de massa van de kogel te weten of de hoek waaronder de kogel is afgeschoten.

Laten we nu een aantal voorbeelden bespreken waarbij de wrijvingskracht wel een rol speelt. Neem bijvoorbeeld een fietser die op zijn rem trapt totdat hij stilstaat. In de beginsituatie had de fietser kinetische energie. Aan het eind van de beweging is deze energie omgezet in warmte. Er geldt dus:

$$ E_{tot,b} = E_{tot,e} $$ $$ E_{kin,b} = Q $$

Als we dit uitschrijven, dan vinden we:

$$ \frac{1}{2}mv^2 = F_{w} s $$

Met deze formule kunnen we o.a. de wrijvingskracht bepalen die de fiets ondervindt.

Nog een voorbeeld. Een bal wordt tegen een helling op gerold. Op het hoogste punt staat de bal even stil en is er dus geen kinetische energie meer. Er is hier wel zwaarte-energie. Er geldt dus:

$$ E_{tot,b} = E_{tot,e} $$ $$ E_{kin,b} = E_{z,e} + Q $$

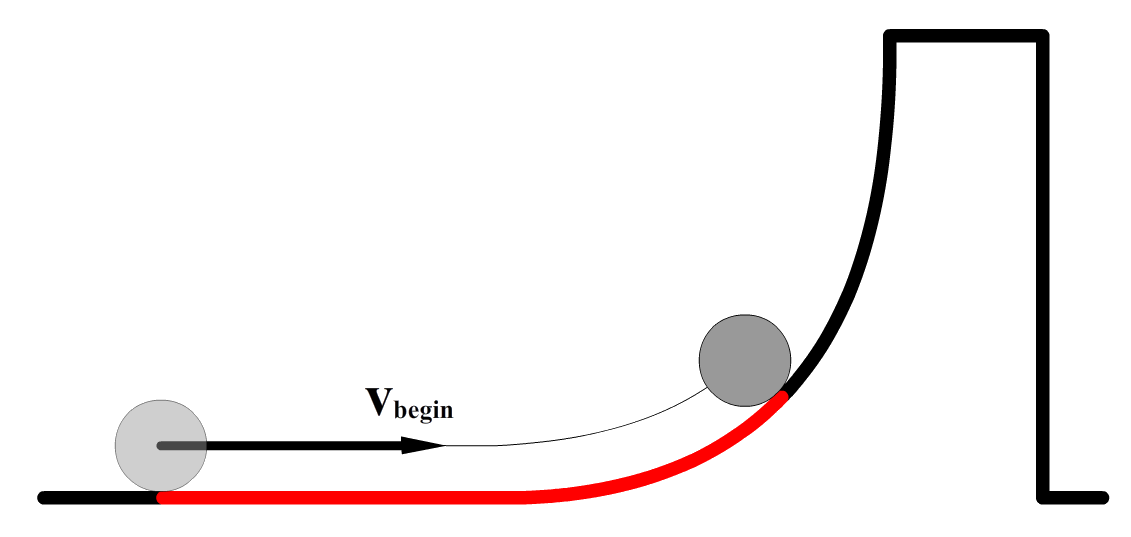
Met deze formule kunnen we bijvoorbeeld uitrekenen hoeveel warmte er bij het rollen is ontstaan.

Energieomzettingen beschrijven

(4p) Hieronder zien we een luchtballon, zonnecellen, een föhn en een dynamo afgebeeld. Beschrijf de energieomzettingen die hier plaatsvinden.

(2p) In welke twee energiesoorten wordt de chemische energie in voedsel omgezet?

(1p) Een kogel valt van de toren van Pisa. Welke energieomzetting vindt er tijdens het vallen plaats?

(2p) Een bal wordt verticaal afgeschoten met behulp van een veer. Welke energieomzetting vindt plaatst vanaf het begin van de beweging totdat de bal zijn hoogste punt bereikt heeft?

(3p) Op een marineschip wordt elektriciteit opgewekt met een dieselmotor. Deze motor verbrandt stookolie en zet hiermee een generator in beweging, die elektriciteit produceert. In de onderstaande afbeelding zijn deze twee processen met pijlen op schaal weergegeven.

Noteer bij elke pijl de juiste energie. Kies uit kinetische energie, chemische energie, elektrische energie en warmte. Sommige soorten energie zullen meerdere keren voorkomen.
(bron: examen 2019-1 HAVO)

Werken met de wet van behoud van energie

(1p) Laat met behulp van de formule voor de kinetische energie zien wat de eenheid van joule is in SI-grondeenheden.

(4p) Laat ook zien dat je hetzelfde antwoord vindt als je de formule voor de zwaarte-energie, de veerenergie en de warmte gebruikt.

Beschrijf in de volgende situaties de energie-omzetting:

(1p) Een kogel wordt vanuit stilstand over een horizontaal oppervlak afgeschoten met behulp van een veer. De kogel verlaat de veer met een bepaalde snelheid. De wrijvingskracht is te verwaarlozen.

(1p) Een bal rolt met een beginsnelheid een helling op. Na een tijdje behaalt de bal zijn hoogste punt. De wrijvingskracht mag worden verwaarloosd.

(1p) Een bal wordt vanuit stilstand omhoog geschoten met behulp van drie veren. Na een bepaalde tijd bereikt de bal zijn hoogste punt.

(1p) Een blok wordt boven een grote veer losgelaten. Door de zwaartekracht van het blok drukt de veer in. Op een gegeven moment is de veer maximaal ingedrukt. De wrijvingskracht is te verwaarlozen.

(1p) Een persoon wordt met behulp van een bungee-elastiek een hoogte h opgetild met behulp van een elektromotor. Tijdens het optillen rekken de elastieken een uitwijking u uit. Wrijvingskracht is te verwaarlozen.

(1p) Een bal wordt van een helling afgerold met een snelheid van 30 m/s. Even later is de snelheid toegenomen.

(3p) Een baksteen valt van een hoogte van 10 meter naar beneden. De wrijvingskracht is te verwaar-lozen. Bereken de snelheid waarmee de steen tegen de grond aan komt.

(4p) Een bal met een massa van 350 gram rolt vanuit stilstand van een helling. De helling heeft een lengte van 10 meter en een hoogte van 6,4 m. De snelheid van de bal aan het eind van de helling is 10 m/s. Bereken de hoeveelheid energie die is omgezet in warmte.

(4p) Een persoon gooit een honkbal met een snelheid van 45 km/h weg. Hij laat de honkbal los op een hoogte van 1,80 meter. Bereken de snelheid waarmee de honkbal tegen de grond komt. Verwaarloos de wrijvingskracht.

(4p) Een persoon heeft een slinger aan een statief gemonteerd. De slinger bestaat uit een koord met daaraan een massa. De massa wordt uit zijn evenwichtsstand getrokken, totdat de hoogte 5,0 cm is toegenomen. Bereken de maximum snelheid die de massa zal ondervinden bij het heen en weer slingeren. Je mag de wrijvingskracht verwaarlozen.

(5p) In de onderstaande afbeelding zien we een persoon die een sprong maakt met powerskips. Maak een schatting van de veerenergie die nodig was voor deze sprong.

Hieronder zien we het (v,t)-diagram van een remmende motorfiets. De motorfiets met passagier heeft een totale massa van 270 kg.

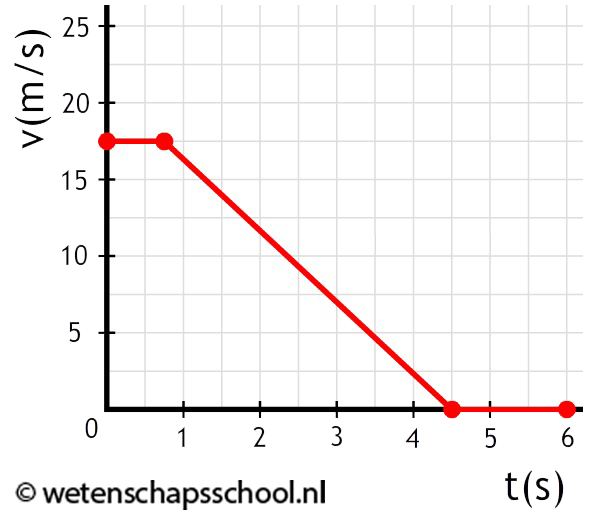
(4p) Laat met behulp van het diagram zien dat de warmte die tijdens het remmen ontstaat gelijk is aan 4,1 x 10⁴ J.

(3p) Bepaal de wrijvingskracht werkende op de motorfiets tijdens het remmen.

In de onderstaande afbeelding zien we een deel van een achtbaan schematisch afgebeeld. Deze figuur is niet op schaal. De helling AB maakt een hoek van 25 graden met het horizontale vlak. Het hoogteverschil tussen A en B bedraagt 29 m. De trein heeft zelf geen motor maar wordt met behulp van een ketting in 33 s met een constante snelheid omhoog getrokken over de helling AB.

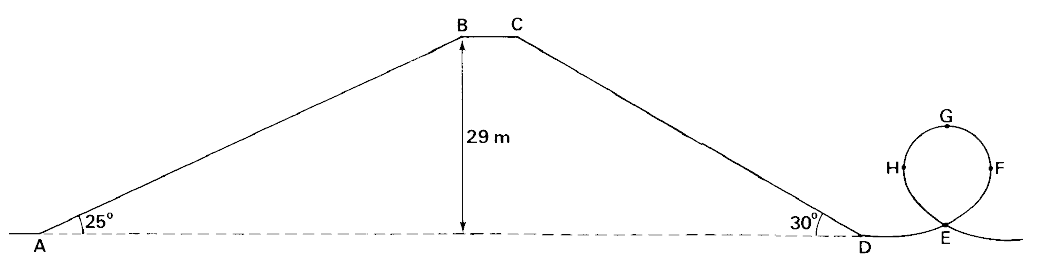
(3p) Bereken de snelheid van de trein op het traject AB.

(4p) De energie die nodig is om de trein van A naar B te trekken wordt geleverd door een elektromotor die is aangesloten op een spanning van 380 V. De totale massa van de trein met passagiers bedraagt 6,65 x 10³ kg. Bereken de stroomsterkte die de spanningsbron moet leveren als er geen wrijvingskracht zou werken. Je mag aannemen dat de snelheid gedurende het hele traject hetzelfde is gebleven.

(3p) De trein daalt daarna met een verwaarloosbare beginsnelheid af van punt C naar punt D. Punt G bevindt zich 15 meter boven punt D. Ga na met welke snelheid punt G bereikt wordt. Verwaarloos de wrijvingskracht.

(3p) In werkelijkheid werkt er natuurlijk wel een wrijvingskracht op het traject. Tussen punt C en D is deze kracht gelijk aan 2,50 x 10³ N. De hellingshoek op dit traject is 30 graden. Bereken met deze informatie de warmte die op traject CD is ontstaan.

(bron: examen VWO 1990-2)

(5p) Een leerling gaat trampolinespringen op een bungee-trampoline. Ze krijgt een tuigje om, waaraan twee elastische koorden zijn vastgemaakt. De elastische koorden zitten vast aan staalkabels. Deze kabels worden door een elektromotor om een haspel gewonden. Hierdoor wordt de leerling langzaam verticaal omhooggetrokken, totdat ze een flink stuk boven de trampoline stil hangt.
Vervolgens wordt de leerling door een helper omlaag getrokken totdat haar voeten de trampoline raken en zij zich kan afzetten. In het onderstaande (v,t)-diagram is de beweging van het zwaartepunt van de leerling weergegeven tijdens een aantal sprongen. In het diagram zien we de verandering van verschillende soorten energie in de tijd. Geef aan welke grafiek overeenkomt met de kinetische energie, welke met de zwaarte-energie, welke met de veerenergie van de elastieken, welke met de veerenergie van de trampoline en welke met de totale energie.

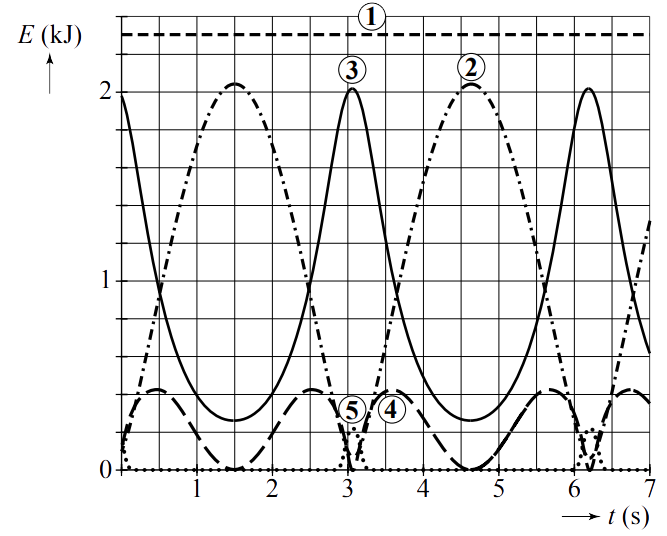
(bron: examen VWO 2011-1)

(4p) In de onderstaande afbeelding is een bal afgebeeld die naar de grond valt van de eerste verdieping van een gebouw. Bereken op twee manieren wat de snelheid is waarmee de bal tegen de grond botst. Gebruik eerst de hoogte vanaf de grond op de eerste verdieping en gebruik daarna de hoogte vanaf de begane grond. Laat zien dat je in beide gevallen hetzelfde antwoord vindt. Je mag de wrijvingskracht verwaarlozen.

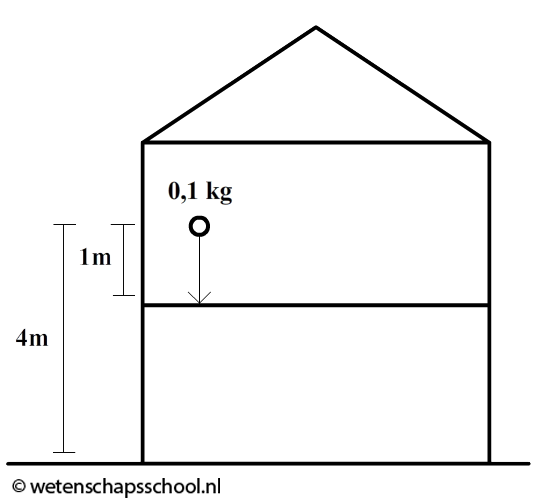
(VWO) In de rechter afbeelding is het (v,t)-diagram van een vallend voorwerp weergegeven.

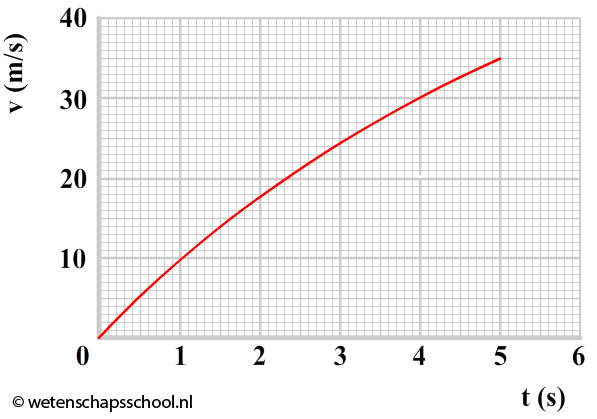
(1p) Hoe zie je aan de grafiek dat het voorwerp luchtwrijving ondervindt?

(6p) Bepaal hoeveel procent van de oorspronkelijke zwaarte-energie in warmte is omgezet ten gevolge van de luchtweerstand.

§2 Chemische energie

In de eerste paragraaf hebben we het even gehad over chemische energie. Dit is de energie die is opgeslagen in de bindingen tussen atomen. Een bekend voorbeeld is de energie in brandstoffen zoals benzine. In deze paragraaf gaan we met deze energie leren rekenen.

In verbrandingsmotoren wordt de chemische energie in brandstof omgezet in beweging. Niet al deze chemische energie zal echter nuttig gebruikt worden. De energie die wel nuttig gebruikt wordt, noemen we de motorenergie (E_motor). De rest van de energie gaat verloren in de vorm van warmte (Q_motor). Er geldt dus:

$$ E_{ch} = E_{m} + Q_{m} $$

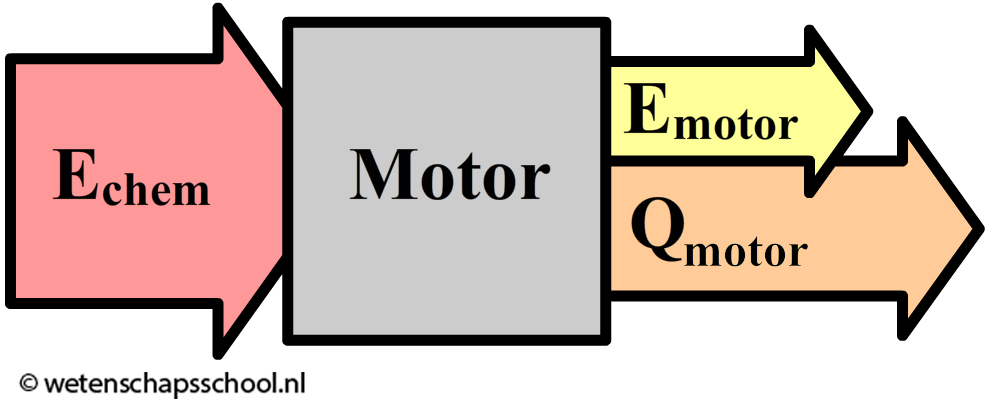
De fractie van de energie die nuttig gebruikt wordt noemen we het rendement:

$$ \frac{E_{nuttig}}{E_{totaal}} = \eta $$

Nuttige energie (E_nuttig)

joule (J)

Totale energie (E_totaal)

joule (J)

Rendement (η)

-

Voor een verbrandingsmotor wordt dit:

$$ \frac{E_{m}}{E_{ch}} = \eta $$

Motorenergie (E_m)

joule (J)

Chemische energie (E_ch)

joule (J)

Rendement (η)

-

Het rendement is in deze formule een getal tussen de 0 en de 1. Het rendement wordt ook vaak uitgedrukt als percentage. In dat geval moet het rendement uit de formule vermenigvuldigd worden met 100. Als η gelijk is aan 0,20, dan is het rendement dus 20%.

We kunnen de motorenergie ook uitrekenen met de volgende formule:

$$ E_{motor} = F_{motor} s $$

Motorenergie (E_motor)

joule (J)

Motorkracht (F_motor)

newton (N)

Afstand (s)

meter (m)

De chemische energie berekenen we met de stookwaarde. De stookwaarde vertelt ons hoeveel joule aan chemische energie er in een kubieke meter van een bepaalde brandstof zit. Benzine heeft bijvoorbeeld een stookwaarde van 33 × 10⁹Jm^-3. Dit betekent dus dat je uit een kubieke meter benzine 33 × 10⁹ joule aan chemische energie kan halen. Voor een heel aantal brandstoffen kan je de stookwaarde in BINAS opzoeken. Met de stookwaarde kunnen we als volgt de hoeveelheid chemische energie berekenen:

$$ E_{ch} = r_v V$$

Chemische energie (E_ch)

joule (J)

Stookwaarde (r_v)

joule per kubieke meter (J/m³)

Volume (V)

kubieke meter (m³)

Stel we willen bijvoorbeeld weten hoeveel chemische energie er in 3,0 liter benzine zit. We berekenen dit als volgt:

$$ V = 3,0 \text{ L} = 3,0 \text{ dm}^3 = 3,0 \times 10^{-3} \text{ m}^3 $$ $$ E_{ch} = r_v V $$ $$ E_{ch} = 33 \times 10^9 \times 3,0 \times 10^{-3} = 9,9 \times 10^7 \text{ J} $$

Voorbeeld

Opdracht:

Een verbrandingsmotor levert 10 × 10⁷ J aan nuttige energie en heeft een rendement van 30%. Bereken hoeveel liter benzine hiervoor moet worden verbrand.

Antwoord:

We beginnen met de formule voor rendement:
$$ \frac{E_m}{E_{ch}} = \eta $$
Hiermee berekenen we de chemische energie:
$$ E_{ch} = \frac{E_m}{\eta} = \frac{10 \times 10^7}{0,30} = 3,3 \times 10^{8} \text{ J} $$
Met de chemische energie berekenen we het volume. We zoeken hiervoor eerst de stookwaarde op van benzine. Volgens BINAS geldt r_V = 33 × 10⁹ J/m³.
$$ V = \frac{E_{ch}}{r_V} = \frac{3,3 \times 10^{8} }{33\times 10^9} = 0,010 \text{ m}^3 = 10 \text{ L}$$
Er is dus 10 L benzine verbrand.

Rekenen met de chemische energie, de motorenergie en het rendement

Beschrijf in de volgende situaties de energieomzetting:

(1p) Benzine wordt verbrand in de motor van een auto.

(1p) Een auto versnelt vanuit stilstand over een horizontale weg en behaalt na een bepaalde tijd een bepaalde snelheid.

(1p) Een auto rijdt met een snelheid van 70 km/h tegen een helling op. Na een afstand s is de snelheid afgenomen tot 30 km/h.

(2p) Een auto rijdt met een constante snelheid tegen een helling op.

(4p) Een tractor verbrandt tijdens een rit 250 mL aan benzine. Bereken hoeveel chemische energie de tractor verbrand heeft.

(3p) Een auto verbruikt 3,0 x 10⁴ J aan motorenergie. De auto heeft een rendement van 40%. Bereken hoeveel milliliter benzine de auto verbrandt.

In een dieselmotor met een rendement van 33% wordt 0,50 L gasolie verbrand.

(5p) Bereken hoeveel energie de motor hierbij nuttig verbruikt.

(2p) De motorkracht van de auto is 2,8 x 10³ N. Bereken de afstand die de auto hiermee kan afleggen.

(6p) Een auto met een rendement van 45% verbrandt 1,5 L benzine in 15 kilometer. Bereken de motorkracht van de auto.

Een auto maakt een rit met een constante snelheid waarbij 4,5 L aan benzine verbrand wordt. Het rendement van de motor is 45%. De motorkracht waarmee de auto voortbeweegt is 3,2 × 10³ N.

(4p) Bereken hoeveel warmte er in de motor is ontstaan tijdens deze beweging.

(2p) Bereken hoeveel warmte er is ontstaan door de wrijving tussen de wielen en de weg.

(4p) Bereken de afstand die de auto heeft afgelegd.

(5p) Een auto met een massa van 4,0 × 10³ kg rijdt vanuit stilstand tegen een helling op met een hellingshoek van 10 graden. De auto begint op een hoogte van 30 meter en eindigt met een snelheid van 28,8 km/h op een hoogte van 45 meter. De motorkracht van de auto tijdens de rit is 1,5 × 10³ N. Bereken de gemiddelde wrijvingskracht die de auto ondervindt.

(VWO, 5p) Vergelijk de chemische energie in een kubieke meter benzine en een kubieke meter balsahout.

§3 Arbeid

In deze paragraaf gaan we begrijpen waar de energieformules uit de vorige paragrafen vandaan komen. We hebben hiervoor het begrip arbeid nodig.

Om te begrijpen waar het begrip energie vandaan komt, moeten we eerst het begrip arbeid (W) bestuderen. Als er een kracht F op het voorwerp werkt en dit voorwerp een afstand s verplaatst, dan zeggen we dat deze kracht een arbeid uitoefent op het voorwerp. De arbeid wordt gegeven door:

$$W = F_{gem}s\cos{\alpha}$$

Arbeid (W)

joule (J)

Kracht (F)

newton (N)

Afgelegde weg (s)

meter (m)

Hoek tussen kracht en bewegingsrichting (α)

graden (^o)

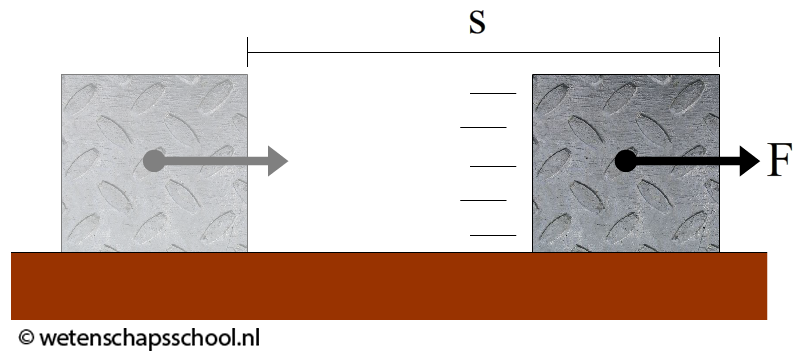
Laten we als voorbeeld even kijken naar de bovenstaande afbeelding. Een blok wordt met een spierkracht naar rechts geduwd. De spierkracht wijst hier in de bewegingsrichting. De hoek tussen de kracht en de bewegingsrichting is dus gelijk aan 0° en cos 0° = 1. De formule versimpelt in dit geval dus tot:

$$W_{spier} = F_{spier}s \cos{0^\circ} = F_{spier}s$$

Behalve de spierkracht werkt er in het bovenstaande voorbeeld ook een wrijvingskracht. De wrijvingskracht werkt tegen de bewegingsrichting in. De hoek tussen de bewegingsrichting en de wrijvingskracht is hier dus 180° en cos 180° = -1. Er geldt dus:

$$ W_w = F_ws \cos{180^{\circ}} = -F_ws $$

De wrijvingskracht oefent dus een negatieve arbeid uit op het voorwerp.

In de bovenstaande afbeelding werken ook de normaalkracht en de zwaartekracht. Deze krachten staan loodrecht op de bewegingsrichting. De hoek tussen de kracht en de bewegingsrichting is in dit geval dus 90° en cos 90° = 0. Deze krachten oefenen dus geen arbeid uit op het voorwerp:

$$ W_z = F_zs \cos{90^\circ} = 0 $$ $$ W_n = F_ws \cos{90^\circ} = 0 $$

Laten we deze formule eens toepassen op een voorwerp dat van hoogte h naar de grond valt. We verwaarlozen de wrijvingskracht. We vinden dan:

$$ W_z = F_zs\cos{0^\circ} = F_zs = mgh = E_z$$

We hebben hier dus gevonden dat de arbeid die de zwaartekracht verricht gelijk is aan de zwaarte-energie:

$$ W_z = E_z$$

Op eenzelfde manier kunnen we ook de formules voor de andere energiesoorten afleiden.

Op de website leiden we ook af dat in alle omstandigheden het zogenaamde arbeid-energie theoremageldt:

In de onderstaande extra theorie leiden we ook af dat in alle omstandigheden het zogenaamde arbeid-energie theoremageldt:

$$\Sigma W = \Delta E_{kin}$$

De som van de arbeid (ΣW)

joule (J)

De toename van de kinetische energie (E_kin)

joule (J)

Extra

Als we alle arbeiden die op een voorwerp werken bij elkaar optellen dan vinden we:
$$ \Sigma W = F_1s + F_2s + ... = (F_1 + F_2 + ...)s $$
Aan de rechter zijde zien we tussen haakjes alle krachten bij elkaar opgeteld. Dit is gelijk aan de resulterende kracht. Er geldt dus:
$$ \Sigma W = F_{res}s $$
In plaats van de afgelegde weg (s), kunnen we ook de verplaatsing (Δx) opschrijven:
$$ \Sigma W = F_{res}\Delta x $$
Met de tweede wet van Newton kunnen we dit uitschrijven tot:
$$ \Sigma W = ma\Delta x $$
Met Δv/Δt = a, vinden we dan:
$$ \Sigma W = m\frac{\Delta v}{\Delta t}\Delta x = m \Delta v \frac{\Delta x}{\Delta t} $$
Omdat Δx/Δt = v_gem, kunnen we dit schrijven als:
$$ \Sigma W = m\Delta v v_{gem} $$
Dit kunnen we verder uitschrijven met behulp van:
$$ \Delta v = v_{eind} - v_{begin} $$ $$ v_{gem} = \frac{v_{eind} + v_{begin}}{2} $$
Als de deze formules invullen en netjes alle haakjes wegwerken, dan vinden we:
$$ \Sigma W = \frac{1}{2}mv^2_{eind} - \frac{1}{2}mv^2_{begin} $$
We vinden hiermee dus het arbeid-energie theorema:
$$ \Sigma W = \Delta E_{kin} $$

Laten we deze formule eens invullen voor het geval van een voorwerp dat valt vanaf hoogte h. We verwaarlozen de wrijvingskracht. In dat geval oefent alleen de zwaartekracht een arbeid uit en is de kinetische energie aan het begin nul. We vinden dan:

$$ W_z = E_{kin,e}$$ $$E_{z,b} = E_{kin,e}$$

We hebben hier afgeleid dat de arbeid van de zwaartekracht ervoor zorgt dat zwaarte-energie wordt omgezet in kinetische energie. Dit is precies de energieomzetting die we hadden verwacht bij een vallend voorwerp!

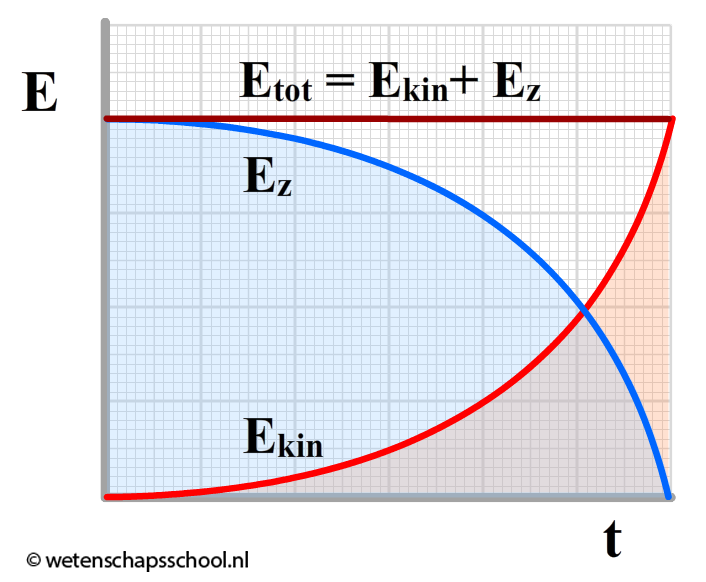
In het onderstaande diagram is de omzetting schematisch weergegeven. Merk op dat als de zwaarte-energie afneemt, de kinetische energie evenveel toeneemt. Als we beide grafieken bij elkaar optellen, dan zien we dat de totale energie behouden is.

Rekenen met arbeid en het arbeid-energietheorema

(1p) Leg uit hoe de hoek α gedefinieerd is.

Een persoon duwt met een spierkracht van 200 N tegen een blok met een onbekende massa. Het blok beweegt hierdoor met constante snelheid van 3,0 m/s naar rechts.

(3p) Bereken de arbeid die de spierkracht per seconde verricht heeft.

(4p) Bereken de arbeid die de wrijvingskracht verricht heeft.

(3p) Bereken de arbeid die de zwaartekracht en de normaalkracht verricht hebben.

(1p) Een persoon heeft een zak zand van 25 kg stil in zijn handen. Bereken de arbeid die de zwaartekracht verricht op de zak.

Een persoon gooit een steen met een massa van 3,5 kg recht omhoog. De steen legt 4,5 meter af omhoog en legt daarna dezelfde afstand weer af naar beneden. De gemiddelde wrijvingskracht die op de steen werkt is zowel bij het omhoog als bij het omlaag bewegen gelijk aan 8,5 N.

(4p) Bereken de arbeid die de zwaartekracht en de wrijvingskracht verricht hebben terwijl de steen omhoog bewoog.

(4p) Bereken de totale arbeid die op de steen werkt terwijl deze omhoog beweegt. Is de totale arbeid nul, positief of negatief? Leg aan de hand van het arbeid-energietheorema uit waarom je dit verwacht had.

(4p) Bereken de arbeid die de zwaartekracht en de wrijvingskracht verricht hebben terwijl de steen naar beneden bewoog.

(4p) Bereken de totale arbeid die op de steen werkt terwijl deze omlaag beweegt. Is de totale arbeid nul, positief of negatief? Leg aan de hand van het arbeid-energietheorema uit waarom je dit verwacht had.

(2p) Een goede kogelstoter wil tijdens het stoten over een zo lang mogelijke afstand contact houden met de kogel. Leg uit waarom dit een goede strategie is. Gebruik in je antwoord de begrippen verplaatsing, arbeid en het arbeid-energietheorema.

Bij veel auto's blaast bij een botsing automatisch een airbag op. Hierdoor wordt vaak letsel voorkomen.

(2p) Leg uit hoe een airbag werkt. Gebruik in je antwoord de begrippen arbeid-energietheorema, arbeid en verplaatsing.

(4p) Een persoon met een massa van 70 kg komt met een snelheid 30 m/s tegen een airbag. De airbag deukt hierdoor 20 cm in. Je mag aannemen dat bij de airbag geen vering optreedt. Bereken de kracht die tijdens de botsing op deze persoon werkt met behulp van het arbeid-energietheorema.

(3p) Vind wederom de kracht die tijdens de botsing op deze persoon werkt, maar nu met behulp van de wet van behoud van energie.

(VWO) Een steen wordt met een constante snelheid rondgeslingerd aan een touw.

(2p) Bereken de arbeid die de middelpuntzoekende kracht verricht.

(1p) Leg aan de hand van het arbeid-energietheorema uit waarom je dit antwoord had kunnen verwachten.

(3p) Een leerling met een massa van 48 kg laat zich wegschieten met een grote katapult. Hij neemt plaats op een zitje dat is verbonden aan twee elastische koorden met elk een veerconstante van 600 N/m. Dan wordt de leerling 3,0 meter naar beneden getrokken met behulp van een elektromotor. De elastieken rekken hierdoor 4,5 m uit. Bereken de arbeid die de elektromotor minimaal moet verrichten om de leerling op deze positie te krijgen. Je hoeft geen rekening te houden met de uitrekking van de elastieken die wordt veroorzaakt door de massa van de leerling.

(VWO) Een voorwerp met een massa van 20 kg glijdt met een versnelling van 0,50 m/s² van een helling af met een hellingshoek van 29 graden. Het voorwerp begint zijn beweging bovenaan de helling op een hoogte van 7,5 meter.

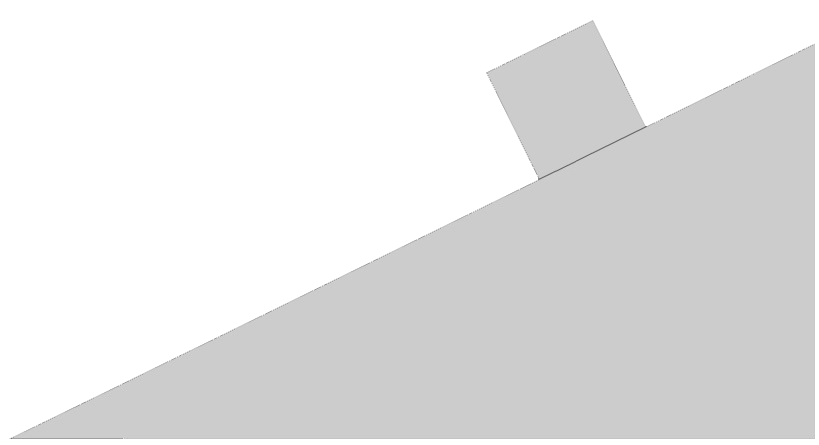
(2p) Bereken de arbeid die de normaalkracht verricht heeft.

(4p) Bepaal de arbeid die de zwaartekracht verricht heeft met de formule uit deze paragraaf.

(3p) Bereken de arbeid die de zwaartekracht verricht heeft met behulp van de zwaarte-energie en laat zien dat je hetzelfde antwoord vindt.

§4 Vermogen

In deze paragraaf introduceren we verschillende formules voor het vermogen.

Het vermogen (P) wordt gemeten in watt (W) en dit is gelijk aan joule per seconde. We kunnen het vermogen op de volgende twee manieren berekenen:

$$P = \frac{W}{\Delta t} = \frac{\Delta E}{\Delta t}$$

Vermogen (P)

watt (W)

Toename van de energie (ΔE)

joule (J)

Arbeid (W)

joule (J)

Tijdsduur (Δt)

seconde (s)

De formule P = W/Δt kunnen we ook herschrijven met behulp van W = FΔx. We vinden dan:

$$P = \frac{F\Delta x}{\Delta t} = Fv$$

We kunnen het vermogen dus ook bereken met:

$$P = Fv$$

Vermogen (P)

watt (W)

Kracht (F)

newton (N)

Snelheid (v)

meter per seconde (m/s)

Voorbeeld

Vraag:

Een sprinter met een massa van 80 kg bereikt binnen 2,0 seconden een snelheid van 10 m/s. Bereken het gemiddelde vermogen dat hier minimaal voor nodig is.

Antwoord:

Het minimale vermogen is het vermogen zonder verlies door warmte. We zijn hier dus alleen geïnteresseerd in de kinetische energie die is ontstaan. We vinden:
$$ E_{kin} = \frac{1}{2}\times 10 \times 10^2 = 5,0\times 10^2 \text{ J}$$
Het vermogen wordt dan dus:
$$P = \frac{\Delta E}{\Delta t} = \frac{5,0 \times 10^2}{2} = 2,5 \times 10^2 \text{ W}$$
Er is dus minimaal gemiddeld 2,5 × 10² joule per seconde omgezet in kinetische energie.

Redeneren met energie en vermogen

(4p) Een auto heeft een topsnelheid van 230 km/h. Het maximale vermogen van de motor van de auto is 105 kW. Bereken de grootte van de totale wrijvingskracht werkend op de auto bij deze snelheid.

(1p) Een auto versnelt vanuit stilstand met een constant vermogen. Leg uit of de motorkracht tijdens deze beweging gelijk blijft, groter wordt of kleiner wordt.

Een leerling stapt in een attractie bestaande uit een hoge mast met een zweefmolen. Nadat de passagiers in de stoeltjes hebben plaatsgenomen, beweegt de zweefmolen eerst zonder te draaien langs de mast omhoog. In 8,0 s gaat de zweefmolen 30 meter omhoog. In de mast bevindt zich een contragewicht met een massa gelijk aan de totale massa van de zweefmolen zonder passagiers. Dit contragewicht is via een katrol boven in de mast verbonden met de zweefmolen en daalt met dezelfde snelheid als de verticale snelheid van de zweefmolen. Zo wordt energie bespaard. Voor de verticale verplaatsing wordt een elektromotor gebruikt met een rendement van 90%. Neem aan dat er 22 passagiers met een gemiddelde massa van 60 kg in de stoeltjes hebben plaatsgenomen.

(6p) Bereken het minimale elektrische vermogen van deze elektromotor.

(1p) Na het omhooggaan begint de zweefmolen te draaien. Hiervoor wordt een tweede elektromotor gebruikt. Op t = 0 s begint de zweefmolen te draaien en na 5 s draait hij met constante snelheid. Het vermogen van deze tweede elektromotor is in de onderstaande afbeelding uitgezet tegen de tijd:
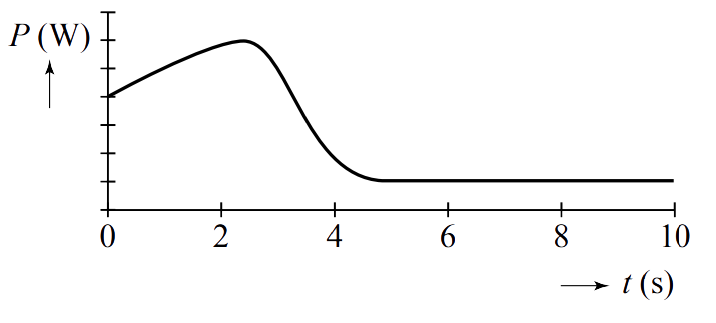
Waarom is het vermogen voor t = 5 s groter dan na t = 5 s?

(1p) Waarom is het vermogen na t = 5 s niet gelijk aan 0 W?

(bron: examen VWO 2012-1)

De Kingda Ka is één van de snelste en hoogste achtbanen ter wereld. Wie in de Kingda Ka stapt, maakt mee dat de trein in 3,5 seconde vanuit stilstand tot 205 km/h wordt versneld en daarna 139 m omhoog wordt gejaagd. Vervolgens stort de trein zich loodrecht in de diepte, waarna een tweede heuvel volgt. Bij de start wordt de trein van de Kingda Ka op een horizontale baan versneld. Een elektromotor zorgt hier voor de aandrijving. De massa van de trein met passagiers bedraagt 3,3 × 10³ kg.

(4p) Bepaal het gemiddelde vermogen dat de elektromotor gedurende de eerste 3,5 s minimaal moet leveren.

(1p) Waarom gebruiken we hier het woord 'minimaal'?

(4p) Aan het einde van de horizontale baan werkt er geen aandrijvende kracht meer. Het (zwaartepunt van het) treintje gaat daarna 139 m omhoog. Natuurlijk moet de trein wel de top halen. Een bepaald percentage van de bewegingsenergie wordt tijdens de rit naar boven omgezet in warmte ten gevolge van de wrijving. Bereken hoe groot dit percentage maximaal mag zijn.

(bron: examen VWO 2010-1)

(VWO, 6p) Een wielrenner fietst op zijn hometrainer. Elke voet maakt een rotatie met een straal van 17,5 cm. Een meetsysteem meet de kracht van de voet op het pedaal. Deze kracht is als functie van de tijd hieronder weergegeven. De grafiek geldt voor één voet. Met zijn andere voet doet de wielrenner hetzelfde. Bepaal het vermogen dat de wielrenner levert.

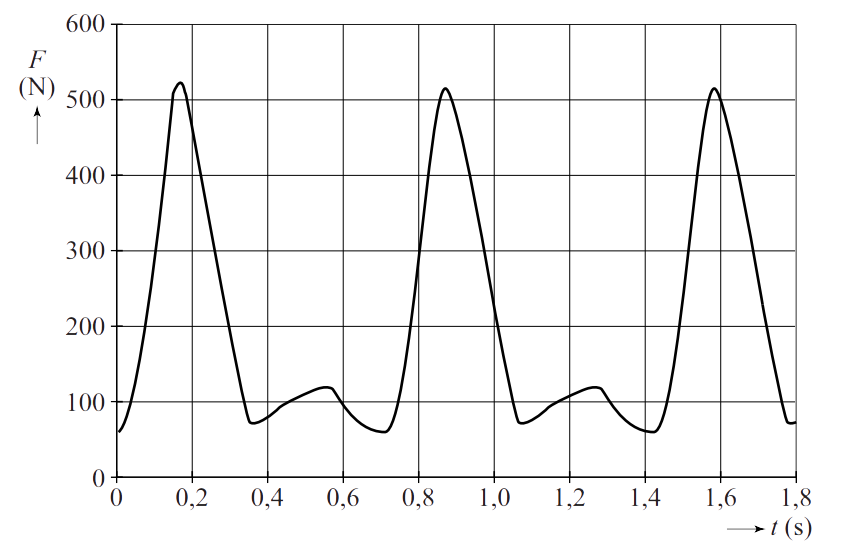
(bron: examen VWO 2014-1)

Een volleyballer maakt een verticale sprong. In het onderstaande diagram zien we het energieverbruik van de springer tijdens het afzetten.

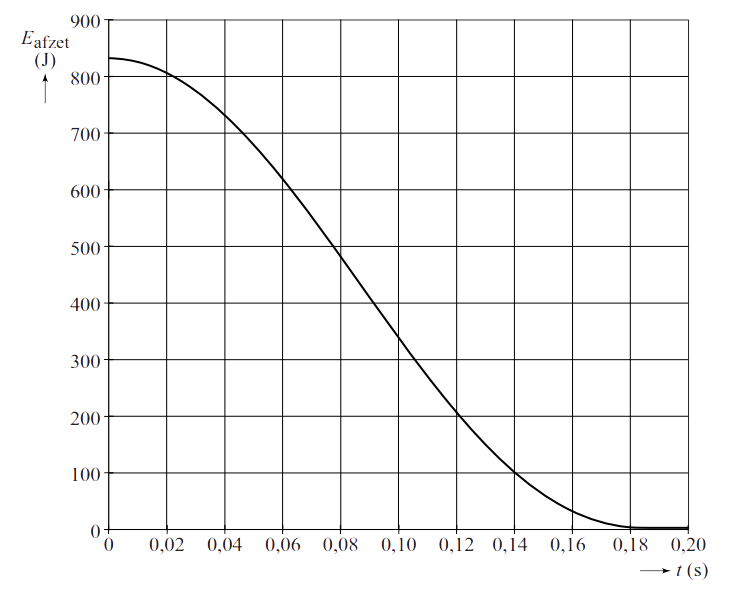
(2p) Bepaal met behulp van het figuur op welk tijdstip het vermogen van de springer maximaal is.

(2p) In het volgende figuur is de zwaarte-energie en de afzetenergie van de springer weergegeven. De kinetische energie is nog niet weergegeven.
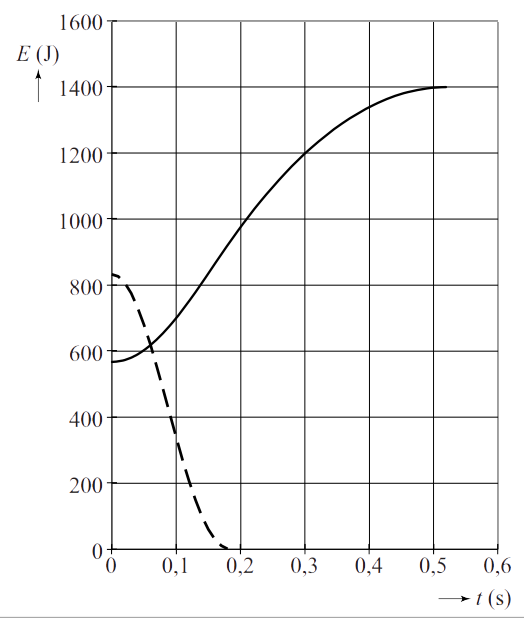
Leg uit dat de kinetische energie op t = 0 s en t = 0,5 s gelijk is aan nul.

(3p) Teken in het diagram de grafiek voor de kinetische energie. Je mag de warmte die ontstaat door de wrijvingskrachten verwaarlozen.

(bron: examen VWO 2015-1)

Bij een attractie in een pretpark kan men ondervinden hoe een 'vrije' val voelt. Een persoon wordt in een speciale cabine geplaatst die tot een bepaalde hoogte wordt opgetakeld (zie de onderstaande afbeelding). De cabine wordt in punt A losgelaten. Op het traject AB is de beweging op te vatten als een vrije val. Op traject BD is de baan cirkelvormig. Vanaf D is de baan horizontaal. Op het stuk DE komt de cabine tot stilstand. De snelheid van de cabine in punt B is 15,2 m/s.

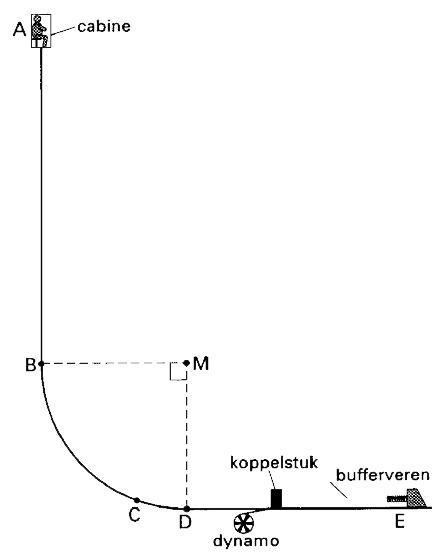
(3p) Bereken de afstand waarover de inzittende gewichtsloos valt.

(4p) Het zwaartepunt van de inzittende doorloopt op het traject BCD een kwart cirkel met een straal van 5,0 m. Op het stuk BCD is de wrijving niet te verwaarlozen. De massa van de cabine met inzittende is 250 kg. De gemiddelde wrijvingskracht is op dit traject 0,5 x 10³ N. Bereken de snelheid van de cabine op punt D.

(4p) Op het horizontale traject DE botst de cabine tegen een koppelstuk dat over de rail kan bewegen. Na de botsing blijft de cabine aan het koppelstuk vastzitten. Wrijving wordt op dit horizontale traject verwaarloosd. Aan het koppelstuk is een kabel bevestigd. De andere kant van de kabel is om de as van een dynamo gewikkeld. Zodra de kabel strak is getrokken, gaat de dynamo draaien. De opgewekte elektrische energie wordt in het pretpark gebruikt. Het koppelstuk heeft een massa van 30 kg. De snelheid van cabine en koppelstuk onmiddellijk na de botsing is 15 m/s. Het door de dynamo uitgeoefende remvermogen is dan 12 kW. Bereken de vertraging van de cabine met het koppelstuk op het eerste moment van het afremmen door de dynamo.

(3p) Indien deze manier van afremmen mislukt, zijn als beveiliging aan het einde van de baan twee bufferveren naast elkaar aangebracht. Neem aan dat het koppelstuk met cabine en inzittende dan met een snelheid van 15 m/s tegen deze veren botst. De veren worden dan 1,2 m ingedrukt. Bereken de veerconstante van één bufferveer.

(bron: examen VWO 1994-2)

§5 (F,s)-diagrammen (VWO)

In deze paragraaf gaan we de arbeid bepalen met (kracht,verplaatsing)-diagrammen.

We kunnen de geleverde arbeid ook uitrekenen met behulp van een (kracht,verplaatsing)-diagram. De oppervlakte onder deze grafiek is gelijk aan 'F×s' en dit is precies de geleverde arbeid.

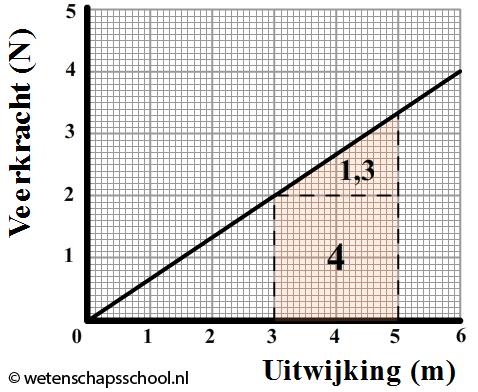
Hieronder zien we een (kracht,verplaatsing)-diagram van een veer. Stel we willen de energie bepalen die nodig is om een veer van u = 3,0 cm naar u = 5,0 cm te trekken. Het oppervlak onder de grafiek tussen deze twee uitwijkingen is gelijk aan 5,3 J. De veerenergie is dan dus met 5,3 J toegenomen.

Rekenen met de oppervlakte onder de (F,s)-diagram

Een persoon duwt een blok naar rechts over een wrijvingsloos oppervlak. Hieronder zien we het (F,s)-diagram van de beweging.

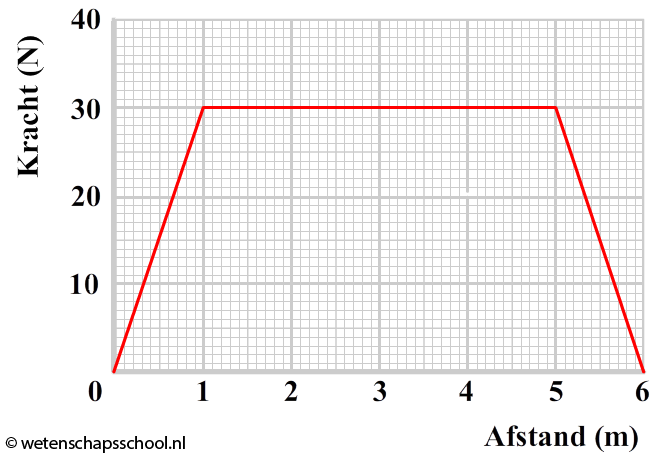
(2p) Leg voor elk deel van de grafiek uit of het blok versnelt, vertraagt of met een constante snelheid voortbeweegt.

(2p) Bereken de totale arbeid die verricht is bij het duwen van het blok.

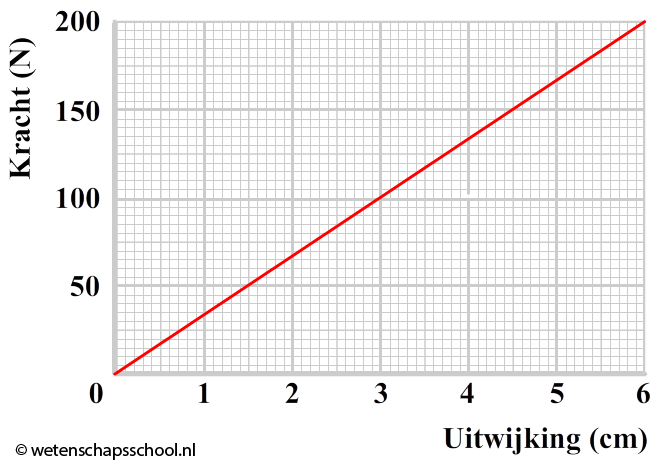
(2p) In de onderstaande afbeelding zien we een (F,u)-diagram van een veer. Bepaal met behulp van de grafiek de arbeid die de veer uitoefent als we de veer uitrekken van u = 1,0 cm naar u = 5,0 cm.

Vertical Shot is een nieuwe kermisattractie. Aan twee pilaren zijn elastieken vastgemaakt. Aan deze elastieken hangt een bol waarin twee personen plaatsnemen. De bol wordt met behulp van een elektromagneet op de grond gehouden, terwijl de elastieken aangespannen worden. Nadat de personen vastgegespt zijn, wordt de elektromagneet uitgezet en schiet de bol verticaal omhoog.
In de onderstaande grafiek is de kracht van beide elastieken uitgezet tegen de hoogte van de bol. Op een hoogte van 24 meter werken er geen krachten meer op de elastieken.
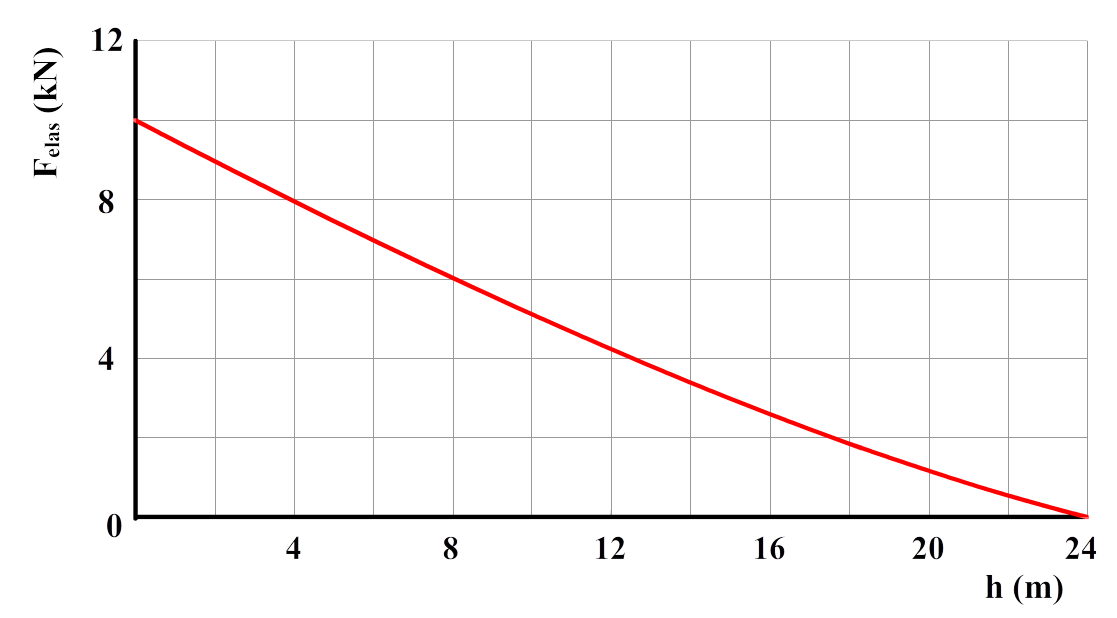
De bol met passagiers hebben samen een massa van 250 kg. We nemen in deze vraag aan dat de wrijvingskracht te verwaarlozen is.

(4p) De bol behaalt zijn maximale snelheid op een hoogte van 16 meter. Laat met behulp van de grafiek zien dat dit het geval is. (tip: bij een snelheidsmaximum is de snelheid even constant).

(4p) Bepaal de maximale hoogte die de bol bereikt.

(bron: examen VWO 2003-2)

Een polsstokhoogspringer van 80 kg maakt zich klaar voor een sprong met een stok van 6,0 m lang. Het zwaartepunt van de springer bevindt zich voor de sprong op een hoogte van 0,90 m en de stok met een massa van 3,0 kg bevindt zich in horizontale stand op dezelfde hoogte. De springer neemt een aanloop en vlak voor de afzet is de snelheid van de atleet met de polsstok 8,8 m/s. De springer plaatst zijn stok op de grond en met behulp van de veerkracht van de stok springt hij de lucht in. De atleet gaat dan met een te verwaarlozen horizontale snelheid gestrekt over de lat. Neem aan dat de polsstok wordt losgelaten als deze verticaal stilstaat op de grond.

(4p) Bereken de hoogte van het zwaartepunt van de springer op het moment dat hij over de lat gaat. De invloed van de luchtwrijving mag worden verwaarloosd.

(4p) Na het passeren van de lat komt de atleet neer op een dikke mat. De verplaatsing van het oppervlak van de mat door de vallende atleet wordt de uitwijking (u) genoemd. Ten gevolge van deze verplaatsing oefent de mat een veerkracht uit op de atleet. Hieronder is de veerkracht van de mat tijdens het neerkomen en terugveren van de atleet weergegeven. Vanaf het moment dat de atleet de mat treft, doorloopt hij de grafiek met de klok mee. Bij u = 45 cm komt de springer even tot stilstand en daarna veert de springer weer terug omhoog. Bepaal met behulp van het diagram met welke snelheid de atleet op de mat is geland.

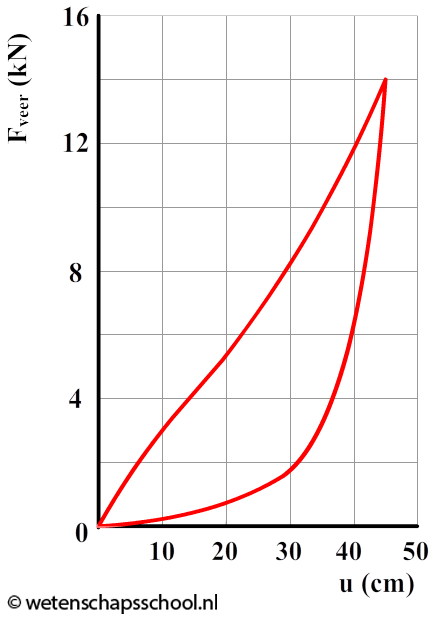
(3p) Na het terugveren blijkt dat een deel van de kinetische energie van de springer geabsorbeerd is door de mat. Laat met behulp van het bovenstaande diagram zien dat het hier gaat om 1,9 × 10³ J.

(bron: examen VWO 1985-2)

§6 Gravitatie-energie (VWO)

In deze paragraaf introduceren we de gravitatie-energie. We gaan deze energie o.a. gebruiken om uit te rekenen hoeveel energie nodig is om een voorwerp uit een gravitatieveld te laten ontsnappen.

Ook bij de gravitatiekracht hoort een energie. Deze wordt gegeven door:

$$E_g = -\frac{mMG}{r}$$

Gravitatie-energie (E_g)

joule (J)

Voorwerp met kleine massa (m)

massa (kg)

Voorwerp met grote massa (M)

massa (kg)

Gravitatieconstante (G)

6,67 x 10^-11 Nm²kg^-2

Baanstraal (r)

meter (m)

Aan deze formule kan je zien dat de gravitatie-energie altijd negatief is en dat de gravitatie-energie de nul joule nadert als de twee massa's erg ver van elkaar verwijderd zijn. Dit is ook te zien aan de onderstaande grafiek die hoort bij deze formule.

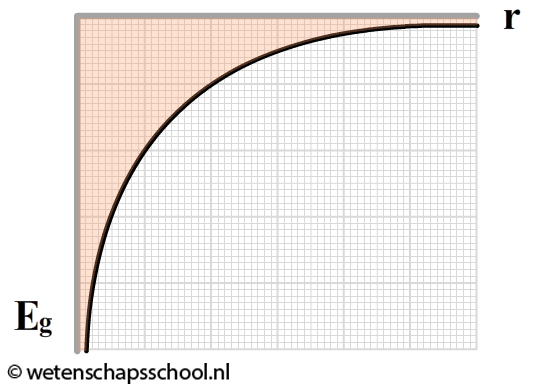
Met deze energie kunnen we o.a. de minimale snelheid uitrekenen die nodig is om een voorwerp te laten ontsnappen uit het gravitatieveld van bijvoorbeeld de aarde. We noemen deze minimale snelheid de ontsnappingssnelheid.

Stel we schieten een voorwerp weg van de aarde met net genoeg kinetische energie dat het kan ontsnappen. Op het moment waarop het voorwerp net is afgeschoten, heeft het voorwerp kinetische energie en gravitatie-energie. Op het moment dat het voorwerp ontsnapt is, is het voorwerp zijn kinetische energie verloren en is de gravitatie energie nul geworden. Er geldt dus:

$$E_{tot,b} = E_{tot,e}$$ $$E_{kin,b} + E_{g,b} = 0$$

Nu vullen we de formules in. Let op het minteken van de gravitatie-energie:

$$\frac{1}{2}mv_{b}^2 -\frac{mMG}{r_{b}} = 0$$ $$\frac{1}{2}mv_{b}^2 = \frac{mMG}{r_{b}}$$ $$v_{begin}^2 = \frac{2MG}{r_{b}}$$ $$v_{begin} = \sqrt{\frac{2MG}{r_b}}$$

De ontsnappingssnelheid is dus:

$$v_{ontsnapping} = \sqrt{\frac{2MG}{r_b}}$$

Ontsnappingssnelheid (v_ontsnapping)

meter per seconde (m/s)

Voorwerp met grote massa (M)

massa (kg)

Gravitatieconstante (G)

6,67 x 10^-11 Nm²kg^-2

Afstand tussen M en m bij afschieten (r_b)

meter (m)

Laten we de ontsnappingssnelheid van de aarde berekenen. Voor de straal r vullen we de straal van de aarde in. We vinden:

$$\sqrt{\frac{2 \times 5,9 \times 10^{24} \times 6,7 \times 10^{-11}}{6,4 \times 10^6}} = 11 \times 10^3 \text{ m/s}$$

De ontsnappingssnelheid van de aarde is dus 11 km/s.

Rekenen met de gravitatie-energie en de ontsnappingssnelheid

(4p) Een persoon wil berekenen hoe snel hij een kanonskogel omhoog zou moeten afschieten om deze te laten ontsnappen aan het gravitatieveld van de aarde. Bereken deze snelheid in km/s. Je mag de wrijvingskracht van de atmosfeer verwaarlozen.

(3p) Een planeet beweegt in een ellipsbaan om de zon. De totale energie van een planeet in een baan om de zon bestaat uit de som van zijn kinetische energie en zijn gravitatie-energie. Beredeneer hiermee dat een planeet dichter bij de zon een grotere snelheid heeft dan op grotere afstand van de zon.

(6p) Een terugkerende ruimtecapsule met een massa m = 5,8 × 10³ kg, bevindt zich op 500 km hoogte met baansnelheid van 7,5 × 10³ m/s. Om veilig te landen moet de capsule in de atmosfeer energie kwijtraken. Bereken de orde van grootte van dit energieverlies.

(6p) Een komeet met een massa van 12 × 10³ kg beweegt op een hoogte van 100 km boven het aardoppervlak met een snelheid van 50 km/s richting de aarde. Bij aankomst op de aarde is de massa van de komeet afgenomen tot 6,0 × 10³ kg. Het totaal van de kinetische energie en de gravitatie-energie is dan nog slechts 0,20% van de oorspronkelijke totale energie. Bereken met welke snelheid de komeet op de aarde aankomt.

Een ruimteschip gaat in een rechte baan van de aarde naar de maan.

(2p) Neemt de gravitatie-energie van het ruimteschip tijdens de lancering toe of af? Licht je antwoord toe.

(4p) Bij het opstijgen van het ruimteschip wordt gebruik gemaakt van een stuwraket. Nadat de stuwraket op een hoogte van 300 km boven het aardoppervlak wordt afgeworpen, moet het ruimteschip voldoende snelheid hebben om de maan te bereiken. De massa van het ruimteschip is 4,0 x 10³ kg. Bereken de orde van grootte van de minimale kinetische energie die het ruimteschip moet hebben op het moment van het afwerpen van de stuwraket om de maan te kunnen bereiken. De gravitatiekracht van de maan op de raket is te verwaarlozen.

Een communicatiesatelliet wordt met behulp van een raket in een geostationaire baan rond de aarde gebracht. Deze banen bevinden zich op een hoogte van 35,8 x 10³ km boven het aardoppervlak. De satelliet beweegt met een snelheid van 3,1 x 10³ m/s in zijn baan. De massa van de satelliet is 3,90 x 10³ kg.

(6p) Bereken de arbeid die de gravitatiekracht verricht als de satelliet vanaf de aarde naar zijn baan gebracht wordt.

(3p) Om het gemakkelijker te maken om deze arbeid te verrichten, wordt gebruik gemaakt van de draaiing van de aarde om zijn eigen as. Bereken de kinetische energie van de satelliet op de evenaar door de draaiing van de aarde.

(2p) Bereken hoeveel arbeid er dan nog minimaal door de motorkracht verricht moet worden om de satelliet in zijn baan te krijgen.

De verkenner Pioneer-10 werd gelanceerd in 1972 en was in 1983 het eerste ruimtevaartuig dat ons zonnestelsel verliet. In 1983 bewoog Pioneer-10 met een snelheid van ongeveer 2,6 AE per jaar in de richting van de rode ster Aldebaran.

(4p) Bereken hoeveel jaar Pioneer-10 over zijn reis naar Aldebaran zal doen als hij zijn hele reis met de gegeven snelheid beweegt.

(2p) In het begin van de reis wordt Pioneer-10 door de zon vertraagd. Aan het eind van zijn reis wordt Pioneer-10 door Aldebaran versneld. Tim en Maaike bespreken het effect hiervan op de gemiddelde snelheid van Pioneer-10. Tim denkt dat de gemiddelde snelheid minder dan 2,6 AE per jaar is door de invloed van de zon. Maaike meent dat de gemiddelde snelheid meer dan 2,6 AE per jaar is, omdat de massa van Aldebaran 25 keer zo groot is als de massa van de zon. Leg uit wie er gelijk heeft.

(6p) In 1983 bevond Pioneer-10 zich op een afstand r = 6,2 x 10¹² m van de zon. Toon aan dat zijn snelheid dan ruimschoots voldoende is om uit het zonnestelsel te ontsnappen.

(bron: examen VWO 2011-1)

§7 Modelleren met energie

In deze paragraaf gaan we een model maken met de begrippen energie en vermogen.

We kunnen ook modelleren met energie en vermogen. Hieronder zien we het model van een speelgoedautootje met een motor met een constant vermogen van 10 W. We verwaarlozen de rolwrijvingskracht, maar niet de luchtwrijvingskracht.

Laten we de modelregels stap voor stap bespreken. De tweede modelregel geeft een formule voor de luchtwrijvingskracht:

Fw = k*v^2

Met de wrijvingskracht kunnen we het vermogen van de wrijvingskracht berekenen met de formule P_w = F_wv. Het totale vermogen van de auto is gelijk aan het vermogen dat de motor levert (P_m) min het vermogen dat verloren gaat door de wrijvingskracht (P_w = F_wv). De modelregel wordt dus:

Ptot = Pm - Fw*v

Voor de volgende regel gebruiken we dat elk tijdstapje de toename van de energie (ΔE) wordt toegevoegd aan de kinetische energie:

Ek = Ek + dE

Voor dE gebruiken we dan de formule ΔE = PΔt. We vinden hiermee:

Ek = Ek + P*dt

Als we de formule voor de kinetische energie omschrijven, dan kunnen we hiermee de snelheid uitrekenen. De volgende modelregel wordt daarom:

v = sqrt(2*Ek/m)

Met de snelheid kunnen we de dan zoals gebruikelijk de nieuwe positie berekenen:

x = x + v*dt

Laten we nog een laatste voorbeeld bespreken. Hieronder zien we het model van een kleine raket. De raket zelf heeft een massa van 100 kg en bevat 1000 kg brandstof. De stookwaarde van deze brandstof is 10000 J/kg. Zolang de raket brandstof heeft levert het een kracht van 50000 N.

In de tweede regel (mtot = mr + mb) wordt de totale massa van de raket berekend en met de derde regel (Fz = mtot*g) wordt hiermee de zwaartekracht werkende op de raket uitgerekend. De twee regels die hierop volgen (als(mb<0) dan{Fm=0}) zorgen ervoor dat de motorkracht op nul komt te staan als de brandstof op is.

In de één-na-laatste regel (W = Fm*dx) wordt de arbeid uitgerekend die de motor in het tijdstapje verricht heeft. Deze arbeid is gelijk aan de motorenergie die in dit tijdstapje gebruikt is (W_m = E_m).

In de laatste zin (mb = mb - W/stook) hebben we gebruik gemaakt van de formule E_ch = r_mΔm, waarbij Δm de massa is van de brandstof die tijdens het tijdstapje verbrand is. Als we deze formule omschrijven, dan vinden we:

$$\Delta m = \frac{E_{ch}}{r_m}$$

Omdat we kunnen aannemen dat de motor geen energie verliest, kunnen we dit herschrijven tot:

$$\Delta m = \frac{E_m}{r_m}= \frac{W_m}{r_m}$$

In de laatste modelregel wordt deze massa van de totale brandstof afgehaald.

Modelleren met energie en vermogen

In de volgende afbeelding is een model gemaakt van een voertuig dat vanuit stilstand met een constant motorvermogen vooruit beweegt. In het linker model zijn de wrijvingskrachten verwaarloosd.

(3p) Vul de ontbrekende modelregels aan in het linker model. Leg uit hoe je op dit antwoord gekomen bent.

(5p) In het rechter diagram is ook een luchtwrijvingskracht toegevoegd. Vul de ontbrekende modelregels aan.

In het volgende model wordt het bewegen van een klein vliegtuig op een landingsbaan beschreven tot het moment dat het vliegtuig van de grond komt.

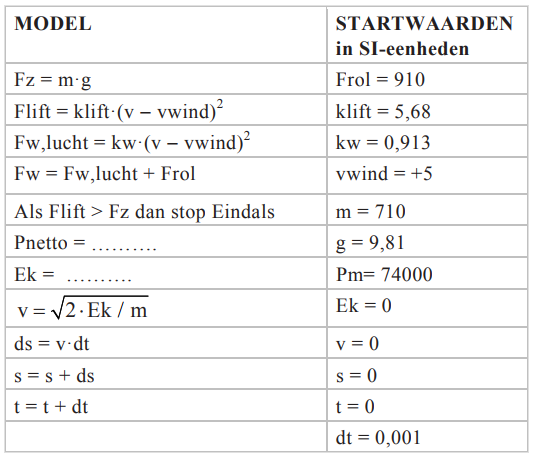
(4p) Vul de modelregels aan.

(2p) In het model wordt ook rekening gehouden met wind. Leg uit of in het model sprake is van tegenwind of van meewind.

(bron: examen VWO 2017-1)

(2p) Een verstrooide wetenschapper fantaseert over het bouwen van een lift die helemaal de ruimte in gaat. Hij maakt een model van de beweging van de lift. In zijn model is de lift voorzien van een brandstofmotor. Voor het gemak neemt de wetenschapper aan dat deze motor een rendement heeft van 100%. Hieronder staat het model beschreven:
Vul modelregel 9 aan.
(bron: examen VWO 2016-1)

BINAS:
28B	Stookwaarden
7	Gravitatieconstante

Hoofdstuk 1 Energie