Hoofdstuk 5
Elektriciteit II
§1 Elektriciteit in huis
§2 Capaciteit
§3 De transistor, de NTC, de LDR en de condensator
§4 De spoel
§5 De transformator
§1 Elektriciteit in huis
In dit hoofdstuk gaan we verder met het bestuderen van elektrische schakelingen. We gaan hier met name kijken naar toepassingen. Het is handig hoofdstuk "Elektriciteit I" nog even door te nemen voordat je aan dit hoofdstuk begint. In deze eerste paragraaf gaan we het hebben over het elektriciteitsnetwerk in huis.
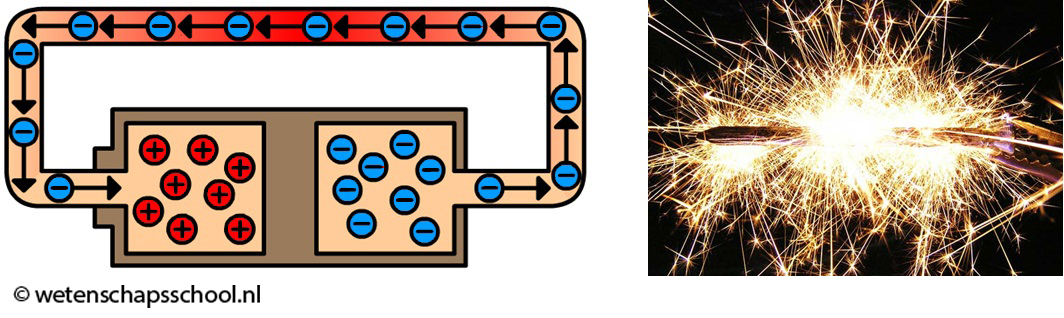
Als we de pluspool en de minpool van een spanningsbron direct verbinden met een materiaal met een erg kleine weerstand, dan ontstaat er kortsluiting. Door de kleine weerstand gaat er dan een grote stroom door het materiaal lopen (zie de linker onderstaande afbeelding). Deze grote hoeveelheid stroom kan gevaarlijk zijn voor de mens en kan ook gemakkelijk brand veroorzaken doordat er warmte en vonken vrijkomen (zie de rechter afbeelding).
 (Afbeelding: ... / MdE; CC BY-SA 3.0)
(Afbeelding: ... / MdE; CC BY-SA 3.0)
 Demonstratievideo
Demonstratievideo
|
|
In het rechter filmpje zien we hoeveel warmte er kan ontstaan bij kortsluiting:
|
 DEMO-VIDEO:
Kortsluiting
DEMO-VIDEO:
Kortsluiting
|
|
 Demonstratievideo
Demonstratievideo
|
|
Hiernaast zien we hetzelfde effect, maar dan bij hoogspanningskabels. Misschien heb je wel eens een vogel op een hoogspanningskabel zien zitten (zie de afbeelding onder het filmpje). Een vogel lijkt zich hier niet aan te storen. Dit komt omdat de vogel slechts één draad raakt en daarom geen onderdeel van een gesloten stroomkring vormt. In het onderstaande filmpje is een tak op hoogspanningskabels gevallen die twee kabels met elkaar verbindt. Nu is er wel een gesloten stroomkring! Hetzelfde gebeurt als er een verbinding is tussen een kabel en de grond (ook de grond kan vaak stroom geleiden).
|
 DEMO-VIDEO:
Kortsluiting II
DEMO-VIDEO:
Kortsluiting II
|
|

In het elektriciteitsnetwerk in huis kan als volgt kortsluiting ontstaan. Als je een stopcontact van de muur schroeft (doe dit niet zonder begeleiding en zet eerst de groep uit waartoe het stopcontact behoort!), dan zijn drie draden zichtbaar (zie de onderstaande foto). De bruine draad is de zogenaamde fasedraad. Hierover staat een spanning. De blauwe draad is de nuldraad. Hierover staat geen spanning. Als deze twee draden verbonden worden, dan ontstaat kortsluiting. Als deze draden worden aangesloten op een elektrisch apparaat met een redelijke weerstand, dan hebben we een functionele gesloten stroomkring en gaat het apparaat werken. De geel-groene draad in de afbeelding bespreken we later in de paragraaf.

Om ons tegen kortsluiting te beschermen bevat de meterkast in huis een aantal zekeringen. Een ouderwetse zekering bestaat uit een draadje dat doorbrandt als de stroomsterkte boven een bepaalde waarde uitkomt. In de onderstaande afbeelding zien we bijvoorbeeld een zekering die bij 20 A doorbrandt.

In de onderstaande afbeelding zien we een voorbeeld van een meterkast. Onder in deze kast zie je de voedingskabel waardoor elektriciteit het huis binnenkomt. Daarboven zien we een grote hoofdschakelaar. Hiermee kan de spanning in het hele huis uit- en aangezet worden.
Daarnaast vinden we één of twee aardlekschakelaren. Een aardlekschakelaar vergelijkt de stroom die het huis ingaat met de stroom die het huis uitgaat. Als het goed is moeten beide stromen gelijk zijn. Als dit niet zo is, dan moet er ergens in huis stroom zijn weggelekt (bijvoorbeeld via iemands lichaam naar de grond). Dit is gevaarlijk en als voorzorgsmaatregel wordt de stroom dan direct uitgezet.
Boven de aardlekschakelaren zien we de groepenkast met daarin een hele rij zekeringen. In dit geval zien we moderne zekeringen die niet meer werken met het doorbranden van een draadje, maar met een schakelaar. Het voordeel hiervan is dat deze zekeringen niet elke keer vervangen hoeven te worden nadat ze doorbranden.
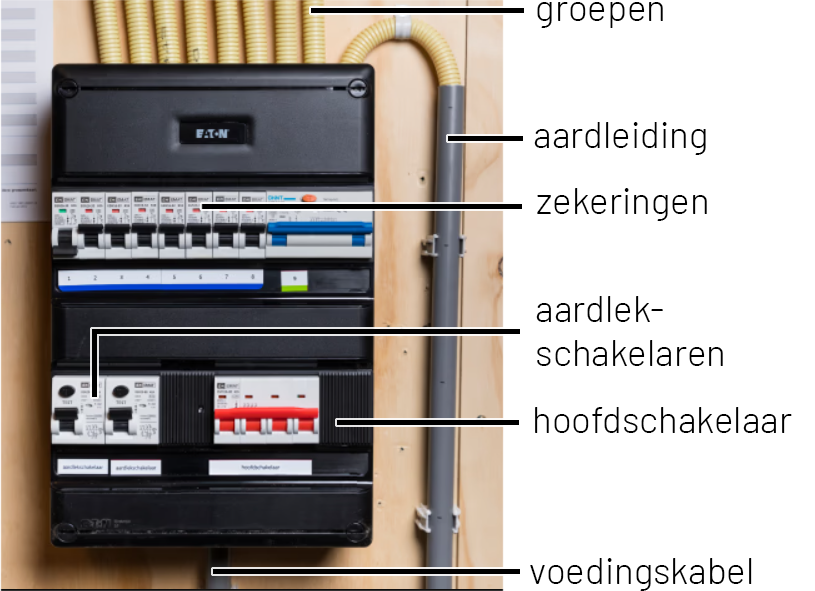
Aan de rechterkant van de meterkast zien we de aardleiding. Dit is een draad die letterlijk de aarde in loopt. Deze draad is in huis verbonden met metalen onderdelen van apparaten waarvan het gevaarlijk zou zijn als ze onder spanning staan. Denk bijvoorbeeld aan de buitenzijde van een wasmachine of een waterkoker. Als deze onderdelen onder spanning komen te staan, dan gaat er een stroom lopen via de aardedraad naar de grond. De aardlekschakelaar zal de stroom dan uitschakelen. Als gevolg voorkom je dat er een stroom door je lichaam loopt als je deze onderdelen aanraakt.
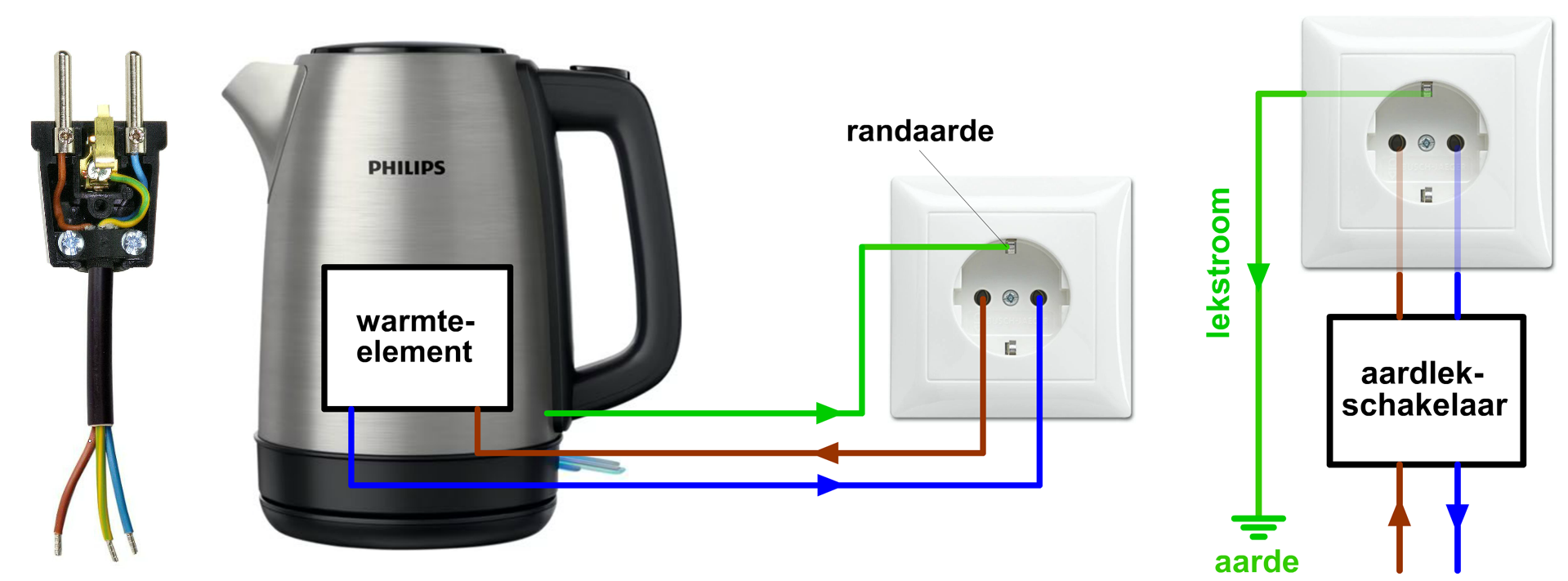
In de onderstaande afbeelding is dit schematisch afgebeeld. Links is de draad van een waterkoker opgesneden. Je ziet hierin o.a. de blauwe fasedraad en de bruine nuldraad. Deze draden worden gebruikt om een gesloten stroomkring te maken, waardoor het warmte-element in de waterkoker warm wordt. De geel-groene draad is de aardedraad. Deze draad is verbonden met de buitenzijde van de waterkoker en staat in contact met de twee metalen pinnen boven en onder het stopcontact. We noemen dit de zogenaamde randaarde (zie de middelste afbeelding). Deze pinnen zijn weer verbonden via de aardleiding met de aarde onder het huis (zie de rechter afbeelding).
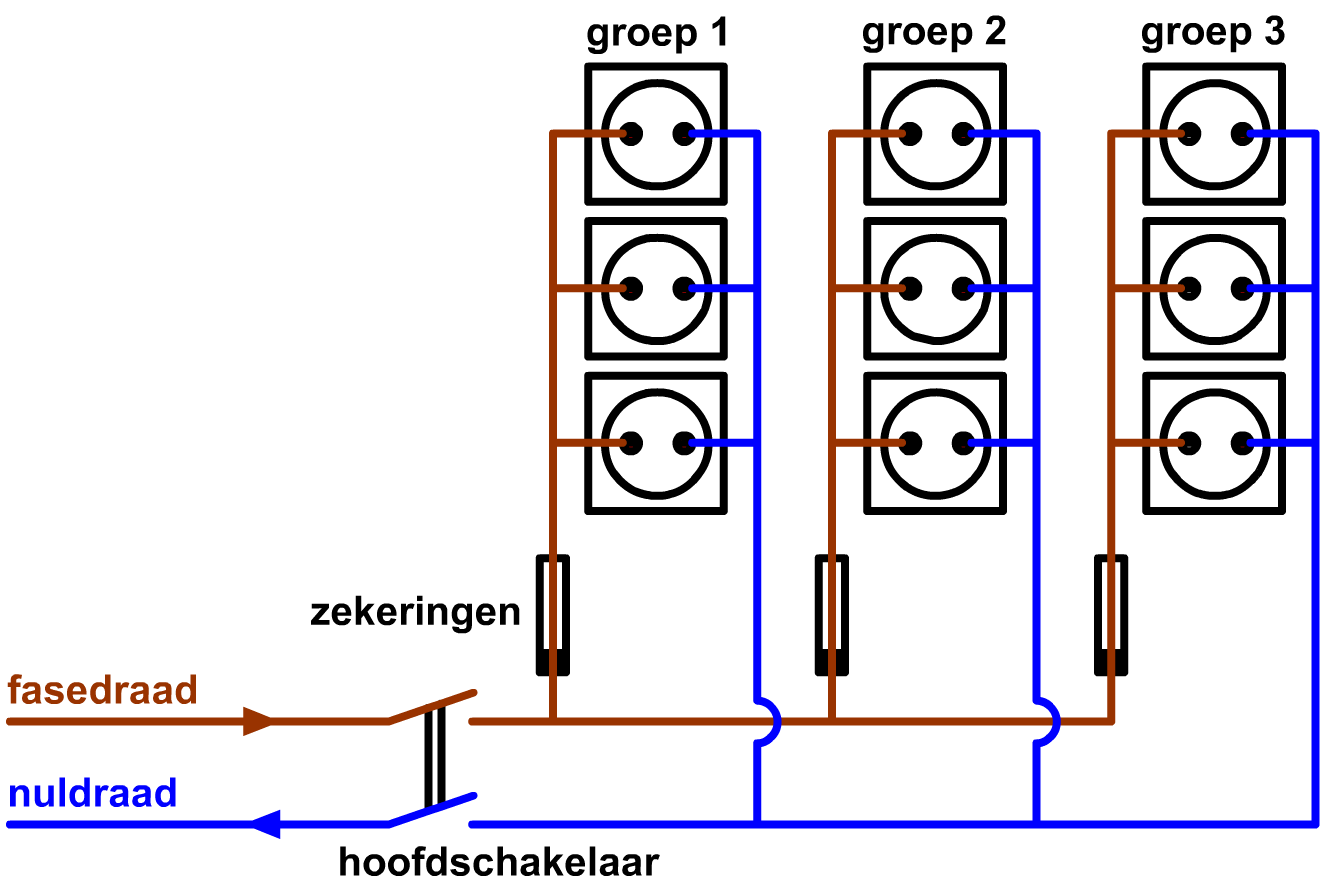
Vanaf elke zekering in de meterkast loopt een draad naar boven. Deze draden splitsen op en zijn verbonden met de vele stopcontacten in huis. Voor de veiligheid zijn de stopcontacten in huis opgedeeld in een aantal groepen, elk met een eigen zekering (zie de onderstaande afbeelding).
Apparaten die een grote stroom vragen, zoals de wasmachine of een elektrische kookplaat wil je niet allemaal op dezelfde groep zetten, want dan kunnen de draden te warm worden en kan brand ontstaan. In dat geval spreken we van overbelasting. De zekeringen zorgen ervoor dat de stroom dan wordt uitgeschakeld.
 Leerdoelen:
Leerdoelen:
|
- Zorg dat je weet dat kortsluiting ontstaat als we de plus- en de minpool van een spanningsbron verbinden met een draad met een kleine weerstand. Er gaat hierdoor een grote stroom lopen. In huis ontstaat kortsluiting als de fasedraad (bruine draad) en de nuldraad (blauwe draad) direct met elkaar verbonden worden.
- Zorg dat je weet dat overbelasting ontstaat wanneer te veel onderdelen die een grote stroom vragen op dezelfde groep worden aangesloten. De draden worden hierdoor gevaarlijk warm.
- Zorg dat je weet dat een zekering de stroom verbreekt als de stroomsterkte door de zekering boven een bepaalde waarde uitkomt. Dit gebeurt bij kortsluiting, maar ook bij overbelasting. En zorg dat je weet dat elke groep in huis zijn eigen zekering heeft.
- Zorg dat je weet dat een aardlekschakelaar de stroom die het huis in gaat vergelijkt met de stroom die het huis uitstroomt. De stroom wordt uitgeschakeld als er stroom is weggelekt.
- Zorg dat je weet dat metalen onderdelen van apparaten soms verbonden zijn met een geel-groene aardedraad die via de randaarde van het stopcontact naar de aarde loopt. Als deze metalen onderdelen onder spanning staan, dan loopt de stroom via de aardedraad naar de grond.
|
 Opdrachten
Opdrachten
|
- (1p) Kortsluiting treedt op als de plus en de min van een spanningsbron worden verbonden met een materiaal met een erg lage / erg hoge weerstand. Hierdoor gaat een kleine / grote stroom door de draad lopen.
- (1p) Leg uit waarom een zekering belangrijk is bij kortsluiting.
-
Apparaten die een grote stroom vragen, zoals de wasmachine of een elektrische kookplaat, mogen niet op dezelfde groep aangesloten worden.
- (1p) Leg uit waarom dit niet mag.
- (1p) Hoe noemen we dit?
- (1p) Schakelt ook hier een zekering de stroom uit?
- (2p) De twee gaten van het stopcontact zijn verbonden met een bruine en een blauwe draad. Hoe heten deze draden en wat gebeurt er als deze draden elkaar raken?
- In een draad van een lamp zitten minimaal twee draden (zie de onderstaande afbeelding). Waarom zijn er minimaal twee draden nodig?

-
Een leerling knipt per ongeluk een draad van een lamp door die is aangesloten op het stopcontact. Hierdoor is een vonk zichtbaar, er ontstaat een gat in het metaal van de schaar en daarna wordt de stroom uitgeschakeld.
- (1p) Hoe heet dit fenomeen?
-
(1p) Wanneer treedt dit fenomeen op. Kies uit:
- als de fasedraad de aardedraad raakt
- als de nuldraad de aardedraad raakt
- als de fasedraad de nuldraad raakt
- als de stroomsterkte door de lamp te groot is
-
(1p) Leg uit waarvoor de randaarde dient bij stopcontacten.
-
(1p) Waarom zijn in badkamers stopcontacten altijd geaard?
-
(1p) Als het koud is kun je een elektrische kachel op netspanning als bijverwarming gebruiken. De buitenkant van de kachel is van staal gemaakt en dit staal is geverfd om het tegen corrosie te beschermen. Leg uit of het aansluitsnoer een stekker met randaarde moet hebben.
(Bron: Examen VMBO-T, 2022-1)
-
Een elektrische kachel in een huis is voorzien van een stekker met randaarde. Elke groep in het huis heeft een zekering van 16 A. In de onderstaande afbeelding zijn drie gevaarlijke situaties weergegeven.
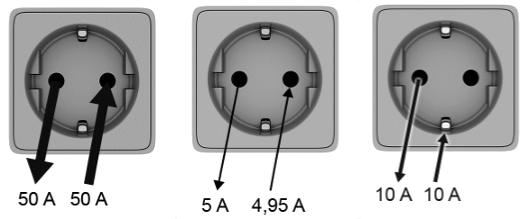
- (1p) Leg uit in welke situatie of situaties er stroom door de randaarde loopt.
- (2p) Leg uit in welk geval of in welke gevallen de aardlekschakelaar de stroom zal uitzetten.
- (1p) Leg uit in welk geval of gevallen de zekering zal doorbranden.
(Bron: Examen VMBO-T, 2021-1)
-
Een leerling hangt een dompelaar (een verwarmingselementje) in een theeglas met water. Aan het snoer van de dompelaar zit een stekker met randaarde.
- (1p) Leg uit dat het metaal aan de buitenzijde van de dompelaar niet verbonden mag zijn met de nuldraad, de fasedraad en het verwarmingselement in de dompelaar.
- (1p) Wanneer schakelt de aardlekschakelaar de spanning over de dompelaar uit? Kies uit:
- als de fasedraad de nuldraad raakt
- als de fasedraad het metaal aan de buitenzijde van de dompelaar raakt
- als de stroomsterkte door de dompelaar te groot is
- als de weerstand van de dompelaar te groot is
(Bron: Examen VMBO-T, 2019-1)
-
Het elektriciteitsnetwerk in huis bestaat uit een aantal groepen die elk zijn beveiligd met een zekering van 20 A. De volgende apparaten worden op één groep aangesloten:
- Een koelkast (200 W)
- Een magnetron (1500 W)
- Een wasmachine (4000 W)
- (1p) Leg zonder berekening uit of deze installatie een verstandig plan is.
- (5p) Laat met een berekening zien of er sprake is van overbelasting of niet. Gebruik hiervoor de formule "P = UI".
|
§2 Capaciteit
In deze paragraaf gaan we rekenen aan hoe lang een batterij of accu stroom kan leveren. We gebruiken daarvoor het begrip capaciteit.
De totale lading die in een batterij of accu opgeslagen zit noemen we de capaciteit (C). Hoe snel de batterij leegloopt hangt af van deze capaciteit en ook van hoeveel lading er per seconde wegstroomt uit de spanningsbron—oftewel, van de stroomsterkte. In formuletaal ziet dit er als volgt uit:
$$ t = \frac{C}{I} $$
|
Tijdsduur dat de batterij mee gaat (t)
|
uur (h)
|
|
Capaciteit (C)
|
milliampère-uur (mAh)
|
|
Stroomsterkte (I)
|
milliampère (mA)
|
|
Een veelgebruikte eenheid van de capaciteit is mAh, oftewel milliampère-uur. Als je deze eenheid gebruikt, dan moet je de stroomsterkte in de formule invullen in milliampère (mA) en de tijd in uren (h). Soms wordt ook Ah gebruikt. In dat geval moet de stroomsterkte worden gegeven in A en de tijd in h.
 Voorbeeld
Voorbeeld
|
|
Vraag:
Een accu in een telefoon heeft een capaciteit van 2600 mAh. De gemiddelde stroom die een telefoon gebruikt bij normaal gebruik is 0,7 A. Bereken hoe lang de telefoon te gebruiken is voordat de accu helemaal leeg is.
Antwoord:
De capaciteit is gelijk aan:
C = 2600 mAh
Omdat de capaciteit gegeven is in mAh, moeten we de stroomsterkte omrekenen naar mA. Er geldt:
I = 0,7 × 1000 = 700 mA
Nu kunnen we de tijdsduur uitrekenen tot de telefoon leeg is:
$$ t = \frac{C}{I} $$
$$ t = \frac{2600}{700} = 3,7 \text{ h} $$
Deze accu is dus 3,7 uur te gebruiken.
|
 Leerdoelen:
Leerdoelen:
|
- Zorg dat je kan rekenen met de formule "t = C/I". De capaciteit geeft aan hoeveel lading is opgeslagen in bijvoorbeeld een batterij of accu en wordt gemeten in bijvoorbeeld mAh of Ah.
|
 Opdrachten
Opdrachten
|
-
(2p) De capaciteit van de volledig opgeladen accu is 720 mAh. Er wordt een led op de accu aangesloten waaraan de accu een stroomsterkte van 200 mA levert. Bereken hoelang de lamp met een volledig opgeladen accu kan blijven branden.
-
(2p) De totale stroomsterkte door een led is 80 mA. Twee opgeladen batterijen hebben samen een capaciteit van 1800 mAh. Bereken hoelang de lamp kan branden op volledig opgeladen batterijen.
(Bron: Examen VMBO-T, 2023-2)
-
(2p) Een heftruck heeft een elektromotor om zware pakketten op te tillen. Tijdens het optillen van een pakket is de stroomsterkte door de elektromotor 135 A. De capaciteit van de opgeladen accu is 360 Ah. Bereken de maximale tijd dat de accu deze stroom kan leveren.
(Bron: Examen VMBO-T, 2022-2)
-
(2p) Een paar leds zijn aangesloten op een batterij. De batterij levert 410 mA en de capaciteit van de batterij is 1200 mAh. Bereken hoelang deze batterij maximaal energie kan leveren.
-
Het opladen van een bepaalde mobiele telefoon via een adapter duurt 90 minuten. Op de adapter lezen we: "230 V; 0,15 A".
- (4p) Bereken de capaciteit van de accu van de telefoon in mAh.
- (3p) Bereken hoe lang de accu meegaat als de accu gemiddeld een stroomsterkte van 0,090 A levert tijdens gebruik.
-
Een adapter levert bij het opladen van een accu (5,0 V) een stroomsterkte van 0,12 A. Het opgenomen vermogen van de adapter tijdens het opladen is 2,0 W.
- (3p) Bereken het rendement van de adapter (tip: gebruik "P = UI").
- (2p) Het volledig opladen van een lege accu duurt 2,8 h. Bereken de capaciteit van deze accu.
(Bron: Examen VMBO-T, 2019-2)
-
(4p) Bij een blikseminslag loopt in 8 milliseconden een stroomsterkte van 937 A van een wolk naar de aarde. Bereken de capaciteit van de bliksemschicht in mAh.
|
§3 De transistor, de NTC, de LDR en de condensator
In de rest van dit hoofdstuk gaan we een aantal geavanceerde elektrische componenten bestuderen. In deze paragraaf bespreken we de transformator, de NTC, de LDR en de condensator. Ook bespreken we hoe deze onderdelen toegepast worden in ons dagelijks leven.
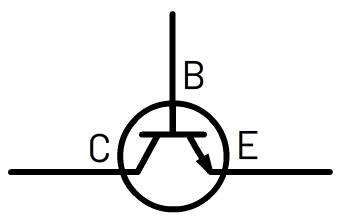
Een transistor is een elektrische schakelaar (zie de linker onderstaande afbeelding). Dit onderdeel werkt als volgt. Zoals je kunt zien heeft een transistor drie aansluitingen. We noemen deze aansluitingen de collector (C), de basis (B) en de emitter (E) (zie de rechter afbeelding). Als er een klein stroompje loopt door de basis ingang (B), dan gaat de schakelaar open en kan er een stroom lopen van de collector (C) naar de emitter (E). Het is belangrijk te weten dat de basis van de transistor een relatief grote weerstand heeft.

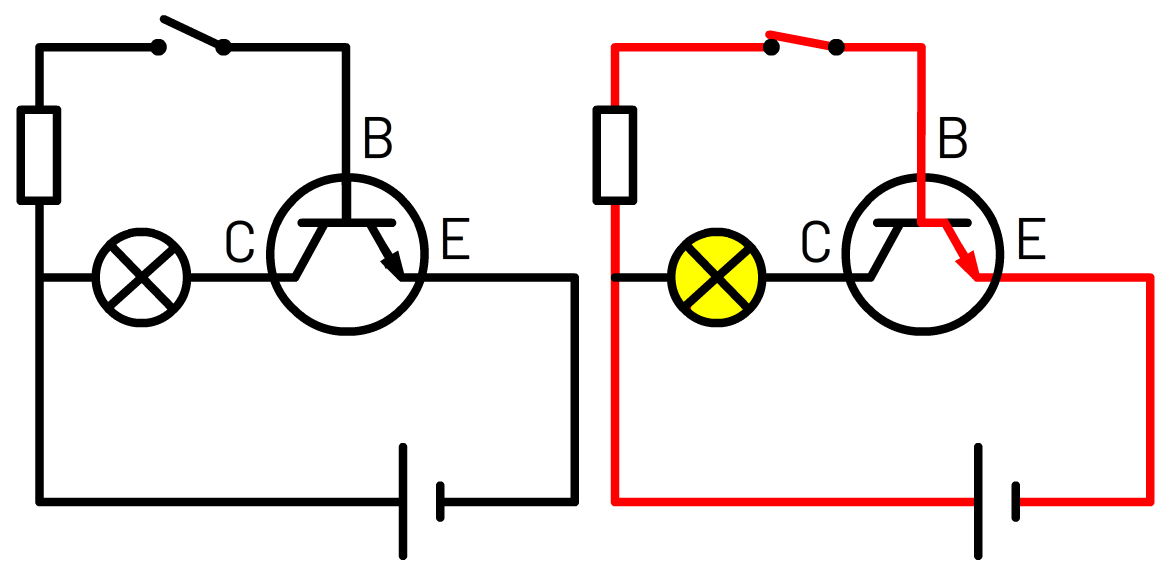
Laten we beginnen met een simpel voorbeeld om te begrijpen hoe de transistor werkt. Boven in de onderstaande schakeling zien we een handmatige schakelaar. Als deze open staat (zoals in de linker schakeling), dan komt er geen stroom bij de basis (B) binnen en als gevolg laat de transformator geen stroom door van de collector (C) naar de emitter (E). Als gevolg blijft de lamp uit. Als we de handmatige schakelaar indrukken (zoals rechts te zien is), dan komt er wel stroom binnen bij B en als gevolg laat de transistor wel stroom door van C naar E en gaat de lamp aan.
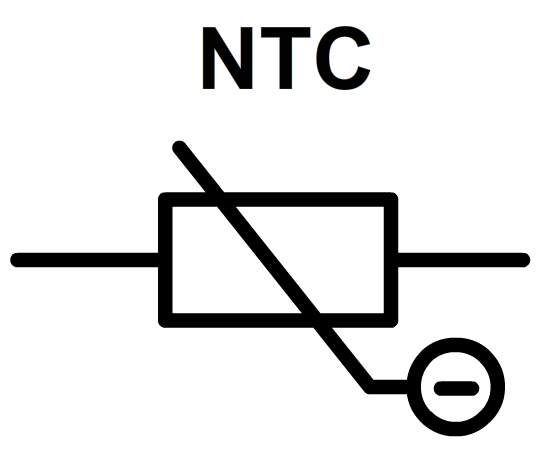
Nu gaan we een aantal onderdelen bespreken die samen met een transistor handige schakelingen opleveren. Een van deze onderdelen is de NTC. De NTC is een weerstand waarvan de waarde afhangt van de temperatuur. Hoe hoger de temperatuur, hoe lager de weerstand. Een gerelateerd onderdeel is de PTC. Hier geldt: hoe hoger de temperatuur, hoe hoger de weerstand. Deze componenten worden gebruikt als temperatuursensoren, waarmee de temperatuur gemeten kan worden. We gebruiken dit bijvoorbeeld in een thermostaat waarmee je de temperatuur in huis kan instellen.

 Demonstratievideo
Demonstratievideo
|
|
In het rechter filmpje is de werking van een NTC en een PTC gedemonsteerd. Beide onderdelen worden verwarmd met een föhn en op het scherm kan je zien wat dit doet met de weerstand. Ter vergelijking wordt daarna ook een normale vaste weerstand verwarmd. Deze waarde blijft constant.
|
 DEMO:
De NTC
DEMO:
De NTC
|
|
 Demonstratievideo
Demonstratievideo
|
|
In het rechter filmpje zien we een praktische toepassing van een NTC. Met een NTC kunnen we bijvoorbeeld een schakeling maken waarbij een ventilator automatisch aan gaat als de temperatuur hoog is en uit gaat als de temperatuur laag is:
|
 DEMO:
De NTC II
DEMO:
De NTC II
|
|
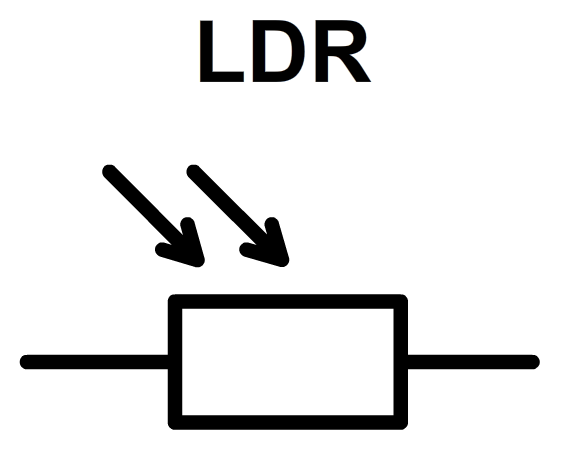
Een ander onderdeel is de LDR. Dit is een weerstand waarvan de waarde afhangt van de lichtintensiteit die erop valt. Er geldt dat hoe meer licht er op de LDR valt, hoe lager de weerstand van de LDR is. Deze component kan bijvoorbeeld gebruikt worden als lichtsensor. Misschien heb je wel eens gemerkt dat je telefoonscherm automatisch helderder wordt als je je telefoon in de felle zon houdt (of minder helder in het donker). Dit wordt bijvoorbeeld gedaan met een LDR.

 Demonstratievideo
Demonstratievideo
|
|
Hiernaast is een grappig experimentje te zien met een LDR. De LDR is aangesloten op een zogenaamde oscilloscoop. Hoe hoger de spanning over de oscilloscoop, hoe hoger een lichtpuntje op de oscilloscoop zichtbaar wordt. Als het lichtpuntje dicht bij de LDR komt, dan gaat door dit licht de weerstand van de LDR omlaag, waardoor de spanning over de oscilloscoop omhoog gaat en het lichtpunt over de LDR heen springt.
|
 DEMO:
De LDR
DEMO:
De LDR
|
|
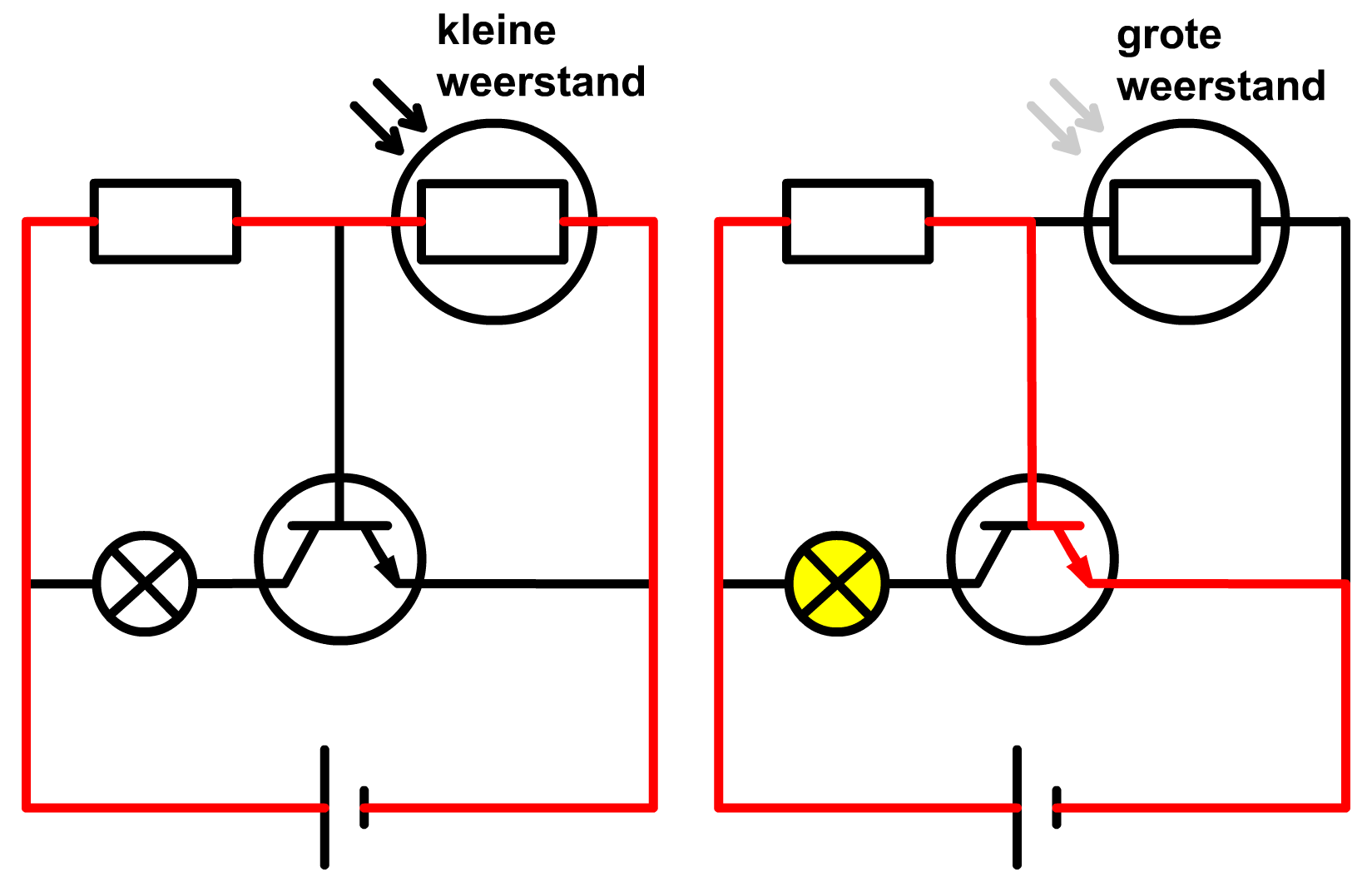
In de onderstaande schakelaar combineren we de LDR met de transistor. Deze schakeling zorgt ervoor dat een lamp automatisch aangaat als het donker wordt. De linker schakeling geeft de situatie overdag weer. In dat geval valt er zonlicht op de LDR. Als gevolg is de weerstand van de LDR laag en hierdoor loopt de meeste stroom door de LDR en dus niet door de B-ingang van de transistor (die een grote weerstand heeft). Als gevolg gaat het licht niet aan. In de nacht (zie de rechter schakeling) schijnt er geen licht op de LDR. In dat geval is de weerstand van de LDR hoog en als gevolg loopt de meeste stroom nu wel door de B-ingang van de transistor en gaat de lamp automatisch aan.
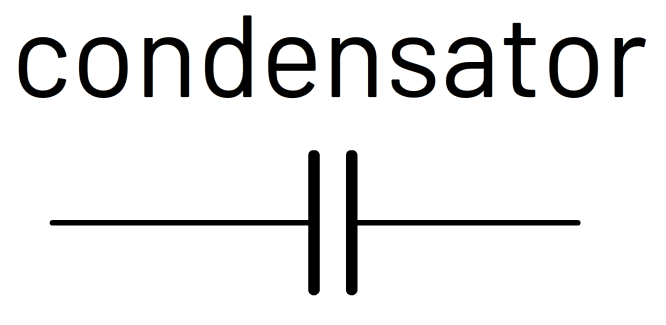
Een condensator is een onderdeel dat we kunnen opladen en ontladen. Een condensator bestaat uit twee metalen plaatjes die zich dicht naast elkaar bevinden. Het symbool ervoor zijn twee lange strepen (zie de onderstaande afbeelding).

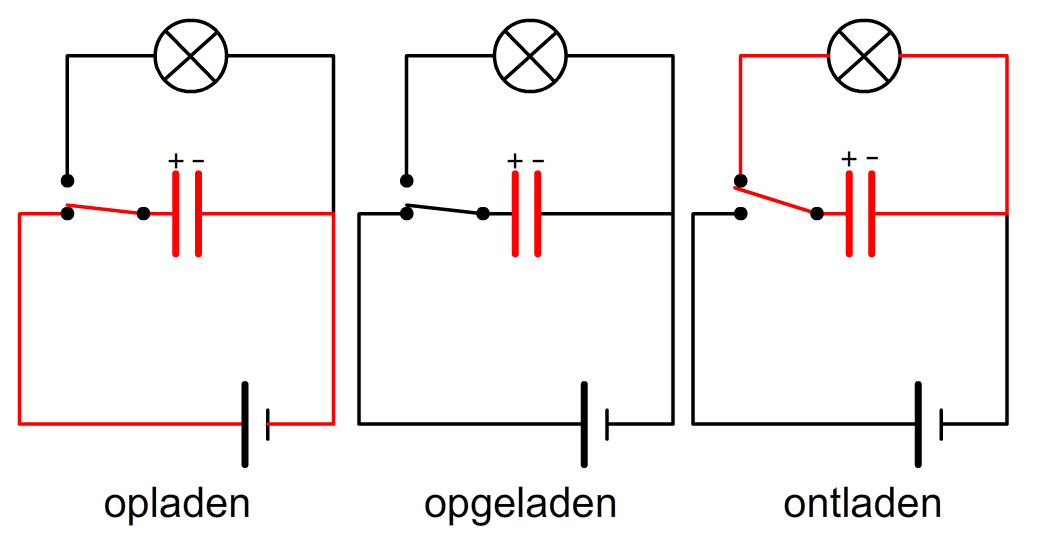
In de onderstaande linker schakeling wordt een condensator opgeladen met behulp van een spanningsbron. De linker plaat van de condensator is verbonden met de positieve pool van de spanningsbron en wordt daarom positief geladen. De rechter plaat is verbonden met de negatieve pool en wordt dus negatief geladen. Elke condensator heeft een maximale hoeveelheid lading dat het kan vasthouden. Als deze hoeveelheid bereikt is, dan is de condensator maximaal opgeladen en gaat er geen stroom meer naartoe (zie de middelste afbeelding). In de rechter afbeelding wordt een schakeling overgehaald, waardoor de condensator plots onderdeel wordt van een stroomkring met een lamp. De condensator zal nu ontladen, waardoor de lamp aan gaat. Hoe lang de condensator blijft branden hangt af van de weerstand van de lamp. Hoe hoger de weerstand, hoe langer de lamp blijft branden.
Condensatoren hebben veel toepassingen. Ze worden bijvoorbeeld gebruikt bij de flits van een camera. Voor deze flits is meer energie nodig dan de accu van een camera direct kan leveren. Daarom wordt eerst lading verzameld op de condensator en dit wordt dan in één keer ontladen om de flits te produceren.
 EXPERIMENT
EXPERIMENT
|
In deze filmpjes zie je twee keer een condensator ontladen. In het eerste filmpje zie je dat een condensator langzaam ontlaad over een led. De led gaat hierdoor langzaam minder fel branden. In het tweede filmpje wordt een condensator kortgesloten. Hierbij is een licht zichtbaar en is een knal te horen.
 DEMO-VIDEO:
Condensator ontladen I
DEMO-VIDEO:
Condensator ontladen I
 DEMO-VIDEO:
Condensator ontladen II
DEMO-VIDEO:
Condensator ontladen II
|
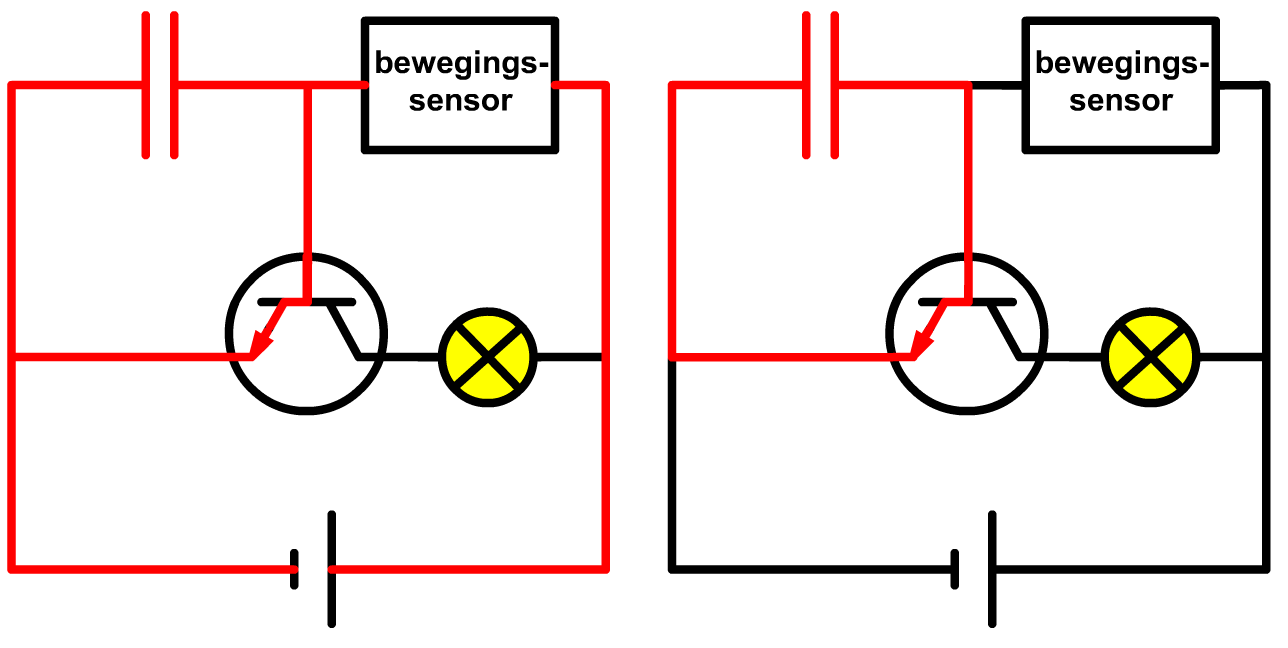
Hieronder is een condensator gecombineerd met een bewegingssensor. Deze sensoren worden bijvoorbeeld gebruikt in tuinen. Als er beweging wordt gedetecteerd in de tuin, dan gaat de lamp aan. Als er geen beweging meer wordt gedetecteerd, dan blijft de lamp een paar seconden branden en daarna gaat de lamp weer uit. Dit werkt als volgt. In de linker onderstaande schakeling wordt beweging gedetecteerd. Hierdoor is de weerstand van de bewegingssensor laag en gaat er een stroom doorheen lopen. Als gevolg gaat de transistor open (en hierdoor gaat de lamp aan) en wordt de condensator opgeladen. Als er dan plots geen beweging meer wordt gedetecteerd, dan gaat de weerstand van de sensor omhoog en kan er geen stroom meer doorheen lopen (zie de rechter afbeelding). Normaalgesproken zou hierdoor de lamp meteen uitgaan, maar omdat de condensator nog even tijd nodig heeft om te ontladen over de B-ingang van de transistor, blijft de transistor open en hierdoor blijft de lamp toch nog even branden.
 Leerdoelen:
Leerdoelen:
|
- Zorg dat je weet dat een NTC een weerstand is waarvan de waarde afneemt bij hogere temperatuur. Bij een PTC neemt de weerstand juist toe bij hogere temperatuur. Bij een LDR neemt de weerstand af als er meer licht op dit onderdeel valt.
- Zorg dat je weet dat een transistor stroom doorlaat van de collector (C) naar de emitter (E) als er stroom door de basis (B) loopt. Zorg ook dat je de werking van schakelingen begrijpt waarbij je een transistor combineert met een ander onderdeel, zoals een NTC of een LDR.
- Zorg dat je weet hoe een condensator opgeladen en ontladen kan worden. Zorg ook dat je weet dat een condensator langzamer leegloopt over een hogere weerstand. Je kan een condensator gebruiken als je in één keer veel energie nodig hebt (bijvoorbeeld bij een flits van een camera) of als je wilt dat een onderdeel langer aanblijft (bijvoorbeeld bij een lamp met bewegingssensor).
|
 Opdrachten
Opdrachten
|
-
(2p) De vloerverwarming in een huis wordt ingeschakeld met een thermostaat. In de thermostaat zit een NTC. Als de temperatuur daalt, neemt de weerstand van de NTC af / toe en neemt de stroomsterkte door de NTC af / toe.
-
(1p) Vul de zin aan: als er stroom loopt door de C / B / E aansluiting van een transistor, dan kan er een stroom lopen van de C / B / E aansluiting naar de C / B / E aansluiting.
-
In de onderstaande afbeelding is tweemaal een schakeling weergegeven waarbij een lamp automatisch aan gaat als het donker wordt.
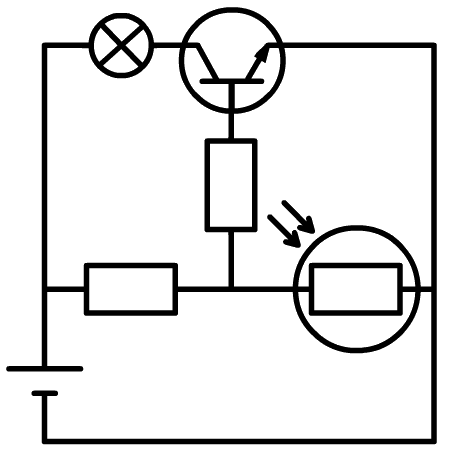 
- (1p) Is de weerstand van de LDR hoger of lager in het donker?
- (1p) Teken in de linker afbeelding hoe de stroom loopt die door de linker weerstand stroomt als er licht op de LDR valt.
- (1p) Teken in de rechter afbeelding hoe de stroom loopt die door de linker weerstand stroomt als het donker is.
- (1p) Leg met behulp van de werking van de transistor uit waarom in dit geval de lamp aangaat.
-
Een lamp bestaat uit 10 identieke leds (zie de rechter schakeling). In de lamp zit een lichtsensor die uit een LDR bestaat. Als het licht is, zijn de leds uitgeschakeld. Als het donker wordt, worden de leds automatisch ingeschakeld.
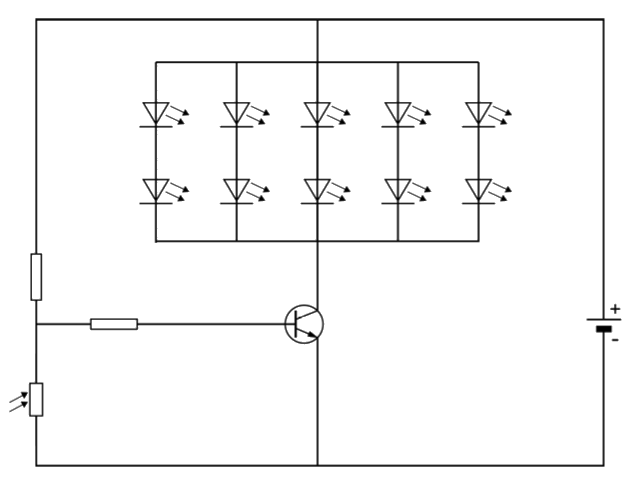
- (4p) Als het donker wordt neemt de weerstand van de LDR af / toe, neemt de stroomsterkte door de LDR af / toe, neemt de stroomsterkte naar de basis van de transistor af / toe en neemt de stroomsterkte van de collector naar de emitter af / toe.
- (1p) Een van de tien leds gaat kapot. Hoeveel leds geven dan licht als het donker wordt?
(Bron: Examen VMBO-T, 2023-1)
-
(2p) Tijdens een natuurkundeles bouwt een leerling een lichtgevoelige schakeling. De leerling wil de schakeling zo maken, dat de led gaat branden als de LDR een grote weerstand heeft. Welk schakelschema is hiervoor geschikt? Leg je antwoord uit.
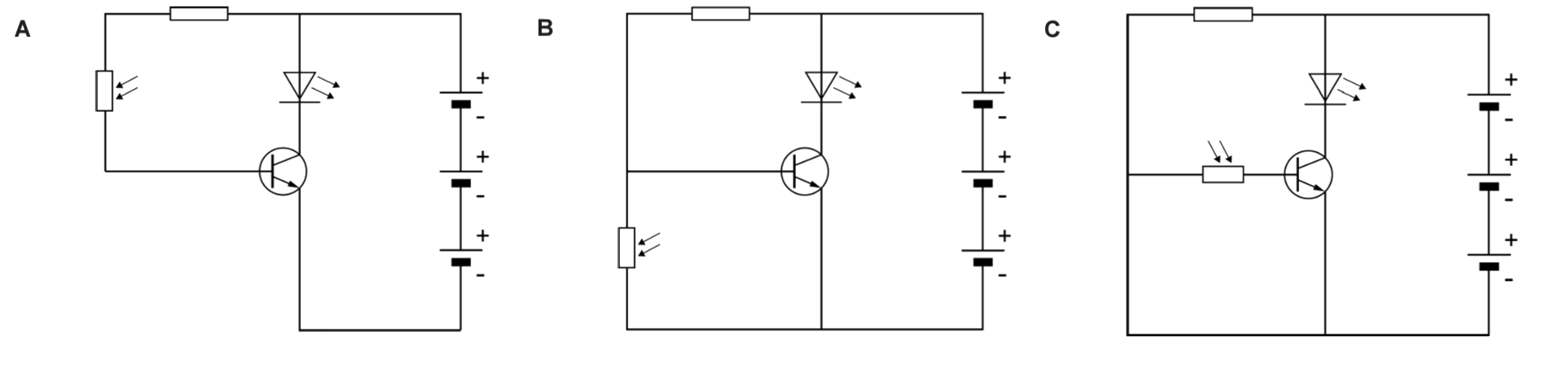
(Bron: Examen VMBO-T, 2022-1)
-
In de onderstaande afbeelding is de schakeling van een flits van een camera weergegeven. We zien eerst de schakeling tijdens het opladen, dan zien we de schakeling waarbij de condensator opgeladen is en daarna zien we de schakeling waarbij de condensator ontladen wordt.
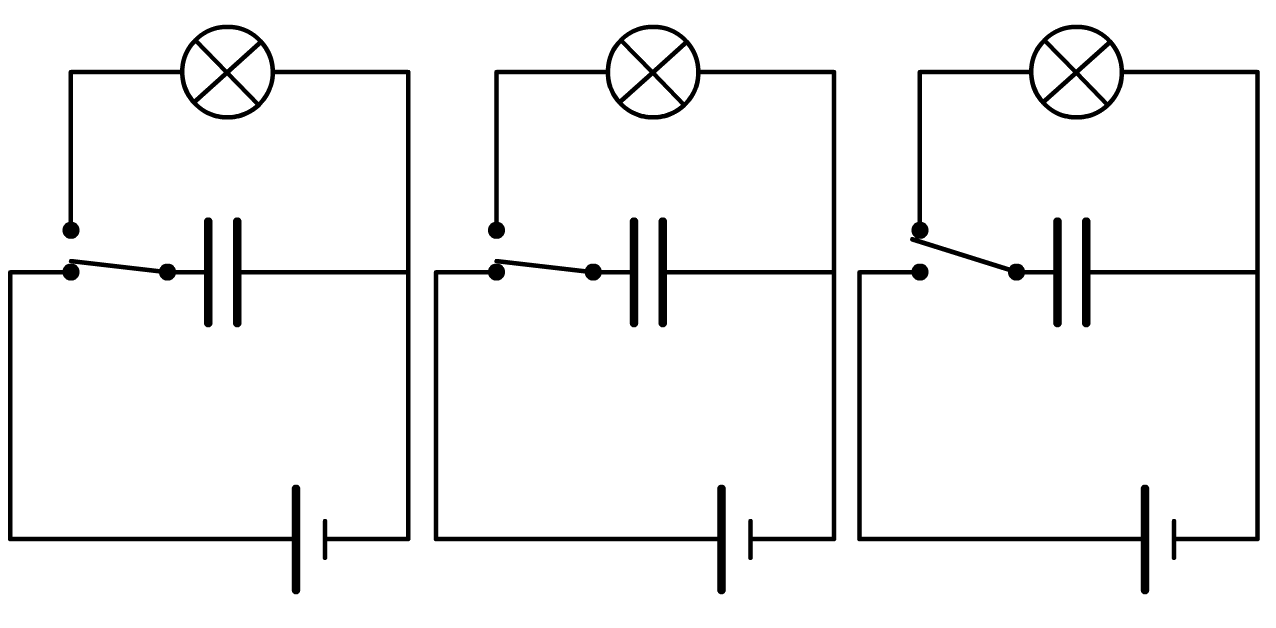
- (1p) Waarom is voor de flits een condensator nodig?
- (3p) Teken in elk van de schakelingen de stroom die door de schakeling loopt.
-
Een leerling voert een practicum uit met een weerstand en een condensator. Je ziet een afbeelding van het schakelschema dat hij gebruikt.
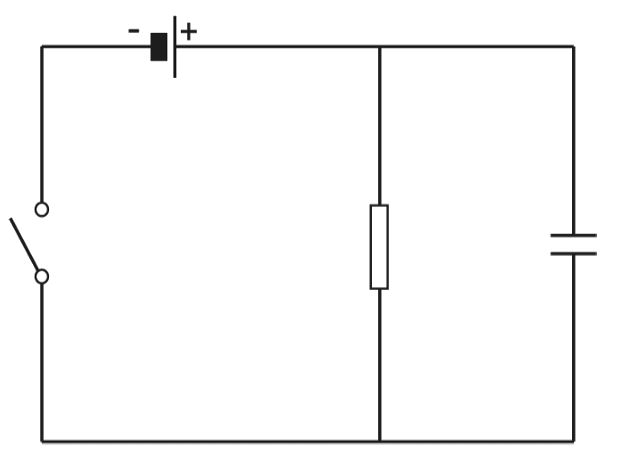
De leerling sluit de schakelaar. Er loopt dan een stroom naar de weerstand en de condensator. De condensator laadt op.
- (2p) Na het sluiten van de schakelaar is de condensator opgeladen. De stroomsterkte door de batterij is dan gelijk / groter dan / kleiner dan die door de weerstand. Leg je antwoord uit.
- (2p) De leerling opent de schakelaar. Geef in de schakeling met pijlen aan, hoe de stroom dan van de condensator door de weerstand loopt.
-
(1p) De leerling meet hoe de spanning over de condensator verandert tijdens het ontladen. Teken het schakelschema inclusief de spanningsmeter.
-
(3p) In de onderstaande tabel zijn de metingen van de leerling weergegeven:
| t(s) | U(V) |
| 0 | 4,5 |
| 50 | 2,6 |
| 100 | 1,4 |
| 150 | 0,7 |
| 200 | 0,3 |
| 250 | 0,1 |
| 300 | 0,0 |
Zet in het onderstaande diagram alle meetpunten uit en teken de grafiek.
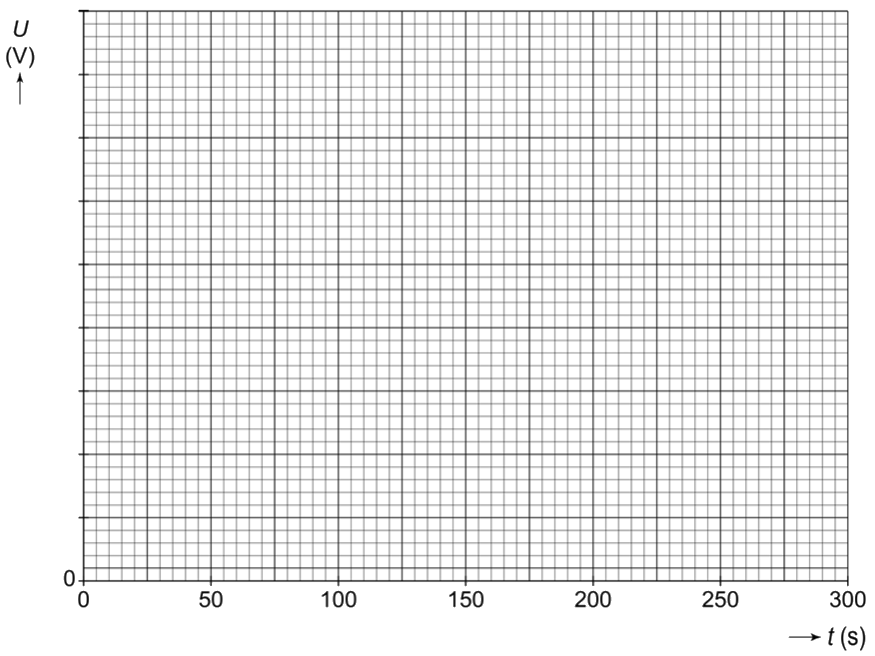
-
(1p) Bepaal de tijd waarna de condensator nog 50% van de beginspanning heeft.
(Bron: Examen VMBO-T, 2021-2)
|
§4 De spoel
In deze paragraaf bespreken we de spoel. Hiermee kunnen we een magneetveld opwekken.
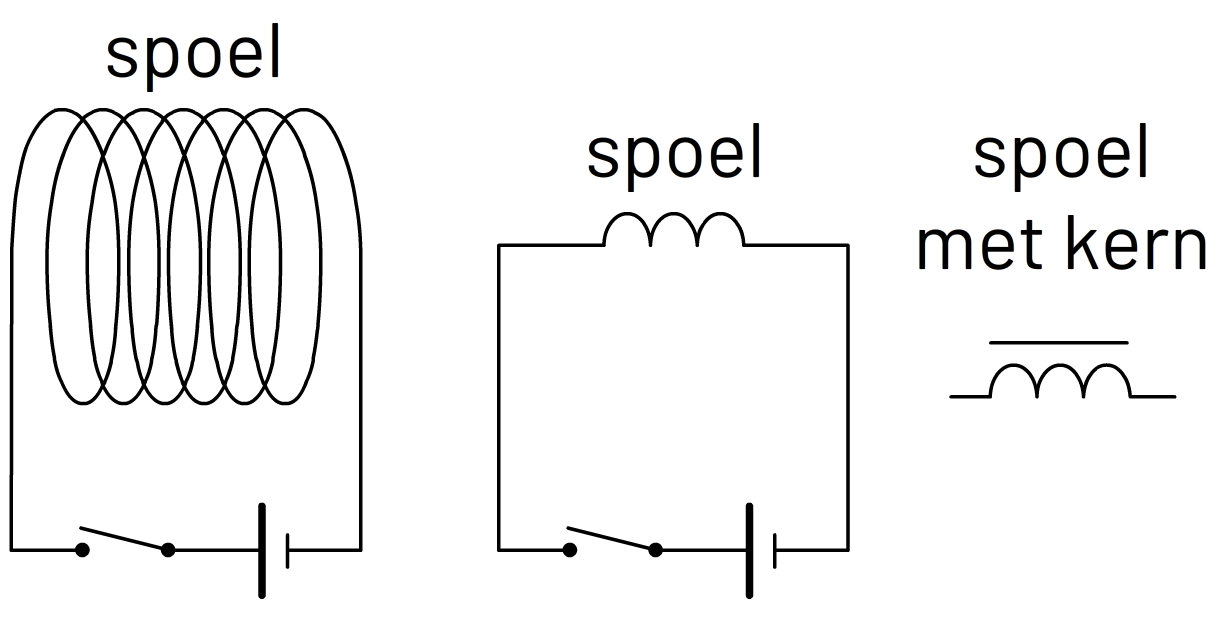
Elke stroomvoerende draad produceert om zich heen een magneetveld. Dit magneetveld kan versterkt worden door een draad heel vaak om te wikkelen tot een spoel (zie de onderstaande linker afbeelding). Omdat spoelen sterke magneetvelden kunnen produceren, noemen we ze ook wel elektromagneten. In de middelste afbeelding is de spoel opgenomen in een schakeling. Als de schakelaar wordt ingedrukt, dan verschijnt het magneetveld rondom de spoel. Als de schakelaar weer open gaat, dan verdwijnt het magneetveld weer. Rechts zien we het symbool voor een spoel. Ook zien we het symbool voor een spoel met een weekijzeren kern. Dit is een stuk ijzer dat in de spoel geplaatst wordt, waardoor het magneetveld sterker wordt.

In de onderstaande afbeelding is het magneetveld afgebeeld dat om een spoel ontstaat. Zo'n veld wordt weergegeven met zogenaamde veldlijnen. Hoe dichter de veldlijnen bij elkaar zitten, hoe sterker het veld. De kant van de spoel waar de veldlijnen uitsteken noemen we de noordpool (N) van de elektromagneet. De kant waar de veldlijnen insteken noemen we de zuidpool (Z) van de elektromagneet. De richting van het magneetveld keert om als we de spoel andersom aansluiten of als we de plus- en de minpool van de spanningsbron omdraaien.
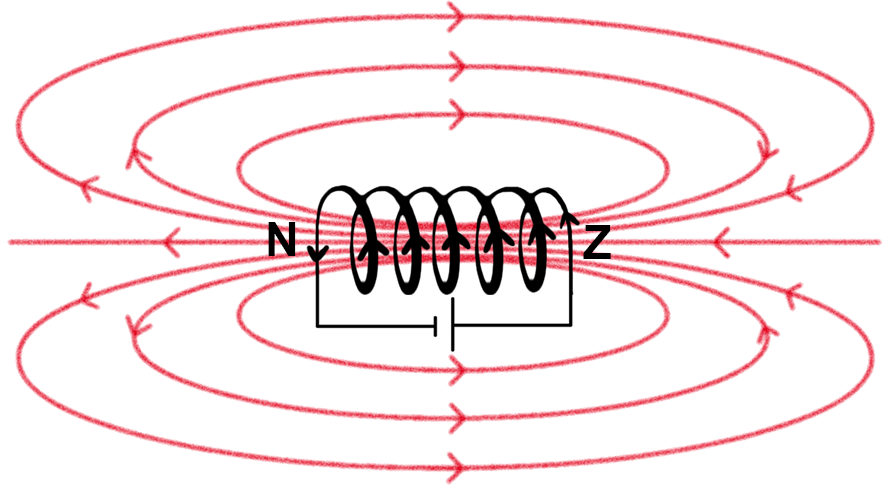
Een magneetveld kan zichtbaar gemaakt worden door ijzervijlsel (kleine stukjes ijzer) rond een magneet te strooien. Dit is te zien in de onderstaande afbeelding. Hier is ijzervijlsel rond een zogenaamde permanente magneet gestrooid. Deze stukjes ijzer gaan zich dan gedragen als kleine kompasjes die in de richting van de veldlijnen wijzen. Merk op dat je hier een magneetveld van dezelfde vorm ziet ontstaan als bij de spoel.

 EXPERIMENT
EXPERIMENT
|
In deze filmpjes zie je het magneetveld om een spoel en om een permanente magneet. Het magneetveld wordt zichtbaar gemaakt met kleine stukjes ijzer (ijzervijlsel) die als kompasnaaldjes in het richting van het magneetveld wijzen.
 DEMO-VIDEO:
Magneetveld van een spoel
DEMO-VIDEO:
Magneetveld van een spoel
 DEMO-VIDEO:
Magneetveld van een permanente magneet
DEMO-VIDEO:
Magneetveld van een permanente magneet
|
 EXPERIMENT
EXPERIMENT
|
|
In het rechter filmpje zie je een zelfgemaakte elektromagneet. Zoals je kan zien kan je hiermee stukjes ijzer aantrekken.
|
 DEMO-VIDEO:
Elektromagneet maken
DEMO-VIDEO:
Elektromagneet maken
|
|
Hieronder zijn een aantal kompasjes afgebeeld rond een permanente magneet. Merk dat de noordpool van de kompasnaaldjes in alle gevallen in de richting van de veldlijnen wijst.
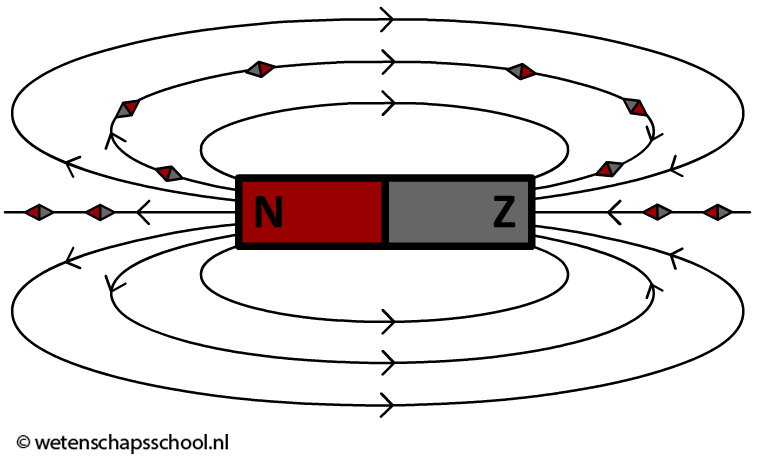
Als we een kompas niet in de buurt van een magneet houden, dan wijst het kompas automatisch richting de Noordpool van de aarde. De aarde zelf produceert namelijk ook een magneetveld. Omdat kompassen op aarde naar de Noordpool wijzen worden ze geregeld gebruikt om de weg te vinden.
Voor zowel elektromagneten als permanente magneten geldt dat twee noordpolen en twee zuidpolen elkaar afstoten en een noord- en een zuidpool elkaar aantrekken (zie de onderstaande afbeelding).
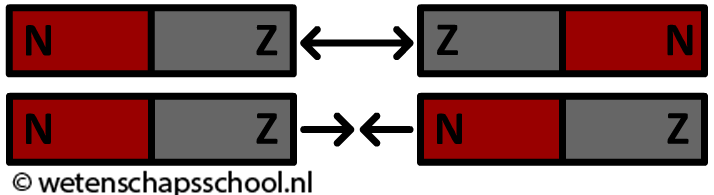
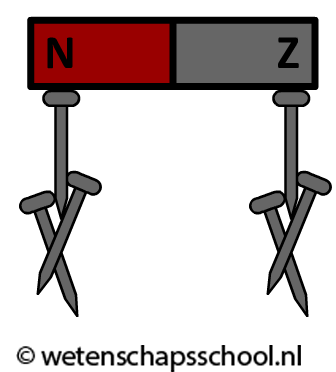
Beide soorten magneten hebben ook de eigenschap dat ze de metalen ijzer en nikkel aantrekken (zie de onderstaande afbeelding). IJzer en nikkel wordt aangetrokken tot zowel de noord- als de zuidpool. Dit komt doordat voorwerpen van ijzer en nikkel in de buurt van een magneet zelf ook tijdelijk magnetisch worden. Ook de onderstaande spijkers in de afbeeldingen worden dus kleine magneten. De spijkers kunnen als gevolg ook weer andere ijzeren spijkers aantrekken.
 EXPERIMENT
EXPERIMENT
|
|
In het rechter filmpje zien we dat een magneet spijkers aantrekt. De spijkers worden hierdoor zelf ook magnetisch en trekken weer andere spijkers aan.
|
 DEMO-VIDEO:
Een magneet met spijkers
DEMO-VIDEO:
Een magneet met spijkers
|
|
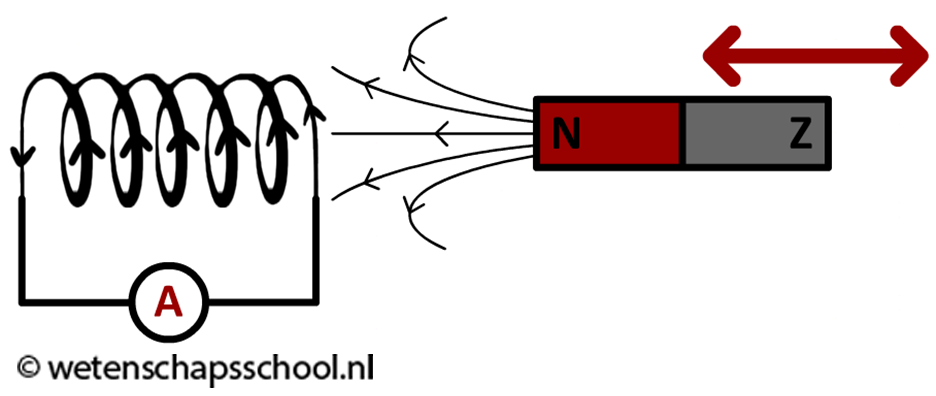
Als we een magneet bewegen in de buurt van een spoel of een spoel bewegen in de buurt van een magneet, dan ontstaat er een spanning over de spoel. Bij een gesloten stroomkring gaat er dan ook een stroom lopen door de spoel. We zien dit in de volgende afbeelding. Door een magneet te bewegen bij een spoel kan je een stroompje produceren dat je o.a. met een ampèremeter kan detecteren.
 Demonstratievideo
Demonstratievideo
|
|
In de rechter video is dit effect te zien. Twee tegengesteld gerichte LED-lampen zijn aangesloten op de spoel. Zo is te zien dat de stroomrichting afhangt van of we de magneet richting de spoel of juist van de spoel af bewegen.
|
 DEMO-VIDEO:
Inductie
DEMO-VIDEO:
Inductie
|
|
Op deze manier kan je dus stroom opwekken. Dit is o.a. hoe een dynamo werkt. Dynamo's worden soms gebruikt om fietslampen aan te drijven. Hieronder zien we een voorbeeld. Een magneet is aan een wiel verbonden en beweegt telkens langs een spoel in de dynamo. Op deze manier wordt stroom opgewekt en gaat de lamp branden.

Een grote versie van een dynamo wordt een generator genoemd. Er zit bijvoorbeeld een generator in een windmolen. Wind zorgt dat de grote wieken van de windmolen gaan draaien en daarmee wordt in de generator een grote spoel rondgedraaid in de buurt van magneten (of andersom), waardoor elektriciteit wordt opgewerkt.
Twee andere elektrische componenten waarbij magnetisme wordt gebruikt zijn het reedcontact (spreek dit op z'n Engels uit als "read") en het relais (spreek dit op z'n Frans uit). Hieronder zien we links een foto van een reedcontact en rechts zien we de bijbehorende symbolen. Een reedcontact werkt als volgt. Het bestaat uit twee stukjes metaal die normaalgesproken geen contact maken, behalve als we een magneet in de buurt houden.

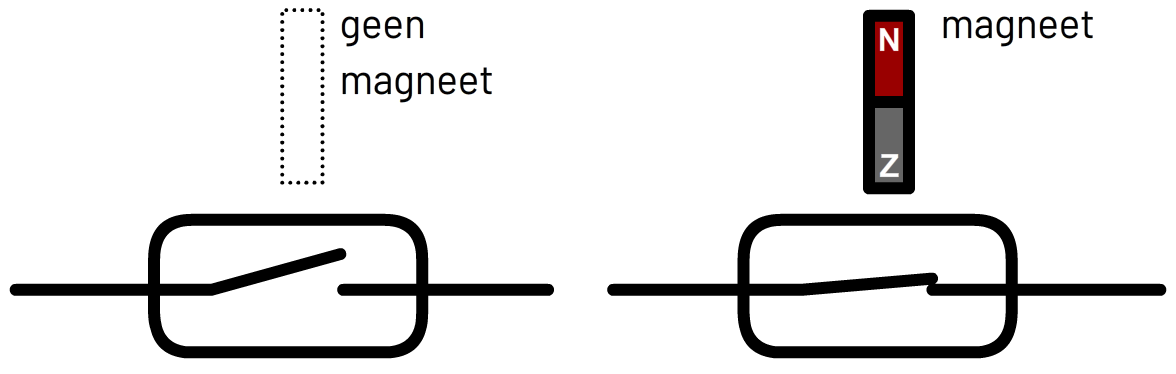
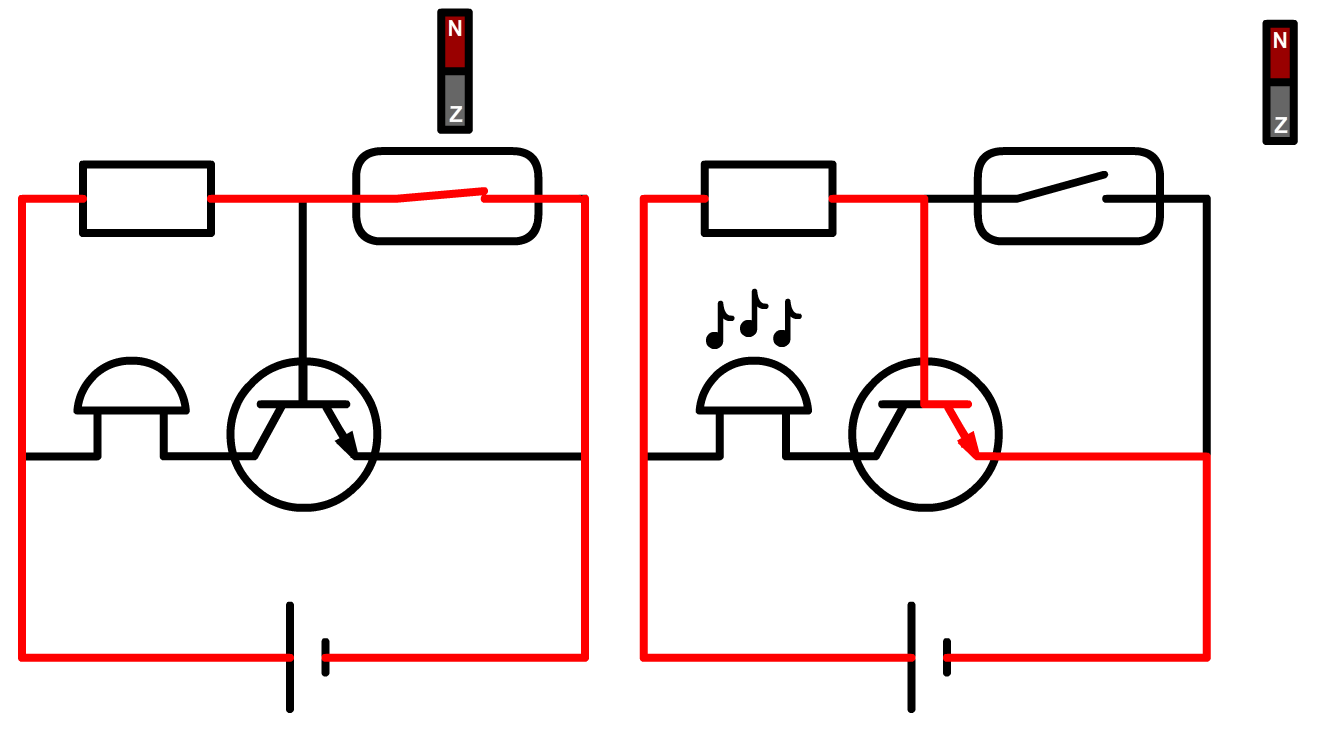
Er zit bijvoorbeeld een reedcontact in inbrekersalarmen die op deuren en ramen aangesloten kan worden (zie de linker onderstaande foto). Als de deur of het raam opengaat, dan beweegt de magneet weg van het reedcontact. Hierdoor wordt de schakeling geopend en gaat het alarm af. De bijbehorende schakeling is rechts weergegeven. Als de magneet bij het reedcontact is (en de deur dus dicht is), dan gaat de meeste stroom door het reedcontact en gaat de transistor niet open. Als de magneet weggehaald wordt, dan gaat er wel een stroom lopen door de B-ingang van de transistor en gaat het alarm af.

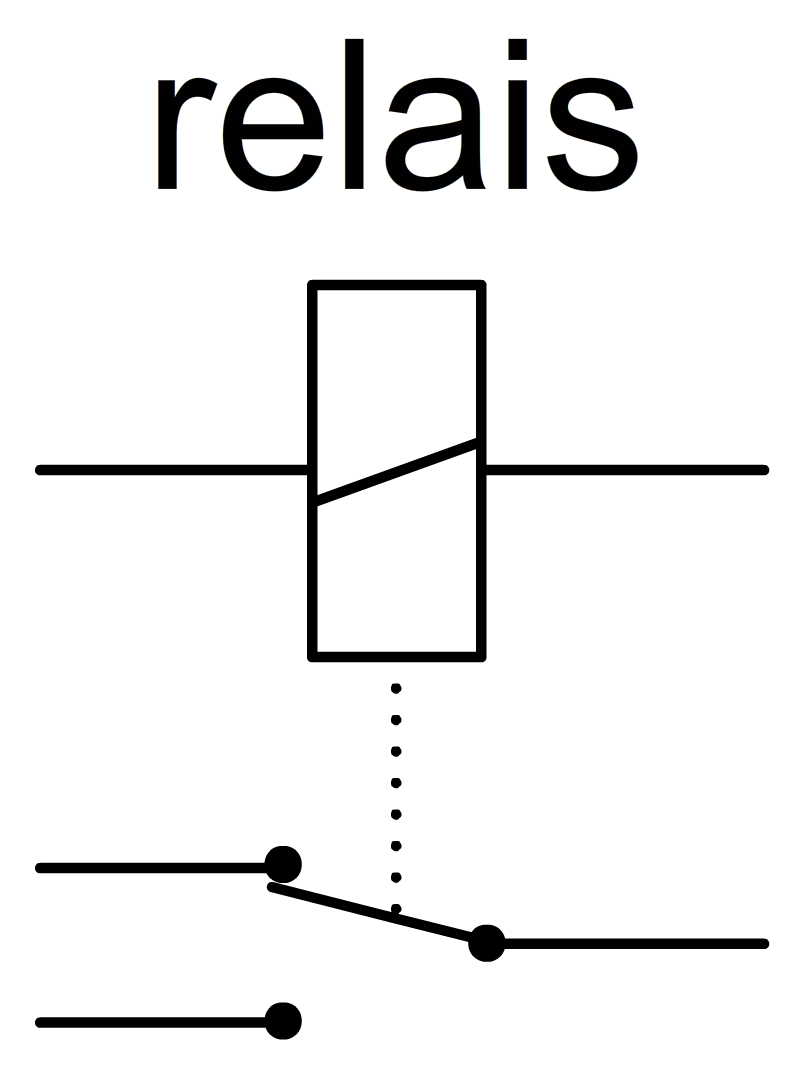
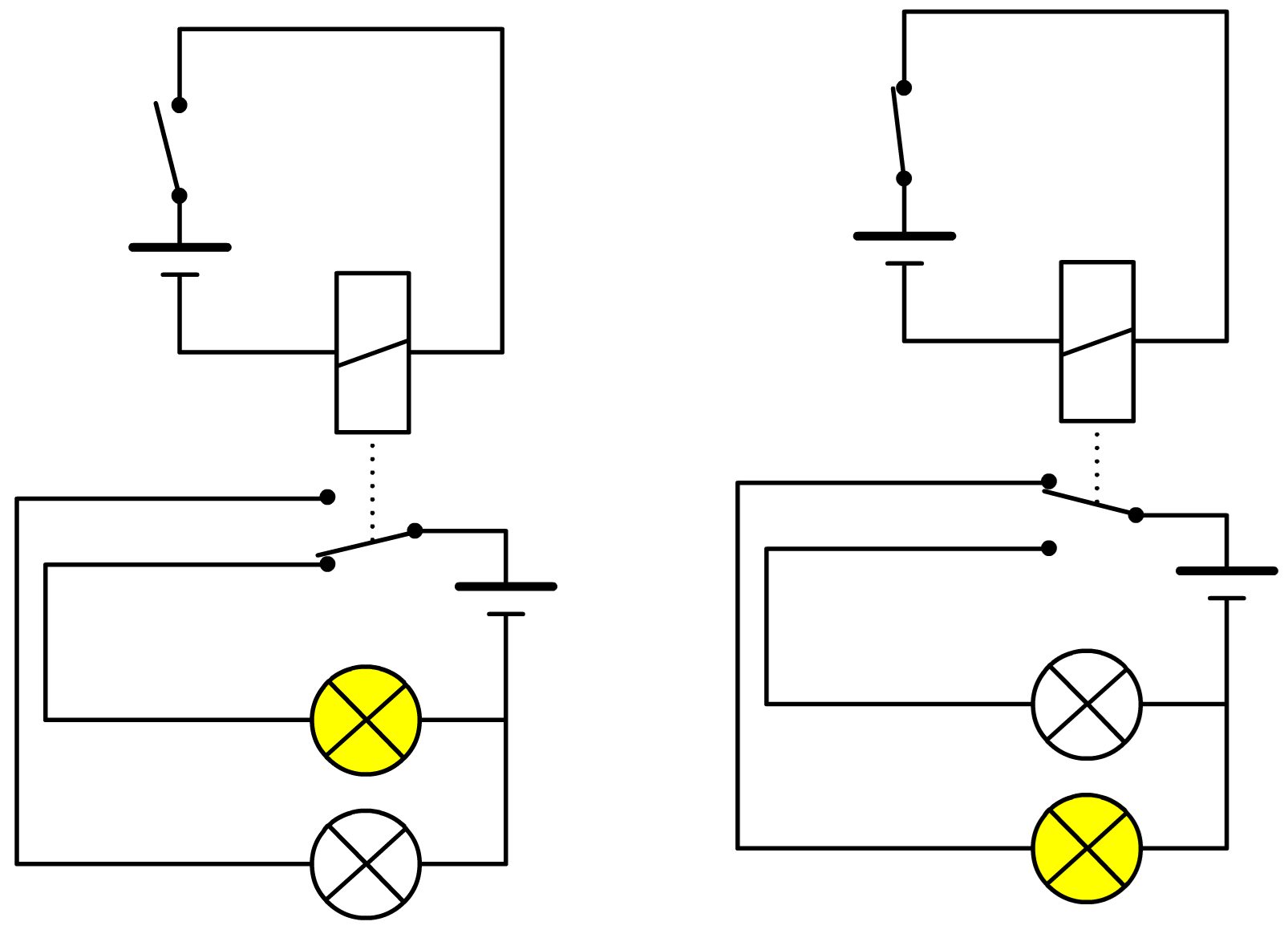
Dan hebben we nog het relais (zie de linker afbeelding). Een relais is een automatische schakelaar die werkt met een elektromagneet. We zien de werking in de rechter twee schakelingen. Als de bovenstaande stroomkring gesloten wordt (rechts), dan zorgt het relais dat een schakelaar in de onderste schakeling omgaat.
 Leerdoelen:
Leerdoelen:
|
- Zorg dat je weet dat een stroomvoerende draad een magneetveld produceert en dat dit versterkt wordt als je de draad wikkelt tot een spoel, met name als de spoel een weekijzeren kern heeft. We noemen een spoel daarom ook wel een elektromagneet.
- Zorg dat je weet dat de magneetveldlijnen uit de noordkant van de elektromagneet steken en in de zuidkant van de elektromagneet steken. Zorg ook dat je weet dat ijzervijlsel en kompassen in de richting van de veldlijnen wijzen.
- Zorg dat je weet dat gelijke polen van permanente magneten of elektromagneten elkaar afstoten en dat verschillende polen elkaar aantrekken.
- Zorg dat je weet dat ijzer en nikkel worden aangetrokken door zowel de noord- als de zuidpool van magneten. Andere metalen worden niet aangetrokken.
- Zorg dat je weet dat het bewegen van een magneet in de buurt van een spoel ervoor zorgt dat er stroom wordt opgewekt in de spoel. Bij een generator en een dynamo wordt op deze manier elektriciteit opgewekt met een spoel en een magneet.
- Zorg dat je weet dat een reedcontact een schakelaar is die sluit als een magneet in de buurt is. Zorg ook dat je weet dat een relais een schakelaar is die met een elektromagneet aan- en uitgezet kan worden.
|
 Opdrachten
Opdrachten
|
-
(2p) Teken het symbool voor een spoel, een spoel met kern, een relais en een reedcontact.
-
(1p) De noordpolen van twee magneten stoten elkaar af / trekken elkaar aan.
-
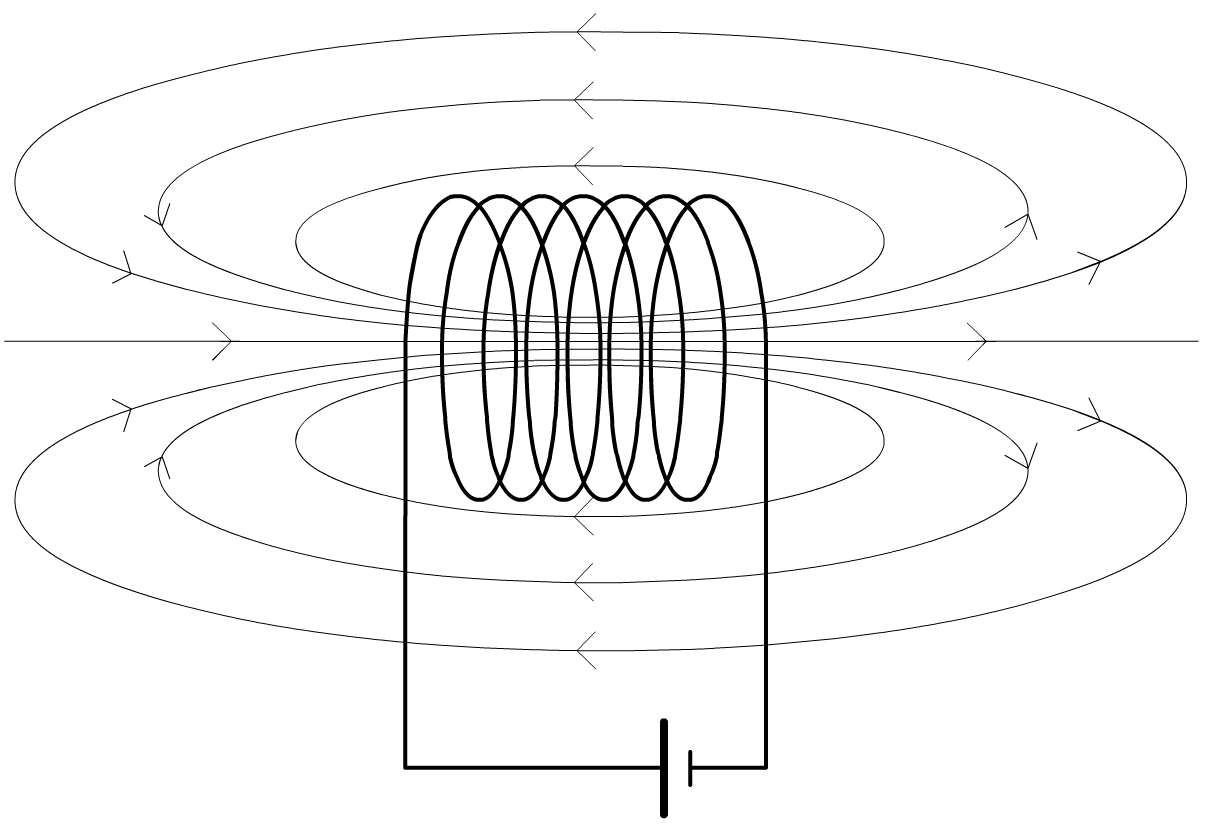
(1p) Teken een N voor de noordpool en een Z voor de zuidpool op de juiste plaats in de onderstaande afbeelding:
-
(1p) Wat gebeurt er als je een magneet heen en weer beweegt in de buurt van een spoel.
-
In een wijk wordt veel ingebroken. Bij de inbraken worden vaak ramen op de benedenverdieping geforceerd. Om dit te voorkomen wordt een inbrekersalarminstallatie op de ramen aangesloten. Op het raam zelf wordt een magneet geplakt en op het raamkozijn een sensor met een reedcontact.
- (1p) Beschrijf de werking van het reedcontact.
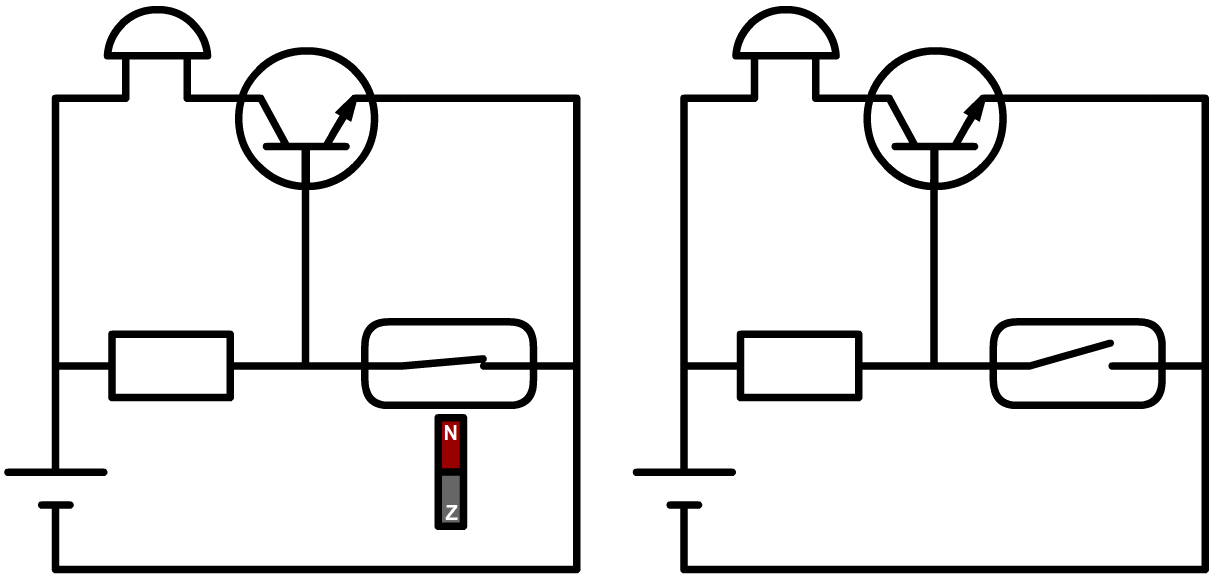
- (2p) Hieronder is de bijbehorende schakeling weergegeven.
Teken hoe de stroom loopt als de magneet zich in de buurt van het reedcontact bevindt. Leg ook uit of het alarm nu af gaat.
-
(2p) Teken hoe de stroom loopt als de magneet bij het openen van het raam verwijderd wordt van het reedcontact. Leg ook uit of het alarm nu af gaat.
-
Een automotor wordt gestart met een startmotor. De startmotor is een elektromotor die zijn energie krijgt van een accu. Als de sleutel in het contactslot wordt omgedraaid, schakelt een relais de startmotor in. Je ziet hier een vereenvoudigd schakelschema. De weerstand van de startmotor is veel kleiner dan de weerstand van de spoel van het relais.
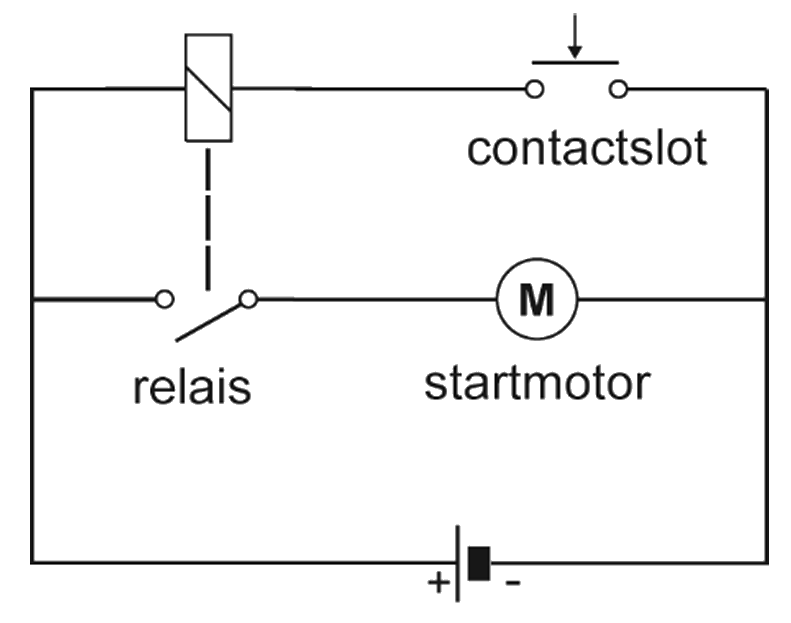
- (1p) Leg uit wat er gebeurt als de sleutel in het contactslot omdraait.
-
(1p) Wat is een voordeel van het gebruik van een relais in deze schakeling? Kies uit:
- Zodat de startmotor snel aangezet kan worden.
- Zodat de weerstand van de schakeling niet te groot wordt, waardoor de startmotor niet goed werkt.
- Zodat er geen grote stroom door het contactslot stroomt.
(Bron: Examen VMBO-KB, 2022-1)
-
Een leerling hangt een metalen blokje (74 g) aan een veer en trekt dit blokje daarna naar beneden met een elektromagneet die is aangesloten op een variabele spanningsbron.

- (1p) Van welke twee materialen kan het blokje gemaakt zijn?
- (2p) Wat gebeurt er met het magneetveld als de spoel wordt omgedraaid? En wat gebeurt er dan met het blokje? Wordt het nu aangetrokken of afgestoten.
- (1p) In de onderstaande afbeeldingen is de elektromagneet weergegeven met twee veldlijnen. In welke afbeeldingen zijn de veldlijnen juist getekend?
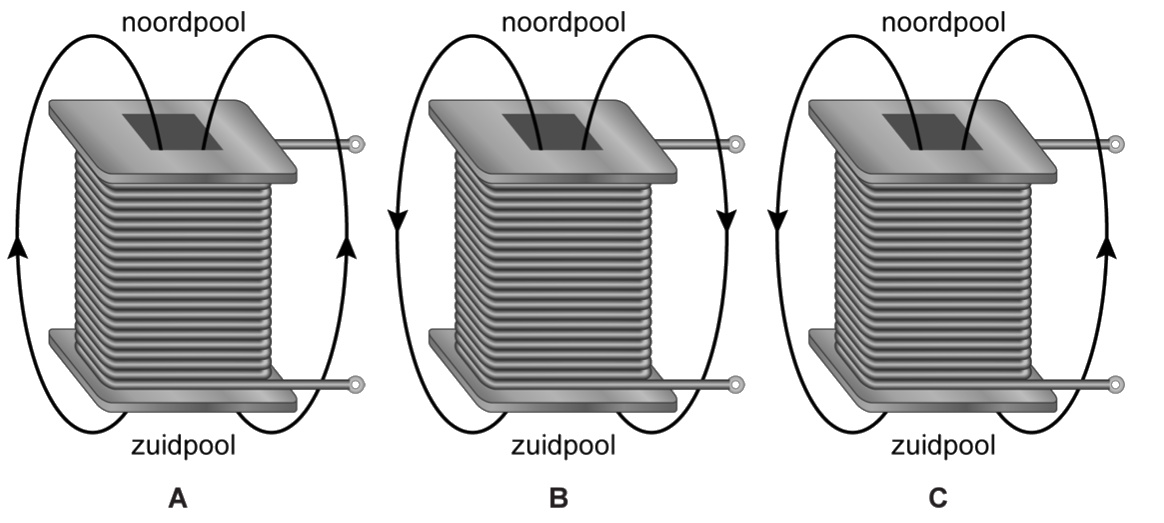
-
(3p) De leerling meet de spanning over en de stroomsterkte door de spoel. Teken het schakelschema met stroommeter, spanningsmeter en de spoel met kern.
(Bron: Examen VMBO-T, 2023-1)
-
Aan de achterkant van een lamp zit een magneet. De lamp wordt daarmee aan een koelkast bevestigd.
- (1p) De deur van de koelkast is van staal gemaakt. Leg uit dat de magneet hiertoe aangetrokken wordt.
-
(1p) Hieronder is de zijkant van de lamp en de magneet te zien. De noordpool is aangegeven met de letter N. Welke magnetische pool is te vinden bij 1 en bij 2?
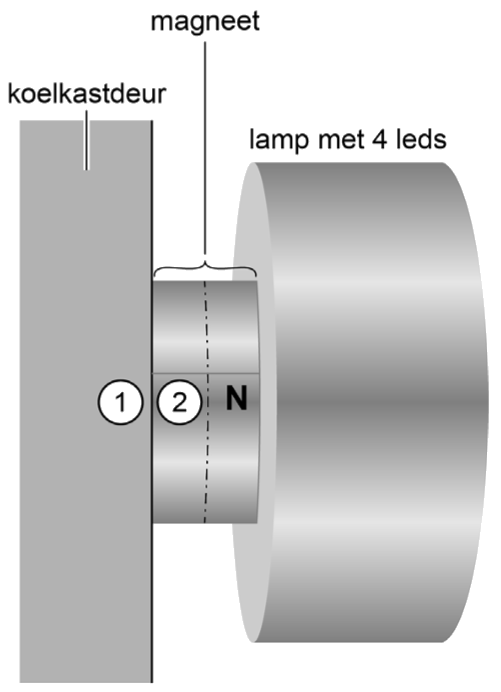
(Bron: Examen VMBO-T, 2023-2)
-
Een kleine windturbine levert elektrische energie aan verkeerslichten. De windturbine wekt elektrische energie op met behulp van een dynamo.
- (1p) Leg uit hoe de dynamo van een windturbine elektriciteit opwekt.
-
(1p) Noteer de twee onderdelen in een dynamo die nodig zijn om elektrische energie op te wekken.
(Bron: Examen VMBO-T, 2022-2)
-
Een leerling hangt een ijzeren blokje aan een newtonmeter. Onder het blokje plaats de leerling een elektromagneet. De leerling bepaalt de magnetische kracht op het blokje bij verschillende afgegeven vermogens van de spanningsbron en de magnetische kracht op het blokje. De resultaten zijn hieronder weergegeven:
| Vermogen (W) | Kracht (N) |
| 2,0 | 0,01 |
| 3,6 | 0,02 |
| 5,8 | 0,04 |
| 6,6 | 0,05 |
| 8,0 | 0,07 |
- (3p) Teken de bijbehorende grafiek in het onderstaande diagram:
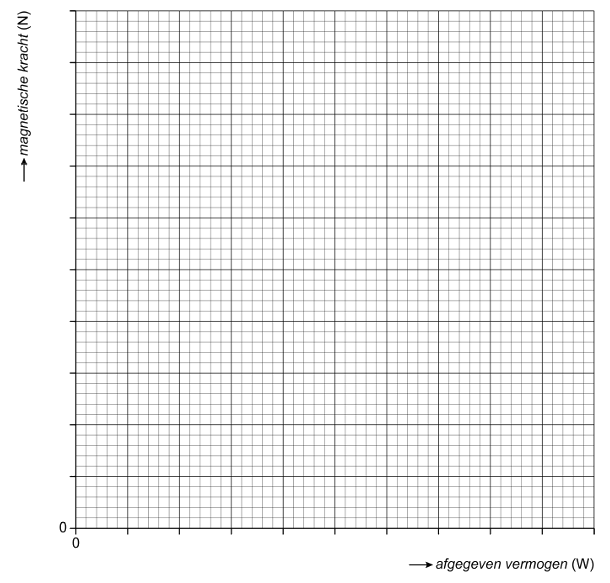
-
(1p) Wat is juist over het afgegeven vermogen van de spanningsbron als de magnetische kracht op het blokje twee keer zo groot wordt? Kies uit:
- Het afgegeven vermogen is minder dan twee keer zo groot
- Het afgegeven vermogen is twee keer zo groot
- Het afgegeven vermogen is meer dan twee keer zo groot.
-
(2p) De leerling zet de spanningsbron uit. Het blokje gaat daardoor wat hoger hangen. Daarna wisselt ze de plus en de min van de spanningsbron. Wat gebeurt er nu met het blokje als de leerling de spanningsbron weer aan zet. Kies uit:
- Het blokje blijft stil hangen
- Het blokje wordt aangetrokken
- het blokje wordt afgestoten.
Leg je antwoord uit.
(Bron: Examen VMBO-T, 2023-1)
-
Een leerling gaat na of tuinaarde een geleider kan zijn voor elektrische stroom. Je ziet een afbeelding van de schakeling die hij gebruikt. Twee koperen plaatjes zijn in een pot met tuinaarde gestoken.

- (1p) De koperen plaatjes raken de bodem van de pot. Waarom is het belangrijk dat de pot niet van metaal is gemaakt?
- (2p) Teken het schakelschema. Voeg een accu, een schakelaar en een spoel met kern toe. Gebruik voor de pot met tuinaarde een rechthoek met het woord "tuinaarde" erin.
-
(1p) De schakelaar staat open. De leerling zet een kompasnaald op een voet naast de spoel. De leerling geeft de kompasnaald een zetje. De naald draait een paar keer rond en blijft dan in een stand stilstaan. Geeft hij de naald weer een zetje, dan komt deze weer in dezelfde stand tot stilstand. Waarom gaat de kompasnaald in deze stand staan?
-
(2p) De leerling drukt de schakelaar in. De stand van de kompasnaald verandert hierdoor niet. Dan giet de leerling een beetje kraanwater op de droge tuinaarde. Op een gegeven moment draait een punt van de kompasnaald naar het uiteinde van de spoel.
Het toevoegen van kraanwater heeft gevolgen voor de weerstand van en de stroomsterkte door de tuinaarde. De weerstand wordt hierdoor groter / kleiner. De stroomsterkte wordt hierdoor groter / kleiner.
-
(1p) Leg uit waarom de kompasnaald in een andere stand gaat staan.
-
Bekijk de onderstaande foto. Het uiteinde van de kompasnaald (1) is een noordpool. Geef aan wat punt 2 en 3 zijn.

-
(3p) De leerling wil de kompasnaald de andere kant op laten wijzen. Hij wisselt daarvoor de aansluitsnoeren bij de accu om en bekijkt het gevolg. Dan zet hij de snoeren weer terug. Deze handelingen herhaalt hij bij de andere drie onderdelen.
Geef bij elk van de onderdelen aan of het omdraaien van het onderdeel zorgt dat de kompasnaald van richting verandert. Doe dit voor de accu, de koperen plaatjes in de aarde, de schakelaar en de spoel.
(Bron: Examen VMBO-T, 2021-2)
|
§5 De transformator
In deze paragraaf introduceren we de transformator. Hiermee kunnen we spanning verhogen of verlagen.
Nu we begrijpen dat een spoel een magneetveld kan opwekken, kunnen we ook de transformator begrijpen. Een transformator werkt door twee spoelen naast elkaar te plaatsen (zie de onderstaande schakeling). De linker schakeling bevat een wisselspanning. Dit is een spanningsbron waarbij de stroomrichting telkens omwisselt. Ook bevat de linker schakeling een spoel, genaamd de primaire spoel. Door het wisselspanning ontstaat in deze spoel een wisselend magneetveld. Het wisselende magneetveld wordt opgevangen door de spoel in de rechter schakeling, de zogenaamde secundaire spoel. Als gevolg hiervan gaat er een stroom lopen door deze spoel. In de onderstaande schakeling gaat hierdoor de lamp branden.
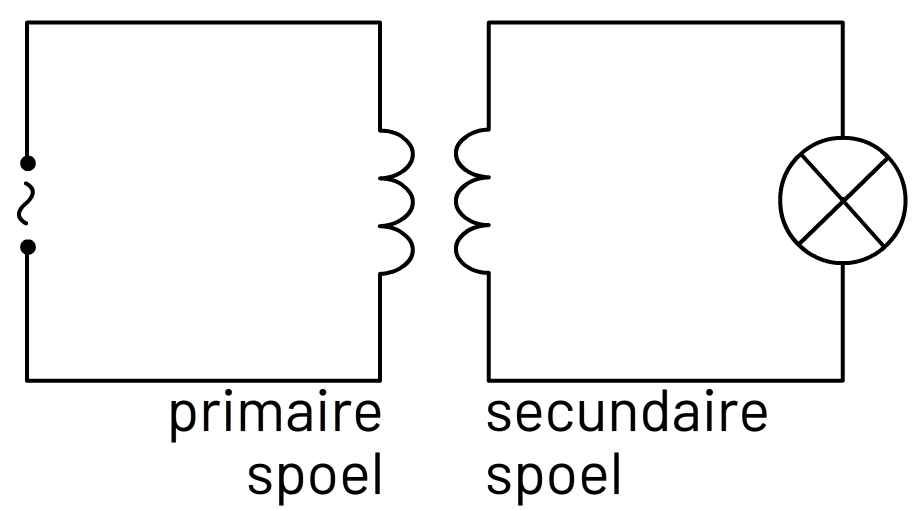
Merk op dat de wisselspanning en de lamp in twee losse schakelingen zitten die niet fysiek met elkaar verbonden zijn. Hier wordt goed gebruik van gemaakt bij bijvoorbeeld het opladen van een elektrische tandenborstel. In de oplader bevindt zich de primaire spoel en in de bodem van de tandenborstel de secundaire spoel. Zowel de bodem van de tandenborstel en de oplader zijn afgesloten met plastic, zodat er geen water bij kan komen. Het magneetveld van de primaire spoel gaat dwars door het plastic heen en zo wordt de tandenborstel veilig opgeladen.

 Demonstratievideo
Demonstratievideo
|
|
In het rechter filmpje wordt dit effect gedemonstreerd. In de tweede helft van het filmpje wordt ook een weekijzeren kern in de spoel gelegd. Dit ijzer wordt door het magneetveld van de spoel gemagnetiseerd, waardoor het veld sterker wordt.
|
|
|
Een transformator kan ook gebruikt worden om de spanning te verhogen of te verlagen. We noemen dit het transformeren van de spanning. Een generator in een elektriciteitscentrale produceert bijvoorbeeld vaak een spanning rond de 10 kV. Als we deze stroom willen transporteren over grote afstanden, bijvoorbeeld via hoogspanningskabels (zie de onderstaande linker afbeelding), dan wordt de spanning eerst omhoog getransformeerd naar 400 kV. Deze hoge spanning zorgt namelijk voor een lager energieverlies in deze kabels. In zogenaamde transformatorhuisjes (zie de rechter afbeelding) wordt de spanning omlaag getransformeerd naar 230 V en deze spanning komt aan bij de huizen.

 (Afbeelding: A. J. van der Wal; CC BY-SA 4.0)
(Afbeelding: A. J. van der Wal; CC BY-SA 4.0)
Deze 230 V is vaak nog te hoog voor een hoop apparaten die we in huis gebruiken. Denk bijvoorbeeld aan je laptop of je telefoon. In dat geval gebruik je een adapter die de spanning nogmaals omlaag transformeert (zie de onderstaande afbeelding). Voor een laptop is dit bijvoorbeeld vaak rond de 20 V.
 (Afbeelding: Evan-Amos; PD)
(Afbeelding: Evan-Amos; PD)
Maar hoe werkt het transformeren eigenlijk? Door het aantal windingen van de spoelen te variëren, kunnen we de spanning over de secundaire spoel aanpassen. Als het aantal windingen van de secundaire spoel bijvoorbeeld twee keer zo klein is als het aantal windingen van de primaire spoel, dan wordt de spanning over de secundaire spoel ook twee keer zo klein (zie de onderstaande afbeelding).
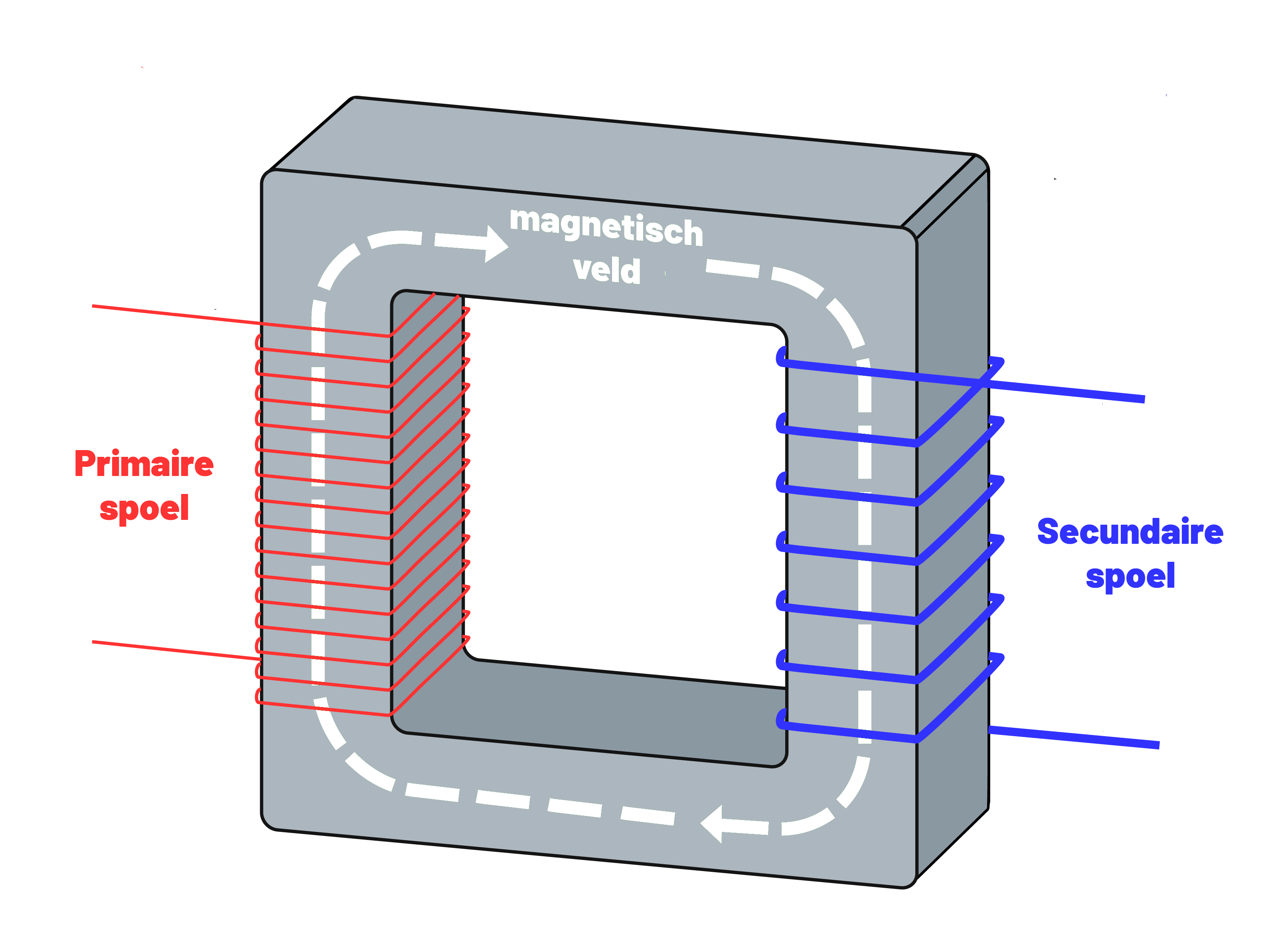 (Afbeelding: BillC; CC BY-SA 3.0)
(Afbeelding: BillC; CC BY-SA 3.0)
In formuletaal kunnen we dit als volgt samenvatten:
$$ \frac{N_p}{N_s} = \frac{U_p}{U_s} $$
| Aantal windingen van primaire spoel (Np) |
- |
| Aantal windingen van secundaire spoel (Ns) |
- |
| Spanning over de primaire spoel (Up) |
volt (V) |
| Spanning over de secundaire spoel (Us) |
volt (V) |
|
"p" staat in deze formule voor de primaire spoel en "s" voor de secundaire spoel. De "N" staat voor het aantal windingen van de spoelen en de "U" voor de spanning over de spoelen.
Een transformator die geen energie verliest noemen we een ideale transformator. Hiervoor geldt:
$$ P_p = P_s \;\;\;\;\; \text{(ideaal)} $$
Dit kunnen we met de formule P = UI uitschrijven tot:
$$ U_p I_p = U_s I_s \;\;\;\;\; \text{(ideaal)} $$
Aan deze formule zien we o.a. dat als de spanning over de primaire spoel groter is, dat dan de stroomsterkte over de secundaire spoel groter is (en andersom).
In werkelijkheid zijn transformatoren nooit volledig ideaal. Er gaat altijd energie verloren in de vorm van warmte. We kunnen het rendement van een transformator wel vergroten door een weekijzeren kern in de spoelen te plaatsen (zie de onderstaande afbeelding). Het ijzer zorgt ervoor dat het magneetveld beter aankomt bij de secundaire spoel.

 Voorbeeld
Voorbeeld
|
|
Vraag:
Hieronder is een laptopadapter afgebeeld die is aangesloten op de netspanning. Geef de primaire en de secundaire spanning over de spoelen in de adapter. Gebruik hiervoor de informatie in de afbeelding.

Antwoord:
De netspanning is in Nederland altijd 230 V. Dit is de spanning over de primaire spoel. In de afbeelding zien we dat de "output" van de adapter 18,5 V is. Dit is de spanning over de secundaire spoel. Er geldt dus:
Up = 230 V
Us = 18,5 V
Vraag:
De primaire spoel heeft 398 windingen. Hoeveel windingen heeft de secundaire spoel.
Antwoord:
Np = 398 windingen
Nu vullen we de formule in:
$$ \frac{N_p}{N_s} = \frac{U_p}{U_s} $$
$$ \frac{398}{N_s} = \frac{230}{18,5} $$
De rechterkant van de vergelijking kunnen we al uitrekenen:
$$ \frac{398}{N_s} = 12,4 $$
Deze formule kunnen we omschrijven:
$$ N_s = \frac{398}{12,4} = 32 \text{ windingen} $$
De secundaire spoel heeft dus 32 windingen.
Vraag:
De stroomsterkte door de secundaire spoel is 3,5 A. Bereken hiermee de stroomsterkte door de primaire spoel. Ga hier uit van een ideale transformator.
Antwoord:
Is = 3,5 A
Voor een ideale transformator geldt:
$$ U_pI_p = U_sI_s $$
$$ 230 \times I_p = 18,5 \times 3,5 $$
De rechterzijde kunnen we nu uitrekenen:
$$ 230 \times I_p = 64,75 $$
De primaire stroomsterkte wordt hiermee:
$$ I_p = 0,28 \text{ A} $$
Vraag:
In werkelijkheid is de transformator natuurlijk niet ideaal. Het vermogen van de primaire spoel is 72 W. Bereken met behulp van de foto het rendement van de adapter.
Antwoord:
De adapter levert volgens de foto een nuttig vermogen van 65 W. Het totale vermogen is 72 W. Er geldt dus:
Pnuttig = 65 W
Ptot = 72 W
Het rendement wordt hiermee:
$$ \eta = \frac{P_{nuttig}}{P_{tot}} $$
$$ \eta = \frac{65}{72} = 0,90 $$
Het rendement is dus 0,90 × 100 = 90%.
|
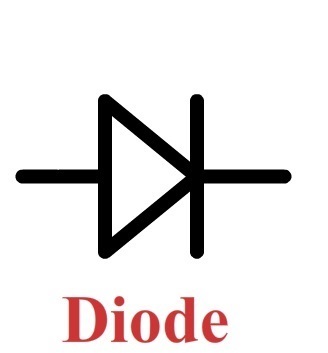
Het laatste onderdeel dat we in deze paragraaf bespreken is de diode (zie de onderstaande afbeelding). Een diode is een onderdeel dat stroom alleen in één richting doorlaat. Het symbool voor een diode is hieronder weergegeven en lijkt een beetje op een pijltje. Stroom kan alleen worden doorgelaten in de richting van dit pijltje. In de opdrachten gaan we zien dat we met een diode wisselspanning kunnen omzetten naar gelijkspanning. Veel apparaten, zoals laptops en telefoons, hebben gelijkspanning nodig om te kunnen functioneren. Hier worden dus diodes voor gebruikt.
Er bestaan ook lichtgevende diodes. Dit worden ook wel leds genoemd. Leds hebben het voordeel dat ze een veel hoger rendement hebben dan bijvoorbeeld gloeilampen. Het nadeel is dat ze stroom maar in één richting doorlaten. Als je de led verkeerd om aansluit, dan brandt hij niet.



 Leerdoelen:
Leerdoelen:
|
- Zorg dat je weet dat je met een transformator spanning omhoog en omlaag kan transformeren aan de hand van het aantal windingen van de primaire en de secundaire spoel. Je kan dit berekenen met de formule "Np/Ns = Up/Us".
- Zorg dat je weet dat bij een ideale transformator geldt dat "Pp = Ps". Dit gaat uit van een rendement van 100%. In de praktijk hebben transformatoren natuurlijk wel energieverlies.
- Zorg dat je weet dat je deze formule ook kan uitschrijven tot "UpIp = UsIs". Deze formule vertelt ons dat als de ene spoel een hogere spanning heeft, dat de andere spoel een hogere stroomsterkte heeft.
- Zorg dat je weet dat een diode stroom alleen in de richting van het "pijltje" doorlaat en dat diodes gebruikt worden om wisselspanning om te zetten in gelijkspanning. Een lichtgevende diode noemen we een LED
|
 Opdrachten
Opdrachten
|
-
Een elektrische geurverspreider is via een adapter op de netspanning aangesloten. De secundaire spoel van de transformator levert een spanning van 12 V. De primaire spoel heeft 1150 windingen.
- (2p) Bereken het aantal windingen van de secundaire spoel.
-
(3p) De stroomsterkte door de secundaire spoel is 80 mA. Bereken hiermee de stroomsterkte door de primaire spoel. Ga ervan uit dat de transformator ideaal is.
(Bron: Examen VMBO-T, 2023-1)
-
Voor het opladen van de accu van een tablet wordt een USB-lader gebruikt die op de netspanning kan worden aangesloten. In de lader zit een transformator. Ga ervan uit dat de transformator ideaal is.

- (2p) Het opgenomen vermogen is 14,5 W. Bereken de stroomsterkte door de primaire spoel.
- (2p) De transformator verlaagt de spanning naar 5,0 V. Bereken het aantal windingen van de secundaire spoel. Gebruik de gegevens in de afbeelding.
- (2p) Wat is juist over de stroomsterkte door de secundaire spoel? Die is gelijk aan / groter dan / kleiner dan de stroomsterkte door de primaire spoel. Leg je antwoord uit.
-
(1p) De spanning van de secundaire spoel is niet meteen geschikt voor het opladen van een accu. Daarom zit in de lader een elektronica-component die stroom in één richting doorlaat. Welke elektronica-component is dit?
-
(1p) De transformator in de lader blijkt niet ideaal te zijn. Wat is juist voor een niet-ideale transformator? Het secundaire vermogen is even groot als / groter dan / kleiner dan het primaire vermogen.
(Bron: Examen VMBO-T, 2022-1)
-
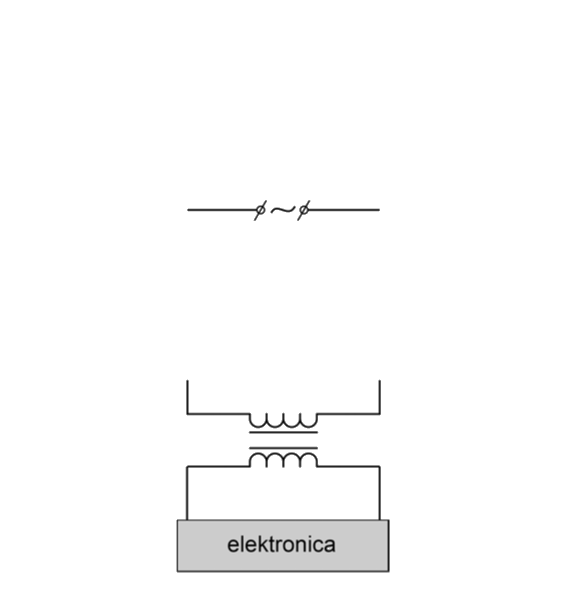
In de thuislader van een elektrische auto zit een transformator. Op het display van de thuislader kun je de spanning over en de stroomsterkte door de primaire spoel aflezen.
- (2p) Maak het onderstaande schakelschema compleet met spanningsmeter en stroommeter.
-
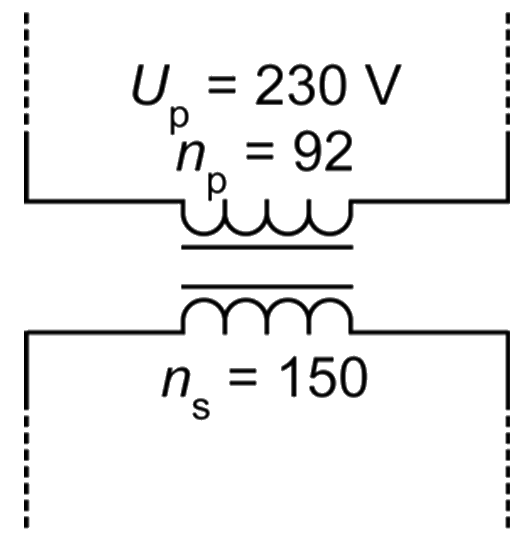
(3p) In de onderstaande afbeelding is een deel van het schakelschema van de transformator in de thuislader weergegeven. De secundaire stroomsterkte is 16 A. Bereken het secundaire vermogen. Bereken hiervoor eerst de secundaire spanning van de transformator.
-
(1p) De secundaire spoel in de thuislader levert wisselspanning. De thuislader levert gelijkspanning aan de accu van de auto. Welk elektronica-component zit hiervoor in de lader?
-
(2p) De transformator blijkt warm te worden. Welke conclusie over het rendement van de transformator is dan juist?
- Het rendement is gelijk aan 100%.
- Het rendement is groter dan 100%.
- Het rendement is kleiner dan 100%.
(Bron: Examen VMBO-T, 2022-2)
-
Een leerling maakt zelf een spoel door geïsoleerd koperdraad om de basis van de oplader van een elektrische tandenborstel te wikkelen. Deze spoel verbindt hij met twee leds.

- (1p) De koperdraad van een spoel is geïsoleerd om kortsluiting / overbelasting te voorkomen.
- (2p) De zelfgemaakte spoel heeft 18 windingen. Bereken het aantal windingen van de primaire spoel in de oplader. De secundaire spoel heeft een spanning van 1,2 V.
- (3p) De leerling leest op een energiemeter een (primair) vermogen van 0,8 W af. Laat met een berekening zien of hun transformator ideaal is. Ga uit van een stroomsterkte van 4,5 mA door de secundaire spoel.
(Bron: Examen VMBO-T, 2018-2)
-
Hieronder zijn vier schakelingen weergegeven met telkens 8 leds:
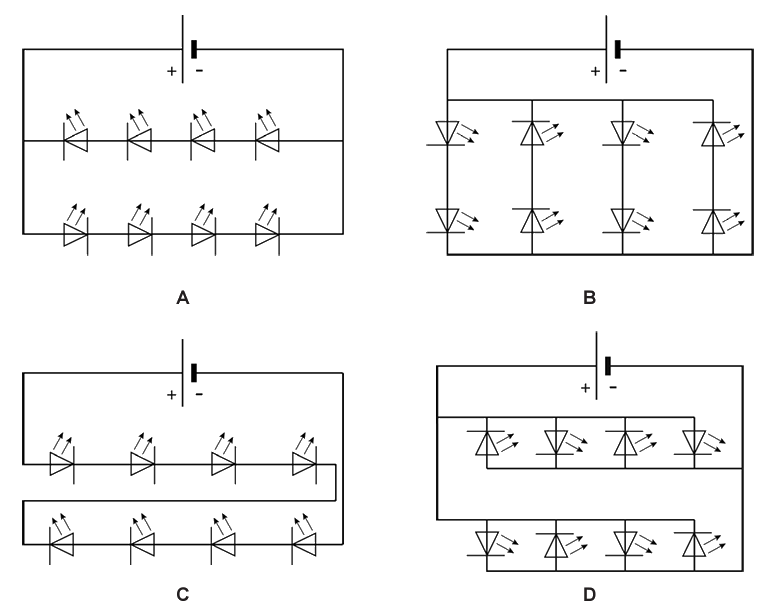
- (4p) Omcirkel de leds die branden.
- (2p) De leerling schakelt alle leds nu in de correcte richting. Over de spanningsbron staat een spanning van 12 V en de leds branden ideaal op een spanning van 1,5 V. Bereken welk van de schakelingen hiervoor correct geschakeld is.
(Bron: Examen VMBO-T, 2022-3)
-
(3p) Een leerling doet onderzoek naar een weerstandsdraad. De leerling vergeet regelmatig de schakelaar uit te zetten als hij even niet met de weerstand werkt. De weerstand verbruikt hierdoor onnodig elektriciteit en kan ook erg warm worden. Om dit te voorkomen soldeert de leerling een led parallel over de weerstandsdraad. Om ervoor te zorgen dat de led niet doorbrandt wordt ook een extra weerstand in serie met de led aangesloten. De led brandt als het circuit gesloten is. Teken de bijbehorende schakeling. Let op de richting van de led.
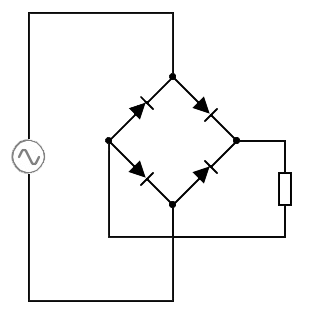
- (3p) In de onderstaande afbeelding is een zogenaamde gelijkrichter afgebeeld, bestaande uit vier diodes. Een gelijkrichter zet wisselspanning om in gelijkspanning. Deze schakeling wordt bijvoorbeeld gebruikt in de adapter van een laptop. Een laptop heeft namelijk gelijkspanning nodig, terwijl het stopcontact wisselspanning levert. De laptop is in de rechter schakeling weergegeven met het symbool van een weerstand. Leg met behulp van de afbeelding uit hoe wisselspanning wordt omgezet in gelijkspanning.
-
(2p) Een zaklampje bevat twee leds en een batterij van 3,6 V. Elke led werkt op een spanning van 3,6 V. Ontwerp dit schakelschema.
-
Tijdens een natuurkundeles bouwt een leerling een lichtgevoelige schakeling. Ze schakelt drie batterijen van elk 1,5 V in serie met een led en een LDR. Je ziet een afbeelding van haar opstelling.

- (3p) De leerling meet vervolgens de spanning over de led en de stroomsterkte door de led. Teken het schakelschema, inclusief drie batterijen, LDR, spanningsmeter, stroommeter en led.
- (4p) De leerling dekt de LDR af met haar vinger. Als de LDR wordt afgedekt neemt de weerstand van de LDR af / toe, neemt de spanning over de LDR af / toe en neemt de spanning over de led af / toe.
- (1p) De leerling haalt haar vinger van de LDR en sluit de led andersom aan. Welke stroomsterkte geeft de stroommeter dan aan?
(Bron: Examen VMBO-T, 2022-1)
|
| BINAS: |
|
| 7-12 |
Formules |
| 14 |
Symbolen elektrische schakelingen |
 (Afbeelding: ... / MdE; CC BY-SA 3.0)
(Afbeelding: ... / MdE; CC BY-SA 3.0)
 Demonstratievideo
Demonstratievideo
 Demonstratievideo
Demonstratievideo






 Leerdoelen:
Leerdoelen:
 Opdrachten
Opdrachten
 Voorbeeld
Voorbeeld
 Leerdoelen:
Leerdoelen:
 Opdrachten
Opdrachten





 Demonstratievideo
Demonstratievideo
 Demonstratievideo
Demonstratievideo


 Demonstratievideo
Demonstratievideo




 EXPERIMENT
EXPERIMENT

 Leerdoelen:
Leerdoelen:
 Opdrachten
Opdrachten




 EXPERIMENT
EXPERIMENT
 EXPERIMENT
EXPERIMENT



 EXPERIMENT
EXPERIMENT

 Demonstratievideo
Demonstratievideo


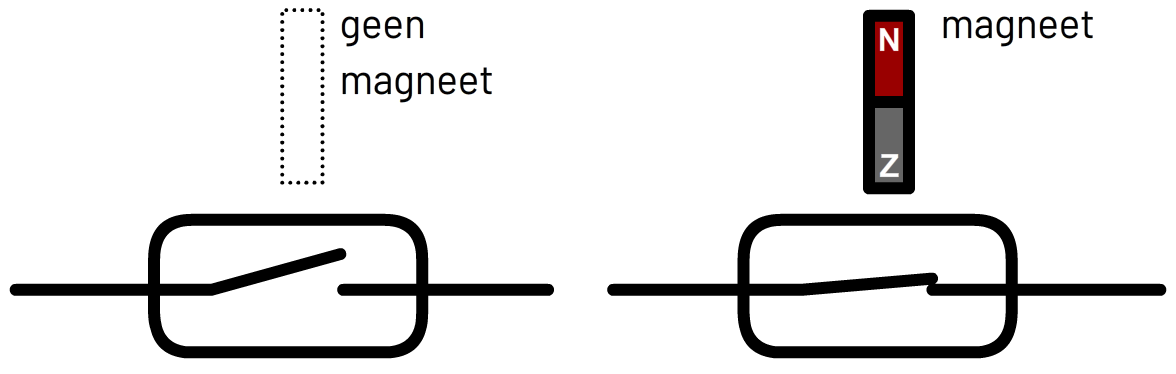




 Leerdoelen:
Leerdoelen:
 Opdrachten
Opdrachten


 Demonstratievideo
Demonstratievideo

 (Afbeelding: A. J. van der Wal; CC BY-SA 4.0)
(Afbeelding: A. J. van der Wal; CC BY-SA 4.0)
 (Afbeelding: Evan-Amos; PD)
(Afbeelding: Evan-Amos; PD)
 (Afbeelding: BillC; CC BY-SA 3.0)
(Afbeelding: BillC; CC BY-SA 3.0)

 Voorbeeld
Voorbeeld




 Leerdoelen:
Leerdoelen:
 Opdrachten
Opdrachten

























