Hoofdstuk 3
Kracht 2
§1 Versnelling §2 Traagheid §3 stabiliteit §4 Moment §5 Katrollen
§1 Versnelling
In dit hoofdstuk gaan we verder leren over kracht. We gaan het hebben over krachten werkende op draaiende voorwerpen en over het optillen van objecten met katrollen, maar we beginnen met de relatie tussen kracht en versnelling. Hiervoor is het eerst noodzakelijk dat we leren wat versnelling precies is.
De versnelling of vertraging (a) van een voorwerp kunnen we als volgt uitrekenen:
$$ a = \frac{\Delta v}{t} $$
|
Zoals je weet staat de v voor de snelheid. De Δ (spreek uit als "delta") staat voor "de toename van". Δv staat dus voor de toename van de snelheid tijdens een beweging. Als een voorwerp bijvoorbeeld versnelt van 10 m/s naar 14 m/s, dan is de toename van de snelheid gelijk aan Δv = 14 - 10 = 4 m/s. In formuletaal geldt:
| $$ \Delta v = v_{eind} - v_{begin} $$ |
De eenheid van de versnelling is m/s2. Dit betekent het volgende. Stel dat de snelheid van een voorwerp elke seconde 1 meter per seconde toeneemt. We zeggen dan dat de snelheid 1 meter per seconde per seconde toeneemt. De eenheid van de versnelling is dus m/s/s en dit korten we ook wel af tot m/s2.
Voorbeeld
|
|
Opdracht: Een persoon versnelt eenparig van 1,0 m/s naar 4,0 m/s in 6,0 seconden. Bereken de versnelling van deze persoon. Antwoord: Eerst schrijven we de gegevens op: vb = 1,0 m/s ve = 4,0 m/s t = 6,0 s Hiermee berekenen we eerst de toename van de snelheid (Δv): $$ \Delta v = v_{eind} - v_{begin} $$ $$ \Delta v = 4,0 - 1,0 = 3,0 \text{ m/s} $$Nu berekenen we de versnelling: $$ a = \frac{\Delta v}{t} $$ $$ a = \frac{3,0}{6,0} = 0,50 \text{ m/s}^2 $$ |
Let op het verschil tussen de toename van de snelheid (Δv) en de gemiddelde snelheid (vgem). Bij het beantwoorden van vragen is het belangrijk deze begrippen goed uit elkaar te houden. In het bovenstaande voorbeeld is de toename van de snelheid gelijk aan 4,0 - 1,0 = 3,0 m/s. In het hoofdstuk "Beweging" hebben we geleerd dat de gemiddelde snelheid bij een eenparige versnelling wordt gegeven door "vgem = (vb+ve)/2". In het bovenstaande voorbeeld is de gemiddelde snelheid dus (1,0 + 4,0)/2 = 2,5 m/s.
|
Voorbeeld
|
|
Opdracht: Een auto vertraagt van 40 m/s naar 25 m/s in 6,0 seconden. Bereken de vertraging van deze auto. Antwoord: Eerst schrijven we de gegevens op: vb = 40 m/s ve = 25 m/s t = 6,0 s Hiermee berekenen we eerst de toename van de snelheid (Δv): $$ \Delta v = v_{eind} - v_{begin} $$ $$ \Delta v = 25 - 40 = -15 \text{ m/s} $$Omdat we in dit geval te maken hebben met een afname van de snelheid vinden we voor Δv een negatief getal. Nu berekenen we de versnelling: $$ a = \frac{\Delta v}{t} $$ $$ a = \frac{-15}{6,0} = -2,5 \text{ m/s}^2 $$Zoals je kan zien is een negatieve versnelling een vertraging. Het wordt niet fout gerekend als je deze min vergeet. |
↓ VMBO VERSIES van deze VIDEOS komen binnenkort online!
↓ VMBO VERSIES van deze VIDEOS komen binnenkort online!
INSTRUCTIE:
Versnelling
|
Leerdoelen:
|
|
|
Opdrachten
|
|
§2 Traagheid
In deze paragraaf gaan we het verband leren tussen versnelling en kracht. We gaan aan de hand hiervan het begrip traagheid begrijpen.
In het hoofdstuk "Kracht I" hebben we geleerd dat de netto kracht op voorwerpen met een constante snelheid gelijk is aan nul newton. Als de netto kracht niet nul is, dan gaat het voorwerp versnellen of vertragen. In dat geval geldt:
$$ F_{netto} = ma $$
|
De bovenstaande formule wordt ook vaak in de volgende vorm geschreven:
$$ a = \frac{F_{netto}}{m} $$In deze vorm is goed te zien dat een voorwerp versnelt als er een netto kracht op werkt. Ook zien we dat deze versnelling kleiner wordt als de massa van het voorwerp groter is. Voorwerpen met een grote massa zijn dus moeilijk te versnellen en ook moeilijk af te remmen. Denk aan een gigantisch vrachtschip. Het kost heel veel kracht om zo'n schip in beweging te krijgen, maar als het eenmaal in beweging is, kost het ook heel veel kracht om het vrachtschip af te remmen. We noemen dit principe traagheid.
|
Demonstratievideo
| ||
|
|
Demonstratievideo
| ||
|
We merken traagheid ook als je in een auto zit die krachtig remt. De auto komt snel tot stilstand, maar de inzittenden schieten dan nog een stukje door naar voren (tot ze worden tegengehouden door hun gordels). Dit komt door de traagheid van de inzittenden. Ze willen doorbewegen met de snelheid die ze al hadden.
Nog een voorbeeld. Als een stilstaande auto van achter wordt geraakt, dan schiet de auto naar voren, maar de inzittenden willen door traagheid op hun plek stil blijven staan. Als gevolg heb je het gevoel dat je in je stoel wordt gedrukt (maar eigenlijk sta jij stil en drukt de stoel juist tegen jou aan). Om te voorkomen dat je hoofd bij deze botsing naar achter knakt hebben auto's een hoofdsteun. Op deze manier kan een whiplash voorkomen worden, waarbij de nekwervels beschadigen.
|
Voorbeeld
|
|
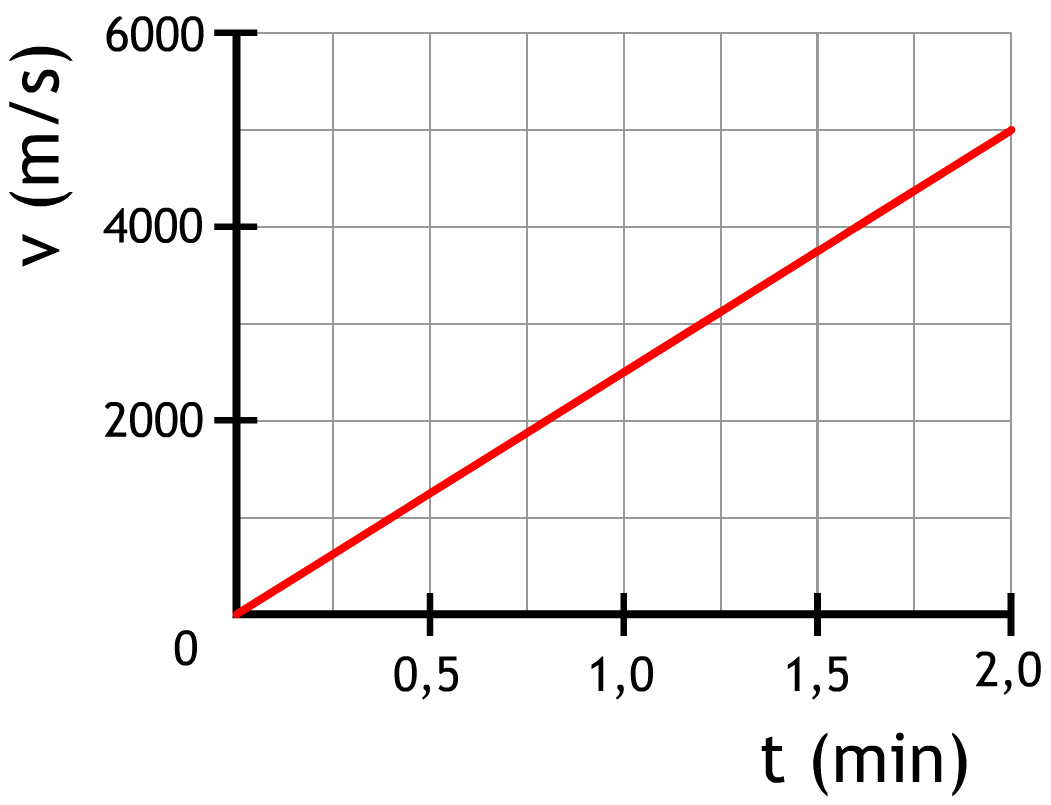
Vraag: In het onderstaande (v,t)-diagram is het opstijgen van een raket beschreven. De raket heeft een massa van 2,8 × 106 kg. Bepaal de versnelling die de raket onderging.
Antwoord: Voor de versnelling hebben we de begin- en de eindsnelheid nodig: vb = 0 m/s ve = 5000 m/s Hiermee berekenen we Δv: $$ \Delta v = v_e - v_b $$ $$ \Delta v = 5000 - 0 = 5000 \text{ m/s} $$We hebben ook de tijdsduur nodig. Volgens de grafiek duurde de versnelling 2,0 minuten. Omdat er 60 seconden in een minuut zitten, vinden we: t = 2,0 × 60 = 120 seconden Nu kunnen we de versnelling uitrekenen: $$ a = \frac{\Delta v}{t} $$ $$ a = \frac{5000}{120} = 41,667 \text{ m/s}^2 $$Vraag: Bereken de netto kracht werkende op de raket: Antwoord:
Hiervoor gebruiken we de formule "Fnetto = ma". De massa is gegeven in de vraag: m = 2,8 × 106 kg De netto kracht wordt hiermee: $$ F_{netto} = ma $$ $$ F_{netto} = 2,8 \times 10^6 \times 41,667 = 116666667 \text{ N} $$Vraag: Behalve de motorkracht werkt ook de zwaartekracht op de raket. Bereken zowel de zwaartekracht als de motorkracht. Antwoord:
Voor de zwaartekracht geldt: $$ F_z = mg $$ $$ F_z = 2,8 \times 10^{6} \times 10 = 2,8 \times 10^{7} \text{ N} $$In deze situatie werkt op de raket een motorkracht omhoog en een zwaartekracht omlaag. Er geldt dus: $$ F_{netto} = F_m - F_z $$Dit kunnen we omschrijven tot: $$ F_m = F_{netto} + F_z $$Als we dit invullen, dan vinden we: $$ F_{m} = 116666667 + 2,8 \times 10^7 = 144666667 \text{ N} $$
|
|
Voorbeeld
|
|
Vraag: Een persoon maakt een parachutesprong. In het eerste deel van de val is de parachute nog ingepakt. Ga na wat tijdens dit deel van de val gebeurt met de zwaartekracht, de luchtwrijvingskracht, de netto kracht en de versnelling. Antwoord: De zwaartekracht is volgens de formule gelijk aan "Fz = mg". De massa van de parachutespringer blijft gelijk, dus de zwaartekracht werkende op de persoon blijft ook gelijk. De luchtwrijvingskracht neemt toe doordat de snelheid van de parachutespringer toeneemt. De netto kracht is in dit geval gelijk aan de zwaartekracht (omlaag) min de luchtwrijvingskracht (omhoog). Doordat de luchtwrijving steeds groter wordt, wordt de netto kracht juist kleiner. De versnelling wordt volgens de formule "a = Fnetto / m" hierdoor ook kleiner. Vraag: Leg uit dat de snelheid van de parachutespringer uiteindelijk constant zal worden. Antwoord: In eerste instantie versnelt de parachutespringer. De luchtwrijvingskracht wordt hierdoor steeds groter. Uiteindelijk wordt de luchtwrijvingskracht even groot als de zwaartekracht. In dat geval is de netto kracht nul. In het vorige hoofdstuk hebben we geleerd dat de snelheid dan constant is.
|
↓ VMBO VERSIES van deze VIDEOS komen binnenkort online!
↓ VMBO VERSIES van deze VIDEOS komen binnenkort online!
INSTRUCTIE:
De tweede wet van Newton
|
Leerdoelen:
|
|
|
Opdrachten
|
|
§3 Stabiliteit
De komende twee paragrafen gaan over draaiende voorwerpen. Als een voorwerp omvalt, dan maakt het een draaibeweging. In deze eerste paragraaf bestuderen we wanneer voorwerpen omvallen en wanneer niet.
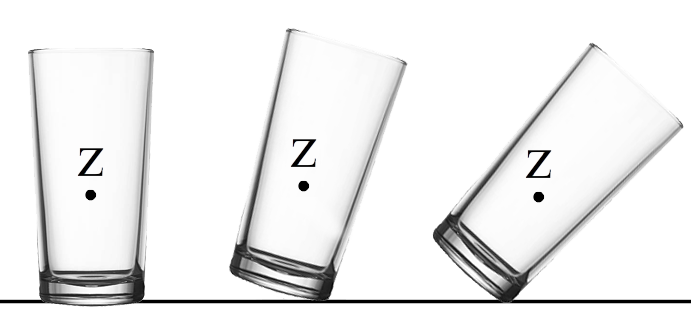
Om te begrijpen wanneer voorwerpen omvallen en wanneer niet, hebben we de begrippen zwaartepunt en draagvlak nodig. Het zwaartepunt van een voorwerp, ook wel het massamiddelpunt genoemd, is de plek waar het voorwerp in balans is. Neem bijvoorbeeld een homogene balk. Dit is een balk die overal dezelfde dichtheid heeft. In dat geval zit het zwaartepunt netjes in het midden (zie de onderstaande linker afbeelding). Het zwaartepunt kan je vinden door diagonalen te tekenen in de balk (zie de rechter afbeelding). Het zwaartepunt bevindt zich dan op de plek waar de lijnen kruisen. Op deze plek zetten we vaak een dikke punt met de letter Z (voor zwaartepunt) of de letter M (voor massamiddelpunt).
Bij een voorwerp met een ingewikkelde vorm, vind je het zwaartepunt door het voorwerp bijvoorbeeld op je vinger te balanceren. Het zwaartepunt bevindt zich dan op de lijn boven je vinger (zie de onderstaande afbeelding).
(Afbeelding: APN MJM; CC BY-SA 3.0-mod)
Het zwaartepunt is ook de plek waar de zwaartekracht aangrijpt. De vectorpijl van de zwaartekracht starten we dus altijd in het zwaartepunt.
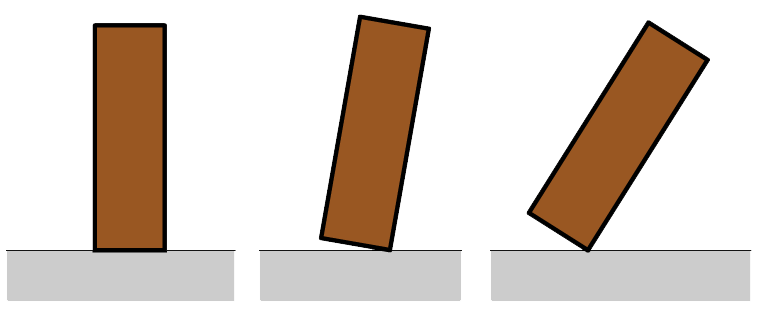
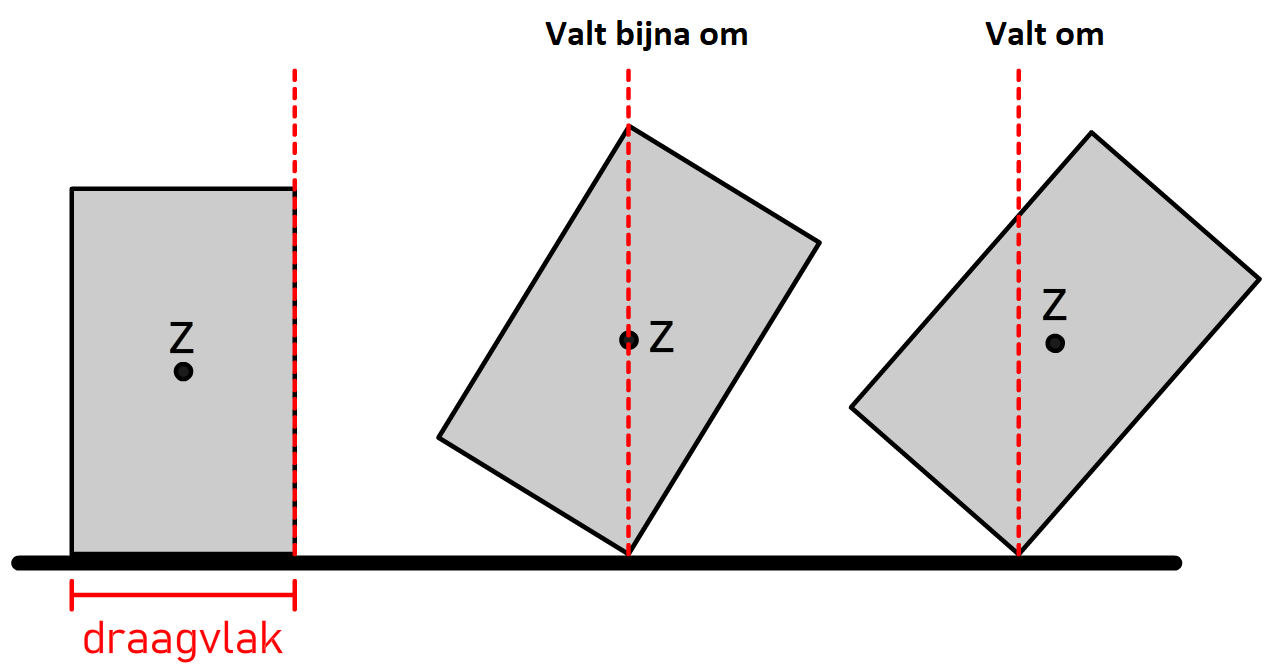
Het oppervlak tussen de verst liggende punten waarop een voorwerp staat noemen we het draagvlak. In het onderstaande linker voorwerp is het draagvlak simpelweg gelijk aan de onderzijde van het blok. Bij de stoel in de rechter afbeelding is het draagvlak niet alleen het oppervlak onder de stoelpoten, maar ook het oppervlak ertussen. Een voorwerp valt om als het zwaartepunt van het voorwerp zich niet meer boven het draagvlak bevindt. Dit is duidelijk te zien in de drie linker onderstaande afbeeldingen.
(Afbeelding: ... / MET; CC0)
|
Leerdoelen:
|
|
|
Opdrachten
|
|
§4 Moment
In deze paragraaf gaan we rekenen met krachten werkende op draaiende voorwerpen. We gebruiken hiervoor het begrip moment. Ook gaan we momentevenwichten bestuderen.
In deze paragraaf gaan we het hebben over het principe van de hefboom. Met een hefboom kan je een kleine kracht omzetten in een grote kracht. In de onderstaande afbeelding wordt dit principe gebruikt bij het openen van verfpotten. Zoals je wellicht uit ervaring weet, gaat het openen van een verfpot veel gemakkelijker met een langere schroevendraaier. In de rechter afbeelding geldt hetzelfde principe. Een moer omdraaien met alleen je hand is lastig, maar als je de lengte van een sleutel gebruikt, dan kost dit weinig kracht.
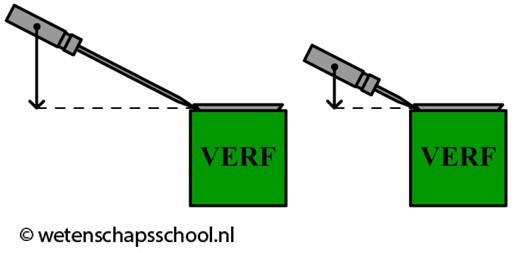
Een hefboom heeft altijd een draaipunt. Dit is duidelijk te zien bij een wip. In de afbeelding linksonder zien we twee personen met gelijke massa die op gelijke afstanden van het draaipunt zitten. De wip is nu in evenwicht. In de rechter afbeelding gaat de linker persoon iets verder van het draaipunt zitten en als gevolg zal de wip aan deze kant dalen. Er geldt dus: hoe verder de persoon van het draaipunt gaat zitten, hoe meer invloed de persoon heeft op de draaiing van de wip. We zeggen in zo'n geval dat de persoon dan een groter moment uitoefent op de wip.
We kunnen het moment als volgt berekenen:
$$ M = F \times l $$
|
De arm (l) is de afstand van het draaipunt tot de kracht die op het voorwerp werkt.
|
Demonstratievideo
| ||
|
Als een voorwerp in evenwicht is, dan is de som van de momenten die het voorwerp linksom pogen te draaien gelijk aan de som van de momenten die het voorwerp rechtsom pogen te draaien. In formuletaal wordt dit:
$$ M_{L} = M_{R} \;\;\;\; \text{(evenwicht)}$$
|
|
Demonstratievideo
| ||
|
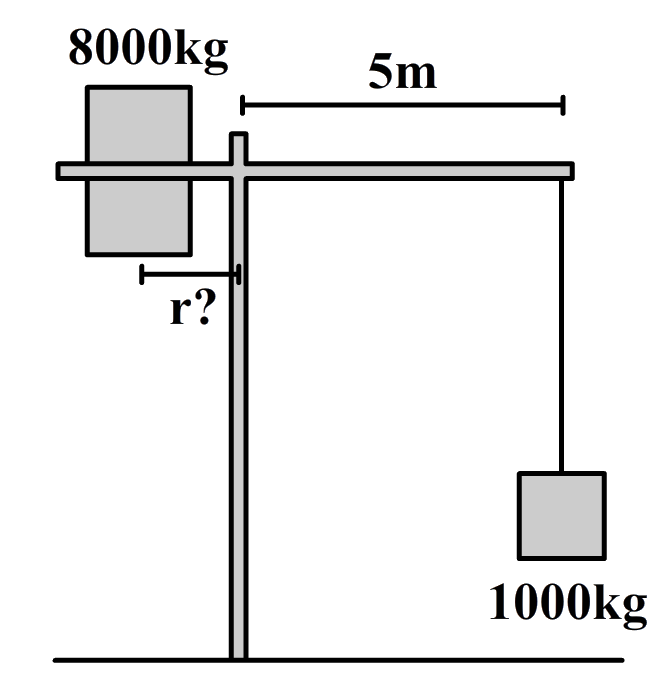
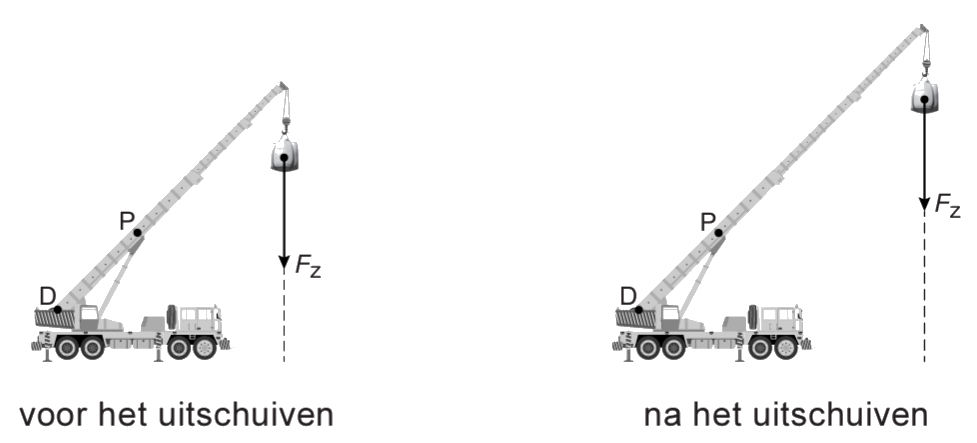
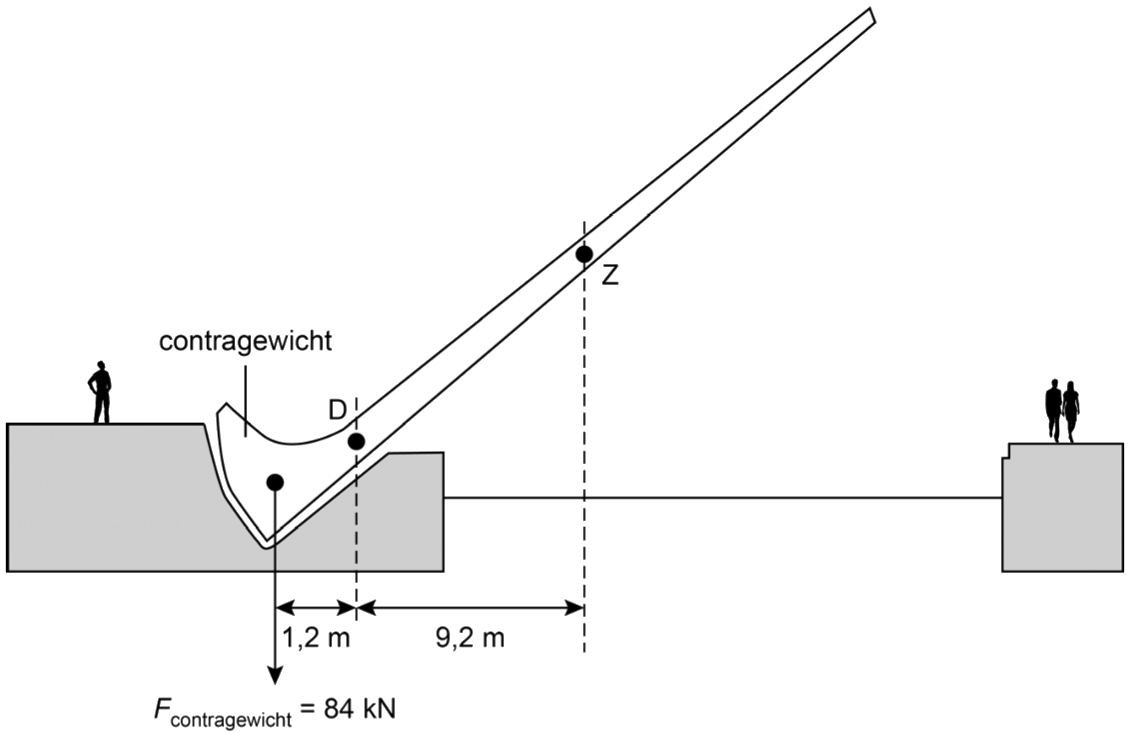
Een bekend voorbeeld waar het momentenevenwicht een belangrijke rol speelt is de hijskraan. Deze gigantische kranen kunnen zware voorwerpen optillen zonder om te vallen. Dit kan omdat de kraan in evenwicht wordt gehouden door een contragewicht (zie de onderstaande afbeelding). Door de positie van dit contragewicht te verplaatsen, en dus de arm te veranderen, kan de kraan telkens in evenwicht worden gehouden.
|
Voorbeeld
|
|
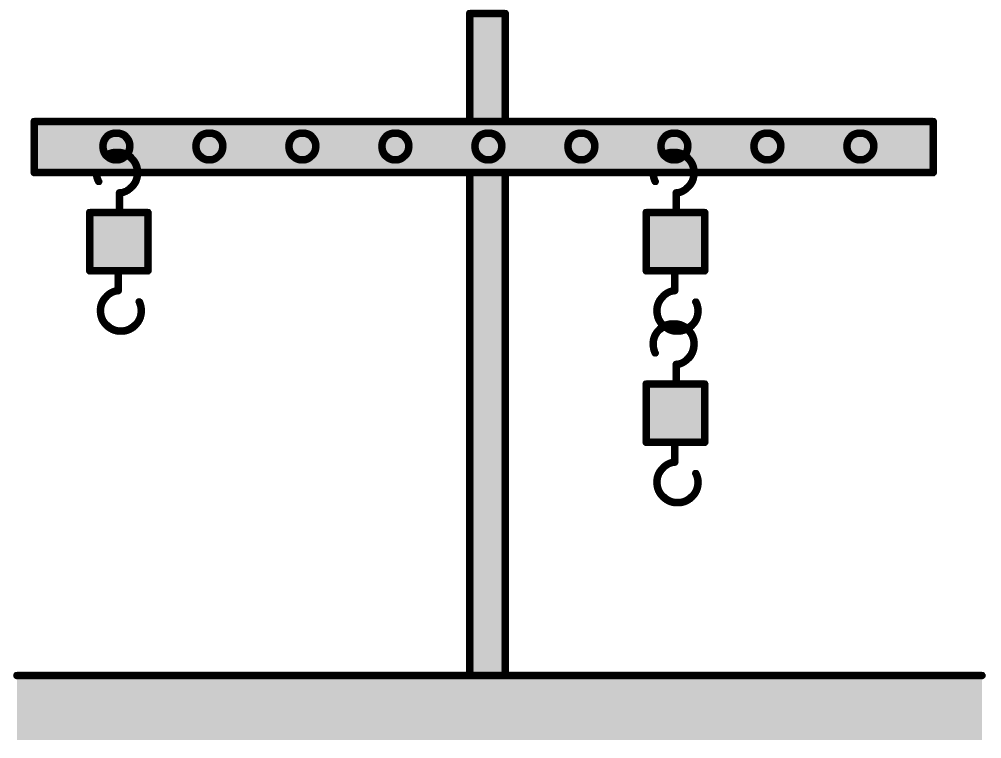
Vraag: In de onderstaande afbeelding zijn drie blokjes van 50 gram opgehangen aan een balans. Laat zien dat de blokjes in evenwicht hangen. De afstand tussen de gaatjes waaraan de blokjes hangen is 2,5 cm.
Antwoord: De blokjes hangen in evenwicht als het moment dat de balans linksom probeert te draaien gelijk is aan het moment dat de balans rechtsom probeert te draaien. Voor de linker en de rechter blokjes geldt: mlinks = 50 g = 0,050 kg mrechts = 50 × 2 = 100 g = 0,100 kg Hiermee kunnen we de zwaartekracht uitrekenen: $$ F_z = mg $$ $$ F_{z,links} = 0,050 \times 10 = 0,50 \text{ N} $$ $$ F_{z,rechts} = 0,100 \times 10 = 1,00 \text{ N} $$De arm is de afstand van het draaipunt tot de plek waar de blokjes aan de balans trekken. In de onderstaande afbeelding zijn beide armen getekend.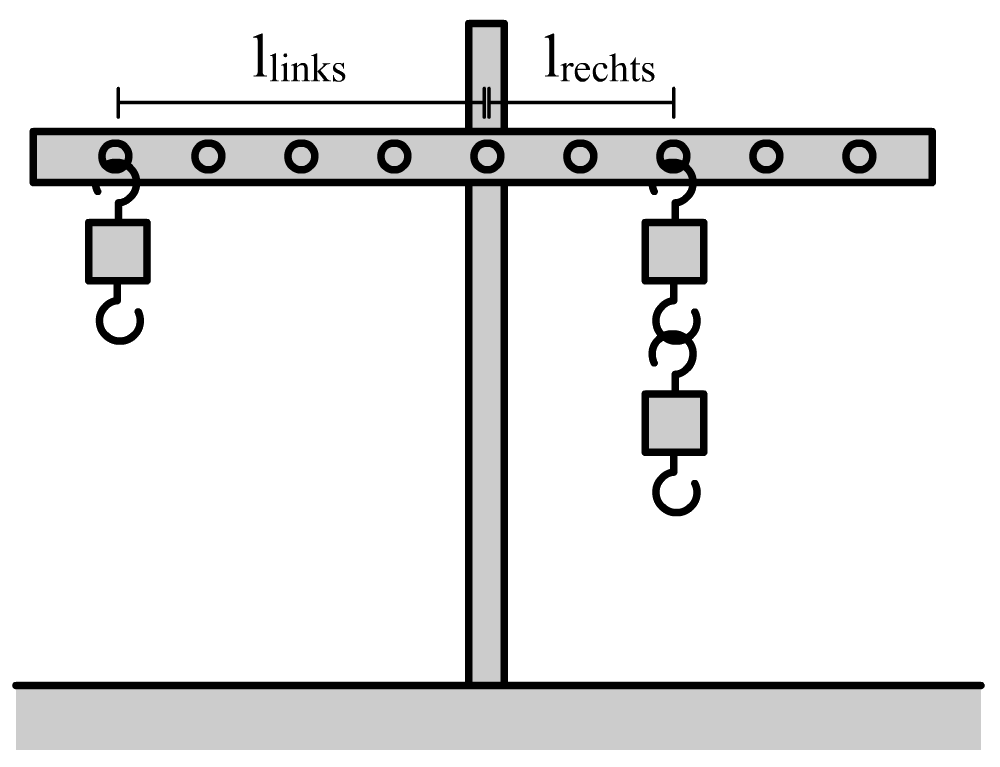 
De afstand tussen twee gaatjes is 2,5 cm. We vinden dus: llinks = 4 × 2,5 = 10,0 cm lrechts = 2 × 2,5 = 5,0 cm Nu kunnen we het moment in beide gevallen uitrekenen: $$ M = F \times l $$ $$ M_{links} = 0,50 \times 10,0 = 5,0 \text{ Nm} $$ $$ M_{rechts} = 1,00 \times 5,0 = 5,0 \text{ Nm} $$De momenten zijn gelijk, dus de blokjes hangen inderdaad in evenwicht.
|
|
Voorbeeld
|
|
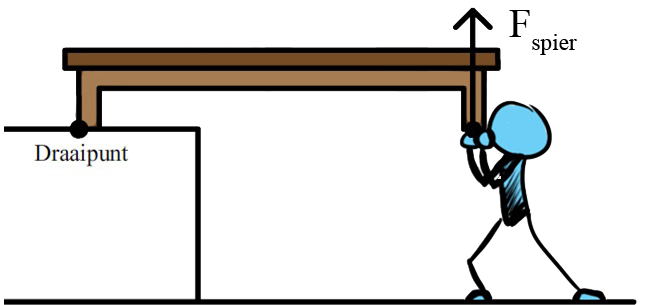
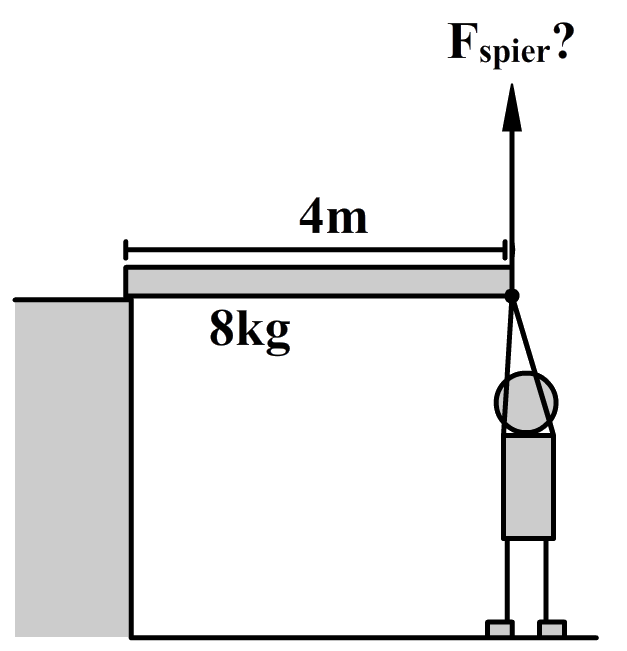
Vraag: In de volgende afbeelding tilt een persoon een bank op die op een verhoging ligt. De bank is van poot tot poot 4,0 m lang en heeft een massa van 10 kg. Bereken de spierkracht die de persoon moet uitoefenen om de bank in horizontale positie te houden.
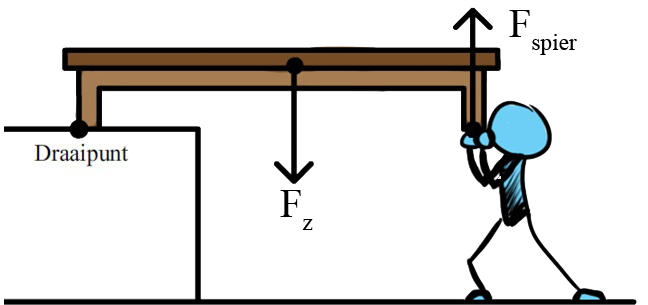
Antwoord: Het zwaartepunt van de bank bevindt zich in het midden van de bank. Het zwaartepunt is ook de plek waar de zwaartekracht aangrijpt. Op deze plek tekenen we dan ook de zwaartekracht (zie de onderstaande afbeelding)./p> De arm van de zwaartekracht is de afstand van het draaipunt tot de zwaartekracht. Omdat de zwaartekracht in het midden van de bank werkt, is de bijbehorende arm dus 4,0 / 2 = 2,0 m lang. De afstand van het draaipunt tot de spierkracht is 4,0 meter. De arm van de spierkracht is dus 4,0 m.
Dan maken we gebruik van het momentenevenwicht: $$ M_{links} = M_{rechts} $$De kracht die de bank linksom draait is de spierkracht en de kracht die de bank rechtsom probeert te draaien is de zwaartekracht. $$ M_{spier} = M_z $$ $$ F_{spier} \times l_{spier} = F_z \times l_z $$We vullen nu de gegevens zo veel mogelijk in. Aan de rechterzijde gebruiken we hier Fz = mg = 10 × 10 = 100 N: $$ F_{spier} \times 4 = 100 \times 2 $$Als we de rechterzijde uitrekenen, dan vinden we: $$ F_{spier} \times 4 = 200 $$Hiermee kunnen we de spierkracht uitrekenen: $$ F_{spier} = \frac{200}{4} = 50 \text{ N} $$
|
|
Voorbeeld
|
|
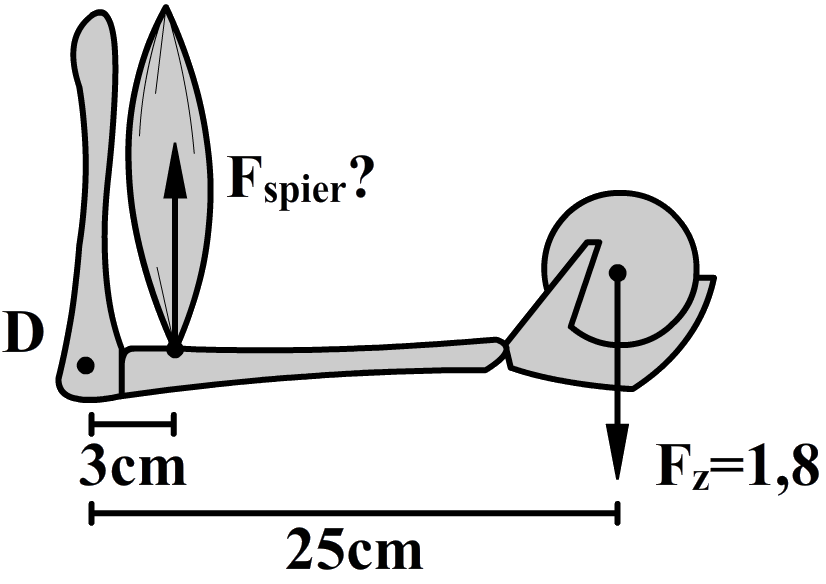
Vraag: Om een moer los te draaien is een is een bepaald moment nodig. Een persoon kan dit moment leveren door een kracht uit te oefenen op punt A en punt B van de rechter sleutel. Leg uit in welk geval de persoon een grotere kracht moet uitleggen.
Antwoord: De arm op punt B is langer. Volgens de formule "M = Fl" is bij een gelijk moment en een grotere arm de kracht die nodig is kleiner.
|
↓ VMBO VERSIES van deze VIDEOS komen binnenkort online!
↓ VMBO VERSIES van deze VIDEOS komen binnenkort online!
INSTRUCTIE:
Momentenevenwicht
|
Leerdoelen:
|
|
|
Opdrachten
|
|
§5 Katrollen
In deze laatste paragraaf bestuderen we de werking van katrollen.
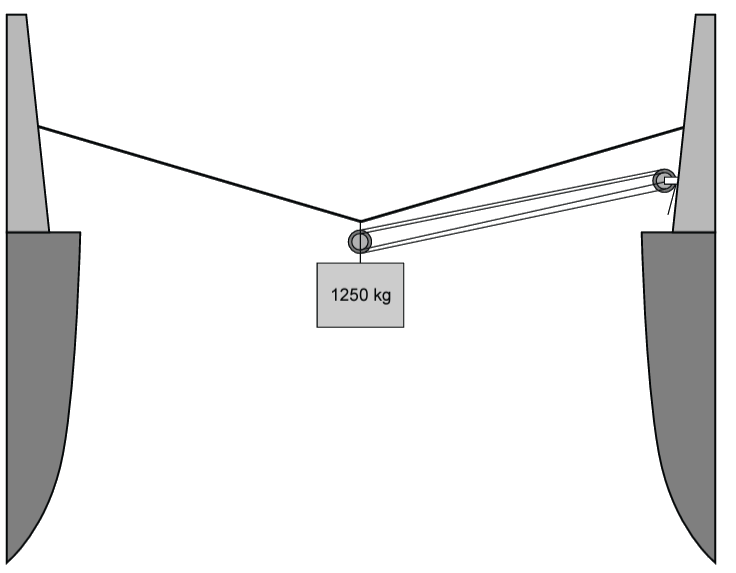
Een katrol kan worden gebruikt om een zwaar voorwerp makkelijker te kunnen optillen. Er zijn twee soorten katrollen, vaste en losse katrollen. Een vast katrol zit vast op een hoog punt en doet niets anders dan het omdraaien van de kracht. Dit zien we in de onderstaande linker afbeelding. We kunnen hiermee een voorwerp omhoog tillen door een touw naar beneden te trekken. Voordeel is dat je nu aan de kabel kan hangen en de zwaartekracht het werk kan laten doen.
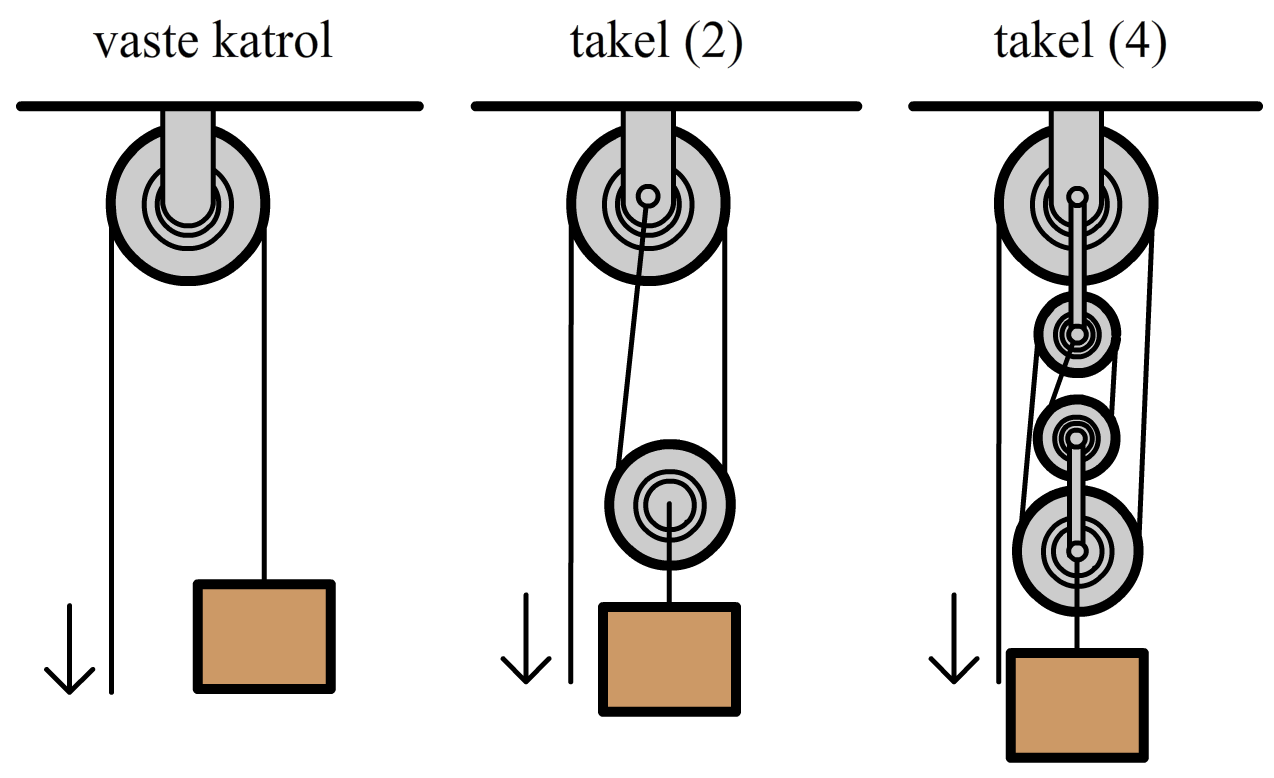
In de middelste afbeelding is ook een los katrol toegevoegd. Deze katrol zit vast aan het voorwerp dat je wilt optillen. Bij toevoeging van een los katrol spreken we van een takel. Het voordeel van een takel is dat het nu minder kracht kost om een voorwerp op te tillen. In het middelste voorbeeld zien we dat een voorwerp met een losse katrol aan twee touwen hangt. Als gevolg kost het maar de helft van de kracht om het voorwerp op te tillen. Een nadeel is wel dat je twee keer zoveel touw naar beneden moet trekken. In het rechter voorbeeld wordt het blok omhoog gehouden door twee losse katrollen met vier touwen (tel ze zelf na). De kracht nodig om het blok op te tillen is hierdoor vier keer zo klein, maar je moet wel vier keer zoveel touw naar beneden trekken.
Over het algemeen geldt dat het aantal losse katrollen keer twee of het aantal touwen aan de losse katrollen ons vertelt met welke factor de kracht afneemt en de lengte van het touw toeneemt.
|
Voorbeeld
|
|
Vraag: Een bank van 200 kg wordt opgetild met behulp van een takel bestaande uit 3 lossen en 3 vaste katrollen. Bereken met welke kracht je aan het touw moet trekken. Antwoord: De zwaartekracht werkende op de bank is: Fz = mg Fz = 200 × 10 = 2000 N Met 3 losse katrollen wordt de kracht 3 × 2 = 6× zo klein. Er geldt dus: 2000 / 6 = 333,3 N Vraag: De bank moet 7 meter omhooggetild worden. Bereken hoeveel meter touw je hiervoor nodig hebt. Antwoord: Als de kracht 6× zo klein wordt, dan wordt het benodigde touw 6× zo lang: 7 × 6 = 42 m Je hebt dus 42 meter touw nodig.
|
|
Leerdoelen:
|
|
|
Opdrachten
|
|
| BINAS: | |
| 7-12 | Formules |