Hoofdstuk 2
Mengsels

§1 Zuivere stoffen en mengsels
§2 Mengsels
§3 Concentratie
§4 Significante cijfers
§5 Volume- en massaprocent

§1 Zuivere stoffen en mengsels

In dit hoofdstuk gaan we mengsels bestuderen. Het is hiervoor nodig eerst het verschil tussen zuivere stoffen en mengsels te bespreken.

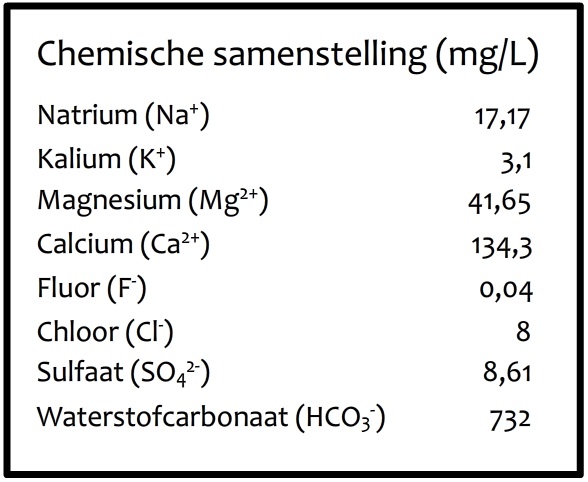
Als een bepaald materiaal uit één soort stof bestaat, dan noemen we dit materiaal zuiver. Helemaal zuiver zijn stoffen eigenlijk nooit, maar er zijn een aantal stoffen die redelijk in de buurt komen. Denk bijvoorbeeld aan een suikerklontje of een stuk koperdraad. Als een materiaal uit meerdere stoffen bestaat, dan noemen we dit een mengsel. Een voorbeeld van een mengsel is beton. Dit is een mengsel van water, zand, cement en grind. Zelfs het water uit de kraan is een mengsel. Hieronder zien we een label van een flesje mineraalwater. Op dit label staat dat er in het water allerlei stoffen zijn opgelost, zoals calcium, magnesium en natrium. Dat deze stoffen in water zijn opgelost is trouwens geen enkel probleem. Sterker nog, deze mineralen zijn belangrijk voor verschillende lichaamsfuncties.

Het is trouwens wel mogelijk om deze stoffen uit water te verwijderen (in een later hoofdstuk bespreken we hoe we dit kunnen doen). In dat geval verkrijgen we wel zuiver water. We noemen dit ook wel gedestilleerd water. Gedestilleerd water wordt geregeld in scheikunde-experimenten gebruikt.

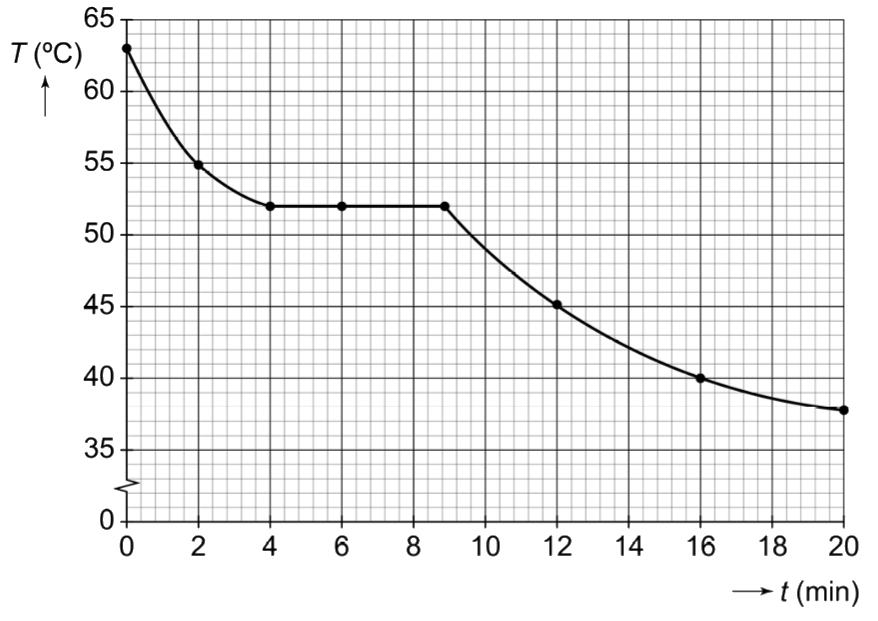
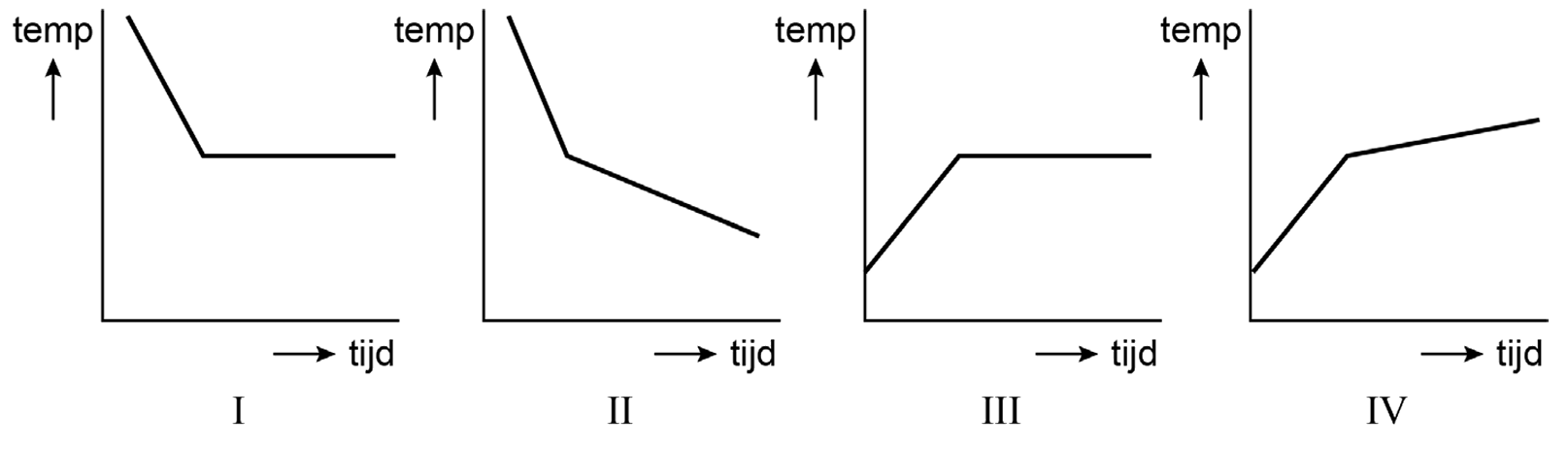
We kunnen met een simpel experiment bepalen of een materiaal een zuivere stof of een mengsel is. Neem bijvoorbeeld de zuivere stof tin. Als we deze stof geleidelijk verwarmen, dan begint het te smelten bij een temperatuur van 232 °C. Gedurende de periode waarin het tin aan het smelten is, blijft de temperatuur 232 °C. We noemen dit het smeltpunt van tin (zie de onderstaande afbeelding). Alle warmte die nu wordt toegevoegd, wordt niet gebruikt om het tin op te warmen, maar om het tin te laten smelten.

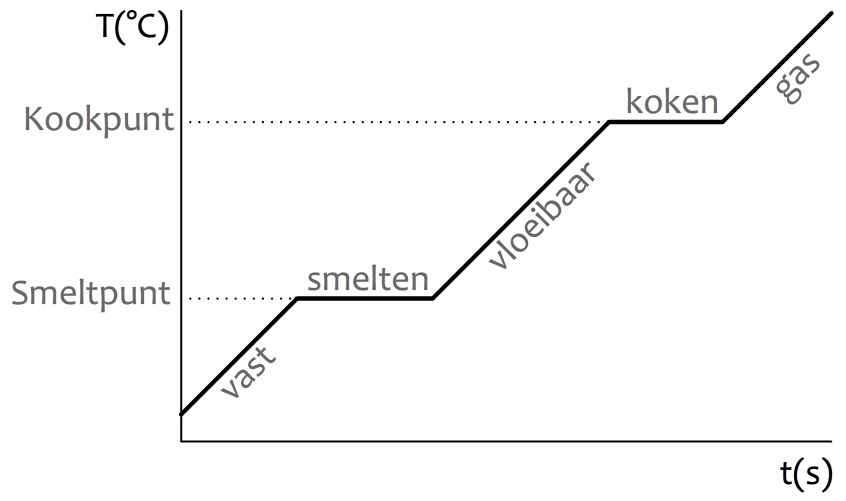
Als je de temperatuur van tin verhoogd tot 2602 °C, dan begint het te koken. Ook hier zien we dat de temperatuur constant blijft tot het moment dat al het tin is verdampt.

Als we een mengsel verwarmen, dan zien we een ander patroon. Omdat de verschillende stoffen in een mengsel allemaal andere smeltpunten hebben, is er geen eenduidig smeltpunt. Als gevolg blijft de temperatuur tijdens het smelten en het koken niet constant. De temperatuurstijging tijdens het smelten noemen we het smelttraject en de temperatuurstijging tijdens het koken het kooktraject (zie de onderstaande afbeelding).

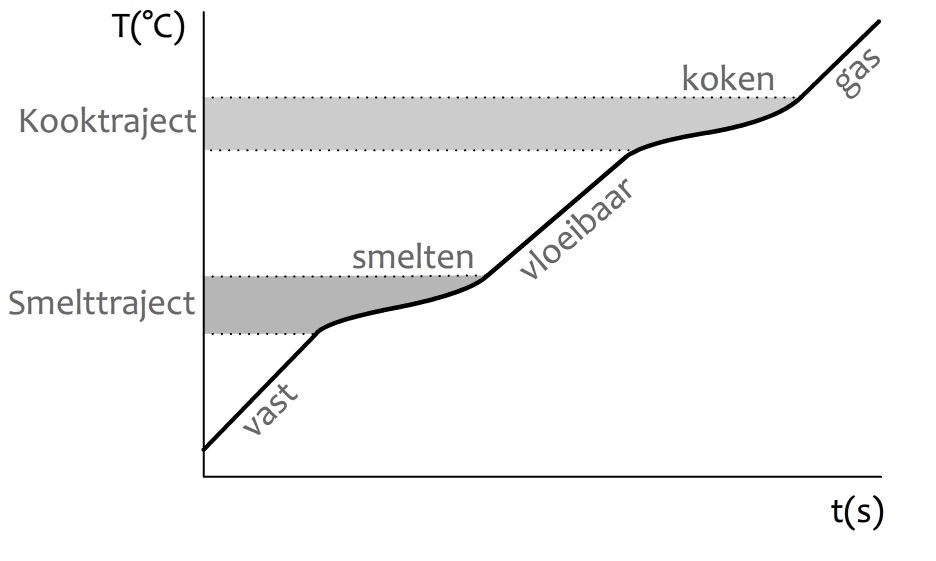
Door te achterhalen of een stof een smeltpunt of een smelttraject heeft, kunnen we dus bepalen of een stof een zuivere stof of een mengsel is!

Leerdoelen:

Zorg dat je weet dat kraanwater geen zuivere stof is, maar gedestilleerd water wel.

Zorg dat je kan aantonen of een stof een zuivere stof of een mengsel is met behulp van het smelt- of kookpunt of het smelt- of kooktraject.

Opdrachten

(1p) Is kraanwater een zuivere stof of een mengsel?

(1p) Beschrijf een experiment waarmee je kan bepalen of een stof zuiver is of een mengsel.

3. Een leerling stopt een beetje kaarsvet in een reageerbuis. Ze verwarmt het kaarsvet en laat het daarna afkoelen. Om de twee minuten meet de leerling de temperatuur en het resultaat staat in het onderstaande diagram.

(2p) Leg aan de hand van het diagram uit of kaarsvet een zuivere stof is.

(3p) Welke fase(n) heeft dit kaarsvet op t = 2 min, t = 6 min en t = 12 min?
(Bron: Examen VMBO-T, 2022-2)

Een leerling wil weten of margarine een zuivere stof is of een mengsel. Ze smelt margarine en laat het daarna afkoelen in een koelkast. Tijdens het afkoelen meet ze elke minuut de temperatuur. Ze schrijft haar metingen op in een tabel:

t(min.) T(°C)

0 60

1 51

2 42

3 33

4 30

5 27

6 25

7 15

8 5

(4p) Bepaal het smeltpunt of het smelttraject van margarine. Maak hiervoor eerst een grafiek van de bovenstaande tabel.

(1p) Leg aan de hand van de metingen uit of margarine een mengsel of een zuivere stof is.

In een gesteente komen onder meer de stoffen aluminiumoxide en ijzeroxide voor. Heeft dit type gesteente een smelttraject of smeltpunt.

(3p) Brons is een legering bestaande uit koper en tin. Welk van de onderstaande diagrammen geeft het temperatuurverloop bij het stollen van brons weer?

(Bron: Examen VMBO-T)

§2 Mengsels

In deze paragraaf gaan we het hebben over twee soorten mengsels: oplossingen en suspensies.

Een stof waar we doorheen kunnen kijken noemen we helder. Als we een stof met een vloeistof mengen en het mengsel blijft helder, dan spreken we van een oplossing. Een voorbeeld van een oplossing is zeewater. In zeewater zit zout opgelost, maar toch kunnen we het zout niet zien. Een ander voorbeeld is het oplossen van suiker in thee. Ook hier lijkt het suiker te "verdwijnen" in het water. Oplossingen kunnen wel een kleur hebben. Thee heeft bijvoorbeeld vaak een oranje of bruine kleur.

Hoe komt het dat oplossingen helder zijn? Neem bijvoorbeeld zeewater. Zeewater is helder omdat de zoutdeeltjes zich volledig verspreiden in het water (zie de onderstaande afbeelding). We noemen een dergelijk mengsel een homogeen mengsel. Een zoutdeeltje is een miljoen keer kleiner dan een millimeter en kan dus niet met onze ogen gezien worden. Omdat alle deeltjes los van elkaar door het water bewegen, kunnen we ze dus niet zien.

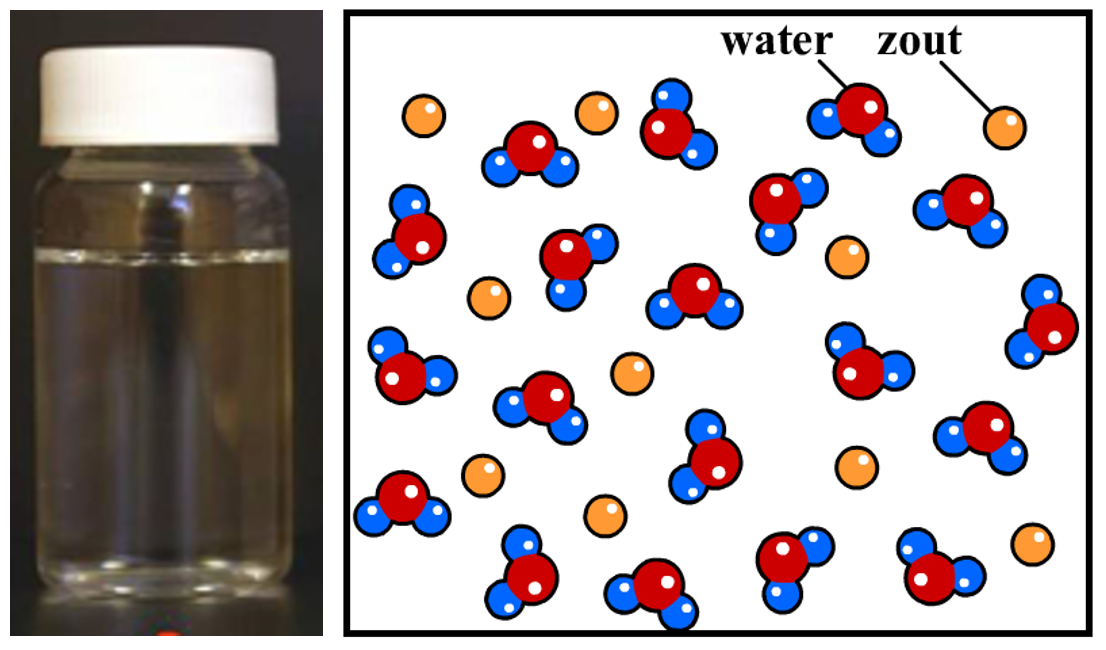
Ook gassen vormen homogene mengsels. Neem bijvoorbeeld de lucht. De lucht bestaat o.a. uit de gassen stikstof, zuurstof en een beetje koolstofdioxide. Omdat de deeltjes in een gas los van elkaar bewegen, kunnen gassen altijd goed mengen en vormen ze dus altijd homogene mengsels. Elk mengsel van gassen is daarom altijd helder (maar net als bij vloeistoffen kunnen deze gassen wel een kleur hebben).

Een vloeistof waar we niet doorheen kunnen kijken noemen we troebel. Als we een stof met een vloeistof mengen en het mengsel wordt troebel, dan spreken we van een suspensie. Er ontstaat bijvoorbeeld een suspensie als we krijtstof mengen met water. Een suspensie ontstaat doordat het krijt zich niet perfect mengt met het water. De krijtdeeltjes blijven in kleine klontjes aan elkaar plakken en deze klontjes zweven rond in het water (zie de onderstaande afbeelding). Omdat deze klontjes groot genoeg zijn om met onze ogen te kunnen zien, kunnen we niet door een suspensie heen kijken. We noemen een dergelijk mengsel een heterogeen mengsel.

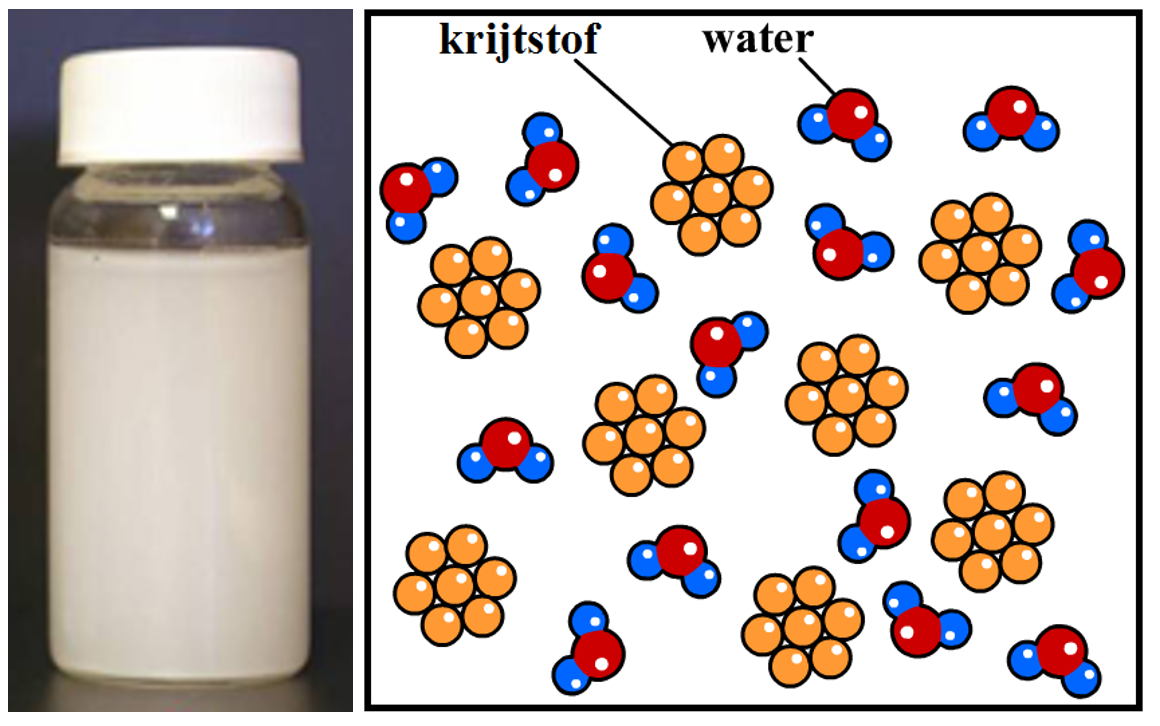
Naast suspensies bestaan er ook nog andere heterogene mengsels. Een voorbeeld is rook. Rook is een collectie van kleine stukjes vaste stof die in de lucht zweven. Rook is dus geen gas, maar bestaat uit kleine stukjes vaste stof (zie de twee onderstaande afbeeldingen).

(Afbeelding: US Coast Guard; PD / Reinald Kirchner CC BY-SA 2.0)

Een ander voorbeeld is een nevel. Nevel is een collectie van kleine vloeibare druppeltjes die in de lucht zweven. We kunnen bijvoorbeeld een nevel maken door een fles haarlak of deodorant te spuiten. Ook wolken en mist zijn nevels. Een nevel is dus geen gas, maar bestaat uit kleine waterdruppeltjes.

(Afbeelding: Pixabay; PD / Keith Miller; PD / Pixabay; PD)

Een ander voorbeeld van een heterogeen mengsel is schuim. Een schuim bestaat uit gasbelletjes die zich in een vloeistof of een vaste stof bevinden. Denk bijvoorbeeld aan de "prik" in cola. Dit bestaat uit kleine belletjes koolstofdioxide. Een ander voorbeeld is piepschuim. Dit bestaat uit plastic bolletjes gevuld met lucht.

(Afbeelding: Pixabay; PD)

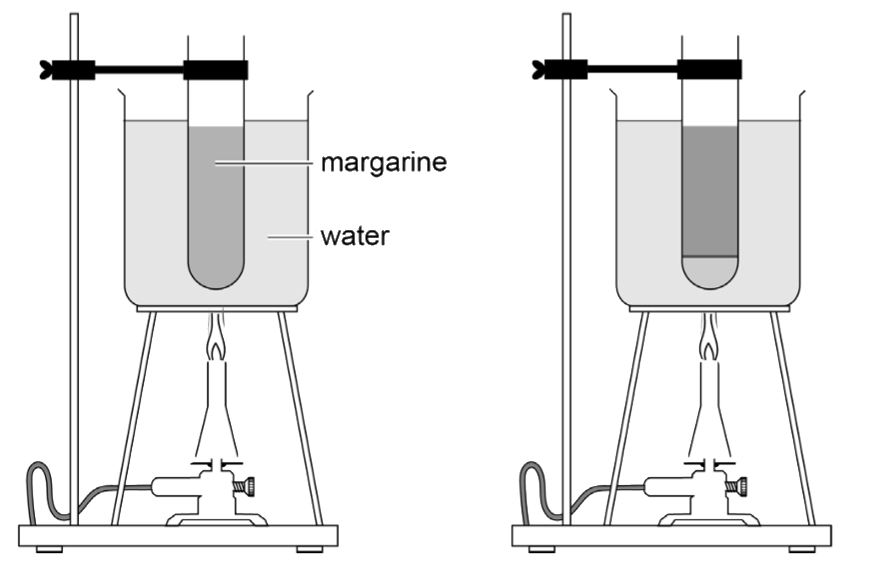
Het laatste voorbeeld van een heterogeen mengsel is een emulsie. Een emulsie bestaat uit stoffen die onder normale omstandigheden niet mengen, maar die door een extra stof, genaamd de emulgator, toch mengen. Een aantal emulgatoren kan je in BINAS vinden tussen de E-nummers.

Voorbeelden van emulsies zijn mayonaise en crèmes. Mayonaise bestaat voornamelijk uit olie en een beetje azijn. Zoals je in de linker onderstaande afbeelding kan zien, mengen deze vloeistoffen normale omstandigheden niet. Als emulgator voegen we eigeel toe en zo ontstaat de emulsie mayonaise.

(Afbeelding: Victor Blacus; CC BY-SA 4.0 / Takeaway; CC BY-SA 3.0)

Een crème is een emulsie bestaande uit o.a. water, een vet of een olie en een emulgator. Crèmes worden op de huid gesmeerd om de huid te verzorgen of als medicatie tegen bijvoorbeeld huidaandoeningen.

(Afbeelding: Victor Blacus; CC BY-SA 4.0 / Takeaway; CC BY-SA 3.0)

Crèmes behoren trouwens tot de cosmetische middelen. Dit zijn producten waarmee je je lichaam schoonmaakt, verzorgt of verfraaid. Hiertoe behoren dus crèmes, maar bijvoorbeeld ook zeep, haargel, deodorant en make-up.

Hieronder zijn de homogene en heterogene mengsels uit de tekst nog eens samengevat:

Homogeen mengsel	Heterogeen mengsel
Oplossing	Suspensie
Gasmengsel	Rook
	Nevel
	Schuim
	Emulsie

Leerdoelen:

Zorg dat je weet dat heldere mengsels oplossingen zijn en troebele mengsels suspensies. Zorg ook dat je beide mengsels op atomair niveau kan beschrijven.

Zorg dat je weet dat gasmengsels altijd transparant zijn, maar wel een kleur kunnen hebben.

Zorg dat je de verschillende soorten heterogene mengsels, zoals suspensies, rook, nevel, schuim, en emulsies kan herkennen en beschrijven.

Zorg dat je weet wat een emulgator doet en zorg dat je weet dat mayonaise en crémes voorbeelden zijn van emulsies.

Opdrachten

(1p) Een homogeen mengsel is helder / troebel. Dit komt doordat de deeltjes in het mengsel zich geheel verspreiden / in klontjes aan elkaar zitten.

(1p) Een heterogeen mengsel is helder / troebel. Dit komt doordat de deeltjes in het mengsel zich geheel verspreiden / in klontjes aan elkaar zitten.

(4p) Maak schetsen van de volgende fenomenen, waarbij je deeltjes voorstelt als kleine bolletjes:

Een homogeen mengsel

Een heterogeen mengsel

Twee vloeistoffen die niet mengen met een verschillende dichtheid

Een mengsel van zuurstof en stikstof (twee gassen)

(4p) Welke van de volgende mengsels zijn homogeen en welke heterogeen?

Leidingwater

Melk

Limonade

Lucht

Pindakaas

Thee

Boter

(1p) Noem twee emulsies.

(1p) Mayonaise bestaat voornamelijk uit olie en een beetje azijn. Ook wordt als emulgator een klein beetje eigeel gebruikt. Wat gebeurt er als je de emulgator niet toevoegd?

(2p) Beschrijf het verschil tussen nevel en rook.

(1p) Verf die door kunstschilders gebruikt wordt, kan worden gemaakt door het mengen van olie, een pigment en een vulstof. Pigmenten zijn vaste stoffen die kleur aan de verf geven. Welk soort mengsel is de beschreven verf? Kies uit: een emulsie, een oplossing, een suspensie en een legering.

(1p) Een leerling voegt een kleurloze oplossing van ammoniak toe aan een oplossing van lood(II)nitraat. Hierbij verandert de stof van kleurloos en helder naar wit en troebel. Is het mengsel dat is ontstaan een oplossing of niet? Leg je antwoord uit.
(Bron: Examen VMBO-T, 2021-1)

(1p) Een leerling voegt ammoniak toe aan een oplossing van koper(II)sulfaat. In dit geval verandert de stof van lichtblauw en helder naar donkerblauw en helder. Is het mengsel dat is ontstaan een oplossing of niet? Leg je antwoord uit.
(Bron: Examen VMBO-T, 2021-1)

(3p) Vul de volgende tabel in:

Vaste stof Vloeistof Gas

In vaste stof

In vloeistof

In gas

§3 Concentratie

In deze paragraaf gaan we leren rekenen met het begrip concentratie. Een bekend voorbeeld waarbij concentratie een rol speelt is limonade. Hoe meer siroop er in een bepaalde hoeveelheid water wordt gedaan, hoe hoger de concentratie.

Als we twee stoffen met elkaar mengen, dan kunnen we dit in verschillende verhoudingen doen. Denk bijvoorbeeld aan limonade. We kunnen zelf kiezen hoeveel siroop en hoeveel water we toevoegen bij het maken van limonade. De hoeveelheid water en de hoeveelheid siroop bepalen samen hoe zoet de limonade zal smaken. Als de limonade erg zoet is, dan spreken we van een hoge concentratie siroop. Als je de siroop bijna niet proeft, dan spreken we van een lage concentratie siroop.

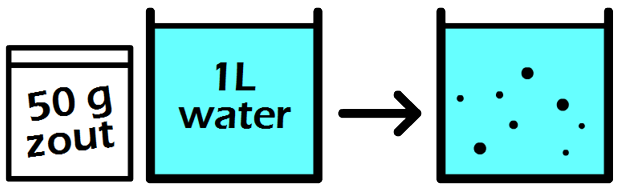
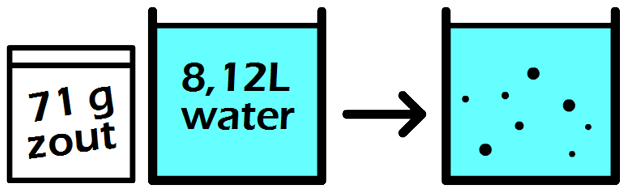
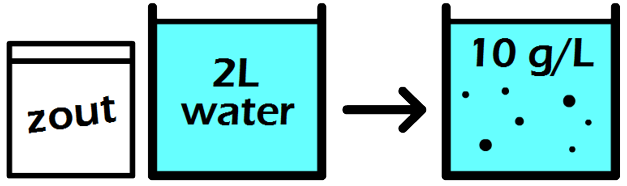
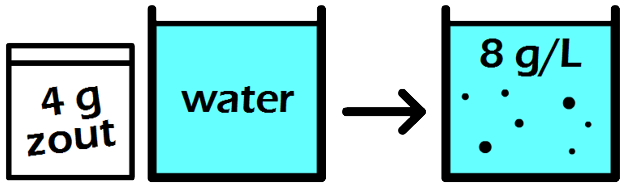
In de onderstaande afbeelding zien we een maatkolf. Stel we schenken 24 gram siroop in de maatkolf en vullen dit daarna aan met water tot aan de stippellijn. Zoals aangegeven op de maatkolf, hebben we dan 1000 mL (1,000 L) limonade. De limonade die we nu gemaakt hebben, heeft een siroopconcentratie van 24 gram per liter (24 g/L).

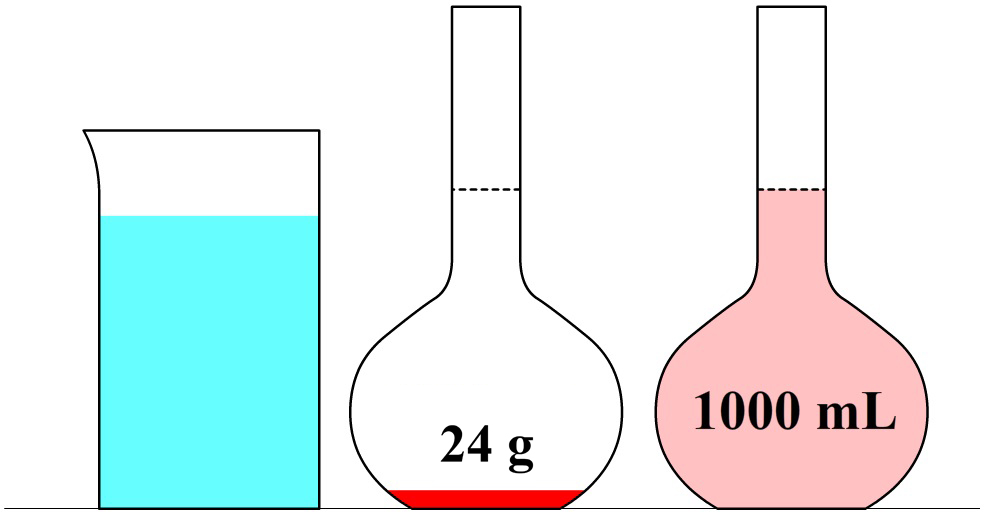
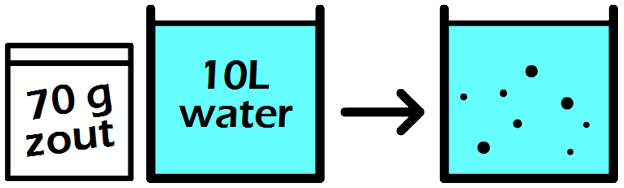
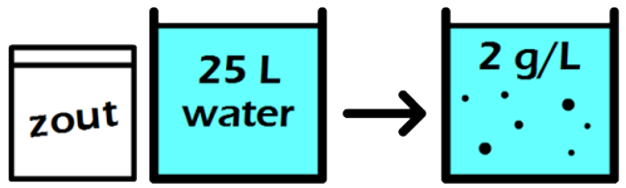
In de volgende maatkolf schenken we 24 gram siroop in een maatkolf en vullen dit aan tot we 2000 mL (2,000 liter) limonade hebben. Elke liter limonade bevat in dit geval dus 24 / 2 = 12 gram siroop. De siroopconcentratie is in dit geval dus 12 g/L. In dit tweede voorbeeld is de siroopconcentratie dus lager en als gevolg smaakt de limonade minder zoet.

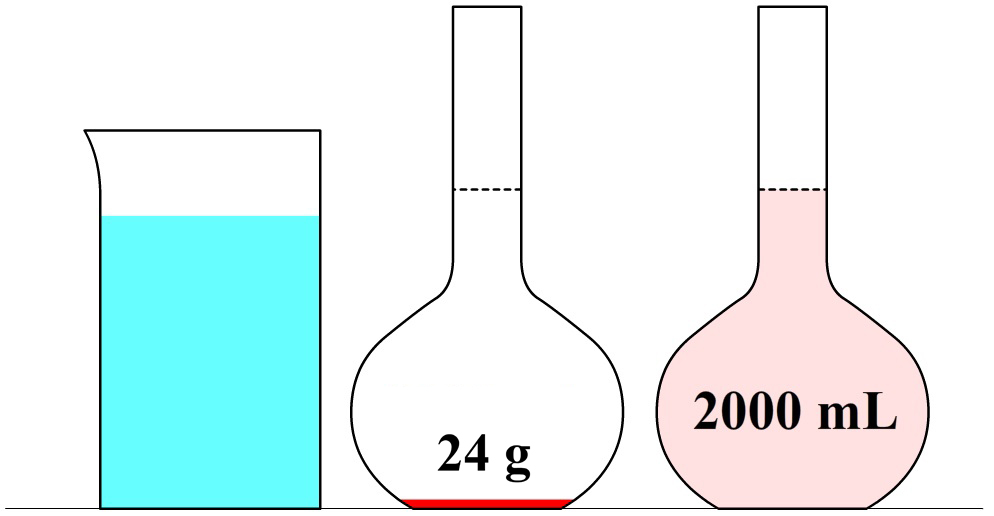
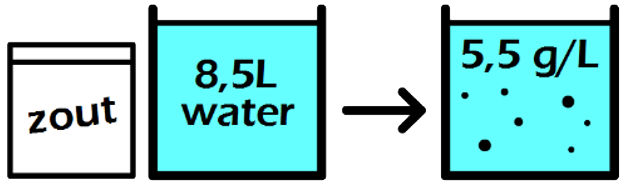
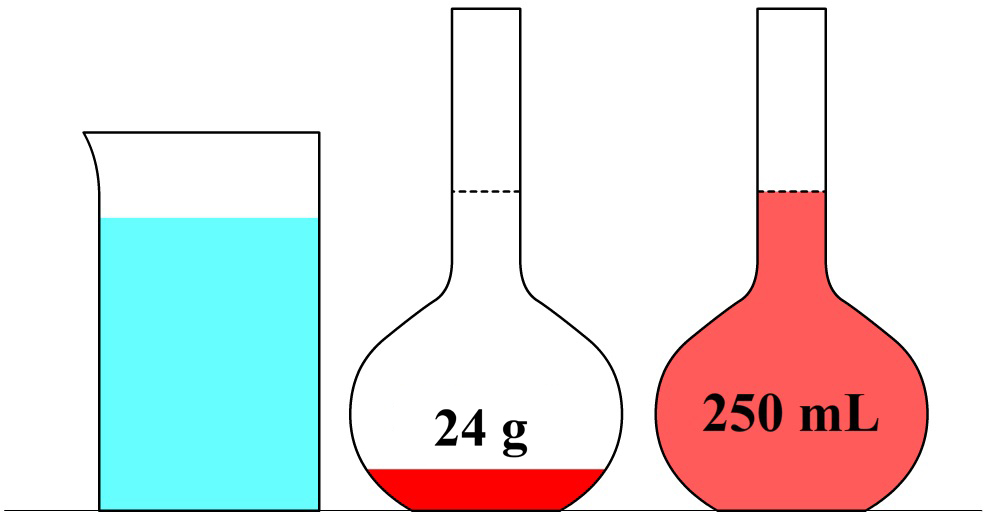
In de volgende maatkolf schenken we 24 gram siroop in een maatkolf en vullen dit aan tot we 250 mL (0,25 liter) limonade hebben. In dit geval zou een liter van deze limonade 24 × 4 = 96 gram siroop bevatten. Deze limonade heeft dus een siroopconcentratie van 96 g/L. In dit voorbeeld is de concentratie dus hoger en smaakt de limonade dus zoeter.

Voorbeeld

Vraag:

Een leerling maakt eerst 1,2 L limonade met daarin 10 gram siroop en daarna ook nog 0,15 L limonade met daarin 2,0 gram siroop. Welke limonade smaakt zoeter?

Antwoord:

We kunnen deze vraag beantwoorden door de gegevens te noteren in een verhoudingstabel. De eerste soort limonade bevat 10 gram siroop en heeft een volume van 1,2 liter. Als we de concentratie van deze limonade willen weten, dan willen we weten hoeveel gram siroop er in 1 liter van deze limonade opgelost is:

Massa siroop 10 g ... g

Volume limonade 1,2 L 1 L

De gemakkelijkste manier om dit soort problemen op te lossen is door kruislings te vermenigvuldigen. Je vermendigvuldigt in dat geval de twee getallen die diagonaal genoteerd zijn en daarna deel je door het overgebleven getal. In de instructiefilmpjes bij deze paragraaf wordt deze techniek uitgebreid uitgelegd. We vinden hiermee:
$$ \frac{10 \times 1}{1,2} = 8,3 \text{ g} $$
Dit antwoord vullen we in de verhoudingstabel in:

Massa siroop 10 g 8,3 g

Volume limonade 1,2 L 1 L

Deze limonade heeft dus een concentratie van 8,3 g/L.

Op dezelfde manier vinden we de concentratie van de tweede limonade. Hier hadden we 2,0 gram siroop in 0,15 liter limonade. De concentratie wordt hiermee:

Massa siroop 2 g 13 g

Volume limonade 0,15 L 1 L

Deze limonade heeft dus een concentratie van 13 g/L.

Met deze gegevens zijn we in staat de vraag te beantwoorden. Omdat de tweede limonade een hogere concentratie heeft, smaakt deze limonade het zoetst.

Voorbeeld

Vraag:

Een leerling maakt 2,5 L limonade met een concentratie van 34 g/L. Hoeveel gram siroop is er gebruikt om deze limonade te maken?

Antwoord:

Een siroopconcentratie van 34 g/L betekent dat er 34 gram siroop gebruikt is voor één liter van deze limonade. Door kruislings te vermenigvuldigen vinden we dan voor 2,5 liter limonade:

Massa siroop 34 g 85 g

Volume limonade 1 L 2,5 L

Er is dus 85 gram siroop gebruikt voor de 2,5 L limonade.

Voorbeeld

Vraag:

Een leerling voegt 35,0 mL siroop met een massa van 40,0 gram bij 200,0 mL water voor het maken van limonade. Bereken de concentratie van de siroop in de limonade.

Antwoord:

Het volume van de limonade bestaat uit het volume van de siroop (35,0 mL) plus het volume van het water (200,0 mL). Het totale volume van de limonade is dus 200,0 + 35,0 = 235,0 mL. Dit komt overeen met 0,2350 L. Hierin zit 40,0 g siroop opgelost.

We willen de concentratie weten. Dit is de hoeveelheid gram per liter. We vinden dit met een verhoudingstabel:

Massa siroop 40,0 g 170 g

Volume limonade 0,2350 L 1 L

De concentratie is dus 170 g/L.

Als laatste bespreken we een examenvraag. De vragen over concentratie behoren geregeld tot de wat lastigere vragen uit het examen. Rustig lezen helpt bij dit soort vragen.

Voorbeeld

Vraag:

Om op de maan te leven zouden we zuurstof uit maansteen (regoliet) kunnen halen. Een astronaut gebruikt gemiddeld 550 liter zuurstof per dag. Bereken hoeveel kilogram regoliet minimaal nodig is om 550 liter zuurstof te produceren. Neem aan dat zuurstof een dichtheid heeft van 1,43 g per liter en dat per gram regoliet 0,42 gram zuurstof kan worden gevormd.
(Bron: Examen VMBO-T, 2023-1)

Antwoord:

Laten we de gegevens eerst even op een rij zetten:

- Een astronaut heeft 550 liter zuurstof per dag nodig.
- Zuurstof heeft een dichtheid van 1,43 gram per liter.
- Er kan 0,42 gram zuurstof gevormd worden met één gram regoliet.

We willen weten hoeveel kilogram regoliet nodig is om genoeg zuurstof te produceren voor de astronaut. Laten de eerst naar de eerste twee gegevens kijken. Elke liter zuurstof heeft een massa van 1,43 gram. We kunnen hiermee uitrekenen hoeveel de massa is van de 550 liter zuurstof die de astronaut nodig heeft:

Massa zuurstof 1,43 g 786,5 g

Volume zuurstof 1 L 550 L

Er is dus in totaal 786,5 gram zuurstof per dag nodig voor de astronaut.

Nu gebruiken we het derde gegeven. Er kan 0,42 gram zuurstof gevormd worden met één gram regoliet. We kunnen hiermee uitrekenen hoeveel gram regoliet er nodig is voor 786,5 gram zuurstof:

Massa zuurstof 0,42 g 786,5 g

Massa regoliet 1 g 1872,6 g

Er is dus 1872 g regoliet per dag nodig om genoeg zuurstof te produceren voor een astronaut. Let er op dat in de vraag staat dat we de massa in kilogram willen weten. Omgeschreven naar kilogrammen is dit afgerond 1,9 kg.

Leerdoelen:

Zorg dat je weet dat concentratie o.a. gemeten wordt in g/L. Dit is de hoeveelheid gram van een stof die in een liter van een mengsel is verwerkt.

Zorg dat je met een berekening de concentraties van mengsels kan vergelijken. De limonade met de grootste concentratie is het zoetst.

Zorg dat je kruislings kan vermenigvuldigen.

Opdrachten

Een leerling lost een schepje zout op in een glas water.

(1p) Hebben we hier te maken met een homogeen of een heterogeen mengsel?

(1p) Ze laat het glas met de oplossing in de zon staan en het water verdampt langzaam. Leg uit hoe de concentratie van de oplossing verandert.

(1p) Een leerling heeft een glas met 200 mL limonade gemaakt. Ze drinkt een kwart van de limonade op. Leg uit of de concentratie van de oplossing hierdoor verandert.

(1p) We doen 50 gram zout in een bak met daarin 1 liter water. Bereken de concentratie. Ga ervan uit dat het volume van de oplossing nauwelijks is toegenomen door het zout.

(1p) We doen 70 gram zout in 10 liter water. Bereken de concentratie van de oplossing. Ga ervan uit dat het volume van de oplossing nauwelijks is toegenomen door het zout.

(1p) We doen 71 gram zout in 8,12 liter water. Bereken de concentratie. Ga ervan uit dat het volume van de oplossing nauwelijks is toegenomen door het zout.

(1p) We doen zout in een bak met 2 liter water totdat de concentratie 10 g/L is. Bereken hoeveel gram zout we nodig hebben. Ga ervan uit dat het volume van de oplossing nauwelijks is toegenomen door het zout.

(1p) We doen zout in een bak met 25 liter water totdat de concentratie 2 g/L is. Bereken hoeveel gram zout we nodig hebben. Ga ervan uit dat het volume van de oplossing nauwelijks is toegenomen door het zout.

(1p) We doen zout in een bak met 8,5 liter water totdat de concentratie 5,5 g/L is. Bereken hoeveel gram zout we nodig hebben. Ga ervan uit dat het volume van de oplossing nauwelijks is toegenomen door het zout.

(1p) Er wordt 4 gram zout in een bak water opgelost. De concentratie wordt 8 g/L. Bereken liter water er in de bak zat. Ga ervan uit dat het volume van de oplossing nauwelijks is toegenomen door het zout.

(1p) Er wordt 342 gram zout in een bak water opgelost. De concentratie wordt 80 g/L. Bereken liter water er in de bak zat. Ga ervan uit dat het volume van de oplossing nauwelijks is toegenomen door het zout.

(1p) Een leerling maakt een zoutoplossing met een concentratie van 5,0 g/L. Bereken hoeveel gram zout er in 8,0 liter van deze oplossing zit.

(2p) Een leerling heeft 250 mL afwaswater nodig met een wasmiddelconcentratie van 20 g/L. Bereken hoeveel gram afwasmiddel de leerling nodig heeft.

(2p) In 1,0 L sodaoplossing is 295 gram soda opgelost. Bereken hoeveel gram soda is opgelost in 8 mL van deze oplossing.

(1p) Een leerling maakt een zoutoplossing van 200 mL, waar 60 gram zout in is opgelost. Bereken hoeveel gram keukenzout je in 450 mL moet oplossen om een even grote concentratie te krijgen.

(2p) Een leerling mengt 20 gram siroop met een volume van 15 mL met 150 mL water. Wat is de concentratie van de limonade?

(2p) Een leerling mengt 60 mL azijn met een halve liter water. De azijn bevat 4,0 g opgelost azijnzuur. Bereken de azijnzuurconcentratie in de gemaakte oplossing.

(2p) Een leerling mengt 60 mL azijn met een 200 mL water. Azijn bevat 40 mg opgelost azijnzuur per mL. Bereken de azijnzuurconcentratie in de gemaakte oplossing.

(3p) Een fles gootsteenontstopper heeft een inhoud van 750 mL. De oplossing bevat 4,12 mg natriumhydroxide per mL. De actieve deeltjes in natriumhydroxide zijn de zogenaamde hydroxide-ionen. In elke 1,75 gram natriumhydroxide is 1,00 gram hydroxide-ionen aanwezig. Bereken hoeveel gram hydroxide-ionen er in de fles zit.

(3p) Een drinkwaterbedrijf produceert 2,5 × 10¹⁰ L drinkwater per jaar. Bij het zuiveren wordt de concentratie ijzer in het water verlaagd van 6,1 mg/L naar 0,1 mg/L. Bereken hoeveel kg ijzer minimaal per jaar verwijderd wordt.
(Bron: Examen VMBO-T, 2023-1)

(3p) Om op de maan te leven zouden we zuurstof uit maansteen (regoliet) kunnen halen. Een astronaut gebruikt gemiddeld 550 liter zuurstof per dag. Bereken hoeveel kilogram regoliet minimaal nodig is om 550 liter zuurstof te produceren. Neem aan dat zuurstof een dichtheid heeft van 1,43 g per liter en dat per gram regoliet 0,42 gram zuurstof kan worden gevormd.

(Bron: Examen VMBO-T, 2023-1)

§4 Significante cijfers

In deze paragraaf bespreken we hoe we afronden in de natuur- en scheikunde. Dit doen we met behulp van significante cijfers.

In de natuurkunde en de scheikunde werken we met metingen en metingen zijn vaak onnauwkeurig. Het ligt daarom voor de hand dat we cijfers in de natuurkunde afronden op basis van de nauwkeurigheid van de meting. Hoe nauwkeuriger de meting is, op hoe meer getallen we de meetwaarde afronden.

Neem bijvoorbeeld het potlood in de volgende afbeelding. De meeste mensen zullen waarschijnlijk zeggen dat dit potlood een lengte van 11 cm heeft. We kunnen de lengte van het potlood echter nauwkeurig genoeg aflezen, dat we zeker weten dat het eerste getal achter de komma een nul moet zijn. We zeggen daarom dat de lengte van dit potlood 11,0 cm is. We zien hier dus dat bij natuurkunde en scheikunde de nullen achter de komma van belang zijn!

De cijfers waarin we een meetwaarde mogen noteren noemen we significante cijfers. De meetwaarde 11,0 cm bestaat dus uit drie significante cijfers.

Belangrijk is om te weten dat nullen aan de linkerkant van een meetwaarde niet meetellen als significante cijfers. De meetwaarde 0,0040 meter heeft dus slechts twee significante cijfers.

Er zijn ook getallen in de natuurkunde die wel precies zijn. Neem bijvoorbeeld het aantal leerlingen in een klaslokaal, het aantal ramen in een gebouw, het aantal zijden van een vierkant enzovoorts. We noemen deze precieze getallen telwaarden. Omdat deze waarden precies zijn, hebben ze dus een oneindige hoeveelheid significante cijfers. Als gevolg is het bij berekeningen nooit nodig om naar de significante cijfers van telwaarden te kijken.

Maar wat nu als we een rekensommetje doen met verschillende meetwaarden? Op hoeveel cijfers moeten we het antwoord van dit sommetje dan afronden? De regel is dat we bij vermenigvuldigen en delen het antwoord schrijven in evenveel significante cijfers als de meetwaarde met het minst aantal significante cijfers.

Laten we een voorbeeld bespreken. Stel een leerling heeft een limonade gemaakt met een volume van 4,510 L met daarin 358 gram siroop en we willen de concentratie uitrekenen. 4,510 heeft vier significante cijfers en 358 heeft er drie. Drie significante cijfers is het minst, dus we willen het antwoord ook op drie significante cijfers afronden. De verhoudingstabel komt er zo uit te zien:

Massa siroop	358 g	... g
Volume limonade	4,510 L	1 L

Als we de concentratie op onze rekenmachine berekenen, dan vinden we:

$$ \text{concentratie} = \frac{358 \times 1}{4,510} = 79,3791574279 \text{ g/L}$$

De 1 L is hier een telwaarde en daar hoeven we dus niet bij stil te staan.

Op drie significante cijfers afgerond wordt dit:

$$ \text{concentratie} = 79,4 \text{ g/L}$$

Nog een voorbeeld. Stel we voegen 3000 mg zoutzuur toe aan in 2,0 L water en we willen de concentratie weten in mg/L. 3000 heeft vier significante cijfers en 2,0 heeft er twee. Twee significante cijfers is het minst, dus we willen het antwoord ook op twee cijfers afronden. De verhoudingstabel komt er zo uit te zien:

Massa siroop	3000 mg	... mg
Volume limonade	2,0 L	1 L

Als we de concentratie op onze rekenmachine berekenen, dan vinden we:

$$ \text{concentratie} = \frac{3000 \times 1}{2,0} = 1500 \text{ mg/L} $$

Maar hoe noteren we het getal 1500 in slechts twee cijfers? Dit doen we met behulp van machten van tien. We schrijven:

$$ \text{concentratie} = 1,5 \times 10^3 \text{ mg/L} $$

Machten van tien werken als volgt. 1,5 × 10³ is gelijk aan 1500. Als we een waarde vermenigvuldigen met 10³, dan schuift de komma dus drie plaatsen op naar rechts. Het getal 15 × 10^-2 is gelijk aan 0,15. Als we een waarde vermenigvuldigen met 10^-2, dan schuift de komma dus twee plaatsen op naar links.

In de praktijk is het bij vermenigvuldigen en delen niet nodig om bij elke rekenstap het antwoord in het juiste aantal significante cijfers te schrijven. Bij het eindantwoord is dit echter wel verplicht! Als je het eindantwoord gevonden hebt, kijk dan terug in de vraag naar alle meetwaarden die je gebruikt hebt en ook naar de waarden uit BINAS die je gebruikt hebt en kijk welke waarde het minst aantal significante cijfers heeft. Schrijf je antwoord dan ook in dit aantal significante cijfers op.

Voor optellen en aftrekken bestaat een andere regel. We kijken nu naar het aantal cijfers achter de komma van de gebruikte meetwaarden. We schrijven het antwoord op in evenveel cijfers achter de komma als de meetwaarde met het minst aantal cijfers achter de komma. Stel dat we bijvoorbeeld 15,3 meter optellen bij 0,32 meter, dan vinden we:

$$ 15,3 + 0,32 = 15,62 \text{ m} $$

15,3 heeft slechts één cijfer achter de komma en 0,32 heeft er twee. Eén cijfer achter de komma is het minste, dus we schrijven het antwoord ook maar met één cijfer achter de komma:

$$ 15,3 + 0,32 = 15,6 \text{ m} $$

Let er wel op dat je de waarden eerst omschrijft naar dezelfde eenheid en met dezelfde tienmacht.

Naast machten van tien is het soms ook mogelijk om voorvoegsels te gebruiken. Ook deze kan je in BINAS terugvinden. In de onderstaande tabel staan een aantal belangrijke voorvoegsels:

M	mega	10⁶
k	kilo	10³
m	milli	10^-3
μ	micro	10^-6

Met voorvoegsels kunnen we een meetwaarde als 3,45 × 10^-6 m bijvoorbeeld ook schrijven als 3,45 μm.

↓ VMBO VERSIES van deze VIDEOS komen binnenkort online!

INSTRUCTIE:
Significante cijfers

Leerdoelen:

Zorg dat je het aantal significante cijfers van een meetwaarde kan achterhalen. Denk eraan dat nullen aan de linkerkant niet meetellen.

Zorg dat je telwaarden kan onderscheiden van andere meetwaarden. Bij telwaarden let je niet op significantie.

Zorg dat je waarden kan omrekenen met zowel positieve als negatieve machten van tien.

Zorg dat je waarden in een aantal significante cijfers kan omschrijven met behulp van tienmachten.

Zorg dat je weet dat bij vermenigvuldigen en delen het antwoord wordt geschreven in evenveel significante cijfers als de meetwaarde met het minste aantal significante cijfers.

Zorg dat je weet dat bij optellen en aftrekken het antwoord wordt geschreven in evenveel cijfers achter de komma als de meetwaarde met het minste aantal cijfer achter de komma.

Zorg dat je de voorvoegsels mega, kilo, milli en micro kan gebruiken.

Opdrachten

(6p) Noteer het aantal significante cijfers van de volgende meetwaarden:

25,0 kg/m³

35600 g

12 mg/L

0,350 L

0,000001 m

1,000001 m

(6p) Geef het aantal significante cijfers of geef aan dat er sprake is van een telwaarde:

Een baksteen heeft een massa van 1 kg.

De woonkamer heeft 3 grote ramen.

Er stromen per seconde 900 000 ladingen door de draad.

Er stromen per seconde 900 × 10³ ladingen door de draad.

De spanning van het stopcontact is gelijk aan 230 V.

(8p) Na een berekening geeft je rekenmachine de volgende waarden aan. Schrijf ze in de aangegeven hoeveelheid significante cijfers:

Schrijf 2500 in twee significante cijfers.

Schrijf 0,0150 in twee significante cijfers.

Schrijf 150 in één significant cijfer.

Schrijf 3400,8 in drie significante cijfers.

Schrijf 1 500 000 in vier significante cijfers.

Schrijf 0,00500000 in één significant cijfer.

Schrijf 150 × 10³ in twee significante cijfers.

Schrijf 1800 × 10^-5 in twee significante cijfers.

(2p) Geef het volume van het water in de onderstaande maatcilinder in het juiste aantal significante cijfers.

Bereken de volgende opdrachten in het juiste aantal significante cijfers:

(2p) Een glas limonade heeft een siroopconcentratie van 50 g/L. Er zit 250 mL limonade in het glas. Bereken hoeveel milligram siroop aan de limonade is toegevoegd.

(2p) Een leerling voegt 400,0 mg zwavelzuur toe aan 0,55 L water. Bereken de concentratie in mg/L. Neem aan dat het volume gelijk blijft.

(3p) Een leerling voegt 0,050 mg zwavelzuur toe aan water. De oplossing die hierbij ontstaat heeft een volume van 40,0 mL. Bereken de concentratie in μg/L.

(2p) Een leerling mengt 25,5 mL siroop met 1501,75 mL water. Bereken het volume van de limonade.

(3p) Een leerling mengt 15 mL siroop (20,0 gram) met 150 mL water. Bereken de concentratie van het water.

(1p) Een vaccin bevat onder meer de volgende bestanddelen: 0,86 mg aluminiumhydroxide, 50 μg conserveringsmiddel, 50 mg sucrose en 17 μg (verzwakte) ziekteverwekker. Van welk van de gegeven bestanddelen bevat het vaccin de grootste massa?
(Bron: Examen VMBO-T, 2023-1)

§5 Volume- en massaprocent

In deze paragraaf gaan we leren concentraties weer te geven als procenten. Dit kan op twee manieren: met massaprocent en met volumeprocent.

Tot nu toe hebben we concentraties weergegeven in gram per liter. We kunnen concentraties echter ook weergeven in procenten. Er zijn twee manieren waarop we dit kunnen doen.

Kijk bijvoorbeeld eens naar de rechter afbeelding. We zien een mengsel bestaande uit rode en gele deeltjes. Hieronder bereken we welk percentage van het volume van het mengsel uit gele deeltjes bestaat. Het totale volume van het mengsel is 4 L en het volume van de gele deeltjes is 1 L. Hiermee vinden we:

Volume	4 L	1 L
Volumeprocent	100 vol%	25 vol%

We zeggen dan dat de concentratie 25 volumeprocent is. We korten dit meestal af tot 25 vol%.

Naast het volume kunnen we ook naar de massa kijken. Stel we willen weten welk percentage van de massa van het mengsel uit gele deeltjes bestaat. De totale massa van het mengsel is 10 kg en dit stellen we gelijk aan 100%. De massa van de gele deeltjes is 4 kg. Hiermee vinden we:

Massa	10 kg	4 kg
Massaprocent	100%	40%

We zeggen dan dat de concentratie 40 massaprocent is. Afgekort schrijven we dit gewoon op als 40%.

Zoals je in dit voorbeeld kan zien, kan voor hetzelfde mengsel het volumepercentage (25 vol%) en het massapercentage (40%) verschillen.

       Voorbeeld

Vraag:

1,50 liter wijn bevat 12,0 vol% alcohol. Bereken hoeveel milliliter alcohol er in de fles zit.

Antwoord:

Hiervoor gebruiken we weer een verhoudingstabel. Het totale volume van de wijn is 1,50 L. Dit komt dus overeen met 100 vol%:

Volume 1,50 L     0,180 L

Volumeprocent 100 vol%     12,0 vol%

De fles bevat dus 0,180 L alcohol. In de vraag staat dat we het volume willen weten in milliliter. 0,180 L is gelijk aan 180 mL.

De gegevens in de vraag hebben elk drie significante cijfers. Het is dus juist dat het antwoord ook in drie significante cijfers geschreven is.

       Voorbeeld

Vraag:

Aan 120 mL water is 8 mL siroop toegevoegd. Bereken de siroopconcentratie in volumeprocent.

Antwoord:

We hebben in totaal 120 + 8 = 128 mL limonade. Dit is het totale volume, oftewel 100 vol%. We willen weten hoeveel volumeprocent bestaat uit siroop. Als we de verhoudingstabel invullen, vinden we:

Volume 128 mL     8 mL

Volumeprocent 100 vol%     6,25 vol%

De siroopconcentratie is afgerond 6 vol%.

We kijken nog even naar de significantie. In de verhoudingstabel gebruiken we 8 mL in een vermenigvuldiging. Deze waarde heeft maar één significant cijfer. Vandaar dat we het antwoord hebben afgerond op één significant cijfer.

Voorbeeld

Vraag:

In 250 gram halvarine zit 40% vet. Bereken hoeveel kilogram vet er in de halvarine zit.

Antwoord:

We lossen dit weer op met een verhoudingstabel. De totale massa is 250 gram en komt overeen met 100%:

Massa 250 g 100 g

Massaprocent 100% 40%

Er zit dus 100 gram vet in de halvarine. In de vraag staat dat we het antwoord willen weten in kilogram. 100 gram is gelijk aan 0,10 kg.

Het gegeven met het minst aantal significante cijfers is 40%. Dit heeft twee significante cijfers. Het antwoord is dus ook in twee significante cijfers geschreven. Nullen aan de linkerzijde tellen niet mee. Vandaar dat het antwoord geschreven is als 0,10 kg.

Leerdoelen:

Zorg dat je kan rekenen en redeneren met massaprocent en volumeprocent

Opdrachten

(1p) Op een zak chips staat: "Light chips met slechts 4% vet". Wat betekent deze 4% precies?

Op een bierflesje Rochefort 10 staat 11,3% VOL.

(1p) Leg uit wat dit betekent.

(2p) Het volume van de fles is 33 cL. Bereken hoeveel milliliter van het biertje bestaat uit alcohol. Denk bij deze en alle volgende vragen aan significantie.

(2p) In 450 gram jam zit 160 gram suiker. Bereken de suikerconcentratie van deze jam in massaprocent.

(2p) Een leerling lost 4 gram zout op in een bak met 46 gram water. Bereken de zoutconcentratie in massaprocent?

(4p) In 80 gram sodaoplossing is 15 gram soda opgelost. Een leerling verdunt deze oplossing met 120 g water. Bereken de sodaconcentratie in zowel de oorspronkelijke als de verdunde oplossing. Druk de concentratie uit in massaprocent.

(2p) Een gouden medaille voor de Olympische Spelen 2020 weegt 556 gram en bevat 1,08 massaprocent goud. Ga na hoeveel gram goud er in de medaille verwerkt is.

Plantaardige alternatieven voor roomboter zijn bijvoorbeeld margarine en halvarine. Margarine bestaat voor ongeveer 80 volumeprocent uit oliën, halvarine maar voor 40 volumeprocent. Beide producten bestaan verder voornamelijk uit water. Olie en water mengen slecht en daarom is een hulpstof toegevoegd die voorkomt dat de stoffen ontmengen. Tijdens een practicum smelten leerlingen een hoeveelheid margarine. Hierbij gebruiken ze de opstelling die is weergegeven in de twee onderstaande afbeeldingen. Zoals je kunt zien wordt de margarine hier gesmolten in een bak met verwarmd water. Wanneer de margarine volledig is gesmolten, zijn lagen ontstaan (zie de rechter afbeelding).

(1p) Geef de naam van het soort mengsel dat ontstaat wanneer olie en water worden gemengd.

(1p) Geef de maximale temperatuur die de margarine kan bereiken bij dit onderzoek. Vermeld ook de eenheid.

(1p) De leerlingen smelten halvarine op dezelfde manier als de margarine. Welke van de onderstaande figuren geeft het eindresultaat weer? Leg je antwoord uit.

(Bron: Examen VMBO-T, 2023-2)

(3p) Voor het maken van nylon wordt een mengsel van 200 kg gebruikt. Dit mengsel bestaat voor 3,1 massaprocent uit een zwavelzuuroplossing. Deze oplossing heeft een dichtheid van 1,83 kg/L. Bereken hoeveel liter zwavelzuuroplossing het mengsel bevat.
(Bron: Examen VMBO-T, 2022-1)

(4p) Een fles gootsteenontstopper heeft een inhoud van 750 mL. De oplossing bevat 4,12 mg natriumhydroxide per mL. De actieve deeltjes in natriumhydroxide zijn de zogenaamde hydroxide-ionen. Natriumhydroxide bestaat voor 42,5% uit deze ionen. Bereken hoeveel gram hydroxide-ionen er in de fles zit.