Hoofdstuk 3
Kwantumfysica

§1     Deeltjesverschijnselen

De kwantumfysica geeft ons een zeer nauwkeurige beschrijving van de kleine deeltjes waaruit de wereld bestaat. De eerste doorbraak in deze theorie was Einstein’s ontdekking dat licht uit deeltjes bestaat. Deze deeltjes worden fotonen genoemd. In deze paragraaf gaan we lezen hoe deze ontdekking gedaan is.

Als we licht op metaalatomen schijnen, dan kan dit licht geabsorbeerd worden door de elektronen in deze atomen. In sommige gevallen heeft het licht genoeg energie om elektronen uit de atomen trekken. De elektronen schieten dan weg van de metaalatomen. Dit wordt het foto-elektrisch effect genoemd.

In de 19^de eeuw werd ontdekt dat licht golfeigenschappen heeft. Als gevolg werd gedacht dat het ontsnappen van de elektronen zou moeten afhangen van de intensiteit  (en dus van de amplitude) van deze golven. Volgens deze theorie zou elke kleur licht elektronen moeten kunnen laten ontsnappen uit het metaal, als we het licht maar fel genoeg maken (zie de onderstaande afbeelding).

In werkelijkheid bleek dit echter niet het geval. In plaats van de intensiteit, bleek het de frequentie (en dus de kleur) van het licht het verschil te maken. Als de frequentie boven een bepaalde grensfrequentie (f_grens) komt, dan ontsnappen de elektronen en anders niet. In BINAS vinden we voor verschillende stoffen deze grensfrequentie. Licht dat deze grensfrequentie niet bereikt, zal nooit elektronen doen laten ontsnappen, hoe fel we het licht ook maken.

Einstein concludeerde op basis van deze observatie dat licht behalve golf- ook deeltjeseigenschappen heeft. Volgens Einstein was licht opgebouwd uit kleine deeltjes genaamd fotonen. Als de lichtgolf het metaal raakt, dan is het niet de gehele golf die geabsorbeerd wordt, maar de individuele fotonen waaruit het licht bestaat. Als een enkel foton genoeg energie heeft, dan zal het elektron ontsnappen uit het atoom en anders niet. De intensiteit heeft hier geen invloed op. Hoe hoger de intensiteit, hoe meer fotonen, maar als elk afzonderlijk foton niet genoeg energie heeft, dan zal geen van deze fotonen in staat zijn een elektron te laten ontsnappen.

Max Planck had eerder in een onderzoek aangetoond dat de energie van een foton gelijk is aan:

$$E_{foton} = hf$$ Energie van het foton (Efoton) joule (J) De constante van Planck (h) 6,62606957 × 10-34 Js Frequentie van het foton (f) hertz (Hz)

Met de formule v = fλ uit het hoofdstuk trillingen en golven, kunnen we deze formule herschrijven. Als we voor de snelheid v de lichtsnelheid c gebruiken, dan vinden we:

$$E_f = h\frac{c}{\lambda}$$ Energie (Ef) joule (J) Constante van Planck (h) 6,62606957 x 10-34 Js Lichtsnelheid (c) 2,99792458 x 108 m/s Golflengte van foton (λ) meter (m)

Naast de grensfrequentie bestaat ook de grensgolflengte. Voor een aantal metalen zijn ook deze waarden in BINAS te vinden. Met behulp van de bovenstaande formule kunnen we zien dat een grotere golflengte zorgt voor een kleinere energie. Alleen bij golflengtes kleiner dan de grensgolflengte vindt dus het foto-elektrisch effect plaats.

De energie van fotonen wordt in plaats van joule ook wel in elektronvolt (eV) gegeven. Er geldt:

$$1 \text{ eV} = 1,6022 \times 10^{-19} \text{ J}$$

Bij het foto-elektrisch effect moet het foton in ieder geval genoeg energie hebben om het elektron uit het metaal te trekken. Deze energie wordt de uittree-energie (E_uittree) of ook wel de ionisatie-energie genoemd. De uittree-energie is voor verschillende stoffen in BINAS te vinden. Als er dan nog energie over is, dan wordt deze energie meegegeven aan het elektron in de vorm van kinetische energie. Dit is de energie waarmee het elektron wegschiet uit het materiaal. Er geldt dus:

$$E_{foton} = E_{uittree} + E_{kin} \;\;\; \text{(bij ontsnappen elektron)}$$

Met de onderstaande schakeling kunnen we het foto-elektrisch effect nauwkeuriger bestuderen. Een metalen plaatje (aangegeven met de rode streep) wordt aangesloten op de minpool van een spanningsbron. Een metalen bolletje (het rode stipje) wordt aangesloten op de pluspool. In eerste instantie wordt de spanning op 0 volt gezet. Als we licht op het metalen plaatje schijnen, dan komen er elektronen vrij. Een aantal van de elektronen zal toevallig tegen het metalen bolletje aan de overkant komen (zie afbeelding A). Op deze manier ontstaat een stroom van elektronen die met de ampèremeter kan worden gemeten.

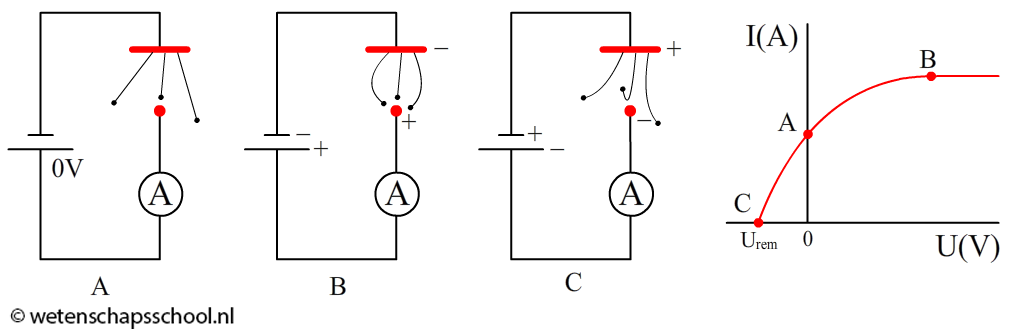
Als we de spanning groter maken dan 0 V, dan wordt het metalen bolletje positief (zie afbeelding B). Dit zorgt ervoor dat de losvliegende elektronen tot het bolletje worden aangetrokken. Er zullen hierdoor meer elektronen aankomen, waardoor de stroomsterkte toeneemt. Als we de spanning blijven verhogen, dan komt er een moment dat alle losgekomen elektronen op het metalen bolletje terecht komen. De stroomsterkte is nu maximaal. Als we de spanning nog hoger zetten, dan zal de stroomsterkte nu niet meer toenemen, omdat alle losgekomen elektronen immers al zijn aangekomen.

We kunnen de spanning ook negatief maken. In dat geval wordt het metalen bolletje negatief. De elektronen die vrijkomen worden hier nu juist door afgestoten (zie afbeelding C). Bij een bepaalde negatieve spanning komt geen enkel elektron meer aan. De stroomsterkte is dan 0 A. De spanning waarbij dit voor het eerst gebeurt, noemen we de remspanning (U_rem). Hoe groter de kinetische energie van de elektronen is, hoe groter de remspanning moet zijn om de elektronen af te remmen. Bij het afremmen wordt de kinetische energie geheel omgezet in elektrische energie.

De formule voor de elektrische energie van een geladen deeltje is:

$$E_{elek} = qU$$ Elektrische energie (Eelek) joule (J) Lading (q) Coulomb (C) Spanning (U) volt (V)

Voor het elektron is de lading (q) gelijk aan de elektronlading (e). De lading is te vinden in BINAS.

Met de bovenstaande formules wordt de energieomzetting van het foto-elektrisch effect:

Met deze formule kunnen we de constante van Planck en de grensfrequentie van verschillende metalen bepalen.

Redeneren en rekenen met het foto-elektrisch effect

Leg uit hoe je met het foto-elektrisch effect kan aantonen dat licht uit fotonen bestaat. In de onderstaande afbeelding zien we het (U,I)-diagram dat gebruikt wordt bij onderzoek naar het foto-elektrisch effect. Leg uit waarom de grafiek uiteindelijk afvlakt. Schets hoe het diagram verandert als je de intensiteit van het licht groter maakt, maar de frequentie van het licht gelijk laat. Schets hoe het diagram verandert als je een metaal kiest met een grotere uittree-energie. Schets hoe het diagram verandert als je de frequentie van het licht groter maakt, maar de intensiteit van het licht gelijk laat. Leg uit hoe je met de grensfrequentie en de grensgolflengte kan bepalen of een metaalatoom zal ioniseren of niet. Ga na of blauw licht sterk genoeg is om elektronen in een stuk zilver te ioniseren. Fotonen met een golflengte van 300 nm worden op een stuk zink geschoten. Leg uit of de elektronen in het zink zullen ioniseren. Een lichtbundel bestaande uit fotonen met een golflengte van 200 nm wordt op een stuk zilver geschoten. De elektronen die hierbij vrijkomen worden afgeremd in een elektrisch veld. De minimale spanning waarbij de elektronen volledig worden afgeremd blijkt 1,5 V te zijn. Bereken met deze gegevens de constante van Planck. Het foto-elektrisch effect wordt vaak aangetoond in een experiment zoals hieronder is weergegeven. In zo'n experiment wordt de kathode in een vacuümbuis beschenen door een laser met een golflengte λ = 410 nm en een vermogen van P = 3,0 mW. Op de kathode komen dan elektronen vrij die naar de anode bewegen. De stroomsterkte I in de kring wordt uitgezet tegen de spanning U. Bij welke spanning komen alle elektronen aan bij de anode? Waarom bereiken bij een lagere spanning niet alle vrijgemaakte elektronen de anode. Zelfs als de fotonen genoeg energie hebben, dan nog maakt niet elk foton dat op een metaal valt een elektron vrij. De fractie van de fotonen dat een elektron vrijmaakt noemen we het kwantumrendement (nQ). Het kwantumrendement is hieronder uitgezet tegen de golflengte van het opvallende licht: Toon aan dat de fotokathode van koper is. Leg uit hoe je op je antwoord komt. (bron: examen 2016 voorbeeldopgaven)

§2     Golfverschijnselen

In de vorige paragraaf hebben we gezien dat licht uit deeltjes bestaat genaamd fotonen. In deze paragraaf gaan we zien dat licht ook golfeigenschappen heeft. Tevens gaan we zien dat ook massieve deeltjes zoals elektronen zowel golf- als deeltjesverschijnselen hebben.

We kunnen als volgt aantonen dat licht ook golfeigenschappen heeft. Als we licht op een plaatje met twee dunne spleetjes schijnen, dan ontstaan achter beide spleet cirkelvormige golven, die met elkaar gaan interfereren (zie de onderstaande afbeelding). We noemen dit het dubbele spleet experiment. Als we achter het scherm een detector plaatsen, dan zien we op dit scherm maxima en minima zoals we dat ook in het hoofdstuk over geluid gezien hebben.

Als licht alleen deeltjeseigenschappen zou hebben, dan hadden we het onderstaande patroon gezien. Licht zou dan slechts op twee plekken op het scherm te zien zijn. Dit is echter niet het geval. Licht gedraagt zich dus duidelijk als een golf in dit experiment. Omdat licht dus zowel deeltjes- als golfeigenschappen heeft, spreken we hier van golf-deeltje-dualiteit.

Later ontdekte men dat deze dualiteit niet alleen geldt voor fotonen, maar voor alle elementaire deeltjes. We kunnen bijvoorbeeld ook elektronen door twee spleten schieten. In de onderstaande afbeelding zien we wat er in dat geval gebeurt. Ten eerste zien we dat de elektronen op specifieke punten op de detector terecht komen. Dit suggereert dat elektronen deeltjes zijn. Maar als we lang genoeg wachten, dan zien we een interferentiepatroon ontstaan. Dit suggereert juist dat elektronen golven zijn. Een dergelijk interferentiepatroon kan alleen ontstaan als elk elektron door beide spleten is gegaan en met zichzelf heeft geinterfereerd! Het moment dat de elektrongolf echter tegen de detector botst, verschijnt het elektron als een puntje op het scherm, alsof het juist een deeltje is! De golf is op dat moment dus ineengeklapt tot een deeltje. Dit lijkt onlogisch, maar toch is dit wat we meten. De bekende kwantumfysicus Niels Bohr zei over deze vreemde effecten: 'wie zegt de kwantumfysica te begrijpen, heeft het niet begrepen'.

Maar wat bepaalt dan waar het elektron terecht komt op de detector? Dit blijkt niet te voorspellen te zijn. Het is niet mogelijk van te voren uit te vinden waar het elektron op het scherm zal komen. Het enige dat we weten, is dat als je genoeg elektronen afschiet, dat dan een voorspelbaar interferentiepatroon ontstaat. Bij de maxima is de kans op een elektron het grootst en bij de minima is er geen kans het elektron te vinden. De kwantumfysica is dus gebaseerd op kans en het interferentiepatroon geeft ons hoe groot deze kans is. We noemen dit patroon daarom ook wel een waarschijnlijkheidsverdeling (P). Hieronder zien we een afbeelding van de waarschijnlijkheidsverdeling die bij dit experiment hoort:

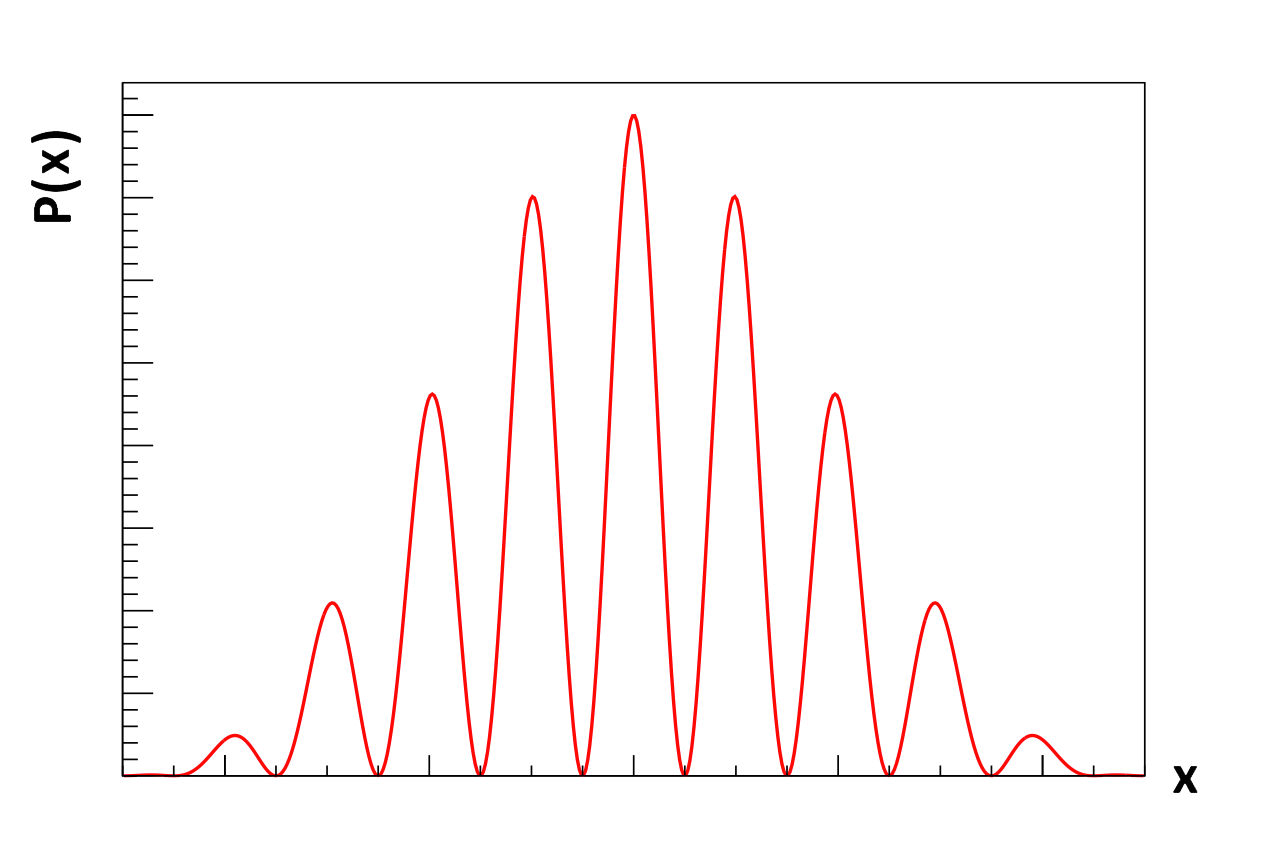
Als je de kans wil vinden dat je een elektron in een bepaald gebiedje zal aantreffen, dan doe je dat door de oppervlakte onder de grafiek te bepalen. Het totale oppervlak onder de grafiek is dus altijd 1, oftewel 100%. Als je overal zoekt, heb je namelijk zekerheid dat je het elektron ergens zal vinden.

Als een elektron dus een golf is, dan moet het ook een golflengte hebben. De wetenschapper Louis de Broglie vond één formule voor de golflengte van alle deeltjes. We noemen dit de debroglie-golflengte. Er geldt:

$$\lambda = \frac{h}{p}$$ De debroglie-golflengte (λ) meter (m) De constante van Planck (h) 6,62606957 × 10-34 Js Impuls (p) kilogram keer meter per second (kgm/s)

De impuls wordt voor deeltjes met massa gegeven door:

$$p = mv$$ Impuls (p) kg m/s Massa (m) kilogram (kg) Snelheid (v) meter per seconde (m/s)

Omdat de impuls zo vaak gebruikt wordt in de kwantummechanica, gaan we formule voor de kinetische energie als volgt omschrijven:

$$E_{kin} = \frac{p^2}{2m}$$ Impuls (p) kg m/s Massa (m) kilogram (kg) Kinetische energie (Ekin) joule (J)

In het dagelijks leven merken we weinig van de golfeigenschappen van deeltjes. Dit komt omdat de constante van Planck (h) in de formule van de Broglie erg klein is. Aan de formule λ = h/p zien we dat de golflengte alleen groot wordt als de impuls (p) erg klein is. Dit gebeurt bijvoorbeeld als we een stof extreem koud maken. In dat geval wordt de snelheid en dus ook de impuls van de deeltjes klein.

De formule van de Broglie speelt o.a. een rol in de microscopie. Om dit te begrijpen moeten we eerst het begrip buiging begrijpen. Golven buigen namelijk om voorwerpen heen. Bij geluid kennen we dit effect allemaal. We kunnen bijvoorbeeld iemand horen die om een hoek staat, omdat het geluid de hoek om buigt.

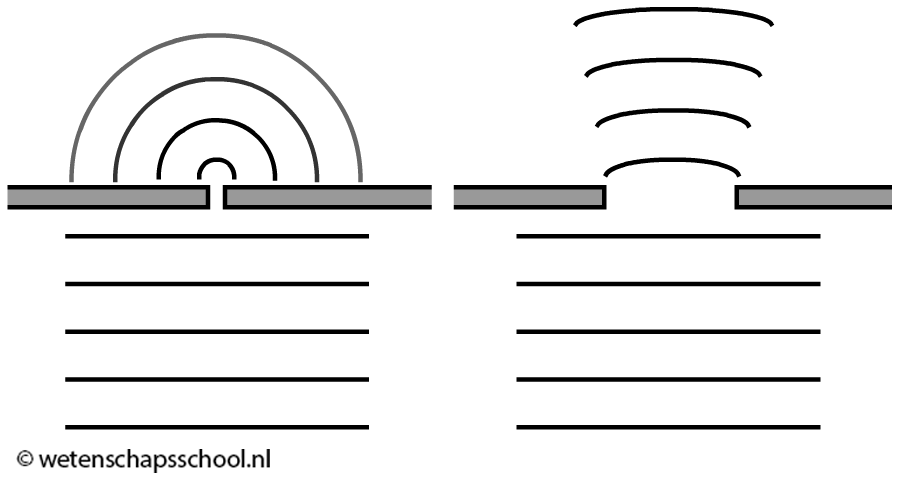
Hieronder zien we golven die zich door een dunne en een brede spleet bewegen. Als de spleet klein is ten opzichte van de golflengte, dan treedt veel buiging op. Zo niet, dan treedt juist weinig buiging op. Bij een erg brede spleet vindt bijna helemaal geen buiging plaats. Dankzij de kleine golflengte van zichtbaar licht, merken we weinig van het buigen van licht in het dagelijks leven. Voor radiogolven is dit echter een ander verhaal. Radiogolven hebben een veel grotere golflengte en buigen daarom gemakkelijk om alledaagse voorwerpen heen. Dit is waarom een radio bijna overal ontvangst heeft. Het radiostraling buigt zich om alle voorwerpen heen en komt zo in alle uithoeken terecht.

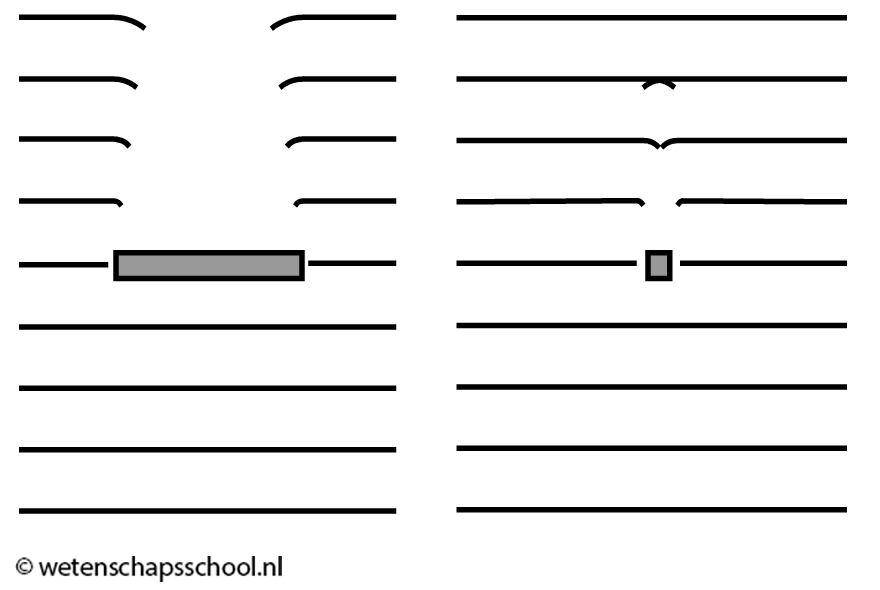
In de onderstaande afbeelding wordt een voorwerp beschenen met licht. Ook hier treedt buiging op. Als het voorwerp klein is ten opzichte van de golflengte, dan treedt veel buiging op. Zo niet, dan vindt weinig buiging plaats. Links in de afbeelding treedt dus weinig buiging op en als gevolg is er achter het voorwerp een duidelijke schaduw te zien. Rechts is de buiging zo extreem dat de golven hun pad vervolgen alsof er helemaal geen voorwerp aanwezig is.

Dit effect zorgt voor een limiet bij het gebruik van lichtmicroscopen. Als de golflengte van zichtbaar licht groter is dan het voorwerp dat je wilt bekijken, dan krijg je door buiging geen goed beeld. Bij erg kleine voorwerpen moet dus een andere type microscoop gebruikt worden. Een voorbeeld is een elektronenmicroscoop. Stel dat de elektronen in dit type microscoop met een snelheid van 2,3 × 10⁵ m/s worden afgeschoten op het voorwerp dat we willen bekijken, dan vinden we de volgende debroglie-golflengte:

Dit is klein genoeg om bijvoorbeeld een virus te kunnen bekijken, hetgeen met een normale microscoop niet mogelijk is.

Redeneren met buiging en interferentie

Als je je hand onder zonlicht houdt, dan ontstaat op de ondergrond een scherpe schaduw. Wat zegt dit over de golflengte van zonlicht? Gebruik in je antwoord het woord buiging. Een paal staat in de zee. Als golven met een golflengte van een paar meter langskomen, dan worden de golven even vervormd door de aanwezigheid van de paal, maar even later gaan de golven verder alsof de paal er niet geweest was. Leg uit hoe dit kan. Leg uit waarom radiogolven geschikt zijn voor het ontvangen van wifi. Leg uit hoe wetenschappers hebben aangetoond dat deeltjes zoals elektronen en fotonen zowel een golf- als een deeltjeskarakter hebben. In de onderstaande afbeelding zien we een golf die aankomt bij een plaat met daarin twee spleten. Achter de spleten ontstaan er bij elke spleet een cirkelvormige golf. Recht achter de twee spleten komen de golven in fase aan. Hier bevindt zich dus een maximum. Het eerst volgende maximum vindt plaats bij punt P. Rechts zien we een close-up van de twee golven die aankomen in punt P. Laat zien dat voor de maxima geldt dat: $$n\lambda = d\sin{\theta}$$ n is hier een heel getal. De afstand tussen de spleten is 1,43 μm. Laat met een bepaling zien dat de golflengte van het licht 567 nm is. Je mag aannemen dat de afbeelding op schaal is afgebeeld. Welke kleur heeft dit licht? Bepaal hoeveel maxima er maximaal achter het scherm te vinden zijn.

Redeneren met de kansverdeling

In de onderstaande afbeelding is schematisch een waterstofjodide-atoom afgebeeld. Het waterstofatoom trilt heen en weer. In de afbeelding zien we een klassieke kansverdeling, waaruit de kans kan worden afgelezen dat het waterstofatoom zich op een bepaalde plek bevindt. Leg uit waarom P(u) een minimum heeft voor u = 0 en een maximum voor u = ±A. Leg uit hoe de waarschijnlijkheidsverdeling P(u) in breedte en hoogte verandert als de totale energie van de trilling groter wordt.

Rekenen met de debroglie-golflengte

Laat met een berekening zien dat een virus van 250 nm niet met zichtbaar licht waargenomen kan worden door een microscoop. Met een elektronenmicroscoop kunnen kleinere voorwerpen zichtbaar worden gemaakt dan met een lichtmicroscoop. Leg uit waarom dit het geval is. Elektronen worden met een snelheid van 2,3 × 105 m/s op een virus geschoten ter grootte van 150 nm. Ga met een berekening na of het mogelijk is om hiermee het virus te bekijken. Bereken of het mogelijk is om met deze microscoop een watermolecuul ter grootte van 0,15 nm zichtbaar te maken. In 1923 deed Louis de Broglie de veronderstelling dat deeltjes een golfkarakter vertonen en dus een golflengte bezitten. In 1927 toonden Clinton Davisson en Lester Germer experimenteel aan dat de veronderstelling van De Broglie juist was. Davisson en Germer gebruikten de opstelling die hieronder schematisch is weergegeven. Weergegeven is een elektronenbundel die versnelt wordt door een versnelspanning U. De bundel komt terecht op een nikkelplaatje. Elektronen die reflecteren tegen het plaatje kunnen worden opgevangen door een detector. Deze kan verdraaid worden rondom het nikkelplaatje. De afstand tussen (het midden van) het plaatje en de detector blijft daarbij gelijk. De detector vangt de elektronen op die terugkomen met een hoek θ ten opzichte van de invallende bundel. Hieronder staan de meetresultaten van dit experiment bij verschillende hoeken. Leg, aan de hand de bovenstaande afbeelding, uit dat elektronen zich hier gedragen als golven. Leg uit of dit patroon ook zichtbaar zou zijn als de elektronenbundel één voor één een elektron zou kunnen afschieten. In de onderstaande afbeelding is schematisch de reflectie van de elektronengolf weergegeven. De punten geven de nikkelatomen weer. De afstand d is de afstand tussen de atomen. De meetresultaten van Davisson en Germer kunnen worden beschreven met: $$n\lambda = d\sin{\theta}$$ n is hier een heel getal. Leid deze formule af. Met de opstelling kan de debroglie-golflengte van de elektronen berekend worden met de formule: $$\lambda = \frac{h}{\sqrt{2meU}}$$ U is hier de versnelspanning. Leid deze formule af met formules uit BINAS. Uit de meetresultaten van Davisson en Germer is de afstand d te bepalen. Bepaal deze afstand. Ga hier uit van een versnelspanning van 54 V. (bron: examen 2016 voorbeeldopgaven) Een onderzoeken schiet positronen op een stuk aluminium. In het metaal worden de positronen afgeremd totdat ze nog een energie van 0,040 eV over hebben. De positronen blijven dan vrij doorbewegen in het metaal, totdat ze botsen tegen elektronen in het metaal. De twee deeltjes annihileren dan en hierbij ontstaan twee fotonen. Hoe lang het duurt voordat het positron annihileert, noemen we de levensduur van het positron. De afstand tussen de atomen in het metaalrooster van aluminium is 0,41 nm. Bereken met hoeveel roosterafstanden de debroglie-golflengte van de vrije positronen in het metaal overeenkomt. (bron: examen 2016 voorbeeldopgaven)

§3     Deeltje in een doos

Om kwantumeffecten beter te begrijpen, bestuderen we in deze paragraaf het simpelste kwantumsysteem: het deeltje in een doos.

In deze paragraaf bestuderen we een deeltje dat alleen naar links en rechts kan bewegen in een afgesloten ruimte (zie de onderstaande afbeelding). We noemen dit het deeltje in een doos.

Als de doos groot is ten opzichte van de kansgolf van het deeltje, dan zal de kansgolf zich als een deeltje gedragen. De kansgolf zal dan heen en weer botsen in het doosje alsof het een deeltje is (zie de onderstaande afbeelding).

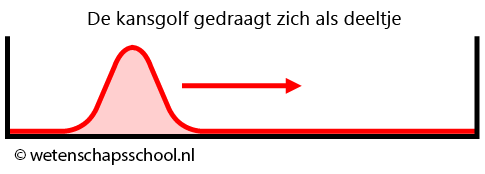
Als de doos echter klein is ten opzichte van de kansgolf, dan beginnen we golfverschijnselen te merken. Als de golf reflecteert tegen de wanden, dan begint deze namelijk met zichzelf te interfereren. Net als bij trillingen in een snaar ontstaat hierbij dan een staande golf met knopen en buiken. Net als bij een snaar geldt dan ook:

In het geval van een deeltje in een doos noemen we n = 1 de grondtoestand en n = 2,3,... de aangeslagen toestanden. n = 2 noemen we de eerste aangeslagen toestand. n = 3 noemen we de tweede aangeslagen toestand. Etc. Hieronder zien we een aantal toestanden van een deeltje in het doosje. Hoe groter de amplitude van de kansgolf, hoe meer kans dat je het deeltje daar zal aantreffen.

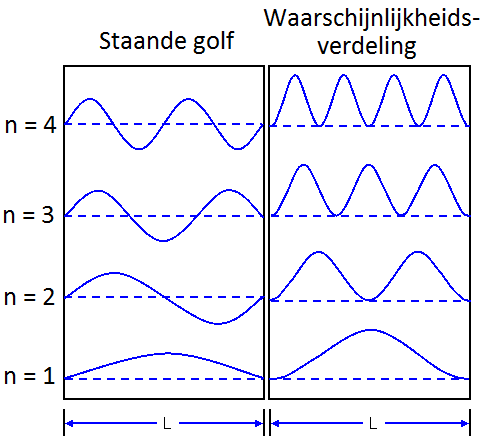
Als we de formule L = ½ λn combineren met λ = h/p, dan vinden we:

Als we deze formule combineren met E_kin = p²/(2m), dan vinden we:

$$E_{kin,n} = \frac{n^2h^2}{8mL^2}$$ Kinetische energie (En) joule (J) Energieniveaus (n) - De constante van Planck (h) 6,62606957 × 10-34 Js Massa van het deeltje (m) kilogram (kg) Lengte van de doos (L) meter (m)

Een aantal dingen kunnen we aan deze formule opmerken. Ten eerste zien we dat het elektron in het doosje niet zomaar elke kinetische energie (en dus niet elke snelheid) kan aannemen. Alleen de waarden die overeenkomen met de staande golven zijn mogelijk. We zeggen daarom dat de energie gekwantiseerd zijn. Merk ook op dat het niet mogelijk is dat het deeltje geen kinetische energie heeft. Zelfs in de grondtoestand n = 1, de laagste toestand, heeft het deeltje namelijk volgens de formule nog gewoon energie. We noemen dit de nulpuntsenergie. Een deeltje in een doos kan dus niet stilstaan!

Als de lengte L van de doos groot wordt, dan kan je aan de formule zien dat de energieniveaus erg dicht op elkaar komen te liggen. Op een gegeven moment komen deze niveaus zo dicht bij elkaar te liggen dat het lijkt alsof het deeltjes gewoon alle energieniveaus kunnen aannemen. Dit is waarom we in het dagelijks leven niks merken van de kwantisering.

Een deeltje in een doosje kan naar een hoger energieniveau springen door o.a. een foton te absorberen met een energie die precies overeenkomt met het verschil tussen het huidige energieniveau en een hoger niveau. Er geldt dus:

$$E_{foton} = \Delta E_n$$ Fotonenergie (Ef) joule (J) Energieverschil tussen twee schillen (ΔE) joule (J)

Dezelfde formule geldt als een elektron terugvalt naar een lager niveau. In dat geval komt er juist een foton vrij. Stel dat een elektron in een doosje met een lengte van 2,0 nm bijvoorbeeld terugvalt van de eerste aangeslagen toestand naar de grondtoestand. Er geldt dan:

Rekenen met een deeltje in een doosje

Leg uit dat het elektron niet stil kan staan in een doosje. Een elektron bevindt zich in een afgesloten ruimte van 200 nm in zijn eerste aangeslagen toestand. Bereken de snelheid van dit elektron. Een elektron bevindt zich in een afgesloten ruimte van 200 nm en beweegt met een snelheid van 9,1 × 103m/s heen en weer. Bereken in welke toestand het deeltje zich bevindt. Leg uit waarom geldt dat 'Ef = ΔEn'. Een foton brengt een proton in een doosje van 300 nm lang van de tweede naar de vierde aangeslagen toestand. Bereken de frequentie van het foton dat hiervoor nodig is. Leg met behulp van een formule uit waarom we er in het dagelijks leven weinig van merken dat elektronen in afgesloten ruimtes slechts bepaalde snelheden kunnen aannemen. Ga naar de website en beantwoord deze vraag met behulp van de animatie. Een elektron in een doosje kan zich ook in meerdere toestanden tegelijk bevinden. In de onderste animatie kan je verschillende toestanden aan en uit zetten. Gebruik deze animatie bij het beantwoorden van de volgende vragen. Een leerling beweert dat de kansgolf niet verandert in de tijd als het elektron zich in slechts één toestand bevindt. Leg uit of de leerling gelijk heeft. Een leerling beweert dat de kansgolf zich meer kan gaan gedragen als een deeltje als het elektron zich in een aantal toestanden tegelijk bevindt. Leg uit wat de leerling hier bedoelt. Met een inktwisser kun je lichtblauwe vulpeninkt onzichtbaar maken door middel van een chemische reactie. Laten we eerst de inktmoleculen bestuderen. Door de inktmoleculen kan één elektron vrij heen en weer bewegen. Het molecuul kan daarom opgevat worden als een energieput met lengte L. De overgang van de grondtoestand van dit elektron naar de eerste aangeslagen toestand komt overeen met de energie van een foton uit het geel-groene deel van het spectrum met een golflengte van 550 nm. Het molecuul absorbeert deze fotonen. De rest van het licht wordt weerkaatst. Als gevolg ziet de inkt er lichtblauw uit. Bereken uit de geabsorbeerde golflengte de lengte van de inktmolecuul. De inktwisser zorgt voor de reactie die hieronder is weergegeven: In het molecuul dat ontstaat, kunnen de elektronen niet meer langs het centrale koolstofatoom bewegen. Hierdoor is de lengte van de energieput gehalveerd. Het energieverschil tussen de grondtoestand en de eerste aangeslagen toestand wordt daardoor 4 keer zo groot. Leg dit uit. Het nieuwe molecuul is kleurloos. Leg dit uit met behulp van een berekening en BINAS. (bron: examen VWO 2016-pilot) Een CD-R is een beschrijfbare CD. Deze CD bestaat uit een gladde laag met daarop een bepaalde kleurstof. Bij een onbeschreven CD-R is deze kleurstoflaag doorzichtig. Als je op één plaats de laag verhit, met een korte laserpuls, wordt de kleurstof op die plaats ondoorzichtig zodat er geen licht meer door kan. Door korte pulsen van de schrijflaser kan informatie zo worden weggeschreven in de vorm van doorzichtige en ondoorzichtige 'spots'. Er wordt gebruik gemaakt van cyanine-kleurstoffen. Hieronder staan een aantal van deze moleculen weergegeven. In zo'n molecuul is steeds een aantal vrije elektronen aanwezig. Deze elektronen zitten opgesloten tussen de eindgroepen. Deze opsluiting is te beschrijven als deeltjes in een eendimensionale energieput met lengte L. In het onderstaande diagram is deze lengte uitgezet tegen het aantal C-atomen in de keten. In de onderstaande afbeelding zijn de energieniveaus van de elektronen bij vijf verschillende ketenlengtes weergegeven. Bij een ketenlengte met 5 C-atomen zijn de niveaus 1, 2 en 3 weggelaten. Bereken de hoogte van de energie van de niveaus 1, 2 en 3 bij een ketenlengte van 5 C-atomen en teken ze in de afbeelding. Absorptie van licht vindt plaats als een elektron in het hoogste gevulde niveau naar een niveau hoger springt. In de bovenstaande afbeelding is dit aangegeven met pijlen. De CD-R heeft een brand-laser met een golflengte van 800 nm. Bepaal met behulp van de afbeelding welk van deze moleculen daarbij het beste als kleurstof kan worden gebruikt. Licht je antwoord toe met een berekening. (bron: examen 2016 voorbeeldopgaven)

§4     Het atoommodel

Met de kwantumfysica kunnen we ook het waterstofatoom beschrijven. In deze paragraaf gaan we zien hoe dit werkt.

De kwantummechanische beschrijving van het waterstofatoom wordt ook wel het atoommodel van Bohr genoemd. Net als in het geval van het deeltje in een doos, kan ook het elektron in een waterstofatoom gezien worden als een staande golf. Ook het elektron in waterstof kan zich in de grondtoestand of één van de aangeslagen toestanden bevinden. In elke toestand bevindt het elektron zich in een andere schil om de kern (zie de onderstaande afbeelding).

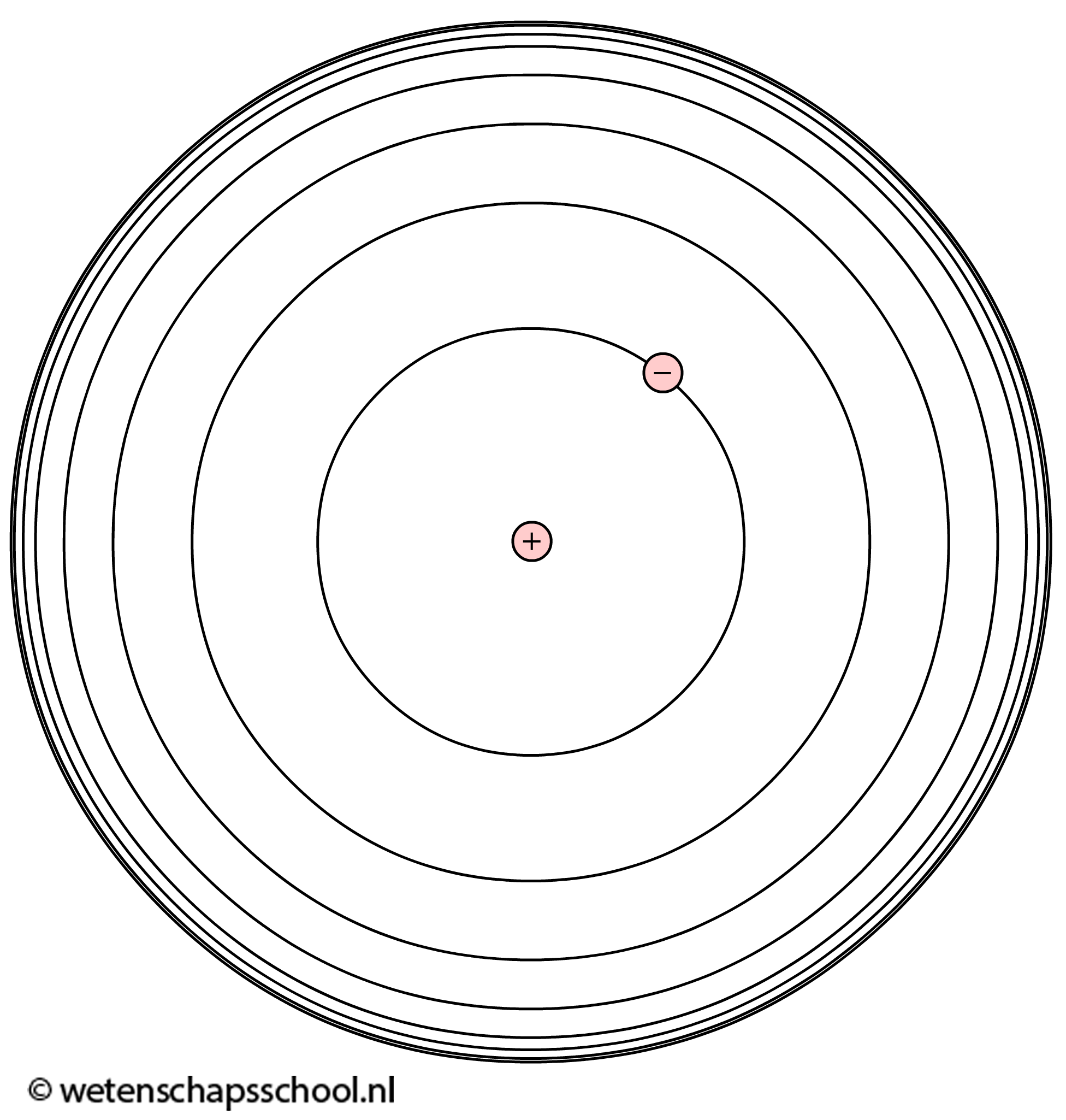
In elke schil heeft het elektron een specifieke energie. Deze energie bestaat uit een combinatie van kinetische en elektrische energie. In een opdracht onder aan deze paragraaf zullen we bewijzen dat de energieniveaus die bij deze toestanden horen gegeven worden door:

$$E_n(\text{eV}) = \frac{-13,6}{n^2} \;\;\;\; \text{(waterstofatoom, energie in eV)}$$ Energie (En) electronvolt (eV) Energieniveau (n) -

Merk op dat de energie in deze formule in elektronvolt is gegeven.De energieniveaus uit de formule zijn hieronder ook schematisch weergegeven. Deze afbeelding is ook te vinden in BINAS.

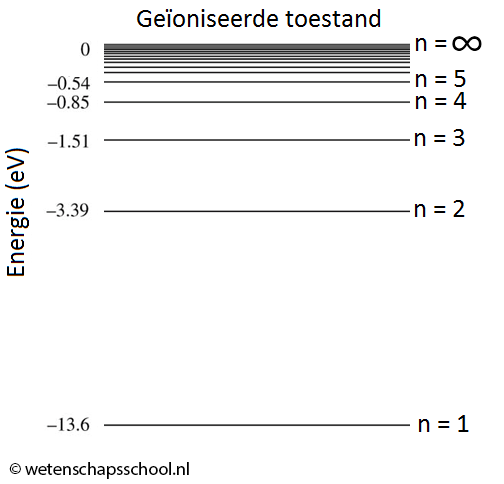
Net als bij het deeltje in het doosje, kan een elektron in waterstof verspringen naar een hoger energieniveau door een foton op te nemen en kan het elektron verspringen naar een lager niveau door dit foton weer uit te zenden. Bij een overgang van n = 3 naar n = 2, komt bijvoorbeeld een foton vrij met de volgende energie:

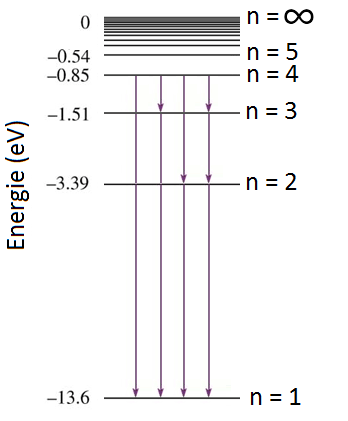
Op den duur valt een aangeslagen elektron helemaal terug naar zijn grondtoestand. Soms gebeurt dit in één stap en soms in meerdere stappen. Hieronder zien we bijvoorbeeld de verschillende manieren waarop een elektron in een waterstofatoom van de derde aangeslagen toestand (n=4) kan terugvallen naar de grondtoestand (n=1).

De fotonen die bij waterstof vrijkomen als elektronen van een willekeurige aangeslagen toestand naar de eerste aangeslagen toestand (n = 2) vallen, behoren tot de zogenaamde Balmerserie (zie de onderstaande afbeelding).

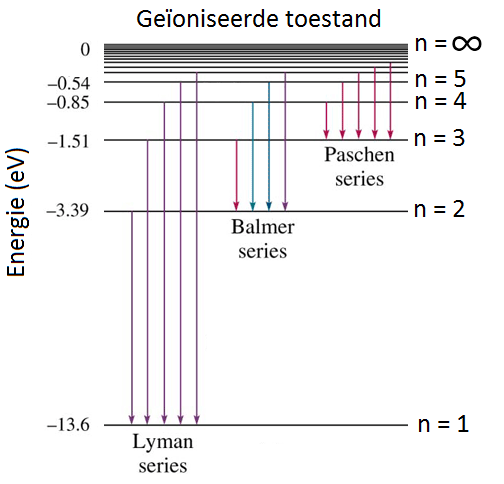
De eerste paar fotonen uit de balmerserie vallen in het zichtbare spectrum. Deze golflengten komen precies overeen met de spectraallijnen van waterstof. Niels Bohr was hiermee de eerste die de spectraallijnen kon verklaren.

Zowel in de formule als in het diagram zien we dat het elektron in zijn grondtoestand (n = 1) een energie heeft van -13,6 eV. Het elektron ontsnapt dus als het een foton absorbeert van boven de 13,6 eV. In dat geval zeggen we dat het waterstof atoom geïoniseerd is. De ionisatie- of uittree-energie van waterstof is dus gelijk aan 13,6 eV.

Rekenen aan de energieniveaus van het waterstofatoom

Een elektron in een waterstofatoom valt terug van de vierde naar de tweede aangeslagen toestand. Bereken of het foton dat hierbij vrijkomt in het zichtbare deel van het spectrum zit. Het trillen van het waterstofatoom in waterstofjodide kan alleen correct beschreven worden met de kwantummechanica. Het waterstof atoom kan zich in dit molecuul slechts in een paar toestanden bevinden. Hieronder is links het lijnenspectrum te zien van dit molecuul en rechts een afbeelding met daarin de bijbehorende energieniveaus. Teken in het rechter diagram welke overgangen horen bij welk van de spectraallijnen. Licht je antwoord toe. Bepaal de energie van het foton dat vrijkomt als het waterstofatoom van de eerste aangeslagen toestand terugvalt naar de grondtoestand. Druk je antwoord uit in eV. (bron: examen VWO 2016-1) In deze opdracht gaan we de formule voor de energie van het elektron in het waterstofatoom afleiden. Voor het elektron in zijn baan om het proton in het waterstofatoom geldt: $$\frac{fe^2}{r} = mv^2$$ Leid deze formule af met formules uit BINAS. Niels Bohr stelde het elektron in waterstof voor als een golf die rond het proton draait (zie de onderstaande afbeelding). Hij leidde hiermee af dat de snelheid van het elektron in de nde schil gelijk is aan: $$v_n = \frac{n\hbar}{ mr}$$ Er geldt hier dat ℏ gelijk is aan h/(2π). Leid deze formule af. Laat nu zien dat: $$r_n = n^2r_1$$ met: $$r_1 = \frac{\hbar^2}{ fme^2}$$ We gaan nu naar de energie van het elektron in het waterstofatoom kijken. Er geldt: $$E_{tot} = \frac{1}{2}mv^2 - \frac{fe^2}{ r}$$ De tweede term aan de rechter zijde geeft de elektrische energie van het elektron. Laat hiermee zien dat: $$E_n = -\frac{1}{n^2}\left(\frac{fe^2}{2 r_1}\right)$$ Reken de constante tussen haakjes uit en laat hiermee zien dat deze formule geschreven kan worden als: $$E_n = -\frac{13,60 eV}{n^2}$$

§5     Onzekerheid

In eerdere paragrafen hebben we gezien dat deeltjes zowel golf- als deeltjes eigenschappen hebben. In deze paragraaf gaan we dit beter begrijpen met behulp van de onzekerheidsrelatie van Heisenberg.

Als we de schuif meer naar rechts slepen, dan wordt de positie steeds beter te bepalen, maar nu wordt de golflengte onzeker. Een dergelijke golf is namelijk te maken door heel veel sinussen met verschillende golflengtes bij elkaar op te tellen. In de rechter afbeelding zijn de sinussen zichtbaar die hiervoor gebruikt zijn. We hebben hier dus niet te maken met één golflengte, maar met een hele serie.

Bij een deeltje moeten we dus een afweging maken tussen een zekere positie of een zekere golflengte. Beide grootheden kunnen echter niet tegelijk nauwkeurig kenbaar zijn. Omdat de golflengte gerelateerd is aan de impuls via de formule λ = h/p, kunnen we ook zeggen dat we of een zekere positie of een zekere impuls kunnen hebben. Dit idee wordt deonzekerheidsrelatie of ook wel de onbepaaldheidsrelatie van Heisenberg genoemd. Wiskundig wordt dit als volgt beschreven:

$$\Delta x \Delta p \geq \frac{h}{4\pi}$$ Onzekerheid in positie (Δx) meter (m) Onzekerheid in impuls (Δp) kg m/s Constante van Planck (h) 6,62606957 × 10-34 Js

De 'delta's' staan in deze formule voor de onzekerheid. Als een deeltje zich bijvoorbeeld op een onbekende plek in een doosje van lengte L bevindt, dan is de onzekerheid in de plaats gelijk aan L. Als de snelheid van dit deeltje tussen de 20 en 25 m/s ligt, dan is de onzekerheid in de snelheid gelijk aan 25 - 20 = 5 m/s. Met de onzekerheid in de snelheid kan dan als volgt de onzekerheid in de impuls bepaald worden:

Belangrijk is te realiseren dat deze onzekerheid niet ontstaat omdat onze meetinstrumenten niet goed genoeg zijn, maar omdat deeltjes en golven tegenstrijdige kenmerken hebben die niet tegelijk kunnen bestaan. In het dagelijks leven merken we echter weinig van deze onzekerheid, omdat h erg klein is.

Omdat ook geldt dat p = h/λ, kunnen we de onzekerheid in de impuls ook schrijven als: 

Hoewel λ hier onder de deelstreep staat, betekent een grotere onzekere impuls natuurlijk niet een zekere λ. Een onzekere impuls levert natuurlijk ook een onzekere λ.

De onzekerheidsrelatie speelt o.a. een grote rol bij elektronen in atomen. Door de kleine massa van een elektron, is de onzekerheid in de impuls vrij klein en als gevolg is de onzekerheid in de positie relatief groot. Als gevolg is de kansgolf van het elektron vaak in dezelfde orde van grootte als het hele atoom. Als we over elektronen in atomen spreken, spreken we daarom vaak van een elektronenwolk. De atoomkern heeft relatief gezien een veel grotere massa en dus ook een grotere onzekerheid in de impuls. Als gevolg kan de onzekerheid in de positie veel kleiner zijn. De atoomkern heeft dus een veel duidelijker gespecificeerde positie.

We kunnen met de onzekerheidsrelatie ook begrijpen waarom elektronen nooit in de atoomkern vallen, terwijl ze wel elektrisch aangetrokken worden tot de kern. Als het elektron namelijk in de kern zou vallen, dan zou het een veel beter gedefinieerde positie hebben en dus een slecht gedefinieerde snelheid. Met zoveel variatie aan snelheid verspreid het elektron zich weer direct tot een wolk.

Rekenen en redeneren met de onzekerheidsrelatie

We spreken bij atomen vaak over een 'elektronenwolk'. Leg dit uit met behulp van de onzekerheidsrelatie. Leg uit waarom we bij de atoomkern meestal niet over een wolk spreken. Leg aan de hand van de onzekerheidsrelatie uit dat een elektron zich niet in de atoomkern kan bevinden. Leg aan de hand van de onzekerheidsrelatie uit dat een deeltje in een doosje niet stil kan staan. Een elektron beweegt met een snelheid van 300 ± 0,10 m/s door een lege ruimte. Bereken de minimale grootte die de kansgolf van het elektron op dit moment kan hebben. Eerder in dit hoofdstuk hebben we gezien dat een deeltje in een doosje, in bijvoorbeeld zijn grondtoestand, een vaste energie heeft. Voor n = 1 geldt dat: $$E_1 = \frac{h^2}{8mL^2}$$ In eerste instantie lijkt dit niet in overeenstemming met de onzekerheidsrelatie. Leg uit waarom dit zo lijkt. In werkelijkheid moet de onzekerheidsrelatie natuurlijk gelden. De onzekerheid in dit systeem zit verstopt in het feit dat het elektron in het deeltje zowel naar links als naar rechts kan bewegen. Toon aan dat zo toch aan de onzekerheidsrelatie voldaan wordt. Laat hiervoor eerst zien dat: $$p = \frac{h}{2L}$$ En daarna dat: $$\Delta x \Delta p = h$$ Een gepulste laser bestaat niet uit een continue stroom van fotonen, maar uit pakketjes van fotonen. Omdat elk foton zich in een pakketje bevindt, is de onbepaaldheid in de plaats waar hij zich bevindt gelijk aan de lengte van het pakketje. Toon met behulp van de onzekerheidsrelatie aan dat de fotonen in een pakketje niet allemaal dezelfde golflengte kunnen hebben. In de praktijk is het nog niet mogelijk om de lengte van zo'n pakketje fotonen te meten. Wel kan de tijdsduur bepaald worden waarin het foton voorbij een bepaald punt komt. Om die reden gebruikt men in dit soort situaties vaak de zogenaamde tweede Heisenbergrelatie: $$\Delta E \Delta t \geq \frac{h}{4\pi}$$ Leid deze relatie af met behulp van de onzekerheidsrelatie en formules uit BINAS. In de onderstaande grafiek zijn de golflengtes gegeven die in de laserstraal voorkomen bij een pulsduur van 20 femtoseconde. Ga na of de onbepaaldheid van de energie in deze meting overeenkomt met de tweede Heisenbergrelatie. (bron: examen VWO voorbeeldopgaven)

§6     Tunneling

Deeltjes in de kwantumfysica hebben nog een andere merkwaardige eigenschap. Ze kunnen door barrières heen dringen, waar ze volgens de wet van behoud van energie nooit doorheen zouden moeten kunnen komen. Dit proces wordt tunneling genoemd.

Stel dat we in de klassieke natuurkunde een deeltje over een heuvel willen rollen met een bepaalde beginsnelheid. Volgens de mechanica van Newton zal de bal alleen over de heuvel gaan als de kinetische energie gelijk of groter is dan de zwaarte-energie die de bal op de top zal hebben (we verwaarlozen de wrijvingskrachten). Als de kinetische energie niet voldoende is, dan zal de bal weer terugrollen. Deze situatie is linksonder geschetst. In de kwantumfysica bestaat er echter een kleine kans dat het deeltje toch door de barrière heen gaat. Dit is in de rechter afbeelding weergegeven. Dit effect wordt tunneling genoemd. Op macroscopisch niveau zien we tunneling eigenlijk zo goed als nooit gebeuren. Als de grootte van de kansgolf echter in de buurt begint te komen van de grootte van de barrière, dan begint dit effect merkbaar te worden.

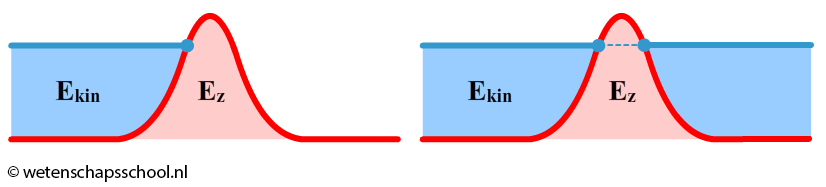
Het effect is te begrijpen met behulp van de onzekerheidsrelatie. Een onzekerheid in de snelheid zorgt voor een onzekerheid in de kinetische energie en deze onzekerheid zorgt ervoor dat tijdelijk even geen rekening gehouden hoeft te worden met behoud van energie - net lang genoeg om toch over de barrière te komen.

De kans op tunnelen hangt af van een aantal factoren. De kans op tunneling neemt toe als:

• de massa van het tunnelende deeltje kleiner wordt
• de barrière dunner wordt (tunneling begint pas merkbaar plaats te vinden als de debroglie-golflengte groter wordt dan de dikte van de barrière)
• de energie van het deeltje groter wordt
• de energie barrière kleiner wordt

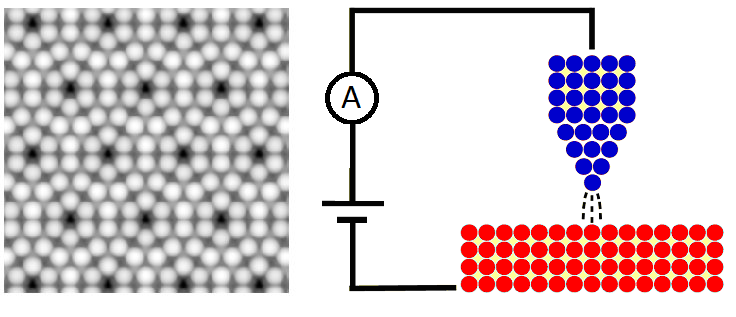
Een ander voorbeeld van een barrière is de elektrische barrière die een elektron ervaart in een atoom door de aantrekkingskracht van de protonen in de kern. Als we een elektron willen laten ontsnappen, dan moet de kinetische energie van dit elektron normaalgesproken groter of gelijk zijn aan de elektrische energie. In de kwantummechanica heeft het elektron echter ook een kleine kans om uit het atoom te tunnelen als er niet voldoende energie is. Hier wordt o.a. gebruik van gemaakt bij de scanning tunneling microscoop (STM). De microscoop bestaat uit een dunne naald die over een aantal atomen beweegt. Hoe dichter de naald bij een atoom komt, hoe kleiner de barrière tussen het elektron en de naald en hoe groter de kans is dat het elektron naar de naald tunnelt. Deze tunnelende elektronen zorgen voor een meetbaar stroompje. Hoe groter deze stroom is, hoe dichter het atoom zich bij de naald bevindt. Door de naald over de atomen te trekken, dan zo een beeld worden gemaakt van de atomen.

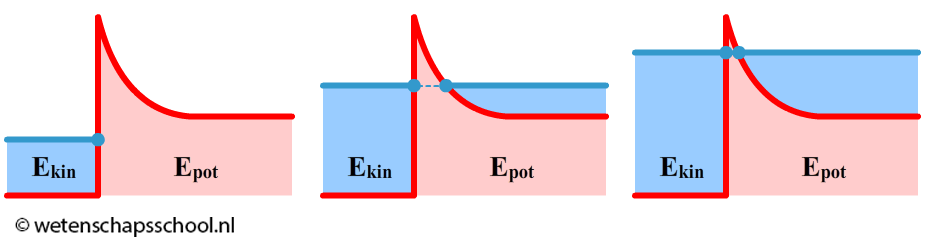
Een ander voorbeeld van tunneling is alfastraling. Bij dit proces tunnelt een heliumkern (twee protonen en twee neutronen) uit een atoomkern. De deeltjes in de kern worden normaalgesproken goed bij elkaar gehouden door de zogenaamde kernkracht. In de kwantummechanica hebben deze deeltjes echter een kans door deze kernkracht-barrière heen te tunnelen. Hieronder zien we het bijbehorende energiediagrammen van dit proces. In de linker afbeelding heeft het deeltje niet genoeg energie om door de barrière heen te kunnen. In het middelste voorbeeld wel. In de rechter voorbeeld gaat het tunnelen nog een stuk gemakkelijker. Niet alleen heeft het deeltje hier meer energie, maar ook de barrière is hier dunner.

Ook bij kernfusie speelt tunneling een grote rol. In het binnenste van de zon worden waterstofatomen gefuseerd tot heliumatomen. De protonen in beide waterstofatomen moeten hiervoor enorm dicht bij elkaar gedrukt worden. Hier is veel kracht voor nodig, omdat protonen elkaar elektrisch afstoten. Volgens de newtoniaanse mechanica zou zelfs in het centrum van de zon de kracht niet groot genoeg zijn om dit voor elkaar te krijgen. Toch kan fusie plaatsvinden, omdat de protonen af en toe wel door tunneling samenkomen. Bij deze fusie komt het zonlicht vrij dat wij dagelijks waarnemen. Zonder tunneling zou de zon dus geen licht geven!

Redeneren met tunneling

Geef in elk van de volgende veranderingen aan of het de tunnelkans vergroot, verkleint of gelijk houdt: De massa van het tunnelde deeltje neemt toe De energiebarièrre wordt dunner De energie van het deeltje wordt groter De energie van de energiebarièrre wordt groter De snelheid waarmee het deeltje tegen de barrière komt wordt groter Het fuseren van waterstof in de zon tot helium zou niet plaatsvinden zonder tunneling. Leg uit waarom fuseren in de Newtoniaanse mechanica niet mogelijk is op de zon. Een deeltje tunnelt van links naar rechts door de onderstaande barrière. Leg uit of de golflengte na het tunnelen groter of kleiner is geworden. Scanning tunneling microscopie (STM) is een techniek waarmee men op atomaire schaal een hoogtekaart van een metaaloppervlak kan maken. Men gebruikt een geleidende, scherpe naald waarvan de punt uit slechts enkele atomen bestaat. Tussen de naald en het metaaloppervlak legt men een kleine spanning aan. Als de naald dicht genoeg bij het oppervlak komt, worden er met het tunneleffect voldoende elektronen uit het metaal 'gezogen' om een stroomsterkte te kunnen meten. Stel de naald beweegt van een plaats tussen twee atomen in, naar een plaats recht boven een atoom. Leg uit wat er dan gebeurt met de afstand tussen het atoom en de naald. Leg ook uit of de tunnelstroom hierdoor toeneemt of afneemt. Onder normale omstandigheden zitten de elektronen opgesloten in het metaal. Ze moeten daarom een energie-barrière ter hoogte van de uittree-energie overwinnen om te ontsnappen. Het tunnelen wordt bevorderd door een kleine spanning tussen de naald en het oppervlak aan te brengen. Geef de reden waarom hierdoor het tunnelen wordt bevorderd. Water kan zich o.a. vormen via de volgende reactie: $$\text{OH} + \text{H}_2 \rightarrow \text{H}_2\text{O} + \text{H}$$ Zoals bij veel reacties moet bij deze reactie een activeringsenergie Ea toegevoegd worden voordat ed reactie op gang komt. Dit is te zien in de onderstaande afbeelding. Deze reactie kan al plaatsvinden bij een temperatuur van 10 K. Bij deze temperatuur kan de reactie echter alleen plaatsvinden door middel van tunelling. Als het H2-deeltje en het OH-deeltje zich voldoende dicht bij elkaar bevinden, dan tunnelt een H-atoom van het H2-deeltje naar het OH-deeltje. Leg uit waarom het water niet net zo snel weer terugtunnelt. Tijdens deze reactie 'verhuist' het H-atoom van het H2-deeltje een afstand a van 1,0 × 10-10 m. Voor deeltjes met een massa m geldt voor de debroglie-golflengte: $$\lambda = \frac{h}{\sqrt{2\pi m k_B T}}$$ kB is hier de constante van Boltzmann. Leg met behulp van deze formule uit of er onder deze omstandigheden een redelijke kans is op het kwantum-tunneleffect. De reactie kan ook worden uitgevoerd als alle waterstofkernen (11H) vervangen worden door deuteriumkernen (21H = D). Dit levert de volgende reactie: $$\text{OD} + \text{D}_2 \rightarrow \text{D}_2\text{O} + \text{D}$$ In beide reacties zijn de hoogte en de breedte van de energiebarrière gelijk, maar toch is hier een andere kans op het kwantum-tunneleffect. Leg uit of deze kans groter of kleiner is. (bron: examen VWO 2018-1) Atoomkernen zwaarder dan lood-208 ondergaan alfaverval. Bij alfaverval breekt een heliumkern vrij van de atoomkern. In de onderstaande afbeelding zien we een vereenvoudigd model van de energiebarrière van de atoomkern. In de linker afbeelding heeft het alfadeeltje 2x zoveel energie als in het rechter geval. In het onderstaande diagram is te zien hoe de energie van de alfadeeltjes afhangt van de halveringstijd. De halveringstijd geeft hier na hoeveel tijd er 50% kans is voor het alfadeeltje om te ontsnappen. Leg uit of de tunnelkans van het linker deeltje veel groter, twee keer zo groot, gelijk, twee keer zo klein of veel kleiner is dan de tunnelkans van het rechter deeltje. Licht je antwoord toe. In werkelijkheid is de energie-barrière niet rechthoekig, maar een dalende functie zoals hieronder is weergegeven: Leg uit dat deze barrière de bovenstaande grafiek beter ondersteunt. Hieronder zien we een alfadeeltje dat uit een Polonium-212 kern tunnelt: Bereken de debrogliegolflengte van het een alfadeeltje als het net ontsnapt is. Gebruik hiervoor BINAS tabel 25. (bron: examen 2016 voorbeeldopgaven)