Hoofdstuk 7
Moment (HAVO)
§1 Het moment
In deze paragraaf gaan we rekenen met krachten werkend op draaiende voorwerpen. We gebruiken hiervoor het begrip moment. Ook gaan we momentevenwichten bestuderen.
In deze paragraaf gaan we het hebben over het principe van de hefboom. Met een hefboom kan je een kleine kracht omzetten in een grote kracht. In de onderstaande afbeelding wordt dit principe gebruikt voor het openen van verfpotten. Zoals je wellicht uit ervaring weet, gaat het openen van een verfpot veel gemakkelijker met een langere schroevendraaier. In de rechter afbeelding geldt hetzelfde principe. Een moer omdraaien met alleen je hand is lastig, maar als je de lengte van een sleutel gebruikt, dan kost dit weinig kracht.

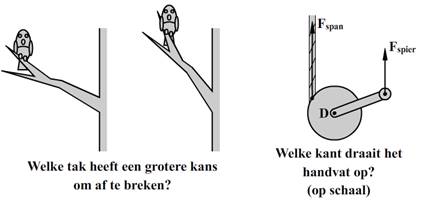
Een hefboom heeft altijd een draaipunt. Dit is duidelijk te zien bij een wip. In de afbeelding linksonder zien we twee personen met gelijke massa die op gelijke afstanden van het draaipunt zitten. De wip is nu in evenwicht. In de rechter afbeelding gaat de linker persoon iets verder van het draaipunt zitten en als gevolg zal de wip aan deze kant dalen. Hoe verder de persoon van het draaipunt gaat zitten, hoe meer invloed de persoon heeft op de draaiing van de wip. We zeggen in zo'n geval dat de persoon dan een groter moment uitoefent op de wip.

We kunnen het moment als volgt berekenen:
|
… $$ M = F \times r $$
|
De arm (r) is de afstand van het draaipunt tot de kracht die op het voorwerp werkt. Later in deze paragraaf gaan we nog een iets preciezere definitie van de arm tegenkomen.
Als een voorwerp in evenwicht is, dan is de som van de momenten die het voorwerp linksom pogen te draaien gelijk aan de som van de momenten die het voorwerp rechtsom pogen te draaien. In formuletaal wordt dit:
|
… $$ \Sigma M_{L} = \Sigma M_{R} \;\;\;\; \text{(evenwicht)}$$
|
Een bekend voorbeeld waar momenten een belangrijke rol spelen is de hijskraan. Deze gigantische kranen kunnen zware voorwerpen optillen zonder om te vallen. Dit kan omdat de kraan in evenwicht wordt gehouden door een contragewicht (zie de onderstaande afbeelding). Door de positie van dit contragewicht te verplaatsen, en dus de arm te veranderen, wordt de kraan in evenwicht gehouden.

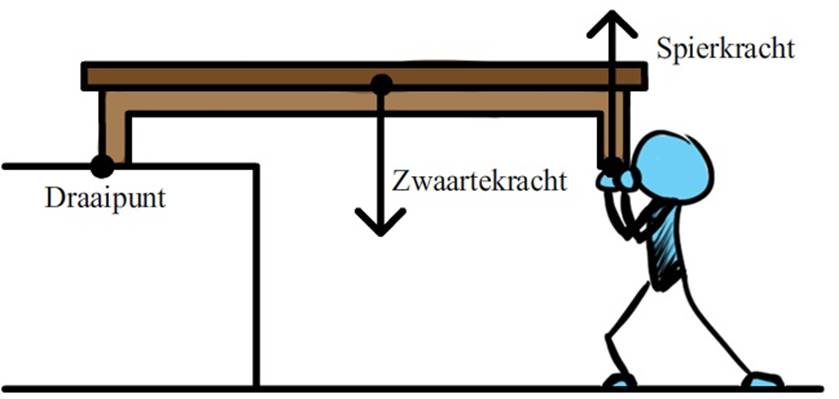
Nog een voorbeeld. In de volgende afbeelding tilt een persoon een bank op die op een verhoging ligt. De bank is 4,0 m lang en heeft een massa van 10 kg. Het zwaartepunt van de bank bevindt zich in het midden van de bank en daar tekenen we dus de zwaartekracht. De arm van de zwaartekracht is de afstand van het draaipunt tot de zwaartekracht. Omdat de zwaartekracht in het midden van de bank werkt, is de bijbehorende arm dus 2,0 m lang. De arm van de spierkracht is 4,0 m. Er geldt dus:
$$ F_z \times r_z = F_{spier} \times r_{spier} $$
$$ 10 \times 9,81 \times 2 = F_{spier} \times 4 $$
$$ F_{spier} = 49 \text{ N} $$
|
|
|
1. Maak het stencil op de volgende bladzijde.
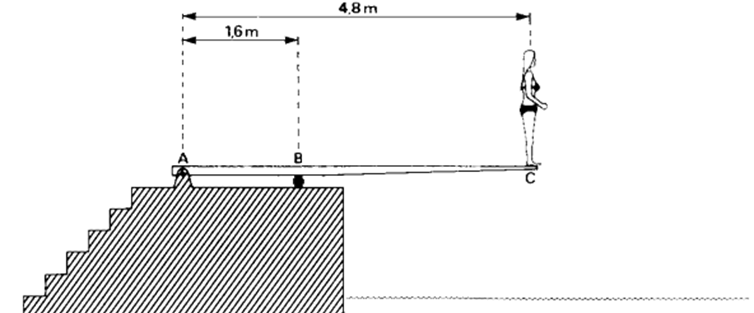
2. Een meisje met een massa van 45 kg staat op het uiteinde C van een duikplank. De duikplank kan draaien om as A en ligt in B op een steunpunt. De massa van de plank wordt in dit vraagstuk verwaarloosd. De afstand tussen as A en steunpunt B is 1,6 m; de afstand tussen as A en uiteinde C is 4,8 m.
a. Bereken de grootte van de kracht die door het steunpunt B op de plank wordt uitgeoefend als het meisje in C op de duikplank staat. b. Op punt A werkt ook een kracht. Leg uit waarom het niet nodig was rekening te houden met deze kracht in opdracht a. c.
Bereken de grootte van deze kracht werkende op punt
A als het meisje stilstaat op de duikplank. |
Stencil momenten
Momenten Deel I: horizontale armen
§2 De arm
In deze paragraaf gaan we het begrip arm iets nauwkeuriger definiëren. We zijn hiermee in staat complexere met complexere momentevenwichten te rekenen.
Nu is het tijd voor de iets nauwkeurigere definitie van de arm. Hieronder zien we links een kracht en het bijbehorende draaipunt. Om de arm te vinden tekenen we de lijn van de kracht eerst door in beide richtingen. We noemen dit de werklijn van de kracht. De arm voldoet dan aan de volgende twee eisen:
· De arm loopt van het draaipunt tot aan de werklijn van de kracht.
· De arm staat loodrecht op de werklijn van de kracht.

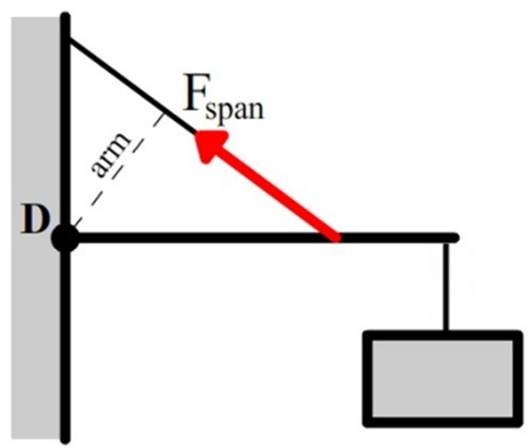
We hebben deze definitie hieronder toegepast. We zien hier een uithangbord dat omhoog gehouden wordt met een touw. De arm van de spankracht in het touw loopt hier van het draaipunt tot de werklijn van de kracht en staat inderdaad loodrecht op de werklijn. Deze arm voldoet dus aan de bovenstaande definitie.
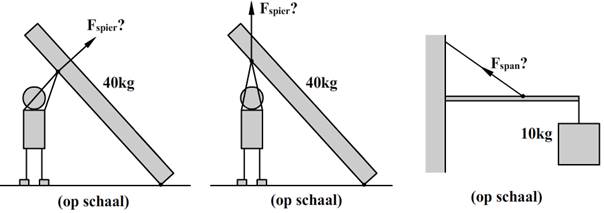
Nog een voorbeeld. In de linker onderstaande afbeelding zien we een persoon die een bank met een massa van 15 kg optilt. In de afbeelding is ook de spierkracht weergegeven die de persoon uitoefent. Stel we willen de grootte van deze spierkracht bepalen. Hoe doen we dat?
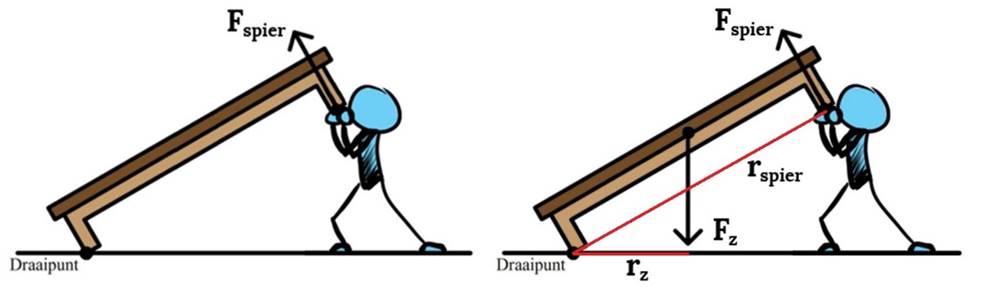
Het aangrijppunt van de zwaartekracht is het midden van de bank. In de rechter bovenstaande afbeelding zijn van zowel de zwaartekracht als de spierkracht de armen getekend. Wederom lopen deze armen van het draaipunt naar de werklijn van de kracht en staan ze loodrecht op deze kracht.
De grootte van de spierkracht bepalen we als volgt:
…
$$ M_{spier} = M_{z} $$
…
…
$$ F_{spier} \times r_{spier} = F_{z} \times r_z $$
…
Nu meten we de armen op:
$$ F_{spier} \times 4,8 = 15 \times 9,81 \times 1,9 $$
…
$$ F_{spier} = 4,6 \times 10^2 \text{ N} $$
|
|
|
1. Maak het stencil op de volgende bladzijde.
2. Beschrijf hoe je de arm van een kracht kan vinden.
3.
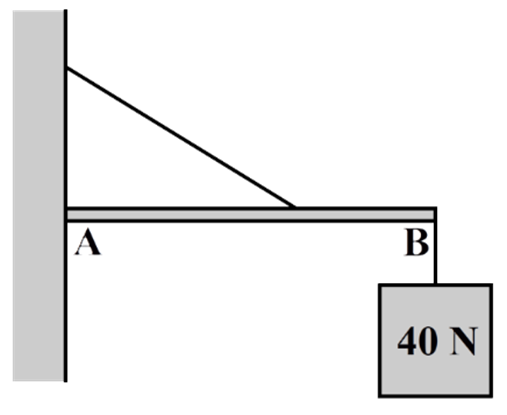
Een uithangbord is aan een staaf
AB opgehangen. De zwaartekracht werkend op het bord is 40 N. De zwaartekracht
werkende op de staaf mag je verwaarlozen. De staaf wordt op zijn plek
gehouden met behulp van een touw. Bereken de spankracht in het touw.
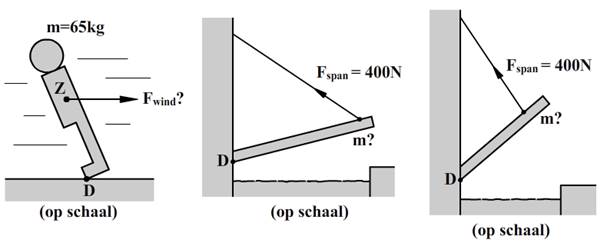
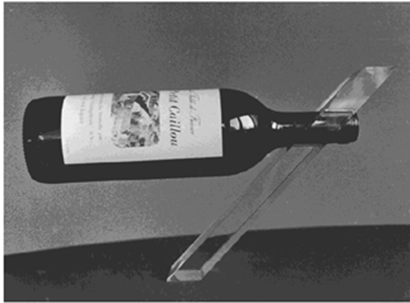
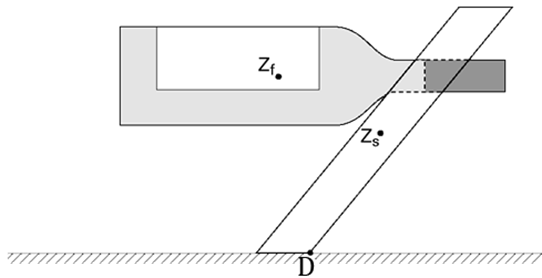
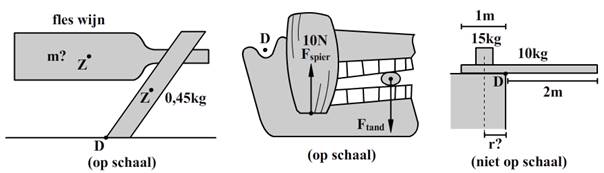
4. In cadeauwinkels tref je de onderstaande flessenstandaard aan. Het is een stuk perspex met een gat waarin de hals van een fles geschoven kan worden. Het stuk perspex kan met de fles in evenwicht worden neergezet. Het is dan niet nodig het perspex aan de ondergrond vast te maken. a. Arceer het gebied in de foto waarin het zwaartepunt van het geheel zich moet bevinden opdat er evenwicht is. b.
De fles wordt nu zo ver in het gat geschoven dat de
standaard op het punt staat naar rechts te kantelen. Bepaal met behulp van de
onderstaande figuur de massa van de fles wijn. Ga ervan uit dat de figuur op
schaal is weergegeven en dat de massa van de standaard gelijk is aan 0,45 kg.
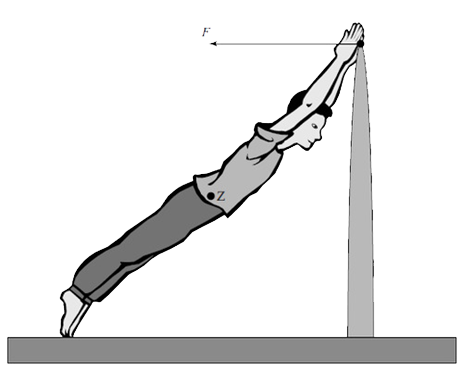
c. (bron: examen VWO 2000-1) 5. Bij de turnoefening duwt een persoon tegen een steunbalk (zie de onderstaande afbeelding). De balk oefent dan alleen een horizontaal gerichte kracht uit op de persoon. De massa van de persoon is 75 kg. … Bepaal aan de hand van de afbeelding de grootte van
de horizontale kracht van de steunbalk op de persoon.
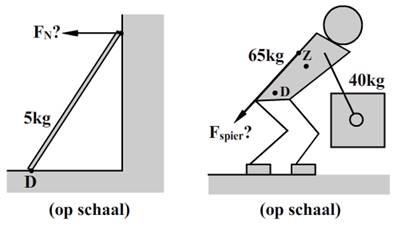
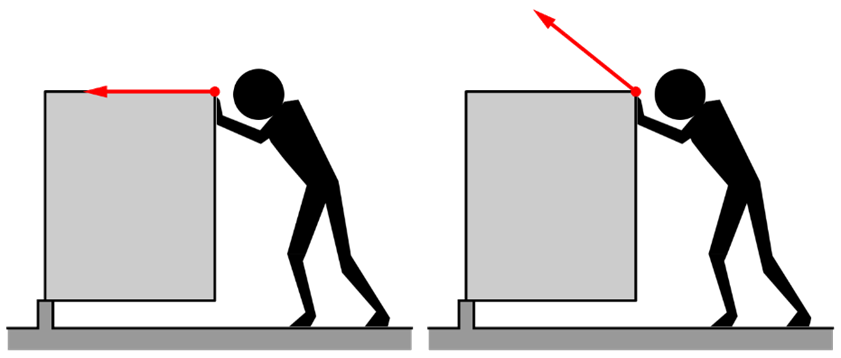
6.
Een persoon wilt zo gemakkelijk
mogelijk een groot blok in evenwicht houden op dat aan één zijde op een
steunpunt leunt. In de onderstaande afbeelding zien we de persoon in twee
richtingen duwen tegen het blok. Het blok is niet op schaal weergegeven. a. Leg met behulp van de bovenstaande afbeelding uit in welke richting de persoon minder kracht uit hoeft te oefenen om het blok in evenwicht te houden. b. Het blok heeft een massa van 150 kg, een breedte van het blok is 50 cm en de hoogte is 120 cm. Bereken met deze gegevens spierkracht van de persoon in beide gevallen.
|
Stencil momenten
Momenten Deel II: Algemeen