In deze paragraaf gaan we leren hoe druk in water werkt. Laten we beginnen met een experiment dat hieronder is weergegeven. In een bak water zijn twee gaten gemaakt op verschillende hoogten. Zoals je ziet schiet het water met een hogere snelheid uit het onderste gat. Er werkt hier blijkbaar een grotere druk dan bij het bovenste gat. Hoe dieper we ons dus in het water bevinden, hoe hoger de druk.

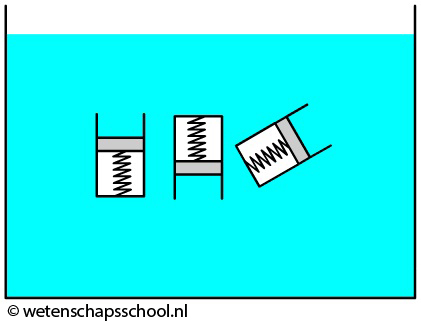
Een simpele manier een druk te meten in water is met behulp van een veer waarvan de veerconstante nauwkeurig bepaald is. Je zal dan merken dat hoe dieper dit meetapparaat zich in het water bevindt, hoe meer de veer in zal drukken. Het zal je wellicht verbazen dat de druk die je meet niet afhangt van de oriëntatie van het meetinstrument. De druk blijkt dus gelijk te zijn in alle richtingen (zie de onderstaande afbeelding).
In de onderstaande afbeelding zien we een bak met water. We bestuderen de krachten die werken op het deel van het water dat zich binnen de stippellijnen bevindt. Aan de bovenkant werkt hier de luchtdruk die het water naar beneden duwt. Aan de onderkant werkt een druk omhoog van het water. Er werken ook krachten aan de linker en rechter wand, maar deze heffen elkaar op. Als laatste werkt er ook nog een zwaartekracht op het water.
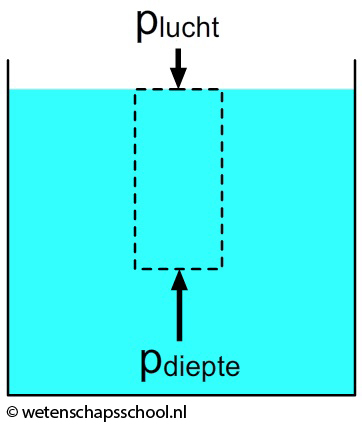
Omdat het water stilstaat moeten de krachten in evenwicht zijn. Er geldt dus:
$$ F_{diepte} = F_{lucht} + F_z $$Met de formule p = F/A kunnen we de kracht die de lucht op dit water uitoefent schrijven als Flucht = plucht × A. We kunnen de bovenstaande formule daarom schrijven als:
$$ p_{diepte} A = p_{lucht} A + mg $$Als we beide kanten delen door A en de formule voor de dichtheid invullen voor m, dan vinden we:
$$ p_{diepte} = p_{lucht} + \frac{\rho_{water} Vg}{A} $$Omdat V / A gelijk is aan de diepte van het water (d), vinden we:
| Druk op diepte d (pdiepte) | Pascal (Pa) |
| Luchtdruk (plucht) | Pascal (Pa) |
| Dichtheid (ρ) | kilogram per kubieke meter (m3) |
| Diepte (d) | meter (m) |
Laten we als voorbeeld een berekening doen aan een onderzeeboot die zich op een diepte van 300 meter bevindt. Voor de dichtheid gebruiken we 1,03 × 103 kg/m3, de dichtheid van zeewater. De formule wordt:
$$ p = 1,0 \times 10^5 + 1,03 \times 10^3 \times 9,81 \times 300 = 3,1 \times 10^6 \text{ Pa} $$Als we dit vergelijken met de luchtdruk, dan vinden we:
$$ \frac{3,1 \times 10^6}{1,0 \times 10^5} = 31\times $$De druk is hier dus 31x zo sterk als de luchtdruk! Dit betekent dat als je bijvoorbeeld een raam wilt bouwen in een onderzeeboot, dat je deze heel sterk moet maken om deze druk te kunnen weerstaan.
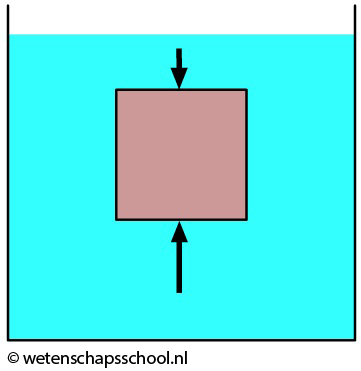
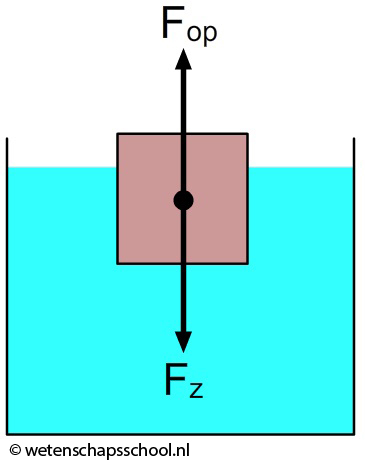
In de onderstaande afbeelding zien we een blok dat zich onder water bevindt. Omdat de onderkant van het blok zich dieper in het water bevindt, heerst hier een grotere druk dan boven aan het blok. Dit betekent dat de druk netto zorgt voor een kracht omhoog. We noemen dit de opwaartse kracht. We merken deze kracht bijvoorbeeld als we een opblaasbal onder water proberen te duwen. De opwaartse kracht levert hier een behoorlijke tegenwerking.
In de onderstaande linker afbeelding zien we links weer water dat zich bevindt binnen een stippellijn. Als het water stilstaat (en daar gaan we hier vanuit), dan moeten de krachten volgens de eerste wet van Newton op dit water in evenwicht zijn. De opwaartse kracht op dit water en de zwaartekracht op dit water moeten dus gelijk zijn:
$$ F_{op} = F_{z,water} $$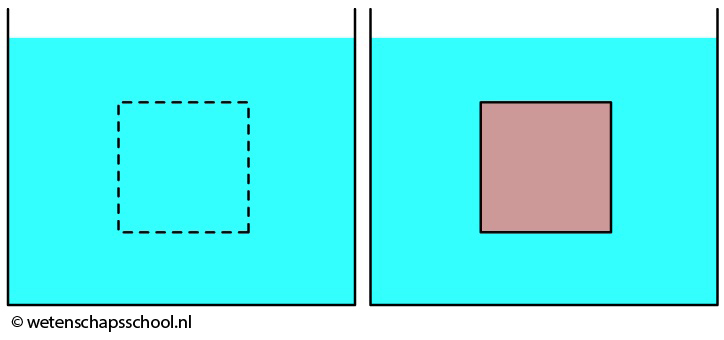
Stel dat we het water binnen de stippellijnen konden verwijderen en in plaats daarvan een voorwerp plaatsen van dezelfde grote (zie de rechter bovenstaande afbeelding). Aangezien het water buiten de stippellijn onveranderd is gebleven, oefent dit water dezelfde druk uit op dit voorwerp als dat het deed op het water binnen de stippellijn. Ook hier moet dus gelden dat de opwaartse kracht gelijk is zwaartekracht van het water (!) dat zich eerst op de plek van het blok bevond. We noemen dit het verplaatste water. Er geldt dus:
$$ F_{op} = F_{z,water} $$Dit kunnen we uitschrijven tot:
$$ F_{op} = m_{water} g $$Dit kunnen we uitschrijven tot de zogenaamde wet van Archimedes:
| De opwaartse kracht (Fop) | newton (N) |
| Dichtheid (ρ) | kilogram per kubieke meter (m3) |
| Volume van het verplaatste water (V) | kubieke meter (m3) |
| Valversnelling (g) | 9,81 m/s2 |
Of het blok dat we onder water hebben geplaatst zal drijven of zinken hangt af van de grote van de opwaartse kracht en de zwaartekracht van het blok zelf. Voor deze zwaartekracht geldt:
$$ F_{z,blok} = m_{blok}g = \rho_{blok} V_{blok} g $$Er geldt dus:
$$ F_{z,blok} \lt F_{op} \;\;\;\; \text{ (drijven)} $$ $$ F_{z,blok} \gt F_{op} \;\;\;\; \text{ (zinken)} $$Oftewel:
$$ \rho_{blok} V_{blok} g \lt \rho_{water} V_{water} g \;\;\;\; \text{ (drijven)} $$ $$ \rho_{blok} V_{blok} g \gt \rho_{water} V_{water} g \;\;\;\; \text{ (zinken)} $$En dit kunnen we versimpelen tot:
$$ \rho_{blok} V_{blok} \lt \rho_{water} V_{water} \;\;\;\; \text{ (drijven)} $$ $$ \rho_{blok} V_{blok} \gt \rho_{water} V_{water} \;\;\;\; \text{ (zinken)} $$Als het blok zich helemaal onder water bevindt, dan zijn Vwater en Vblok aan elkaar gelijk. Het water binnen de stippellijn en het blok zelf hebben dan immers dezelfde grootte. In dat geval hangt het verschil tussen zinken en drijven dus alleen nog af van de dichtheid:
En dit is precies de regel die we in hoofstuk 1 hebben geleerd in de paragraaf 'drijven en zinken'.
Als laatste bestuderen we een voorwerp dat drijft (zie de onderstaande afbeelding). Een deel van dit voorwerp steekt boven het water uit en een deel bevindt zich onder water.
Als het voorwerp stil ligt, dan kunnen we er weer vanuit gaan dat de krachten in evenwicht moeten zijn. De zwaartekracht en de opwaartse kracht moeten dus ook hier in evenwicht zijn:
$$ F_{op} = F_{z,blok} $$Als we dit uitwerken, dan vinden we:
$$ \rho_{water} V_{water} g = \rho_{blok} V_{blok} g $$Dit kunnen we versimpelen tot:
$$ \rho_{water} V_{water} = \rho_{blok} V_{blok} $$Dit kunnen we omschrijven tot:
| Volume van het verplaatste water (Vwater) | kubieke meter (m3) |
| Dichtheid van het blok (ρblok) | kilogram per kubieke meter (m3) |
| Dichtheid van het water (ρwater) | kilogram per kubieke meter (m3) |
| Volume van het het blok (Vblok) | kubieke meter (m3) |
Met deze formule kunnen we uitrekenen hoeveel procent van het voorwerp onder water zal liggen. Neem bijvoorbeeld een ijsberg. Met dit dichtheid voor ijs en zeewater vinden we:
$$ V_{water} = \frac{917}{1030} V_{ijsberg} $$ $$ V_{water} = 0,89 \times V_{ijsberg} $$We zien hier dat slechts 89% van het volume van de ijsberg zich in het water bevindt. Een ijsberg bevindt zich dus voor het overgrote deel onder water (zie de onderstaande afbeelding).
