De theorie van Bohr kon het waterstof veel beter beschrijven dan de theorie van Newton, maar na verloop van tijd werd toch gevonden dat de theorie niet helemaal overeenkwam met de realiteit. Daarnaast werkte de methode helemaal niet bij atomen complexer dan waterstof. De theorie van Bohr was dus een goede eerste stap, maar nog niet het hele verhaal.

De volgende stap was de zogenaamde Schrödingervergelijking. Een algemene golfvergelijking waarmee we de beweging van kwantumgolven kunnen beschrijven. We gebruiken voor de kwantumgolf het symbool Ψ. We noemen dit ook wel de golffunctie.

In deze paragraaf zullen we laten zien hoe we deze formule kunnen vinden op basis van deze eerder gevonden eigenschappen van de kwantumgolf:

$$ p = h/\lambda $$ $$ E = hf $$

Om formules in de rest van het hoofdstuk iets te versimpelen, gaan we deze formules iets anders schrijven met behulp van ℏ=h/(2π), k = 2π/λ en ω = 2πf. We vinden hiermee:

$$ p = \hbar k $$ $$ E = \hbar\omega $$

In de Newtoniaanse mechanica heeft elk deeltje kinetische en potentiële energie. Er geldt dus:

$$ E = E_{kin} + E_{pot} $$ $$ E = \frac{p^2}{2m} + E_{pot} $$

Als we in deze formule de kwantummechanische formules \(p = \hbar k \) en \(E = \hbar\omega\) invullen, dan vinden we de kwantummechanische formule voor de energie:

$$ \frac{\hbar^2k^2}{2m} + E_{pot} = \hbar\omega $$

Om zijn golfvergelijking te vinden, koos Schrödinger een simpel sinusvormig golfje om zijn vergelijkingen mee te testen. De algemene formule voor een stilstaande sinusvormige golf met golflengte λ wordt gegeven door:

$$ \Psi = \sin{ \left( \frac{2\pi x}{\lambda} \right)} $$

Als we ook nog willen dat dit golfje naar rechts gaat bewegen, dan vervangen we 'x' door 'x - vt'. Als de tijd t nu toeneemt, dan start de sinus een steeds grotere x. We vinden dan:

$$ \Psi = \sin{ \left( \frac{2\pi}{\lambda} (x - vt)\right)} $$

Met v = fλ kunnen we dit herschrijven tot:

$$ \Psi = \sin{ \left( \frac{2\pi x}{\lambda} - 2\pi ft \right)} $$

Met k = 2π/λ en ω = 2πf versimpelt dit tot:

$$ \Psi = \sin{ (kx - \omega t)} $$

Schrödinger ging toen op zoek naar een golfvergelijking die met het bovenstaande golfje de kwantummechanische energie van het deeltje zou teruggeven. Zijn eerste gok was:

$$ - \frac{\hbar^2}{2m} \frac{\partial^2 \Psi}{\partial x^2} + E_{pot}\Psi = \hbar \frac{\partial \Psi}{\partial t} $$

Als we het testgolfje namelijk in deze vergelijking stoppen, dan levert de tweede afgeleide naar de plaats aan de linkerkant een extra factor k² en de eerste afgeleide naar de tijd aan de linkerkant een extra factor ω. Deze factoren komen ook voor in onze energievergelijking. We vinden:

$$ -\frac{\hbar^2k^2}{2m} \sin{(kx - \omega t)}+ \sin{(kx - \omega t)}E_{pot} = -\hbar \omega\cos{(kx - \omega t)} $$

Deze vergelijking lijkt lichtelijk op de energievergelijking, maar probleem is dat we de cosinus en sinussen niet kunnen wegstrepen. We komen dus niet op de kwantummechanische energievergelijking uit zoals Schrödinger gehoopt had. Dit pad liep dus dood.

Omdat de sinus in de golffunctie niet werkte, gebruikte Schrödinger een e-macht. De afgeleide van e^x naar is is namelijk wederom e^x en als deze e-machten onverandert blijven, kunnen we ze na het differentiëren wel wegstrepen. Een golf die hieraan voldoet is:

$$ \Psi = e^{i(kx-\omega t)} $$

Om te begrijpen wat we hier zien is het handig eerst een voorstelling te maken van e^ix. Deze formule beschrijft een spiraal met straal 1 in de imaginaire ruimte (zie de onderstaande afbeelding). Door de extra term '-ωt' in de macht gaat beweegt deze spiraal ook nog eens langs de x-as vooruit.

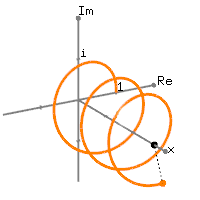
De Schrödingervergelijking die hier het juiste resultaat levert is:

$$ - \frac{\hbar^2}{2m} \frac{\partial^2\Psi}{\partial x^2} + E_{pot}\Psi = i\hbar \frac{\partial \Psi}{\partial t} $$

Als we de golffunctie invullen, dan vinden we:

$$ \frac{\hbar^2k^2}{2m} e^{i(kx-\omega t)} + E_{pot} e^{i(kx-\omega t)} = \hbar \omega e^{i(kx-\omega t)} $$

Na het wegstrepen van de e-macht, vinden we:

$$ \frac{\hbar^2k^2}{2m} + E_{pot} = \hbar \omega $$

Dit is de correcte energievergelijking. De Schrodingervergelijking wordt dus:

$$ - \frac{\hbar^2}{2m} \frac{\partial^2\Psi}{\partial x^2} + E_{pot}\Psi = i\hbar \frac{\partial \Psi}{\partial t} $$

Dit komt allemaal mooi uit, maar we hebben hier wel iets heel vreemds moeten aannemen. Onze kwantumgolfjes roteren in de imaginaire ruimte! Hoe vreemd dit ook klinkt, zullen we verder in dit hoofdstuk zien dat we met deze vergelijking het hele periodieke systeem kunnen afleiden.