De Newtoniaanse mechanica is gebasseerd op de wetten van Newton. In de 19de eeuw ontdekte de briljante wetenschappers Euler, Lagrange en een aantal tijdgenoten dat deze zelfde mechanica ook met een andere basis beschreven kon worden. Deze versie wordt de Lagrangiaanse mechanica genoemd. Deze versie van de mechanica had een aantal voordelen en is het onderwerp van de volgende paragraaf. In deze paragraaf gaan we de wiskunde behandelen die we hiervoor nodig hebben - de zogenaamde variatiecalculus.

De eerste persoon die bezig was met een simpele vorm van variatiecalculus was Fermat. Fermat ontdekte dat als hij een lichtstraal vanaf een willekeurig punt S naar een andere willekeurig punt D wilde schijnen, dat het licht dan altijd het pad nam dat het minste tijd kost. Dit wordt het principe van Fermat genoemd. Dit principe geldt zelfs als punt S zich bijvoorbeeld in de lucht bevindt en punt D onder water. In de onderstaande afbeelding legt het licht tussen punt S en D altijd pad SLD af. Dit pad kost de minste tijd omdat licht sneller voortbeweegt in lucht dan in water. Het scheelt op deze manier een beetje tijd als het licht net iets langer in de lucht blijft bewegen.

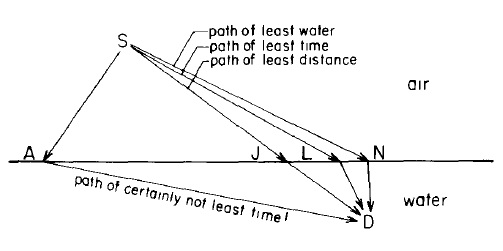
In de tijd van Fermat was het een compleet mysterie waarom licht dit deed. Het leek of het licht van tevoren alle mogelijke paden bestudeerde en dan het pad koos waar de tijdduur het kortst was. Het begrijpen van dit mysterie kwam pas in de 20^ste eeuw met de kwantummechanica (hierover later meer).

Omdat licht dus altijd het pad kiest waar de tijd minimaal is, werd het handig om een wiskunde te ontwikkelen waarbij een pad bepaald kon worden waarbij een bepaalde waarde (zoals de tijd) minimaal is. Deze wiskunde wordt de variatiecalculus genoemd.

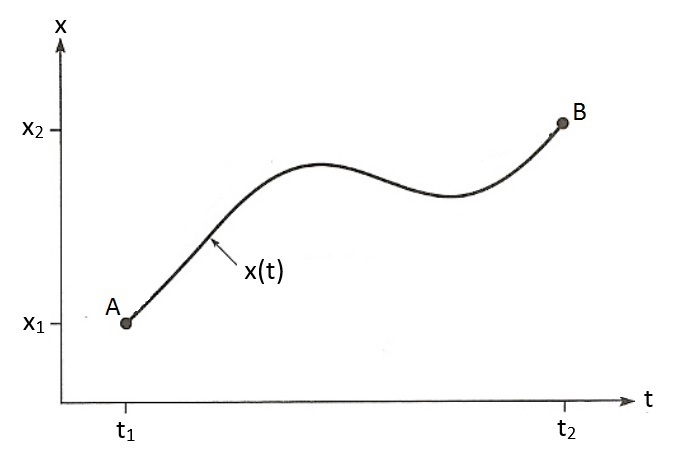
Stel dat een deeltje onder invloed van een aantal krachten beweegt van punt A naar punt B en dat het het pad van het deeltje gegeven wordt door de functie x(t). De beweging start op tijdstip t₁ en eindigt op tijdstip t₂ (zie de onderstaande afbeelding).

De waarde die we minimaal willen maken noemen we de actie S. In het geval van het principe van Fermat zouden we de S gelijk stellen aan de tijd. We gaan hier echter iets algemener te werk. Het blijkt dat de variatiecalculus werkt voor alle S waarvoor de volgende formule geldt:

$$ S = \int^{t_2}_{t_1} L(x,\dot{x}) dt \;\;\;\; \text{(minimaal)}$$

S is hier gelijk aan de integraal over de tijd van een willekeurige functie L die afhankelijk is van x en zijn afgeleide naar de tijd. Als we L gelijkstellen aan 1, dan wordt de integraal gelijk aan de tijd en dan is S gelijk aan t, zoals bij het principe van Fermat, maar hetzelfde principe dat we hier gaan uitwerken geldt dus ook voor heel veel andere uitdrukkingen voor L.

Als S minimaal is, dan betekent dat dat alle nabijgelegen paden \(\tilde{x}\) een grotere waarde voor S moeten hebben.

$$ S = \int^{t_2}_{t_1} L(\tilde{x},\dot{\tilde{x}}) dt \;\;\;\; \text{(niet minimaal)}$$

Een nabijgelegen pad definiëren we als volgt:

$$ \tilde{x} = x + \alpha \eta(t) $$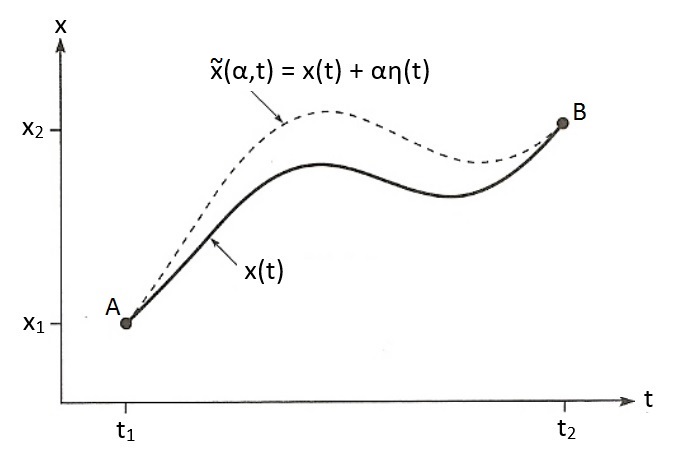

η(t) is een willekeurige functie die als eigenschap heeft dat deze nul is op tijdstip t₁ en t₂, zodat alle paden wel beginnen in punt A en eindigen in punt B. Er geldt dus:

$$ \eta(t_1) = \eta(t_2) = 0 $$

α is hier een constante die we kunnen invullen zoals we willen. Als we α = 0 kiezen, dan krijgen we het oorspronkelijke pad x(t) terug waarbij S minimaal is. Bij een andere α wordt S groter dan het minimum. Als we dus een grafiek zouden maken van de waarde van S bij verschillende α, dan vinden we:

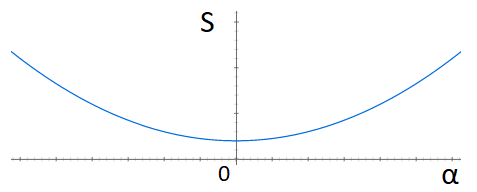
Omdat de grafiek bij α=0 horizontaal loopt, is de helling op dat punt nul. Er geldt dan dus:

$$ \frac{dS}{d\alpha} = 0 \;\;\;\; (\text{als }\alpha = 0)$$

Met de definitie van S kunnen we dit uitschrijven tot:

$$ \frac{d }{d\alpha} \int^{t_2}_{t_1} L dt = 0 $$

Met de Leibniz-regel kunnen we dit omschrijven tot:

$$ \int^{t_2}_{t_1} \frac{\partial L }{\partial \alpha} dt = 0 $$

De afgeleide van L naar α kunnen we met de zogenaamde kettingregel als volgt uitschrijven:

$$ \int^{t_2}_{t_1} \left( \frac{\partial L }{\partial \tilde{x}} \frac{\partial \tilde{x} }{\partial \alpha} + \frac{\partial L }{\partial \dot{\tilde{x}}} \frac{\partial \dot{\tilde{x}} }{\partial \alpha} \right)dt = 0 $$

Met behulp van \( \tilde{x} = x + \alpha \eta \) vinden we:

$$ \frac{\partial \tilde{x} }{\partial \alpha} = \eta $$ $$ \frac{\partial \dot{\tilde{x}} }{\partial \alpha} = \dot{\eta} $$

Als we deze uitspraken in de bovenstaande uitspraak stoppen, dan vinden we:

$$ \int^{t_2}_{t_1} \left( \frac{\partial L }{\partial \tilde{x}} \eta + \frac{\partial L }{\partial \dot{\tilde{x}}} \dot{\eta} \right)dt = 0 $$

Met behulp van partiële integratie kunnen we de tweede term in de integraal herschrijven:

$$ \frac{\partial L }{\partial \dot{\tilde{x}}}\eta(t_2) - \frac{\partial L }{\partial \dot{\tilde{x}}}\eta(t_1) - \int^{t_2}_{t_1} \left( \frac{\partial L }{\partial \tilde{x}} \eta - \frac{d}{dt}\frac{\partial L }{\partial \dot{\tilde{x}}} \eta \right) dt = 0 $$

Omdat η(t₁) = η(t₂) = 0, vallen de eerste twee termen weg. We houden dus over dat:

$$ \int^{t_2}_{t_1} \left( \frac{\partial L }{\partial \tilde{x}} \eta - \frac{d}{dt}\frac{\partial L }{\partial \dot{\tilde{x}}} \eta \right) dt = 0 $$

Als we nu η buiten haakjes halen, dan vinden we:

$$ \int^{t_2}_{t_1} \left( \frac{\partial L }{\partial \tilde{x}} - \frac{d}{dt}\frac{\partial L }{\partial \dot{\tilde{x}}} \right) \eta dt = 0 $$

Om deze integraal daadwerkelijk nul te maken, moet of het deel tussen de haken of η(t) gelijk zijn aan nul. η(x) is echter een willekeurige functie, die we zelf kunnen kiezen en is dus niet noodzakelijk gelijk aan nul. De term tussen haakjes moet dus nul worden. Er geldt dus:

$$ \frac{\partial L }{\partial \tilde{x}} - \frac{d}{dt}\frac{\partial L }{\partial \dot{\tilde{x}}} = 0$$

Bij α = 0 wordt dit:

$$ \frac{\partial L }{\partial x} - \frac{d}{dt}\frac{\partial L }{\partial \dot{x}} = 0$$

Dit wordt de Euler-Lagrange vergelijking genoemd. Deze vergelijking vertelt ons dat L een minimale S oplevert als aan deze vergelijking voldaan wordt.