Nog voordat Newton zijn mechanica had bedacht, had Johannes Kepler een aantal patronen ontdekt in de beweging van de planeten in hun baan om de zon. We noemen dit de wetten van Kepler:
- Planeten bewegen in ellipsbanen om de zon. De zon bevindt zich in een focuspunt van de ellips.
- De oppervlakte die de radiusvector in geljike tijdsintervallen overbrugt is constant.
- Voor de omlooptijd (T) en de langste straal van de ellips (a) geldt T2/a3=constant.
Kepler had deze patronen geobserveerd, maar niemand in zijn tijd kon deze wetten verklaren. Het was uiteindelijk Newton die met zijn mechanica liet zien waar deze drie wetten vandaan kwamen. Zijn bewijs van deze drie wetten gaven overweldigend bewijs dat de gravitatie-theorie van Newton correct was en dit maakte Newton één van de belangrijkste denkers uit de wereldgeschiedenis. In deze paragraaf volgen de Newton's voetstappen door deze wetten af te leiden.
De tweede wet van Kepler
We beginnen met de tweede wet. We beginnen bij de onderstaande afbeelding. We zien hier een planeet die een afstand AB afgelegd in tijdsduur Δt.
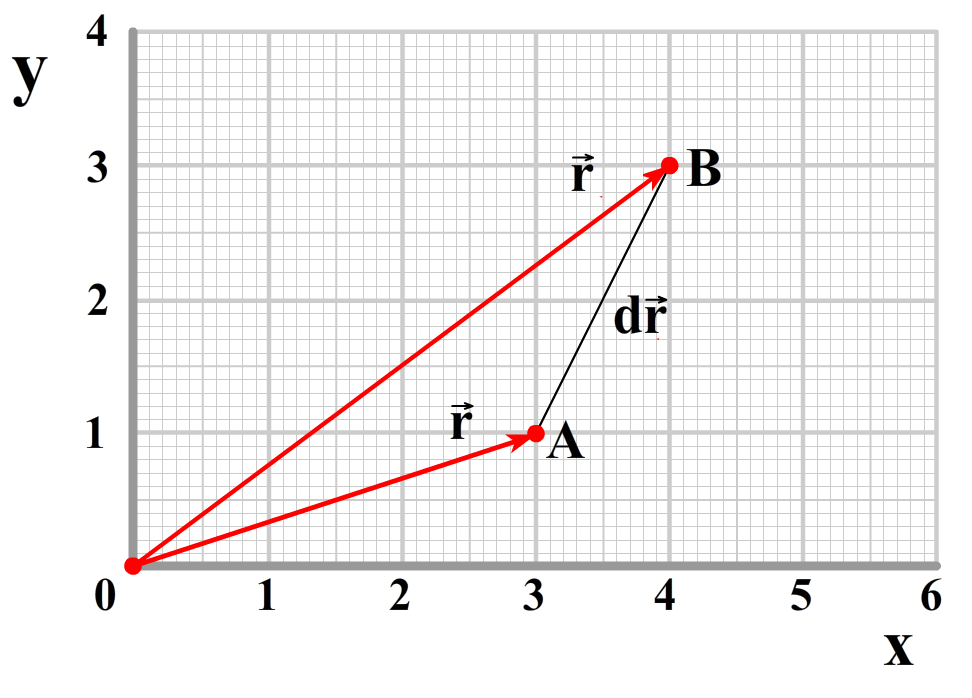
We willen nu het oppervlak A van deze driehoek te weten komen. Het oppervlak van een willekeurige driehoek kunnen we met de onderstaande afbeelding vinden. Zoals je weet is het oppervlak gelijk aan 1/2(b × h). Omdat ook geldt dat sin(θ)=h/a, kunnen we dit combineren tot:
$$ dA = \frac{1}{2} b a \sin{\theta} = \frac{1}{2} \vec{a} \times \vec{b} $$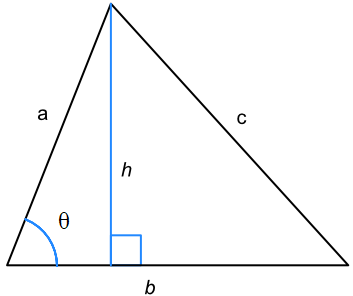
Als we dit toepassen op de driehoek van de beweging van de planeet, dan vinden we:
$$ dA = \frac{1}{2} \vec{r} \times \vec{dr} $$De willen weten hoe dit oppervlak verandert in de tijd. We gaan dus de afgeleide in de tijd nemen:
$$ \frac{dA}{dt} = \frac{1}{2} \vec{r} \times \vec{v} $$Vergelijk de rechter term nu eens met de formule voor het impulsmoment:
$$ L = m(\vec{r} \times \vec{v}) $$Als we dit invullen in onze formule voor dA/dt, dan vinden we:
$$ \frac{dA}{dt} = \frac{L}{2m} $$Omdat L en m constant zijn, hebben we hiermee bewezen dat het overspande oppervlakte per tijdseenheid inderdaad constant is. Dit is de tweede wet van Kepler!
De eerste wet van Kepler
Nu de eerste wet. We beginnen met de tweede wet van Newton:
$$ F_{res} = ma $$De enige kracht die op de planeet werkt is de gravitatiekracht. We vinden hiermee:
$$ \frac{GMm}{r^2} = ma $$ $$ \frac{GM}{r^2} = a $$In het hoofdstuk over poolcoördinaten hebben we gezien dat we de versnelling kunnen schrijven als:
$$ a = \ddot{r} - r\dot{\theta}^2 $$De bovenstaande formule wordt:
$$ \frac{GM}{r^2} = \ddot{r} - r\dot{\theta}^2 $$Nu gaan we hier de formule voor het draaimoment aan toevoegen. Er geldt:
$$ L = m(\vec{v} \times \vec{r}) $$In poolcoördinaten wordt dit:
$$ L= mr^2\dot{\theta} $$Als we dit toevoegen aan de bovenstaande formule, dan vinden we:
$$ \frac{GM}{r^2} = \ddot{r} - \frac{L^2}{mr^3} $$Je kan zien dat dit klopt door de formule voor L hierboven in te vullen. We hebben nu een formule die alleen afhankelijk is van r. Als we r oplossen, dan vinden we (na een heftige berekening):
$$ r = \frac{L^2/GMm^2}{(1+e\cos{\theta})} $$ $$ e = \sqrt{1+\frac{2EL^2}{m^3G^2M^2}} $$De e in de formule is een constante die we de ellipticiteit noemen. Als je deze formule uittekent voor verschillende waarde van e, dan vind je:
| e = 0 | Cirkelbaan |
| 0 ≤ e < 1 | Ellipsbaan |
| e = 1 | Paraboolbaan |
| e > 1 | Hyperbolische baan |
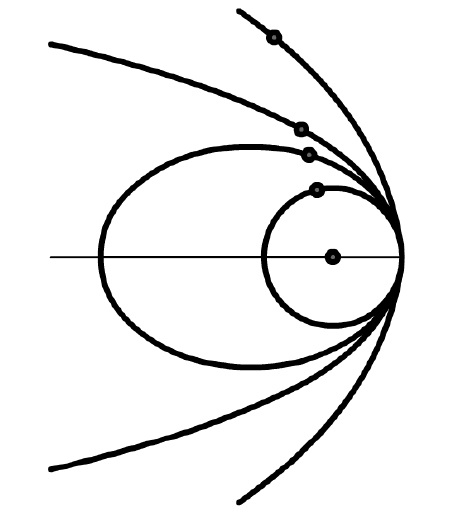
Al deze banen komen we in de ruimte tegen. Voor de planeten zit de waarde netjes tussen 0 en 1 en daarom gaan de planeten in ellipsbanen om de zon! Dit is de eerste wet van Kepler.
De derde wet van Kepler
Een algemene wiskundige formule voor een ellipsbaan is:
$$ r = \frac{b^2/a}{1+e\cos{\theta}} $$a is hier de langste straal van de ellips en b is de kortste straal. Als we dit vergelijken met de formule voor de ellipsbanen die we in het vorige stukje gevonden hadden, dan vinden we:
$$ \frac{L^2}{GMm^2} = \frac{b^2}{a} $$Dit kunnen we herschrijven tot:
$$ L = \sqrt{\frac{GMm^2 b^2}{a}} $$Nu voegen we hier de tweede wet aan toe:
$$ \frac{dA}{dt} = \frac{L}{2m} $$Als we voor Δt de omlooptijd T nemen, dan wordt A de oppervlak van de hele ellips. Dit oppervlak is gelijk aan:
$$ A_{ellips} = \pi ab $$Als we dit invullen en omschrijven, dan vinden we:
$$ L = \frac{2\pi abm}{T} $$Als we de twee formules voor L combineren, dan vinden we:
$$ \frac{2\pi abm}{T} = \sqrt{\frac{GMm^2 b^2}{a}} $$Beide kanten kwadrateren levert:
$$ \frac{4\pi^2 a^2b^2m^2}{T^2} = \frac{GMm^2 b^2}{a} $$Dit kunnen we herschrijven tot:
$$ \frac{T^2}{a^3} = \frac{4\pi^2}{GM} $$Dit is de derde wet van Kepler! Newton vond hiermee niet alleen dat T2/a3 constant was, maar ook dat deze constante afhankelijk was van de massa van de zon! Newton kon met deze ontdekkingen alle bewegingen van de hemellichamen die tot dan toe geobserveerd waren begrijpen! Een van de grootste prestaties van de mensheid!