Met behulp van de wetten van Newton kunnen we een aantal grootheden vinden die constant blijven in de tijd. We noemen dit behouden grootheden. Het bekendste voorbeeld hiervan is het behoud van energie. In deze paragraaf gaan we de belangrijke behouden grootheden uit de Newtoniaanse mechanica afleiden.
De eerste behouden grootheid kunnen we vinden met behulp van de derde wet van Newton:
$$ F_A = -F_B $$Met de tweede wet van Newton kunnen we dit herschrijven tot:
$$ \dot{p}_A = -\dot{p}_B $$En dit kunnen we weer herschrijven tot:
$$ \dot{p}_A + \dot{p}_B = 0$$ $$ \frac{d}{dt}(p_A+p_B) = 0 $$ $$ \dot{p}_{tot} = 0 $$In de laatste vergelijking zien we dat de afgeleide van de totale impuls nul is. Dit kan alleen waar zijn als de totale impuls constant is. We hebben hiermee dus aangetoond dat de totale impuls een behouden grootheid is. We noemen dit het behoud van impuls.
Laten we deze wet toepassen. Hieronder zien we twee dezelfde deeltjes die botsen en daarna gezamelijk verder bewegen. We noemen dit een inelastische botsing. Bij een elastische botsing bewegen de deeltjes los van elkaar verder. De snelheid van het linker deeltje noemen we u. De snelheid van het deeltje dat tijdens de botsing ontstaat noemen we v.
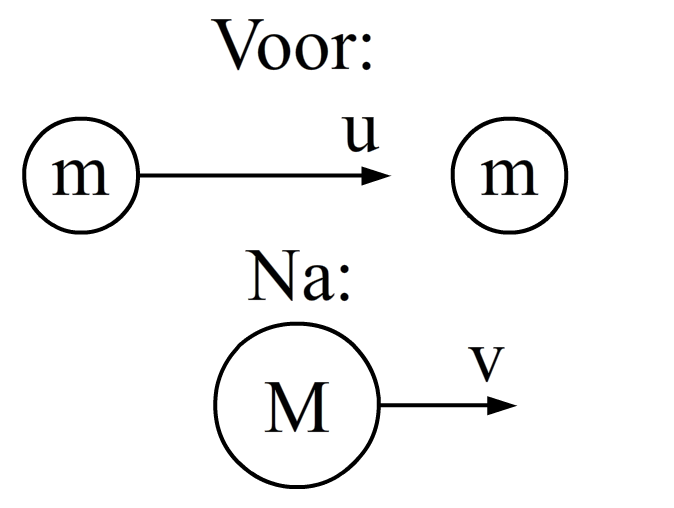
Met impulsbehoud vinden we:
$$ mu + 0 = Mv $$ $$ mu = 2mv $$ $$ u = 2v $$We hebben hier dus geleerd dat de snelheid v van het deeltje dat bij de botsing ontstaat twee keer zo klein als de oorspronkelijke snelheid u.
Nog een voorbeeld. Een deeltje ligt eerst stil en explodeert in twee gelijke delen.

Met behoud van impuls vinden we:
$$ 0 = mv_1 + mv_2 $$ $$ v_1 = -v_2 $$Aan deze formule kunnen we zien dat beide delen met dezelfde snelheid, maar in tegengestelde richting bewegen.
Voor een tweede behoudswet definiëren we eerst het zogenaamde moment (M):
$$ \vec{M} = \vec{r} \times \vec{F} $$r is hier wederom de radiusvector en F is de kracht die op het voorwerp werkt. Het kruisje staat hier voor het kruisproduct. De definitie hiervan is:
$$ \vec{A} \times \vec{B} = AB\sin{\theta} $$De hoek θ is hier de hoek tussen de richting van A en B. Merk op dat als A en B in dezelfde of in tegengestelde richting wijzen, dat de sinus gelijk aan nul wordt en dat hierdoor het hele kruisprodukt nul wordt.
Naast het moment definiëren we ook het impulsmoment (L):
$$ \vec{L} = \vec{r} \times \vec{p} $$Als we de afgeleide van het impulsmoment naar de tijd nemen, dan vinden we met de produktregel dat:
$$ \dot{L} = \frac{d(\vec{r} \times \vec{p} )}{dt} = \vec{v} \times \vec{p} + \vec{r} \times \vec{F} $$Met p=mv en met L = r × p kunnen we dit herschrijven tot:
$$ \dot{L} = m \vec{v} \times \vec{v} + \vec{M} $$De linker term wordt nul, omdat beide vectoren v in dezelfde richting wijzen en als gevolg is de sinus in het kruisproduct nul. We vinden dus:
$$ \dot{L} = \vec{M} $$In situaties waarbij het moment M nul is, vinden we:
$$ \dot{L} = 0 \;\;\;\; \text{(als M = 0)} $$In dit geval is L dus constant en dus een behouden grootheid. Maar in welke gevallen in M nul? Het moment is het kruisprodukt tussen F en r. Als F en r in dezelfde of tegenovergestelde richting wijzen, dan is het moment dus nul (want sin(0)=0 en sin(180)=0). Dit gebeurt bijvoorbeeld bij voorwerpen die in een cirkelbaan bewegen. Neem bijvoorbeeld een planeet die om de zon beweegt. De radiusvector wijst van de zon naar de planeet en de kracht wijst van de planeet naar de zon. r en F wijzen hier dus in tegenovergestelde richting en M wordt hierdoor dus nul.
Wat kunnen we hiermee? Als L constant is, dan weten we dat r × mv constant is. Stel dat een planeet in een ellipsbaan om de zon beweegt, dan zal de r in de tijd veranderen. Als de r kleiner wordt, dan moet volgens het behoud van impulsmoment de snelheid groter worden. Dit is precies wat we zien. Ditzelfde effect heb je bijvoorbeeld ook als je een steen aan een touw rondslingert en dan de steen meer naar je toe trekt. De snelheid van de steen zal toenemen.
Als laatste bespreken we behoud van energie. We moeten hiervoor eerst de arbeid definiëren:
$$ W = \int F dx $$Gebruikmakend van \(dx = v dt\) en \(F=ma=m\dot{v}\), vinden we:
$$ W = m \int \dot{v} v dt $$Met de productregel zien we dat geldt dat:
$$ \frac{1}{2}\frac{dv^2}{dt} = \frac{1}{2}(v\dot{v} + \dot{v}v) = \dot{v}v $$Als we dit in de bovenstaande formule stoppen, dan vinden we:
$$ W = \frac{1}{2} m \int \frac{dv^2}{dt}dt = \frac{1}{2}m \int dv^2 $$Als we de integraal uitwerken vinden we:
$$ W = \frac{1}{2}mv_b^2 - \frac{1}{2}mv_e^2$$ $$ W = \Delta E_{kin}$$Deze formule wordt het arbeid-energietheorema genoemd.
Laten we deze formule eens toepassen, bijvoorbeeld op het vallen van een bal van hoogte hb naar hoogte he. Voor de arbeid vinden de dan:
$$ W = \int_{h_b}^{h_e} F_z dh = mg \int_{h_b}^{h_e} dh = mgh_b - mgh_e $$Het arbeid-energietheorema wordt dan:
$$ mgh_b - mgh_e = \frac{1}{2} mv_e^2 - \frac{1}{2} mv_b^2 $$Dit kunnen we herschrijven tot:
$$ mgh_b + \frac{1}{2} mv_b^2 = mgh_e + \frac{1}{2} mv_e^2 $$We zien hier dat de zwaarte-energie en de kinetische energie tezamen aan het begin en het eind van de beweging gelijk zijn. Er geldt dus:
$$ E_z + E_{kin} = \text{constant} $$In dit specifieke geval hebben we dus energiebehoud aangetoond. We kunnen energiebehoud echter nog algemener bewijzen. We bestuderen hiervoor een willekeurige kracht van de vorm F(x). De bijbehorende energie noemen we de potentiële energie. We gaan nu laten zien dat de potentiële energie behouden is als deze wordt gegeven door:
$$ F(x) = -\frac{dE_{pot}(x)}{dx} $$Bij de zwaartekracht hoort bijvoorbeeld de potentiële energie gelijk aan Ez = mgh:
$$ F_z = -\frac{d(mgh)}{dh} = -mg $$De volgende stap is om te bewijzen dat voor al deze soorten potentiële energie energiebehoud geldt. Als we de formule voor F(x) invullen in de formule voor de arbeid, dan vinden we:
$$ W = \int F(x) dx = -\int \frac{dE_{pot}(x)}{dx} dx = E_{pot,b}(x) - E_{pot,e}(x) $$Met het arbeid-energietheorema wordt dit:
$$ E_{pot,b} - E_{pot,e} = E_{kin,e} - E_{kin,b} $$Dit kunnen we herschrijven tot:
$$ E_{kin,b} + E_{pot,b} = E_{kin,e} + E_{pot,e} $$Er geldt dus:
$$ E_{tot} = E_{kin} + E_{pot} = \text{constant}$$Training
-
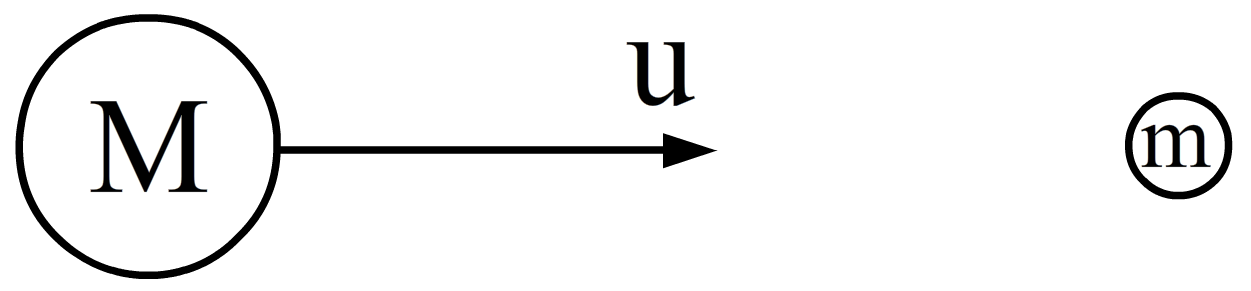
In de volgende afbeelding zien we twee deeltjes. Het linker deeltje heeft een grote massa M en beweegt met snelheid u en het rechter deeltje heeft een verwaarloosbare massa m en staat stil. De botsing is inelastisch. Ga na wat er met beide deeltjes gebeurt na de botsing.
-
In de volgende afbeelding zien we twee deeltjes. Het linker deeltje heeft een verwaarloos kleine massa m en beweegt met snelheid u en het rechter deeltje heeft een grote massa M en staat stil. De botsing is inelastisch. Ga na wat er met beide deeltjes gebeurt na de botsing.

-
Een massa M valt uitelkaar in twee gelijke delen met massa m. Ga na wat er met beide deeltjes gebeurt na de botsing.

-
In de volgende afbeelding zien we twee deeltjes met dezelfde massa. Het linker deeltje beweegt met snelheid u en het rechter deeltje staat stil. De botsing is elastisch. Ga na wat er met beide deeltjes gebeurt na de botsing. Gebruik hiervoor zowel de wet van impulsbehoud als de wet van energiebehoud.

-
- Een kunstschaatser draait met uitgestrekte been en armen een rondje om zijn eigen as. Dan trekt de persoon zijn been en armen in. Leg met behulp van het behoud van impulsmoment uit wat er gebeurt met de schaatser.
- De planeet Pluto beweegt in een ellipsbaan om de zon. Leg met behulp van het behoud van impulsmoment uit wat er met de snelheid van pluto gebeurt als de planeet dichter bij de zon komt.
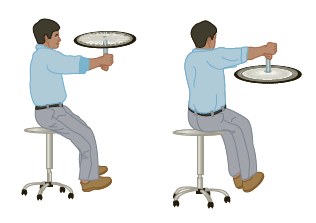
- Een persoon houdt een draaiend wiel horizontaal in zijn handen (zie de afbeelding). De persoon gaat zitten op een bureaustoel die kan draaien. Dan draait de persoon het wiel 180 graden om. Leg met behulp van het behoud van impulsmoment uit wat er dan gebeurt met de persoon.
- Een wiel wordt aan een touw gehangen zoals in de onderstaande afbeelding te zien is.
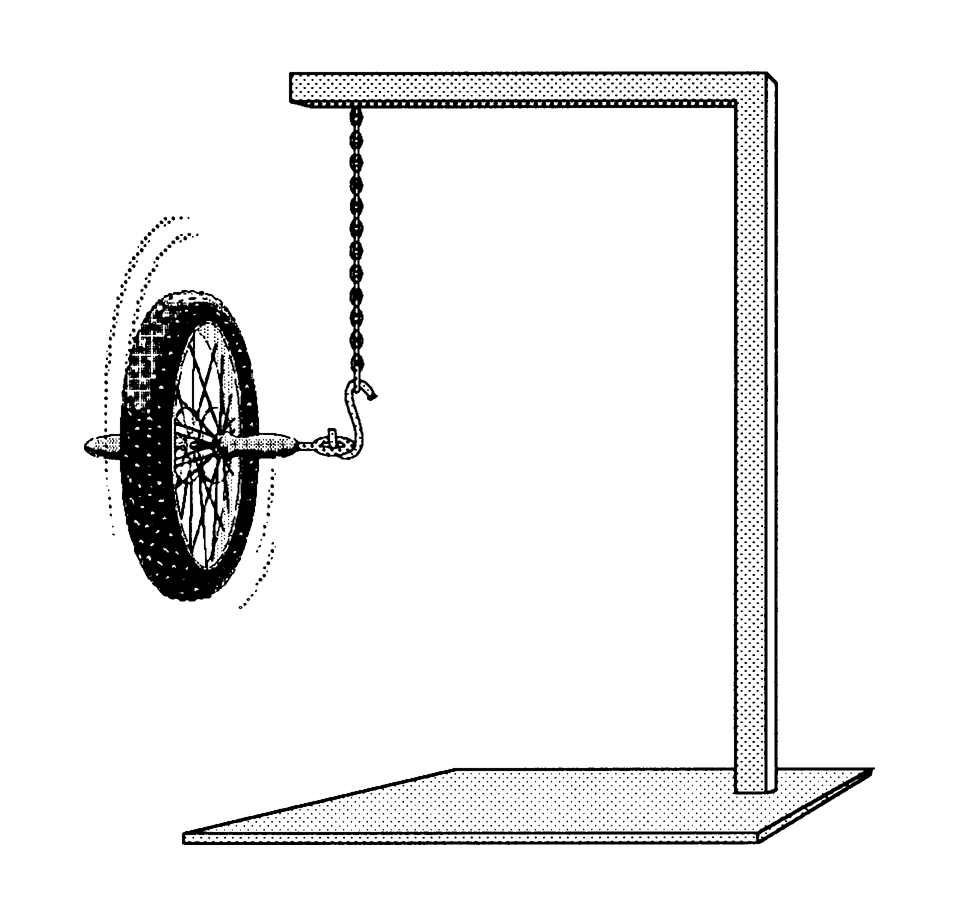
- Leg uit wat er met het wiel gebeurt als deze wordt losgelaten als het wiel niet draait.
-
Leg uit wat er met het wiel gebeurt als deze wordt losgelaten als het wiel snel draait. Gebruik hierbij de volgende afbeelding. We zien hier een wiel van de bovenkant gezien.
Teken de snelheid die de bovenkant van het wiel in de bovenstaande afbeelding zal krijgen bij het loslaten.