In het hoofdstuk over kwantummechanica stelden we deeltjes voor als golffuncties die veranderen in de tijd. Het kwadraat van deze golffunctie gaf ons de kans om een deeltje op een bepaalde locatie of met een bepaalde snelheid aan te treffen. Richard Feynman, een van de belangrijkste wetenschappers van de 20ste eeuw, ontdekte een nieuwe versie van de kwantummechanica. Hij gebruikte in plaats van een golffunctie een som van alle mogelijke paden die het deeltje kan nemen tussen twee punten. Hij maakte hierbij gebruik van de Lagrangiaanse mechanica.
Zijn nieuwe methode begon met een simpel gedachten experiment. Als een elektron door een dubbele spleet gaat, dan hangt de kans dat het elektron op een bepaalde plek komt af van de inteferentie van een golf die door de ene spleet is gegaan met een golf die door de andere speel is gegaan. De waarde van elke golf wordt de amplitude van de golf genoemd en als we deze amplitude optellen en het kwadraat nemen, dan krijgen we de kans dat het deeltje op die bepaalde plek terecht zal komen.
De volgende stap van Feynman was om een scherm voor de stellen met niet twee speleten, maar oneindig spleten. In dat geval gaat de golf door al deze spleten. Het neemt dus al deze mogelijke paden. Het scherm zit dan echter zo vol gaten dat er eigenlijk niet meer van een scherm te spreken valt. Neemt een deeltje zonder scherm dan niet ook alle mogelijke paden? We gaan in deze paragraaf zien dat dit inderdaad klopt.
We kunnen dit beeld nog extremer maken door niet één scherm te nemen, maar een hele serie schermen (wellicht oneindig) die we achter elkaar zetten, met elk oneindig gaten. Er zijn nu paden mogelijk waarbij het deeltje in zigzagbewegingen op het scherm komt. Als het deeltje van A naar B gaat neemt het dus alle denkbare paden! Dit klinkt absurd, maar zo blijkt het toch te werken. De bekende natuurkundige Freeman Dyson schreef hierover:
Eenendertig jaar geleden vertelde Richard Feynman mij over zijn 'som over alle paden'-versie van de kwantummechanica. 'Het elektron doet alles waar het zin in heeft', zei hij. 'Het gaat in elke richting, met elke snelheid, voorwaarts en achterwaarts in de tijd, waar het ook maar zin in heeft. En wanneer je de amplitudes van de paden bij elkaar optelt, dan krijg je de golffunctie'. Ik zei tegen hem 'je bent gek'. Maar dat was hij niet.
In deze paragraaf gaan we deze alernatieve kwantummechanica bestuderen.
De padintegraal
Voordat we al deze paden gaan bestuderen, hebben we eerst kennis nodig van de zogenaamde time evolution operator. Dit is de operator waarmee we de golffunctie van een tijdstip t = 0 naar een later tijdstip t kunnen transformeren. In wiskundige termen wordt dit:
$$ \Psi(x,t) = \hat{U}(t) \Psi(x,0) $$Het blijkt dat deze U ook voldoet aan de Schrodingervergelijking:
$$ i\hbar \partial_t \hat{U} = \hat{E} \hat{U} $$Dit weten we omdat als we beide kanten laten werken op ψ(x,0), dan vinden we de Schrodingervergelijking terug in zijn gebruikelijke vorm. Als we de bovenstaande vergelijking oplossen, dan vinden we:
$$ \hat{U} = e^{-i\hat{E}t} $$De formule waarmee we begonnen wordt dus:
$$ \Psi(x,t) = e^{-i\hat{E}t} \Psi(x,0) $$We beginnen nu met de volgende formule:
$$ \Psi(x_n,t_n) = \int \delta(x - x_n) \Psi(x,t_n) $$In de vorige paragraaf hebben we gezien dat de delta-functie gelijk is aan de golffunctie van een golf waarvan de positie bekend is. We kunnen dus ook schrijven dat:
$$ \Psi(x_n,t_n) = \int \psi(x_n) \Psi(x,t_n) $$Met de tijd evolutie operator kunnen we dit schrijven als:
$$ \Psi(x_n,t_n) = \int \psi(x_n) e^{i\hat{E}t }\psi(x) $$We kunnen voor het gemag de tijd evolutie operator ook even toevoegen aan ψ(xn). We schrijven dan:
$$ \Psi(x_n,t_n) = \int \psi(x_n,t_n) \psi(x) $$In Dirac-notatie wordt dit:
$$ \Psi(x_n,t_n) = \langle \psi(x_n,t_n) | \psi(x) \rangle $$We gaan nu aan deze vergelijking de identieitsoperator toevoegen. Deze operator wordt gegeven door:
$$ 1 = \int dx_0 | \psi(x_0,t_0) \rangle \langle \psi(x_0,t_0) | $$We vinden:
$$ \Psi(x_n,t_n) = \int dx_0 \langle \psi(x_n,t_n) | \psi(x_0,t_0) \rangle \langle \psi(x_0,t_0) | \psi(x) \rangle $$Dit kunnen we versimpelen tot:
$$ \Psi(x_n,t_n) = \int dx_0 \langle \psi(x_n,t_n) | \psi(x_0,t_0) \rangle \psi(x_0,t_0) $$De Dirac-term in de integraal noemen we de propagator. Het geeft ons de amplitude dat een deeltje van x0 naar xn beweegt van tijdstip t0 tot tn. Deze propagator gaan we hieronder uitwerken.
We voegen eerst weer een identiteitsoperator toe:
$$ \langle \psi(x_n,t_n) | \psi(x_0,t_0) \rangle = \int dx_1 \langle \psi(x_n,t_n) | \psi(x_1,t_1) \rangle\langle \psi(x_1,t_1) | \psi(x_0,t_0) \rangle $$We zien hier dat de amplitude om van het x0 naar xn te gaan gelijk is aan de amplitude om eerst van x0 op tijdstip t0 naar x1 op tijdstip t1 te gaan en dan naar xn op tijdstip tn. We moeten zoals je ziet in sommeren (integreren) over alle mogelijke posities x1. In de volgende afbeelding zien we hier een schematische afbeelding van.
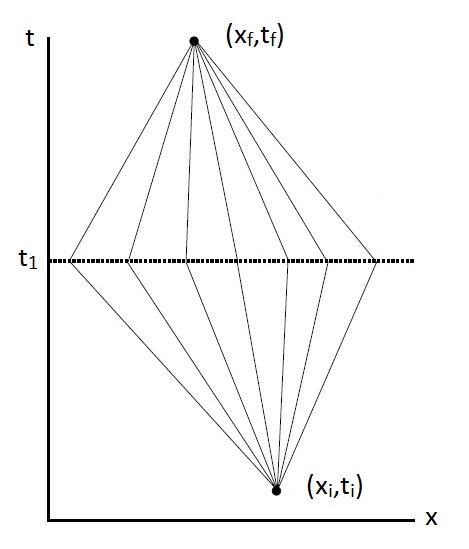
We kunnen identiteitsoperatoren blijven toevoegen totdat we de propagator hebben opgedeeld in stapjes Δt:
$$ \langle \psi(x_n,t_n) | \psi(x_0,t_0) \rangle = \int dx_1...dx_{n-1} \langle \psi(x_n,t_n) | \psi(x_{n-1},t_{n-1}) \rangle ... \langle \psi(x_2,t_2) | \psi(x_1,t_1) \rangle \langle \psi(x_1,t_1) | \psi(x_0,t_0) \rangle $$In de onderstaande afbeelding zien we dat bij het toenemen van het aantal stapjes, dat we uiteindelijk alle mogelijk paden uitrekenen.
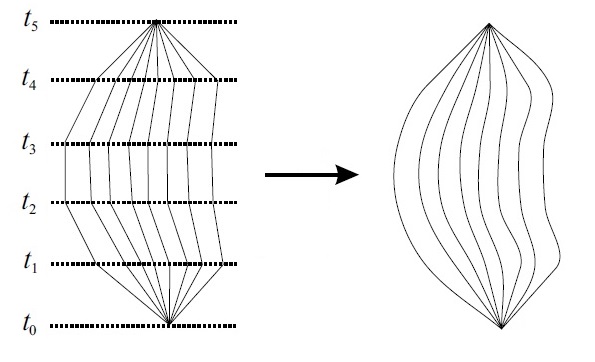
We gaan nu naar één stukje kijken uit de bovenstaande integraal. Zo'n stukje heeft in het algemeen de vorm:
$$ \langle \psi(x_{j+1},t_{j+1}) | \psi(x_j,t_j) \rangle = \langle \psi(x_{j+1}) | e^{-i\hat{E}t_{j+1} } e^{i\hat{E}t_j} | \psi(x_j) \rangle = \langle \psi(x_{j+1}) | e^{-i\hat{E}\Delta t} | \psi(x_j) \rangle $$De e-macht in de integraal kunnen we als volgt benaderen:
$$ e^{ix} = 1 + ix + ... $$ $$ e^{-iE\Delta t} = 1 - i\Delta t \hat{E} + ... $$ $$ e^{-iE\Delta t} = 1 - \frac{i\Delta t}{2m} (\hat{p}^2) - i\Delta t V(\hat{x}) + ... $$De bovenstaande formule wordt hiermee:
$$ \langle \psi(x_{j+1},t_{j+1}) | \psi(x_j,t_j) \rangle = \langle \psi(x_{j+1}) | \psi(x_j) \rangle - \frac{i\Delta t}{2m} \langle \psi(x_{j+1}) |\hat{p}^2| \psi(x_j) \rangle - i\Delta t \langle \psi(x_{j+1}) |V(\hat{x})| \psi(x_j) \rangle$$Laten we alle termen één voor één uitwerken. De eerste term kunnen we, zoals we in de vorige paragraaf gezien hebben, schrijven als:
$$ \langle \psi(x_{j+1}) | \psi(x_j) \rangle = \delta(x_{j+1} - x_j) = \frac{1}{2\pi} \int dp e^{ip(x_{j+1}-x_j) }$$De tweede term kunnen we met behulp van identiteitsoperatoren schrijven als:
$$ \langle \psi(x_{j+1}) |\hat{p}^2| \psi(x_j) \rangle = \int dp' dp \langle \psi(x_{j+1}) | \psi(p' ) \rangle \langle \psi(p' ) |\hat{p}^2| \psi(p) \rangle \langle \psi(p) | \psi(x_{j}) \rangle$$De extra indentiteitsoperatoren zorgen er nu voor dat de operator p omgezet kan worden in een eigenwaarde p. We zien hier namelijk dat de operator p werkt op de eigenfunctie voor een specifieke p. Zoals we in de vorige paragraaf hebben gelezen krijgen we dan de eigenwaarde p terug.
$$ \hat{p}^2 | \psi(p) \rangle = p^2 | \psi(p) \rangle $$Omdat p nu gewoon een getal is, kunnen we het uit het inprodukt halen. We vinden dus:
$$ \langle \psi(x_{j+1}) |\hat{p}^2| \psi(x_j) \rangle = \int dp' dp p^2\langle \psi(x_{j+1}) | \psi(p' ) \rangle \langle \psi(p' ) | \psi(p) \rangle \langle \psi(p) | \psi(x_{j}) \rangle$$Deze integraal kunnen we uitwerken met:
$$ \langle \psi(x_{j+1}) | \psi(p') \rangle = \frac{1}{\sqrt{2\pi}} \int dx e^{ip'x}\delta(x-x_{j+1}) = \frac{1}{\sqrt{2\pi}} e^{ip'x_{j+1}} $$ $$ \langle \psi(p) | \psi(x_{j}) \rangle = \frac{1}{\sqrt{2\pi}} \int dx e^{-ipx}\delta(x-x_j) = \frac{1}{\sqrt{2\pi}} e^{-ipx_j} $$ $$ \langle \psi(p') | \psi(p) \rangle = \frac{1}{2\pi} \int dx e^{i(p-p')x} = \delta(p'-p) $$We vinden nu:
$$ \langle \psi(x_{j+1}) |p^2| \psi(x_j) \rangle = \frac{1}{2\pi} \int dp'dp e^{ip' x_{j+1}} e^{-ip x_{j}} p^2 \delta(p'-p) = \frac{1}{2\pi} \int dp e^{ip (x_{j+1} - x_{j})} p ^2 $$Als laatste hadden we nog de term met de potentiële energie V. Hier werkt de operator x op de eigenfunctie voor een specifieke x. Als gevolg krijgen we de eigenwaarde x. We vinden:
$$ V(\hat{x}) | \psi(x_j) \rangle = V(x_j) \delta(x-x_j) $$Ook V kunnen we nu dus buiten het inprodukt plaatsen.
Als we dit allemaal samenvoegen vinden we:
$$ \langle \psi(x_{j+1}) | \psi(x_j) \rangle = \frac{1}{2\pi} \int dp e^{ip (x_{j+1}-x_j)} - \frac{i\Delta t}{2m} \int dp e^{ip (x_{j+1}-x_j)}p^2 - i\Delta t \frac{1}{2\pi} \int dp e^{ip(x_{j+1}-x_j)}V(x_j) $$Dit kunnen we simpeler schrijven als:
$$ \langle \psi(x_{j+1}) | \psi(x_j) \rangle = \frac{1}{2\pi} \int dp e^{i(p\Delta x - E \Delta t )} $$We zien hier dat voor elk tijdstapje wordt geintegreert over alle mogelijke waarde van de impuls. Dit is dus ook een som over alle mogelijke snelheden.
Merk op dat we nu helemaal geen operatoren meer in onze uitspraak hebben. Dit is een van de voordelen van Feynman's kwantummechanica. We hebben geen golffunctie en geen operatoren. We hebben alleen paden.
De term in de macht die tussen haken staat kunnen we als volgt omschrijven:
$$ p \Delta x - H \Delta t = \left( p \frac{\Delta x}{\Delta t} - H \right) \Delta t = ( 2E_{kin} - (E_{kin} + E_{pot})) \Delta t = ( E_{kin} - E_{pot}) \Delta t = L\Delta t $$We volledige integraal voor één tijdstapje wordt dus:
$$ \langle x_{j+1} | e^{-iH\Delta t} | x_j \rangle = \frac{1}{2\pi}\int dp e^{iL \Delta t} $$Als we de integraal oplossen, dan vinden we:
$$ \langle x_{j+1}| e^{-iH\Delta t} | x_j \rangle = \left( \frac{m}{2\pi i \tau}\right)^{1/2} e^{iL\Delta t} $$Als we nu de N stapjes samenvoegen, dan vinden we:
$$ \langle x_n, t_n| x_0,t_0 \rangle = \left(\frac{m}{2\pi i \tau}\right)^{n/2} \int \Pi_{i=0}^{n-1} dx_i e^{ i \Sigma_{j=0}^{n-1} \tau L \Delta t} $$De Π staat hier voor een vermenigvuldiging van de verschillende dxi. Als we nu de limiet nemen naar Δ t is nul, dan vinden we:
$$ \langle x_n, t_n| x_0,t_0 \rangle = \lim_{n\rightarrow \infty }\left(\frac{m}{2\pi i \tau}\right)^{n/2} \int \Pi_{i=0}^{n-1} dx_i e^ {i \int_{t_0}^{t_n} L dt} $$De integraal in de e-macht is echter gelijk aan de actie. We kunnen dus ook schrijven:
$$ \langle x_n, t_n| x_0,t_0 \rangle = \lim_{n\rightarrow \infty }\left(\frac{m}{2\pi i \tau}\right)^{n/2} \int \Pi_{i=0}^{n-1} dx_i e^ {iS} $$Dit korten we meestal af tot:
$$ \langle x_n, t_n| x_0,t_0 \rangle = \int Dx e^{iS/\hbar} $$Dit is uiteindelijk de belangrijkste formule uit deze paragraaf. In D zit verscholen een integraal over alle paden van punt x0 naar xn en elk pad voegt een factor eiS/ℏ toe.
Voordat we deze formule gaan interpreteren is het van belang dat we eerst even begrijpen wat een factor van deze vorm eigenlijk voorstelt. Hieronder zien we een grafiek van de formule eix. Zoals je ziet kan je deze factor voorstellen als een vector die roteert in de imaginaire ruimte. De vector heeft telkens dezelfde lengte. We noemen dit ook wel de fase.
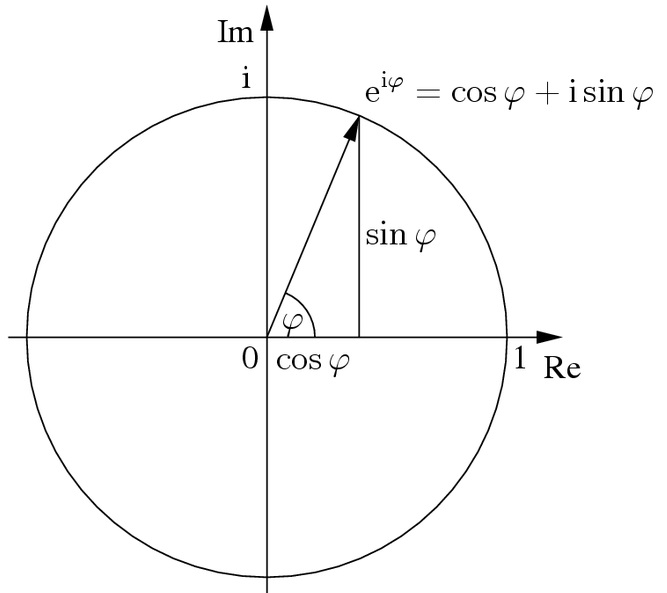
Elk pad eiS/ℏ draagt dus een vector bij aan de totale amplitude. Het kwadraat van deze totale vector is dan de kans dat een deel het bepaalde pad zal volgen.
Omdat er oneindig mogelijke paden zijn, lijkt dit onmogelijk om uit te rekenen. Gelukkig heffen de effecten van de meeste paden elkaar op. Dit komt door de constante van Planck in de e-macht. Deze constante is zo klein, dat een kleine verandering in de actie meteen zorgt dat de vector meteen vele rotaties gemaakt heeft en dus in een willekeurige richting komt te staan. Als nabijgelegen paden dus een verschillende actie hebben, dan zullen al deze paden elkaar opheffen.
Alleen op plekken waar de actie bij nabijgelegen paden zo goed als gelijk is, zullen we vectoren constructief optellen. Dit gebeurt op plekken waar de actie minimaal is. Op het minimum van een functie is de helling namelijk even nul en rond dit punt is de actie dus constant. Dit verklaart waarom klassieke deeltjes altijd het pad nemen waar de actie minimaal is. Eigenlijk word door deze deeltjes elk mogelijk pad genomen, met elk een amplitude eiS/ℏ, maar overal heffen deze amplitudes elkaar op behalve bij het pad waar de actie minimaal is!
De Schrödingervergelijking
Met de padintegraalmethode kunnen we ook de Schrödingervergelijking afleiden. We beginnen hier met de padintegraal waarbij we de actie integreren langs een oneindig klein tijdstapje ε. De N wordt in dat geval gelijk aan 1 en we vinden dus:
$$ \psi(x,t+\epsilon) = \sqrt{\frac{m}{2i\pi \hbar \epsilon}} \int_{-\infty}^{\infty} \exp{\frac{i}{\hbar} S } \psi(x,t) $$In het oneindig kleine tijdstapje wordt de actie gelijk aan Lε. We vinden:
$$ \psi(x,t+\epsilon) = \sqrt{\frac{m}{2i\pi \hbar \epsilon}} \int_{-\infty}^{\infty} \exp{\frac{i\epsilon}{\hbar} \left( \frac{1}{2}m\left( \frac{x-y}{\epsilon} \right)^2 - V\left(\frac{x+y}{2},t+\frac{\epsilon}{2} \right) \right) } \psi(y,t) $$We hebben hier gebruikt dat Δx = x - y en we hebben de gemiddelde poteniële energie genomen betreft in zowel de positie als de tijd. Als we deze integraal oplossen, dan vinden we:
$$ \psi(x,t+\epsilon) = \left( 1-\frac{i\epsilon}{\hbar}V \right) \psi(x,t) + \frac{i\hbar \epsilon}{2m} \left[ \left( 1-\frac{i\epsilon}{\hbar}V \right) \frac{\partial^2 \psi(x,t)}{\partial x^2} - \frac{i\epsilon}{\hbar} \frac{\partial V}{\partial x}\frac{\partial \psi(x,t)}{\partial x} \right] $$De linker termn kunnen we uitwerken met de Taylorbenadering. We vinden dan:
$$ \psi(x,t+\epsilon) = \psi(x,t) + \epsilon \frac{\partial \psi(x,t)}{\partial t} + ... $$Als we dit invullen in de bovenstaande vergelijking, dan vinden we:
$$ \psi(x,t) + \epsilon \frac{\partial \psi(x,t)}{\partial t} = \left( 1-\frac{i\epsilon}{\hbar}V \right) \psi(x,t) + \frac{i\hbar \epsilon}{2m} \left[ \left( 1-\frac{i\epsilon}{\hbar}V \right) \frac{\partial^2 \psi(x,t)}{\partial x^2} - \frac{i\epsilon}{\hbar} \frac{\partial V}{\partial x}\frac{\partial \psi(x,t)}{\partial x} \right] $$Aan beide kanten kunnen we ψ wegstrepen. Als we dan ook beide kanten delen door ε, dan vinden we:
$$ \frac{\partial \psi}{\partial t} = -\frac{i}{\hbar}V \psi + \frac{i\hbar}{2m} \left[ \left( 1-\frac{i\epsilon}{\hbar}V \right) \frac{\partial^2 \psi}{\partial x^2} - \frac{i\epsilon}{\hbar} \frac{\partial V}{\partial x}\frac{\partial \psi}{\partial x} \right] $$Als we nu de limiet nemen waarbij ε naar nul gaat, dan vinden we:
$$ \frac{\partial \psi}{\partial t} = -\frac{i}{\hbar}V \psi + \frac{i\hbar}{2m} \frac{\partial^2 \psi}{\partial x^2} $$En dit is de Schrödingervergelijking.