Als op een voorwerp alleen een middelpuntzoekende kracht werkt, dan geldt volgens de tweede wet van Newton:

$$ F_{mpz} = F_{res} = ma $$

De middelpuntzoekende kracht zorgt dus voor een versnelling. Maar hadden we niet aangenomen dat de baansnelheid constant is? Toch is er sprake van een versnelling. Dit kunnen we goed zien in de onderstaande afbeelding. Een versnelling richting het midden van de cirkelbaan zorgt ervoor dat het voorwerp in zijn cirkelbaan blijft. Het gevolg van de versnelling is dat de snelheid van richting verandert.

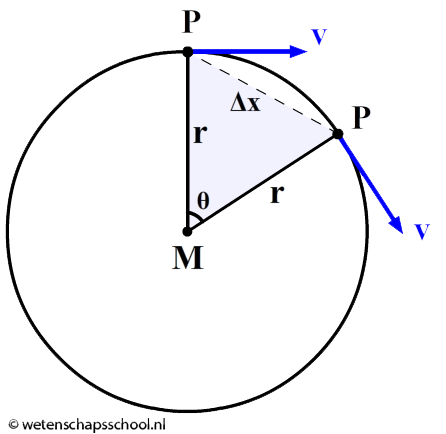
In de onderstaande afbeelding beschrijven we dezelfde beweging, maar dan gezien vanaf het punt P zelf. Wederom is duidelijk dat de snelheidsvector gedurende de beweging van richting veranderd is. Zoals gebruikelijk noemen we het verschil tussen deze snelheden Δv.

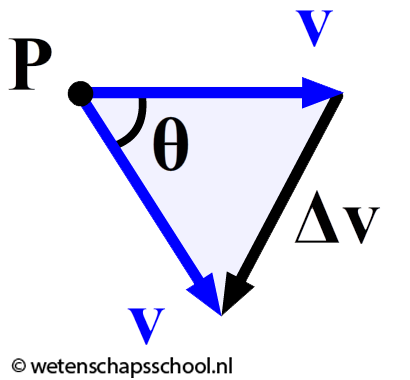
In de vorige twee afbeeldingen zien we twee gelijkbenige driehoeken met dezelfde hoek θ. Deze twee driehoeken hebben dus dezelfde verhoudingen. Er geldt dus:

$$ \frac{\Delta x}{r} = \frac{\Delta v}{v} $$

Dit kunnen we omschrijven tot:

$$ \Delta v = \frac{v \Delta x}{r} $$

Als we beide zijden door \( \Delta t \) delen, dan vinden we:

$$ \frac{\Delta v}{\Delta t} = \frac{v \frac{\Delta x}{\Delta t}}{r}$$

Omdat \( a = \Delta v / \Delta t \) en \( v = \Delta x / \Delta t \), vinden we:

$$ a_{mpz} = \frac{v_{baan}^2}{r}$$

Dit is de grootte van de middelpuntzoekende versnelling. Deze formule is voor het eerst afgeleid door de nederlandse natuurkundige Christiaan Huygens.

Met de formule voor de versnelling kunnen we ook gemakkelijk de formule voor de middelpuntzoekende kracht afleiden:

$$ F_{mpz} = ma_{mpz} = m\frac{v^2}{r} $$

Met deze formule voor de middelpuntzoekende versnelling kunnen we bijvoorbeeld de versnelling van de maan uitrekenen. De maan heeft een omlooptijd van 27,32 dagen (2,36 × 10⁶ s) en de afstand van het centrum van de aarde tot het centrum van de maan is 3,85 × 10⁸ m. De baansnelheid is dus gelijk aan:

$$ v_{baan} = \frac{2\pi r}{T} = \frac{2\pi \times 3,85\times 10^8}{2,36\times 10^6} = 1,03 \times 10^3 \text{ m/s} $$

Met de baansnelheid kunnen we de versnelling uitrekenen:

$$ a_{mpz} = \frac{v_{baan}^2}{r} = \frac{(1,03 \times 10^3)^2}{3,85\times 10^8} = 0,00273 \text{ m/s}^2 $$

Dit is de valversnelling die de maan ondergaat! Vanwege de grote afstand van de aarde is dit een stuk kleiner dan de 9,81 m/s² die we op aarde gewend zijn (zie de onderstaande afbeelding)! De valversnelling is over deze afstand dus een factor 9,81/0,00273 ≈ 3600 afgenomen.

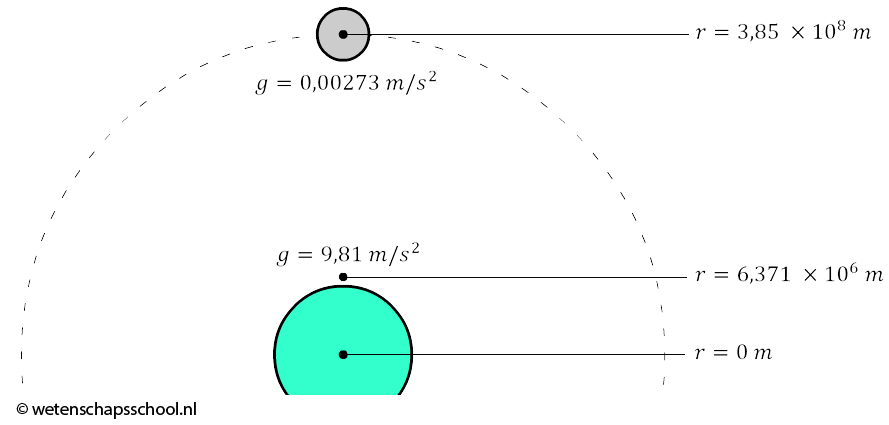
Newton deed voor het eerst onderzoek naar dit verschil. Newton wist dat de afstand van de aarde tot de maan 60x zo groot was als de straal van de aarde. Over deze afstand was de valversnelling 60² = 3600x afgenomen. We hebben hier dus te maken met een omgekeerd kwadratisch verband. Er geldt dus:

$$ g = \frac{\text{constant}}{r^2} $$

De gravitatiekracht op een voorwerp wordt dan:

$$ F_g = \frac{\text{constant} \times m}{r^2} $$

Volgens de derde wet van Newton oefent het voorwerp een even grote kracht uit op de aarde (zie de onderstaande afbeelding). Er geldt dus ook:

$$ F_g = \frac{\text{constant} \times M}{r^2} $$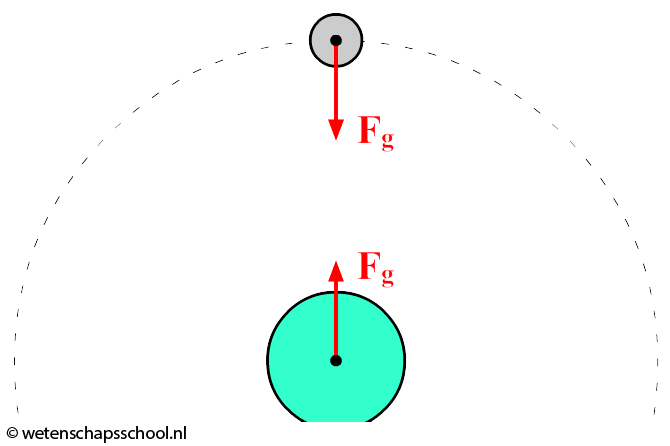

Als we deze formules combineren, dan vinden we:

$$ F_g = \frac{\text{constant} \times Mm}{r^2} $$

De constante wordt nu G genoemd en dit geeft ons de bekende formule voor de gravitatiekracht:

$$ F_g = \frac{\text{GMm}}{r^2} $$